基于G1-CRITIC-云物元法的风电集群有功控制策略综合评价

孙佳航，黄景光，冯忠楠，李浙栋，李振兴

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.华中科技大学强电磁工程与新技术国家重点实验室，湖北武汉 430074）

0 引言

在碳达峰、碳中和奋斗目标的指引下，风电具备极大的发展潜能，截至2020 年6 月底，我国风电累计装机达到2.92 亿千瓦，预计到2025 年达到3.78 亿千瓦[1]，但其本身具有的随机性、波动性、难预测性对电网造成的冲击也逐渐突显，对风电集群进行统一调度和协调控制可有效缓解风电不确定性引发的电力系统扰动问题，使集群在外部特性上接近常规机组，制定合理的风电集群有功控制策略可在保证电网安全稳定运行的基础上充分利用风能资源提高经济效益。目前已有不少风电集群有功控制策略的研究成果[1-4]，但都基于特定的目标进行策略的优化调整，较少关注各方面效益的重要性考量及其综合性能评估，而集群有功控制方案的选择及策略的制定需充分协调各方面经济及技术效益，因此，有必要对风电集群有功控制策略进行综合评价。

对风电集群有功控制效果进行多角度的指标定量分析利于提高综合评价结果的合理性，目前的研究较少。文献[5]提出集群输出波动指数、集群偏差度等指标反映风电集群有功控制效果。文献[6]针对风电集群出力相关性与互补性构建指标体系。有功控制旨在对风电接入电网的调峰、调频及调压效果起到正反馈作用[7]，因而用于评价风电并网在调峰、调频及调压方面效益的指标[8-10]对风电集群有功控制效果具有表征作用。综合评价方法的研究中，文献[11-14]分别采用德尔菲法、数据包络法、层次分析法、贝叶斯法实现综合性能的评估，但都未能刻画评价过程的随机性与不确定性。本文从安全稳定性、经济性、利用水平3 个方面构建评价指标体系，采用G1-CRITIC（Criteria Importance Through Intercrieria Correlation）法确定指标主客观权重，可充分结合工程经验及有功控制效果数据特征的自信息与互信息进行合理赋权，并引入云物元理论将等级边界进行模糊化处理，从而对评价过程存在的不确定性加以考虑，进而结合权重及各方面控制效果计算风电集群有功控制策略的等级隶属度，使评价结果更加客观、准确，为方法筛选与策略安排提供一定的参考价值。针对甘肃酒泉风电集群3 种有功控制策略进行案例分析，验证了所提方法可有效增强评价结果的准确性与合理性，为风电集群有功控制策略的制定提供理论依据。

1 风电集群有功控制策略评价指标体系

风电集群有功控制在保证电网安全稳定运行的基础上尽可能提高各项经济、技术性能，因而综合考量电网运行的安全稳定性、经济性及风能利用水平，构建了如图1 所示的风电集群有功控制策略综合评价指标体系。

图1 风电集群有功控制策略评价指标体系Fig.1 Evaluation index system of wind power cluster active control strategy

1.1 安全稳定性指标

1）频率偏移度。采用频率偏移度评估电网运行的安全性，定义风电集群在统计时期内的最大频率偏移度I1为[5]：

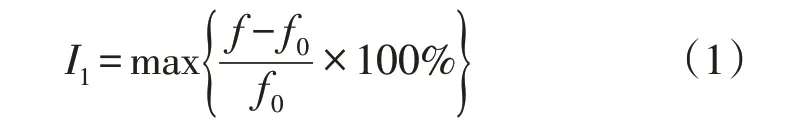
式中：f为实际频率；f0为参考频率。

2）电压偏移度。采用电压偏移度进行评估，定义风电集群并网点在统计时期内的最大电压偏移度I2为：

式中：N为并网点数；Ui为并网点电压；U0为参考电压。

3）集群出力波动指数。风电集群的出力波动对电网稳定运行造成冲击，为评估有功控制策略在降低输出波动的效果，定义集群出力波动指数I3为[5]：

式中：Nt为统计期时段数；Pwt为t时段风电集群有功出力；Pw0为平均出力。

1.2 经济性指标

1）火电厂煤耗率指标。采用火电厂煤耗率指标I4衡量风电集群有功控制对火电厂经济性产生的效果，定义为实际煤耗率ε与最佳煤耗率ε0的最大偏移度。即：

2）线损率。为衡量风电集群有功控制策略对电网整体线损产生的效果，采用线损率指标I5评估经济性。即：

式中：NL为网络线路数；ΔPLi为线路i的有功损耗；Pi为线路i流过的有功。

3）厂用电率。采用厂用电率指标I6评估风电集群有功控制下对整体机组厂用电的影响。即：

式中：Nm为电网整体机组数；Ploss，i为机组i在统计时期内的平均厂用电功率；Pout，i为机组i在统计时期内的平均输出功率。

1.3 利用水平指标

1）弃风率。为衡量风电集群有功控制在风能资源利用水平方面带来的效果，采用弃风率指标I7进行评估，为统计时期内平均弃风功率Pl与集群总装机容量PG的比值，即：

2）发电同时率。发电同时率也称集群效应系数，反映风电集群的综合容量利用率，表征装机利用水平，采用发电同时率指标I8评估有功控制对利用水平的影响，定义为统计时期内风电集群最大出力Pmax与总装机容量PG的比值，即：

2 基于G1-CRITIC法的主客观赋权

对风电集群有功控制各方面效果重视度的合理调节对控制策略的科学制定及综合评价至关重要，为充分利用工程经验及控制效果的数据特征，本文采用G1 法确定各项指标主观权重，同时采用CRITIC 法计算各指标客观权重。

2.1 G1法确定指标主观权重

G1 法又称序关系分析法，是专家根据工程经验确定指标主观权重的有效方法[15]，相较于传统层次分析法在形成判断矩阵时由于思维不完全传递性引入的误差，其预先对指标依照相对重要关系进行单方向依次排序，无需一致性检验，具体步骤为：

1）决策者结合工程经验在指标集中筛选出重要性程度最高的指标，在剩余指标集中再次筛选出重要性程度最高的指标，依此类推，由此可得各指标的唯一序关系。

2）决策者对相邻指标Ii与Ij间的相对重要程度进行评定，得到权重比值，即：

式中：wa，i，wa，j分别为Ii与Ij的主观权重；rij为权重比值，取值为1.0，1.2，1.4，1.6，1.8，分别表示同等重要、稍微重要、明显重要、强烈重要、极端重要[15]。

3）利用式（10）计算指标In的权重wa,n，并利用式（11）递推公式计算其余指标权重，即：

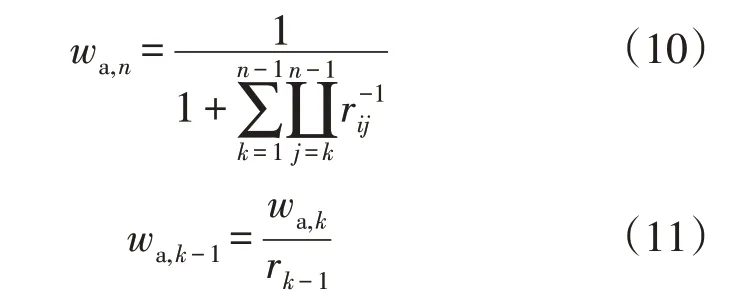
式中：n为指标总数；rk-1为指标Ik与指标Ik-1的权重比值。

2.2 CRITIC法确定指标客观权重

CRITIC 法基于指标数据的标准差与皮尔逊相关系数特征进行赋权，相较于熵权法[15]、变异系数法[16]等传统的客观赋权法，其不仅能够表征指标变量自身的离散程度，且可以衡量指标间的冲突性，从而降低赋权冗余度，使计算结果更加合理，具体步骤为[17]：

1）为便于数据处理，将负向效益指标如频率偏移度、弃风率等进行正向化处理，即：

式中：为正向化后的指标值；xij为负向效益指标值；Xi为各类有功控制策略j下各项指标i的数值；p为协调系数，取0.1。

2）由于各评价指标的物理含义及单位不同，需对其进行无量纲化处理，即：

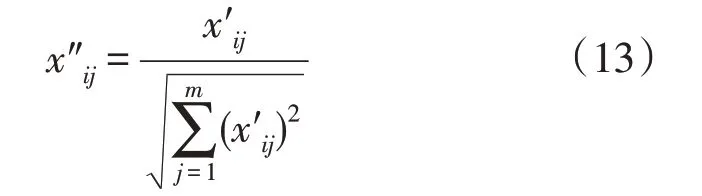
式中：为无量纲化处理后的指标值。

3）为同时表征指标的自信息与互信息，用标准差衡量同一指标在不同控制策略下的离散程度，即：

式中：si为指标数据的标准差；m为控制策略总数。用皮尔逊相关系数量化指标间的冲突性，即：

式中：ρij为指标Ii与Ij的皮尔逊相关系数；为指标Ii与Ij的数据协方差；sj为指标Ij的标准差。

4）利用求得的标准差与相关系数计算信息量，即：

式中：Ci为指标i蕴含的信息量。

5）计算客观权重，即：

式中：wb，i为指标i的客观权重。

主观权重法能够考虑决策者的效益偏好，从而灵活调节指标主观权重，客观权重法充分挖掘指标数据的信息量，且具备较强的数学理论依据，为了同时兼顾两者的优势，避免使综合评价出现主观性过强或未能体现决策者意图的情况，采用平权法确定主客观占比，体现了评价公正性，因此各项指标的组合权重为：

式中：wi为指标i的组合权重。

3 基于云物元理论的等级隶属度计算

由于对指标性能等级的评定存在不确定性，本文引入云物元理论[18]计算风电集群有功控制策略的等级隶属度，其由云模型与物元理论组成。云模型基于期望Ex，熵En与超熵He3 个数字特征，把模糊性与随机性关联到一起，符合人们对概念认知的统一程度与随机性度量，因而可将等级边界模糊化，从而刻画风电集群有功控制策略性能等级评估的不确定性。

物元理论可将指标性能、指标等级及其数值区间统一起来，实现定性分析与定量分析的有机结合[18]。利用云物元理论计算风电集群有功控制策略等级隶属度的步骤为：

1）将给定的等级区间[gmin，gmax]进行标准云转换，即：

2）根据等级划分的模糊性程度给定云模型的超熵He的值，在以En为期望，He为标准差的正态分布中生成随机数E′n，则可以计算各指标的等级隶属度为：

式中：μ为为指标等级隶属度；x为指标数值。

3）结合组合权重向量及各指标的等级隶属度，可得风电集群有功控制策略综合评价等级隶属度向量为：

式中：μr为综合效益对等级r的隶属度；μnr为指标In对等级r的隶属度。

本文所提基于G1-CRITIC-云物元法的风电集群有功控制策略综合评价流程如图2 所示。

图2 风电集群有功控制策略综合评价流程图Fig.2 Comprehensive evaluation flow chart of active power control strategy for wind power cluster

4 算例分析

以甘肃酒泉风电集群[5]为背景做案例分析，大规模风电集群接入甘肃河西电网以750 kV 双回输电线路为主要输电通道，750 kV 敦煌变与酒泉变为风电集群的主要接入点，分别采取3 种集群有功控制策略：（1）策略1：以降低风电集群出力波动为目的的有功控制策略；（2）策略2：以降低网络线损率为目的的有功控制策略；（3）策略3：以增大风电集群发电同时率为目的的有功控制策略。

利用3 类控制策略作用下该地区返回的电网运行数据[1，5，6]计算I1-I7，其中，安全稳定性与利用水平方面的指标通过该地区风电集群的频率、电压及出力情况求解，线损率其样本数据的采集对象为网络所有支路，厂用电率针对全部机组。因此，结合1节中相关定义式计算可得各类控制策略下各项指标的数值，如表1 所示，表征风电集群的有功控制效果。采用G1 法求解各项指标的主观权重；利用表1 样本数据，采用CRITIC 法、熵权法分别计算各项指标的客观权重。权重计算结果如表2 所示。

表1 风电集群有功控制效果Table 1 Active power control effect of wind power cluster

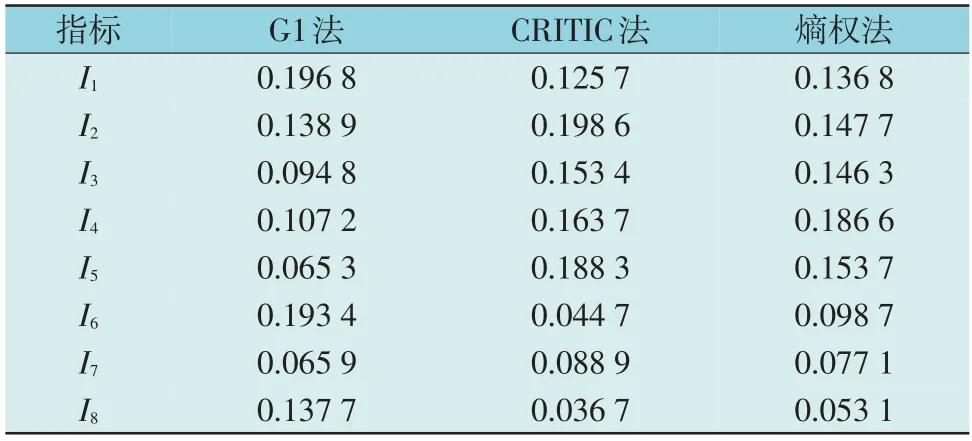
表2 指标权重计算结果Table 2 Index weight calculation results

如果采用熵权法计算客观权重，将无法降低赋权冗余度，进而降低评价的准确性，运行结果显示，CRITIC 法有效降低了频率偏移度、火电厂煤耗率、厂用电率、发电同时率的权重值，且在考虑指标冲突性条件下计算所得的线损率指标客观权重大于火电厂煤耗率指标，而熵权法计算所得的重视度排序则与之相反，因此，CRITIC 法在降低赋权灵敏度过高的同时能够纠正不精确的赋权排序，使评价结果更加客观合理。

结合工程经验[1，6]给出各指标的性能等级划分及其数值区间情况如表3 所示，求解得到各指标的等级界限云模型如表4 所示。

表3 指标等级评价区间Table 3 Index grade evaluation interval

表4 指标等级界限云模型Table 4 Index grade limit cloud model

以控制策略1 为例，表5 为计算所得各指标相对于4 个等级的隶属度。

表5 控制策略1指标等级隶属度Table 5 Index grade membership of control strategy 1

运行结果表明，指标落入所属数值等级区间的概率最大，并沿两侧递减，验证了采用云物元理论刻画评价模糊性与随机性的优势，模糊性表现为等级隶属度的计算结果具有“亦此亦彼”特点，即主观评价等级结果存在落入前后相邻等级内的可能性，随机性则体现在计算结果具备的“正态云”分布特性，与评价过程的主观感受相一致[19]，因此其评价结果应是更为客观的。进而结合G1-CRITIC 赋权结果计算3 种风电集群有功控制策略对优秀、良好、中等、较差4 个等级的隶属度，运行结果如表6 所示。

表6 风电集群有功控制策略综合等级隶属度Table 6 Comprehensive grade membership of active power control strategy for wind power cluster

策略1 以降低风电集群出力波动为目的进行调控，指标信息显示其频率偏移度与电压偏移度的控制效果仍为最优；策略2，3 分别以降低网络线损率、增大集群发电同时率为目的进行调控，指标数据显示，两者在经济性与利用水平方面体现出各自有功控制特性的优势，符合工程实际。根据最大隶属度原则[20-22]，风电集群有功控制策略1，2，3 的综合评价结果分别为中等、良好、优秀，因此综合安全稳定性、经济性与利用水平方面的工程需求，以增大集群发电同时率为目的的控制策略其评价效果最优。当等级边界未作模糊化处理[23-25]时，运行结果为：策略1，2，3 分别隶属于良好、优秀、优秀。因此，结合云物元理论的综合评价在处理评估过程中对概念认知不确定性的基础上，可提高等级评定的准确性，从而使综合评价结果更加合理，为风电集群有功控制策略的制定提供更为客观的理论依据。

5 结论

本文提出一种基于G1-CRITIC-云物元法的风电集群有功控制策略综合评价方法，有以下几点结论：

1）基于评价指标对风电集群有功控制策略进行细化、量化分析，可有效评估控制策略在保证电网安全、稳定、经济运行及提高风资源利用水平方面的性能效果。

2）G1-CRITIC 法合理利用工程经验对有功控制各方面效果进行权重分配，且基于指标的自信息与互信息数据特征，能够提高赋权结果的准确度，使风电集群有功控制策略的综合评价更为合理。

3）引入云物元理论计算综合等级隶属度可有效处理评价过程的不确定性与随机性，为风电集群有功控制策略的制定提供更为客观合理的理论支撑。

值得注意的是，在不同案例中，可根据具体需求对控制策略与评价指标进行更新调整，本文所提的综合评价方法仍适用。本文的控制策略基于单目标优化，未来还需针对多目标优化的风电集群有功控制进行建模仿真，并进一步研究其控制效果对综合评价结果的影响。