活塞式水平弹射装置内弹道性能优化

陈 哲，郭 翔，王志昊，余 瑞，余 剑，邓康清，庞爱民,3

(1 航天化学动力技术重点实验室, 湖北 襄阳 441003;2 湖北航天化学技术研究所, 湖北 襄阳 441003;3 应急救生与安全防护湖北省重点实验室, 湖北 襄阳 441003)

0 引言

燃气弹射技术是利用固体火箭发动机燃烧产生的高温高压的燃气，通过直接或间接的方式快速建压，并推动导弹离开发射筒的发射技术。凭借结构简单可靠、响应速度快、环境适应性好等特点，已被广泛应用于各类导弹的发射过程中。水平弹射主要应用于空基平台发射，有助于避免发动机尾焰的影响，保证导弹姿态的稳定性，提高控制精度。弹射内弹道是评价发射系统整体性能的关键指标，其结构设计的特征参量较多，要想达到理想的内弹道性能及发射效果，需要对各个参量进行合理的设计及优化。

近年来，随着高效搜索算法的不断发展，许多进化算法如遗传算法、粒子群优化算法、差分进化算法、蚁群优化算法等开始被广泛应用于内弹道优化设计中。Sadek等将粒子群优化算法应用于单目标和多目标优化设计，改善了内弹道性能，提高制导导弹的发射安全性。张泽峰等结合改进后的差分进化算法进行了优化计算,使计算结果与测试值相一致。Xu等根据改进的最优排序遗传算法针对内弹道计算中的相关参数的不确定性进行了优化。肖剑等将Pareto遗传算法与无后座炮多目标优化问题相结合，优化结果能有效提高炮口的初速度。Li等将遗传算法应用于内弹道装药设计中，并利用多属性决策方法将优化方案进行排序，有助于得到内弹道最优解。

为了处理弹射内弹道的多目标优化问题，进一步提高弹射整体性能，文中基于零维内弹道理论建立了弹射内弹道数学模型，利用MATLAB软件编制了内弹道仿真计算程序，并能根据相关结构诸元，计算得出导弹运动规律；将仿真计算结果与试验数据进行了对比。利用非支配排序遗传算法的特点：将遗传算法与弹射内弹道数学模型相结合，建立了基于非支配排序遗传算法的多目标优化问题数学模型，进行了弹射内弹道性能优化。

1 弹射装置内弹道模型

活塞式水平弹射装置结构如图1所示。主要包括燃气发生器(高压室)、作动筒(低压室)、活塞杆等部件。其中，燃气发生器是弹射动力源，低压室是形成弹射力的密闭空间。燃气发生器通电点火后，引起内部的火药燃烧，产生的高温高压燃气经过底部的两个喷管流入低压室，低压室处于密闭状态，在高温高压燃气作用下，低压室体积开始增大，燃气发生器作为活塞也开始运动，并通过底部连接的活塞杆间接带动导弹运动，使导弹离开发射筒，完成弹射过程。

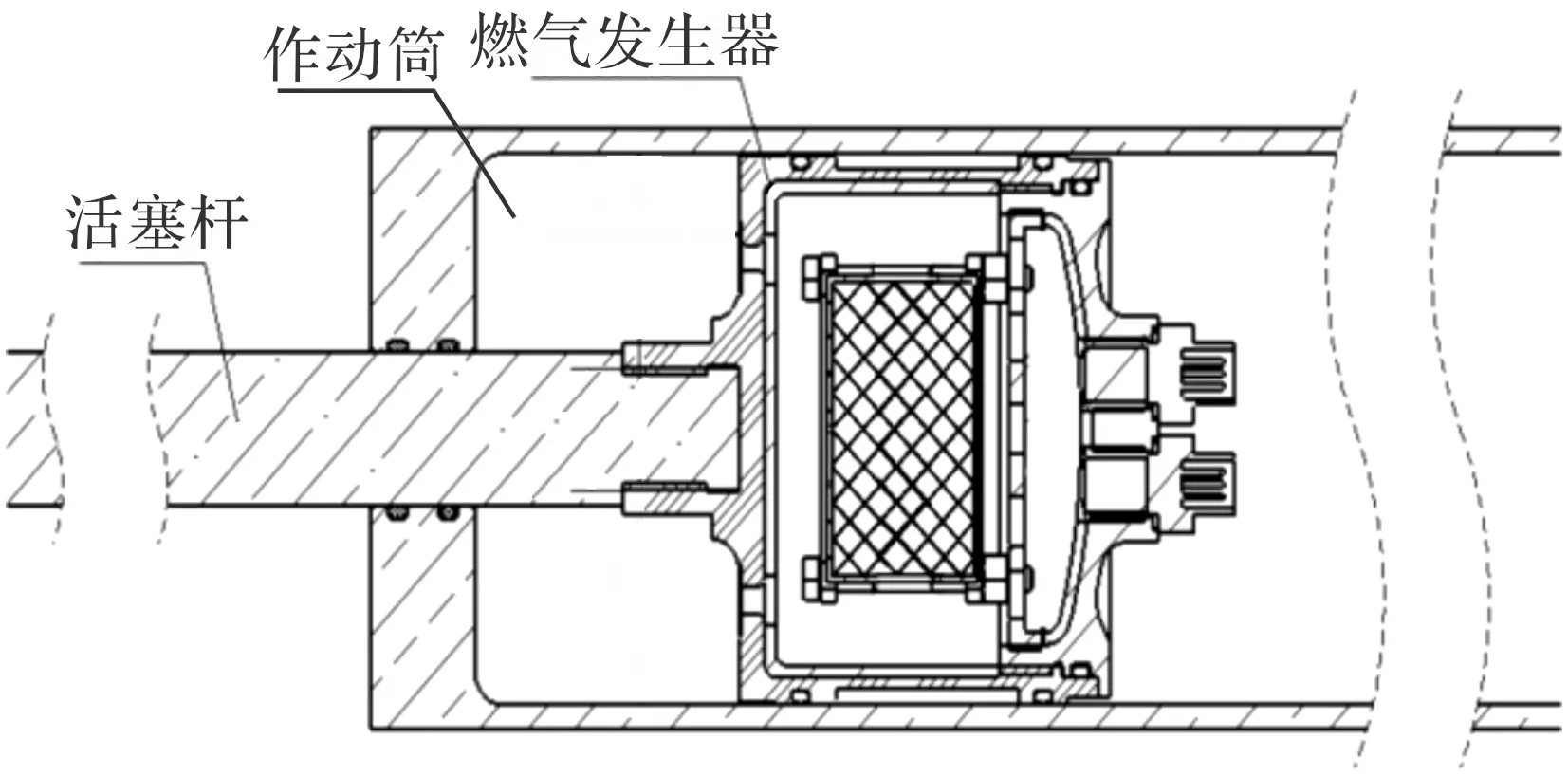
图1 活塞式水平弹射装置结构示意图

活塞式水平弹射装置内弹道方程组的建立基于以下假设：1)不考虑压强在空间上的分布，只考虑其随时间的变化规律；2)高压室喷管内的流动是一维、等熵、准定常的；3)燃气按照完全气体处理，其成分、物理化学性质固定不变；4)火药燃烧是绝热的，高压室燃气温度变化不大。基于水平弹射装置的特点，结合以上假设，建立数学模型如式(1)所示：

(1)

式中：、、分别为高压室燃气压强、自由容积、温度；为火药燃气的气体常数；为装药密度；为装药燃烧面积；为燃速；为喷管的流量修正系数；为喷管喉部面积；为特征速度；为肉厚；为火药的燃速系数；为燃气流量；、分别为总压系数与流量系数；为压力系数；、分别为空气的气体常数、质量；+为开氏温度；为低压室初始容积；为低压室横截面积；为位移；为能量系数；、分别为燃气的定压比热、温度；、分别为空气的定压比热、温度；为导弹质量；为阻力做功；为弹射力；、分别为活塞及活塞杆与内壁的摩擦力；为低压室后段空气阻力。在已知加速度的基础上结合泰勒级数展开式可得到下一时刻的速度与位移。

2 可行性验证

基于上一节所建立的弹射内弹道模型，采用四阶龙格-库塔法，应用MATLAB软件对活塞式水平弹射装置的内弹道进行编程并计算。其中，弹射装置的主要构造诸元如表1所示。

表1 弹射装置的主要构造诸元

同时开展系统联试试验，并实时监测速度和加速度等数据，数值仿真计算结果与试验值的对比如表2所示。

表2 数值仿真计算结果与试验结果对比

由表2可以看出，出筒速度、弹射过载和工作时间的计算值与试验值相差不大，说明所建立的弹射内弹道计算程序是可行的，可以用于弹射内弹道优化设计中。

3 弹射内弹道多目标优化设计模型

文中采用非支配排序遗传算法对弹射内弹道性能进行优化，预期实现短时间、低过载、高平稳弹射。

3.1 遗传算法

遗传算法能在搜索的过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解。

非支配排序遗传算法是基于Pareto最优概念的引入了保留精英策略的改进型遗传算法。为了防止陷入局部最优解，采用拥挤度来维持群体多样性，得到更均匀的Pareto解集，需要对水平相同的解采用拥挤度的概念来进行筛选。

3.1.1 遗传算子

遗传算法有3个基本操作：

1)选择:对种群中的所有个体进行筛选，将每个个体对应的适应度进行比较，适应度高的个体被遗传到下一代中的概率就大，使得群体的适应度值逐渐逼近最佳。选择操作可以避免有效信息的丢失，提高计算速率和全局收敛性。采用锦标赛选择算子进行操作，基本思想是每次随机选取一些个体中，再将其中适应度最高的个体遗传到下一代。

2)交叉:是按照一定的概率从种群中选择两个个体，交换它们的某个或某些位。交叉是产生新个体的主要方法，决定了算法的全局搜索能力。采用算术交叉，即通过两个个体的线性组合而产生出新的个体，交叉概率取0.8。假设以两个个体、进行算术交叉，则产生的新个体为：

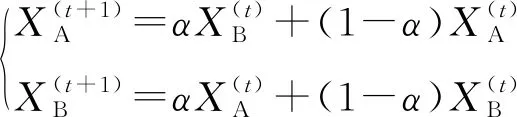
(2)

式中:为参数，可以为常数，也可以为一个由进化代数决定的变量。

3)变异：以较小的概率对个体上某个或某些位值进行改变，生成新个体。变异决定了算法的局部搜索能力。文中采用边界变异，即随机地取基因座的两个对应边界基因值之一去替代原有基因值，变异概率取0.2。

选择、交叉与变异相互配合，共同完成对搜索空间的全局搜索和局部搜索，从而使得遗传算法能够以良好的搜索性能完成最优化问题的寻优过程。

3.1.2 Pareto最优解

弹射内弹道优化问题是多目标优化问题，需要解决含有多目标和多约束的优化问题，多目标优化问题的数学模型如式(3)所示：

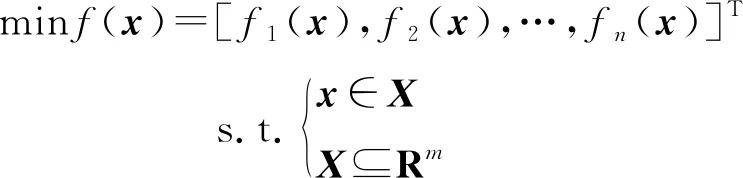
(3)

式中:min表示向量极小化，即目标函数()=[(),(),…,()]中的各个子目标函数都尽可能地达到极小化;⊆为多目标优化模型的约束集。

多目标优化问题中，当某一个目标较好时，其他目标可能会变差，最终优化得到的通常是各个目标权衡后的结果集合，称为Pareto最优解集。

3.2 优化问题数学模型

以某活塞式水平弹射装置为研究对象，选用弹射工作时间、加速度峰值、加速度标准差作为评价指标，其中加速度标准差选用加速度达峰值后的数据来进行计算。由于弹射装置结构及其他因素限制，取优化变量为装药量、高压室初始容积、喷管喉部半径、发射筒初始容积，结合弹射内弹道模型，本优化数学模型可描述为：

min()=[,,]

(4)

根据相关结构，确定优化变量，并设定了一定的范围，为确保弹射效果并优化弹射内弹道，弹射发射时间应小于250 ms，发射过程中导弹所承受的最大过载应小于10，且导弹出筒速度不应低于10 m/s，参考导弹其他发射特征可建立如下约束函数：

(5)

3.3 算法流程

优化流程图如图2所示，可直观看出非支配排序遗传算法的优化过程。

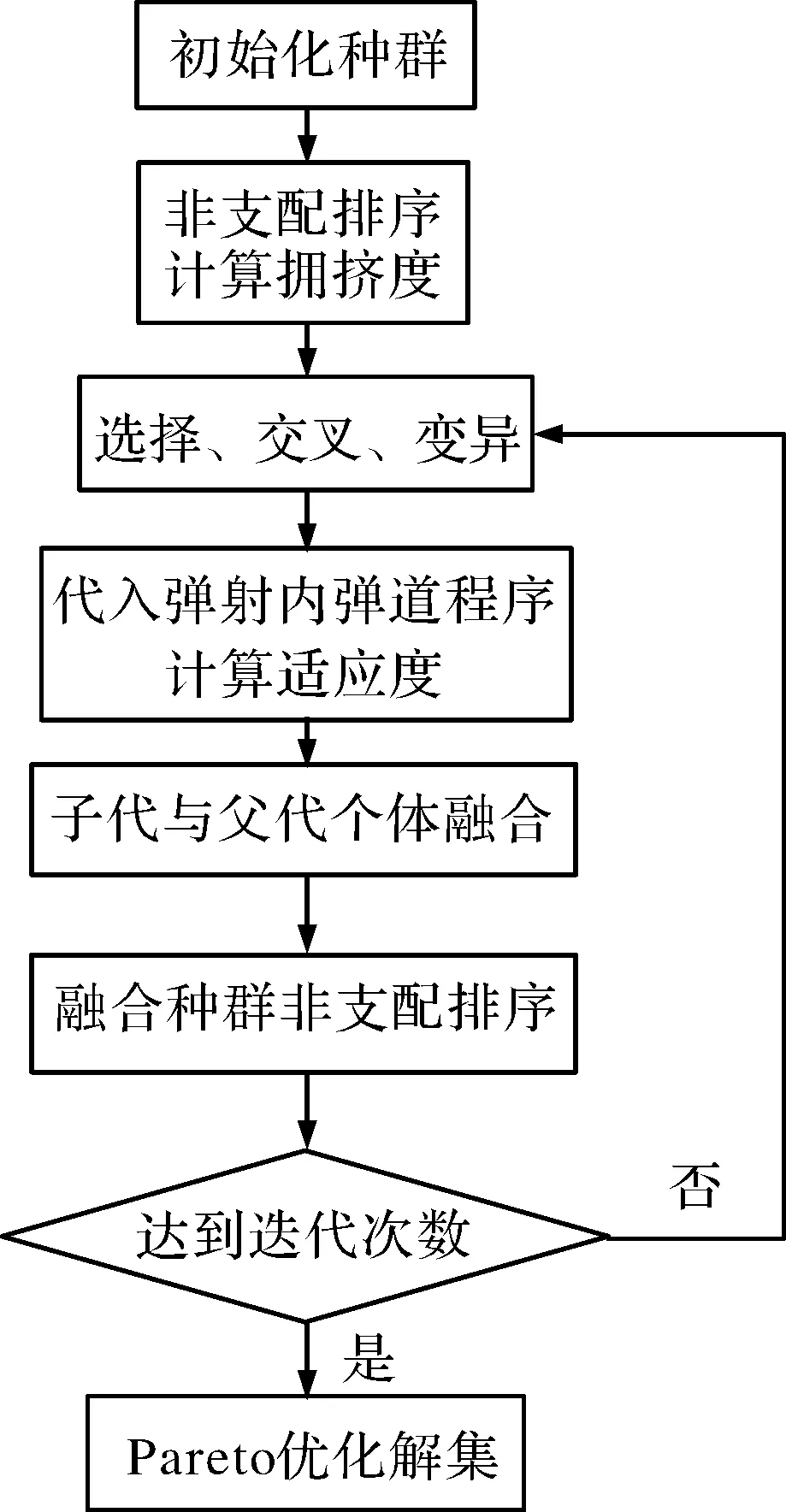
图2 算法流程图

4 算例及结果分析

据上述优化模型的特点，经过反复试验后得出，交叉概率取0.8，变异概率取0.2时，优化算法可以迅速收敛到最优值，初始种群规模为30，终止代数为300，并按照图2给出的流程进行优化计算，得到如图3所示的Pareto前沿。

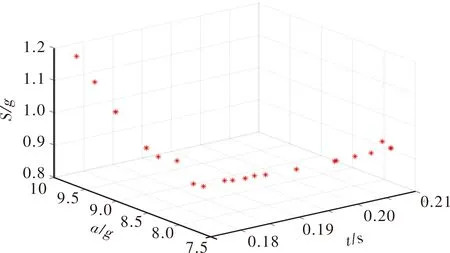
图3 Pareto前沿

由图3可以看出：3个坐标轴分别对应了初期所设定的3个优化目标，即弹射工作时间、加速度峰值及加速度标准差。虽然采用不同的参数会得到不同的优化结果，但所得到的优化解相对集中，为175～210 ms，为7.5～99，为0.81～116，均满足设定的目标范围，证明了这些解都是有效的。同时，得到的优化解集提供了多种选择方案，若偏向于其中某一个目标，则可以选择Pareto前沿中某坐标轴靠近一端的解，即与单目标优化相同；若同时注重几个目标，则可以选择Pareto前沿中间的解，表3所示给出了部分优化解的数据。

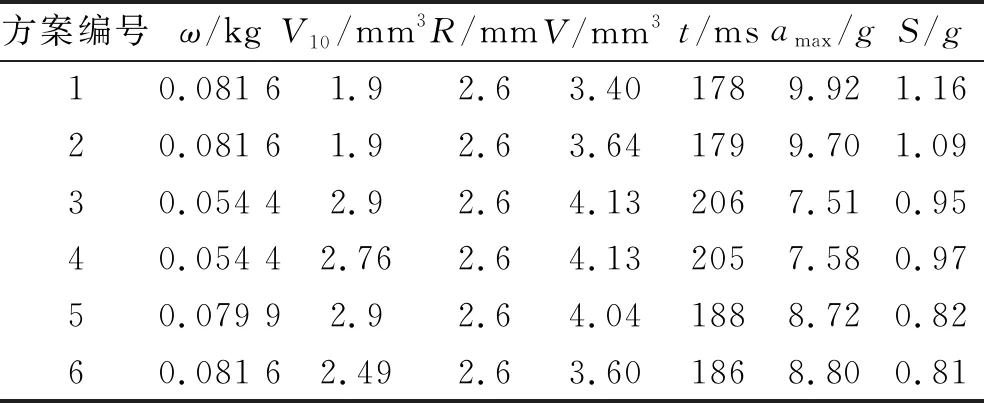
表3 部分优化方案

表3中的数据均可满足基本的优化需求，但根据不同的设计需求，选择不同的优化方案仍是必要的，若偏向于减小弹射工作时间，可以选择方案1和2；若偏向于较小的过载，则可以选择方案3和4；若偏向于提高弹射过程平稳性，则可以选择方案5和6。

5 试验验证

为了验证优化效果，选择加速度平稳性最高的点编号6作为设计方案，将设计方案代入到弹射内弹道计算程序中进行了计算，并对修改后的弹射装置开展了常温下(20 ℃)水平弹射试验，将计算结果与试验数据进行了对比，并将优化后的方案与原方案的过载图进行了比较，结果如图4所示。

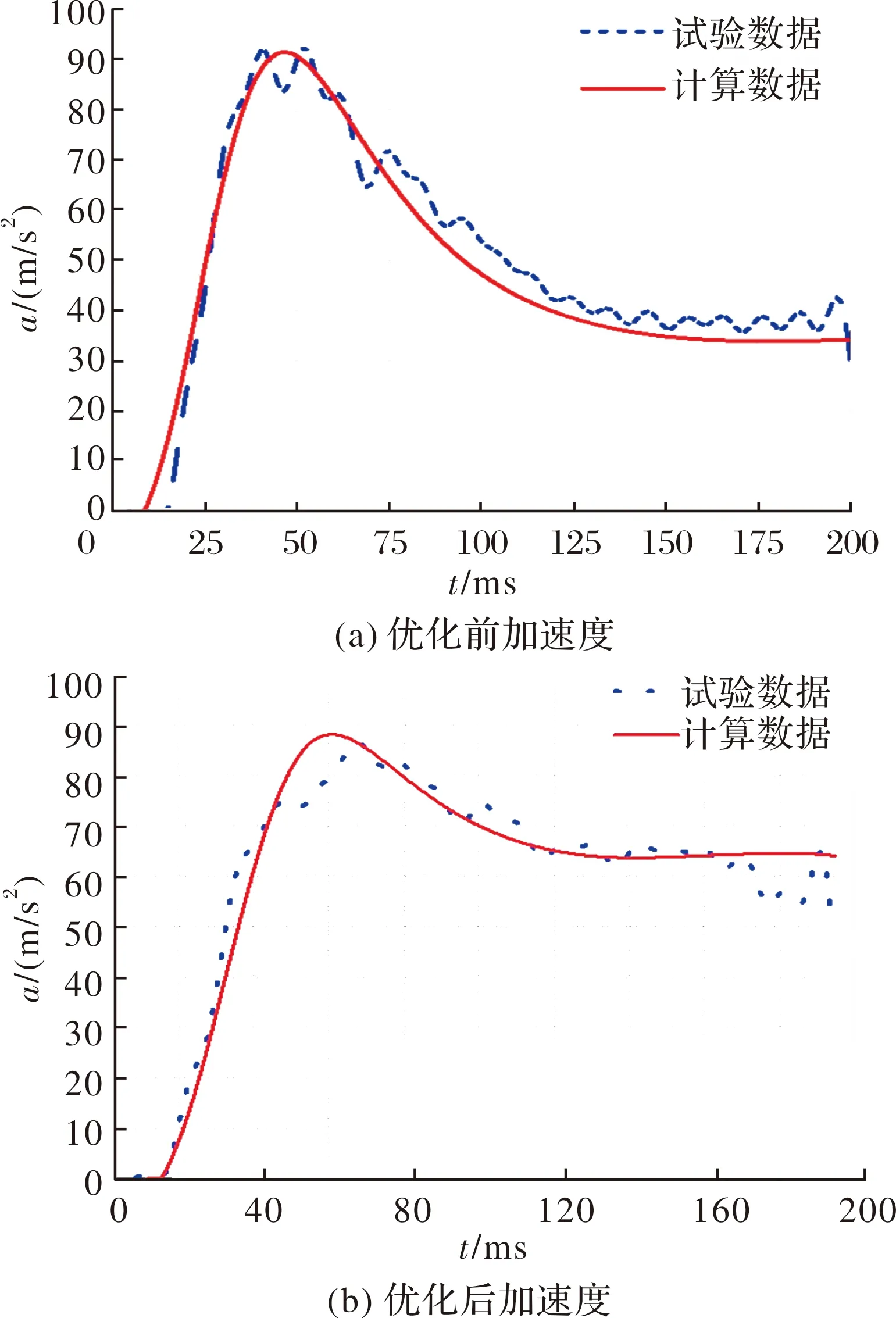
图4 加速度曲线对比图

从图4可以看出，改变装药量、初始容积、喷管等数据后，弹射过程中的加速度峰值有所降低，加速度曲线平稳性显著增加，弹射后期，原方案加速度迅速降低，优化后，加速度能保持在一定水平。优化前后弹射过程时间、速度和加速度的数据对比如表4所示。

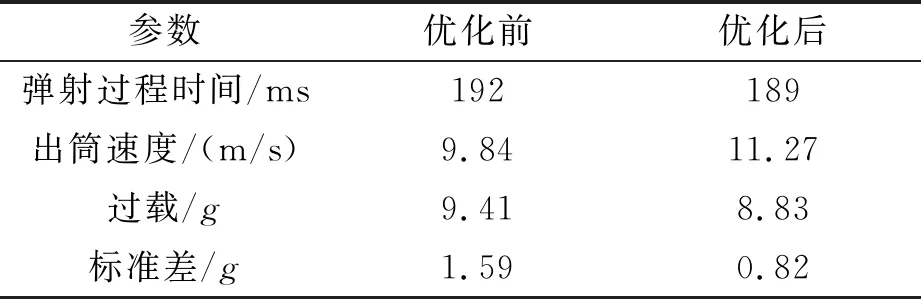
表4 优化前后参量比较

从表4的数据对比可以看出，弹射工作时间相比原方案减小了3 ms，速度相对于原方案提高了1.43 m/s，过载减小了058，标准差减小了077，这证明了将非支配排序遗传算法应用到弹射内弹道的优化是可行的。

6 结论

将非支配排序遗传算法与弹射内弹道相结合，对内弹道性能进行了优化。选取优化解集中的一个作为设计方案进行了计算并开展了试验，优化后的主要目标函数，弹射过程时间减小了1.6%，出筒速度增加了14.5%，过载降低了6.1%，加速度标准差减小了48.4%，各项数据均在裕度范围内，可以满足设计要求。

此外，根据实际情况需要，可以在所得到的优化解集中选择不同的设计方案，各个优化变量也都在预期范围之内，可为弹射装置的后续改进设计提供指导。