一种利用数据集成的基础地理信息数据改化方法

张 萌 杜为财 郭 霄

1长安大学地球科学与资源学院，陕西西安，710061

2 61175部队，江苏 南京，210000

3长安大学地质工程与测绘学院，陕西西安，710061

基础地理信息数据作为统一的空间定位框架和空间分析的基础［1］，在国民经济生活中发挥着重要作用，将要素表达详细、覆盖范围广的基础数据改化为军用标准（简称军标）数据是军民融合的重要内容，两者的多尺度联动更新也是发展的必然趋势［2］。由于基础数据与军标数据的使用目的等存在差异，在数据改化时，有些军标数据的重点需求要素在基础数据中不被重视，出现现势性差甚至缺失的情况。

多源空间数据集成主要指对已有的空间数据进行合并、提取、布尔运算、过滤等操作，以得到新的数据［3］。目前对数据集成的研究多集中于其实现模式和技术手段上，侧重GIS的集成，如GIS数据集成模式的探讨［4⁃6］、数据集成框架和实现方法的研究［7⁃9］，而对空间数据本身的集成方法和过程的研究较少。

针对上述问题，本文提出一种将其他来源的数据与基础数据进行集成的方法，以达到要素更新和质量改进的目的，同时提高已有数据的利用效率；并在MapStore平台下进行实验，以检验该方法的可操作性和实际意义。

1 数据集成与改化

1.1 数据集成方法

由于多源数据生产和更新时各自的目的不同，彼此之间存在模型、存储格式、语义表达、比例尺等诸多方面的不一致。数据集成是将多源数据在逻辑上或物理上进行有机集中，从而实现地理信息共享［4］。在集成的基础上还可以进一步进行数据融合，将这些存在差异的数据加以综合和互补，消除冗余和矛盾。多源地理空间数据的集成和融合可以避免重复劳动，最大程度地发挥已有数据的能效，提高数据质量。此外，还能产生比单一数据源更精确和完整的估计或判断［10］，对空间分析和决策支持具有一定意义。

本文在集成中对数据进行了处理，使数据库内容发生改变，这也属于数据改化的范畴。集成后的数据仍以基础数据形式存在，并被改化为军标数据，故在集成中要消除其他来源数据与基础数据的差异，集成的过程分为预处理和要素集成两部分，对数据的操作主要是合并和提取。

1.1.1 集成预处理

把集成需要进行的预处理定义为两类：①将其他来源的数据与基础数据在数据模型、空间基准、语义编码方面进行统一［11］，本文主要指空间基准的统一。②数据自身的要素关系处理。首先，空间基准的一致是数据集成的基本前提，也是多源数据共享的基本保障。空间基准的统一包括坐标系统统一、地图投影统一和高程基准统一［11］。其次，矢量数据自身的要素关系具有一定的复杂性，容易出现重叠、裂隙、伪结点等问题，集成前要进行处理，确保自身的点、线、面数据关系正确。

1.1.2 要素集成

地理空间数据是地理实体的空间特征及属性特征的数字描述，故空间对象在不同数据中表达的差异主要分为几何位置（图形上）和属性数据（语义上）两类；对于现势性不同的数据而言，这种差异往往具有更新的价值。数据集成的内容主要在于图形和语义两方面。

1）图形集成。对于同一区域不同来源的空间矢量数据，相同要素往往重复表示，但存在几何位置、几何形状、空间关系等的差异，图形集成指的是集成后数据中实体要素几何位置的确定。本文直接选取其中一种数据的几何位置作为改化后数据的几何位置。应视具体目的和数据特点，结合唯一性原则、几何精度原则、现势性原则等综合选取出所需数据的几何位置作为集成数据的要素几何位置［11］。本文基础数据与其他来源数据的图形集成是按要素选取进行的，集成之后，导入的要素可能会与基础数据的要素发生要素关系错误，需要进行编辑和处理，遵循的原则是只对其他来源数据要素的几何位置、形状等进行编辑和修改，保持基础数据的几何位置不变，从而最大程度地保障集成数据的精度。

拓扑地图模型对集成数据处理的核心技术是对地理实体的几何对象进行拓扑化处理，以实现几何对象的共用，并保障拓扑关系的唯一性，引用图的概念来描述几何对象间的层次关系，用度来刻画单个结点的属性。具体方式是建立几何对象间的几何关系图来完成集成数据要素关系错误的处理，大致过程如下［12］：首先，将几何对象重新划分为4类元素（点、线、复合线、复合面），抽象成图中的顶点，建立起图的顶点集；然后，将4类元素间的位置关系和构成关系抽象成图中的边，建立起图的边集，再建立几何对象的几何关系图。本文以面实体对象为例进行说明。如图1（a）所示，线L1、L2、L3、L4通过结点P1、P2、P3、P4构成复合线CL1，它们共同构成复合面CA1，那么按照图和度的理论，CA1的顶点集为｛P1，P2，P3，P4，L1，L2，L3，L4，C1，A1｝，它的几何关系图如图1（b）所示。对任意两个实体，均可按上述流程进行拓扑化处理，再构建几何关系图进行交和并的运算，依据几何位置辅助判断实体的拓扑关系，再进行错误要素关系的处理，如消除裂隙、扣除重叠的面等。

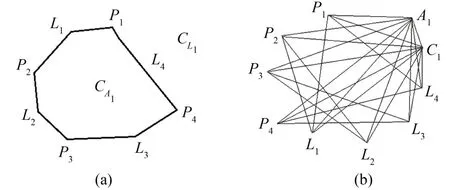
图1 面实体的几何对象及几何关系示意图Fig.1 Diagram of Geometric Object and Geometric Relation of Polygon Entity

2）语义集成。对于同一地物的属性描述，在不同数据中，其字段名称、字段数量、编码规则、编码长度均可能有差异；而对于不同的地物，不同数据也易产生一对多（同类地物描述术语不同）、多对一（同一描述术语所指地物不同）等冲突和矛盾。语义集成指的是消除这些矛盾，将参与集成的数据的属性结构进行统一的过程，通过要素属性结构转换来实现。在保障数据精度的前提下，根据用户对集成后数据的不同需要，用不同方式进行处理。本文保留基础数据的属性结构，将其他来源数据的属性结构进行了转化。此外，也可以从原始数据中抽取集成所需的属性组成新的属性结构［4］，同时按照语义转换方法对属性值进行转换。

需要指出的是，本文指出的多源地理空间矢量数据在图形和语义上的集成更接近数据融合的概念，关于集成的过程中是否存在数据冗余的问题，由于本文方法使集成后数据的几何位置数据或某种属性数据成为了基础地理信息数据中对应的数据，故不存在数据融合中的实体匹配问题，没有达到数据真正融合的层次。集成后的数据应是按照用户目的结合了原始数据各自优势或特点的、几何位置协调、属性结构一致的数据，在功能和地位上与集成前的数据相同，在本文中作为中间数据继续参与后续军标改化，其他情况下也可直接成为成果数据。

1.2 数据改化内容

对数据库内容进行符合目的的改化，主要考虑改化前后数据的要素分层、属性选取、编码原则等方面的差异，基础数据改化为军标数据主要包括以下内容：

1）要素对应及改化。将存在语义差异的基础数据和军标数据的要素进行对应，主要有3类：①对于命名原则差异导致的同一要素在基础数据和军标数据中名称不同的情况，对要素进行辨别后再对应。即便是名称一致的，也可能存在由采集标准差异造成的实际内容不同的问题，例如，道路要素以边线或中心线表示是不同的。②对于要素分类分级差异导致的同一要素在基础数据和军标数据中表示不同的情况，对要素进行再分类，如火车隧道、汽车隧道与隧道的不同。③由于基础数据和军标数据的表达内容有差异，某些军标数据需要的要素基础数据不具备（如军事要素），或基础数据中的某些要素军标数据不需要，这种情况下应对相应数据进行补充或删除。

2）属性改化。与语义集成的原理相似，属性改化是依据基础数据和军标数据要素属性需求的不同，从基础数据要素的属性项中抽取出军标数据所需的属性，组成军标要素属性表。

3）拓扑关系重建。完成基础数据的要素和属性改化后，基础数据的要素拓扑关系不一定是军标数据的拓扑关系，故还要进行拓扑关系的整改。

1.3 技术路线

将数据集成方法嵌入数据改化流程，技术路线如图2所示。先进行预处理，再进行图形和语义的集成，形成集成数据并进行处理。军标改化流程如下：①分析改化数据的要素类别和属性差异，军标数据不需要的要素可不建立对应关系，需要转换的要素则根据要素编码进行一一对应，对于多对一问题，以基础数据的属性项的值来区分，对于一对多关系，则利用SQL语句来进行限定和区分，赋予要素正确的属性，完成要素改化。②依据用户需要，为改化后军标数据挑选需要的属性字段建立起属性结构，用转换集来完成国标属性结构的转换，以完成属性改化；如果基础数据的拓扑关系不满足军标要求，还需要进行拓扑关系的整改。③将与其他数据集成后的基础数据改化为符合标准的军标数据。

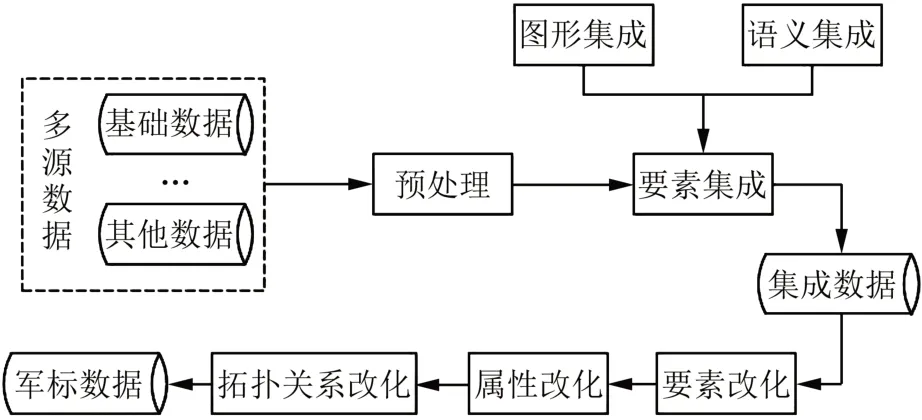
图2 技术路线Fig.2 Technical Route

2 改化实验及精度分析

2.1 改化实验

本文选取陕西省榆林市某县的1∶1万基础地理信息数据作为基础数据，同幅地理国情监测数据中的地表覆盖分类数据（简称国情数据）作为其他来源数据进行实验，将去除植被层的基础数据和国情数据的植被层数据在Map Store下进行预处理和集成，并对集成后的数据进行关系处理，从而进行军标改化。实验可看作是按照现势性原则选取国情数据的植被要素对基础数据进行的更新，故实验中赋予基础数据较高的优先级，并在精度验证中以基础数据的规定为标准。事实上，由于国情数据具有更新周期短、精度高、覆盖范围广等特点，将其应用于基础数据更新可以节约成本、提高效率［13］。

MapStore是基于拓扑地图模型开发的制图与建库数据一体化的生产与管理软件平台，能够利用多源数据编图并输出各种格式的成果。在实际生产应用中，MapStore软件能根据具体情况定制要素模块，减少地形图的编辑工作量，数据改化效率较高［4］，其模型和生产一体化的优势解决了制图与建库数据的联动问题，为生产带来了极大的便利。

集成的预处理主要包括数据坐标系的统一和各自要素关系的自处理。属性集成是利用平台的转换集功能实现的［14］。图形集成方面，依照用户目的和现势性原则选取，植被要素几何位置由国情数据确定，其他要素的几何位置由基础数据确定。对于产生的矛盾和冲突（尤其是面层数据），在构建拓扑后利用Map Store对其进行自动或半自动处理。实验中需要进行的处理有图3（a）所示的面要素重叠部分的扣除、图3（b）所示的微小植被面的消除、图3（c）所示的面裂隙的填补等。其中，可通过设置阈值的方式来查找小面，再将其与邻近大面合并或直接删除；可通过捕捉对应特征结点后移动点投影的方法消除裂隙。这些空间关系的运算和处理，都是Map Store通过分析对象的几何关系图运算结果得到拓扑关系后进行的［12］。

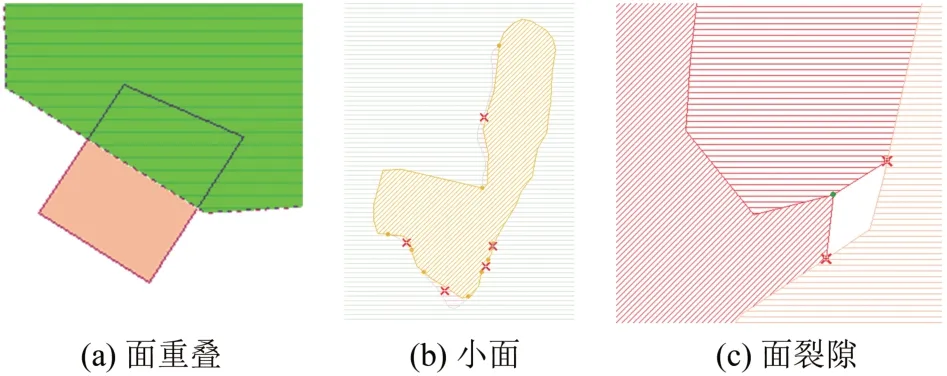
图3 要素关系不正确的情况Fig.3 Cases of Incorrect Relationships of Elements

实验对象仅是植被要素，故本文以原基础数据中的植被数据为标准，将所得的集成数据中的植被数据与其进行对比，效果如图4所示。

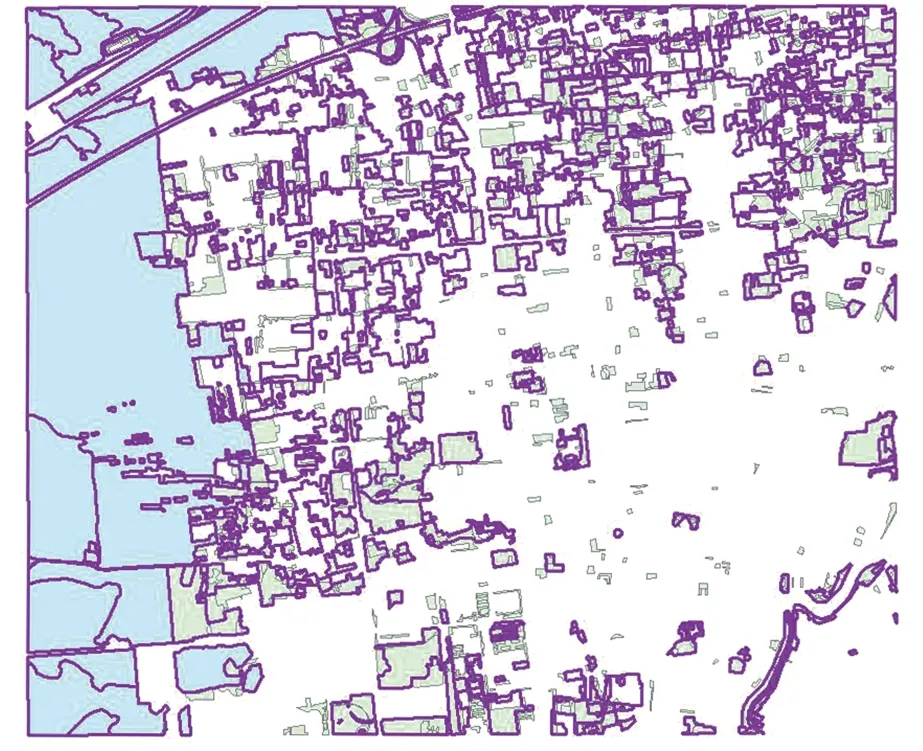
图4 基础植被数据与集成后的数据Fig.4 Basic Vegetation Data and Integration Data

实验中集成数据的植被与原基础数据的植被在几何位置上存在误差。主要有以下几点原因：

1）国情数据与基础数据的数据采集标准和方式不一致，产生了与数据处理过程无关的固有误差。

2）国情数据与基础数据现势性的不一致也导致了固有误差。需要说明的是，实验目的是检验集成后的数据精度是否满足要求，故本文选用的是现势性一致的数据，后续生产中应选用现势性更高的国情数据，以达到更新的目的。

3）图形集成后，为使数据关系正确，本文对植被数据进行了编辑，与经过完整制图综合的基础数据存在差异。

2.2 精度分析

MapStore平台的转换集功能已被证明可以较好地实现属性转换［14］，故仅对实验图形集成结果的精度进行分析。在矢量地形数据规定中，规定测绘成果与实地位置点的中误差为精度指标，在基础数据的位置精度分析中也常进行实地检测［15］。本文则以集成数据与基础数据的标准差为精度标准。

对实验误差进行统计和分析后，将误差评定分为两类，第一类以点为单位，称为点误差，产生此类误差的基础面与集成数据的面对象重合度高，且形状简单而规整，易于寻找特征结点，如图5所示，以对应特征结点坐标差（Δx，Δy）和特征结点的欧氏距离d衡量，经过反复验证，一类误差中d小于15 m比较合适。

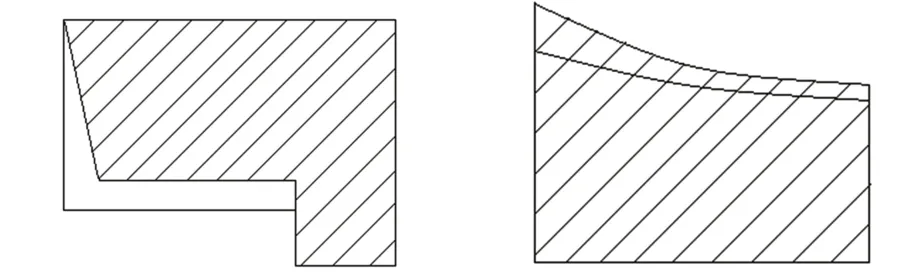
图5 第一类误差Fig.5 TypeⅠError

如图6所示，当d>15 m，或基础面与集成面图形差别大难以寻找对应特征点时，或集成数据缺失无对应特征点时，误差为第二类误差，称为面误差，以基础植被面与集成植被面面积差（Δs）衡量。

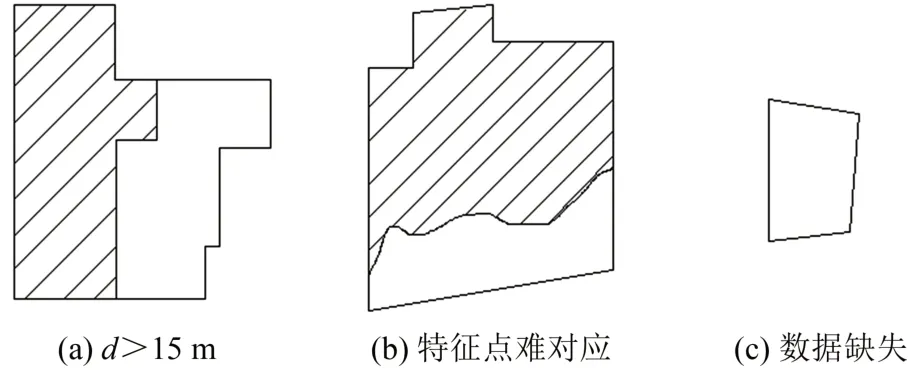
图6 第二类误差Fig.6 TypeⅡError

对第一类误差进行分析，采用抽样法将图幅分为等面积的8个区域，在每个区域随机选取误差不为0的20对特征结点，共160组数据，记录其坐标差和欧氏距离，结果如表1所示。Δx和Δy的正态分布曲线分别如图7（a）和图7（b）所示。

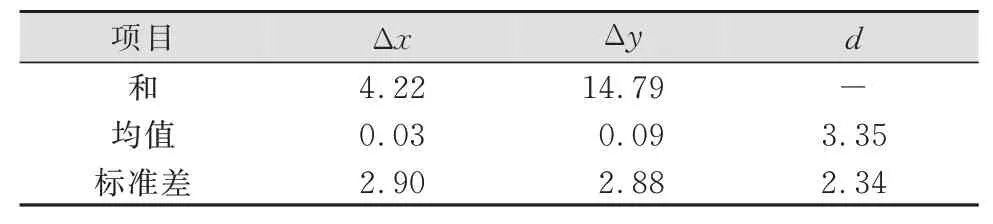
表1 第一类误差值/mTab.1 Values of TypeⅠError/m

按照1∶1万基础数据的精度指标规定，地物点平面位置中误差在平地地区为5.0 m。而实验中Δx、Δy、d的标准差分别为实地距离2.90 m、2.88 m和2.34 m，可以视为满足精度要求。

对第二类误差进行分析，从全图和随机选取的近1/5图幅面积的样本区两个维度进行评价，结果见表2。样本区误差Δs的正态分布曲线见图7（c）。

表2 第二类误差值Tab.2 Values of TypeⅡError

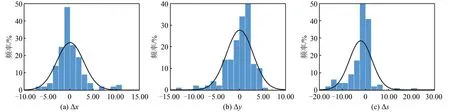
图7 Δx、Δy、Δs的正态分布曲线Fig.7 Normal Distribution Curves ofΔx，Δy andΔs

以1∶1万基础数据的精度指标规定的地物点平面位置中误差5.0 m作为面误差阈值，可以得到，集成数据的误差满足要求。在样本区集成数据和基础数据的误差的均值仅为−2.08%，全图幅误差值也仅为−3.36%，对于实地面积而言，误差可以接受。

综上，矢量数据的集成可以在精度上达到集成前数据的要求。而且，采用更高现势性的国情数据可以在某种意义上实现基础数据的更新，避免了外业测绘，节省了工作量。在实际生产中，利用此方法可以进行不限于植被要素的缺失数据的补足或者现势性不强数据的更新。该方法在技术上可行，精度上达标，具有一定实际意义。

3 结束语

在基础地理信息数据改化为军方数据的过程中，可以通过数据集成来提高要素的现势性和质量。本文探讨了这一方法的可行性与意义，并通过实验证明了其可行性。该方法已被成功运用于福建省数据改化，效果优良，可以提高数据质量和生产效率，具有一定应用价值。然而在已进行的改化中，参与集成的数据的预处理的复杂性和集成的层次相对较低，若数据源的条件改变，可能会出现新的问题，仍需要进一步研究。