基于直接测量和簿记复合法的动力电池SOC估算

0 引言

SOC 表示存在的电荷或能量，在一般情况下， SOC具有以下几种含义：电池的实际 SOC，即估算的数量；估算的 SOC，即计算变量；显示出的 SOC。本文将使用以下定义:电池内部的电荷(以 [Ah]为单位)。SOC 反映了一个估计值。SOC 也可以用最大可能充电量的百分比来表示，例如在条形图上，0% 表示电池没电，100% 表示电池已满。

分析可知，实际触发角由锁相环输出的同步初相位及实际换相线电压共同决定，与直流侧电流无关，因此分别对不计谐波和计及三次谐波时计算实际触发角，与PSCAD运行结果进行比对，以YD侧为例，逆变器两侧的输入量如表4所示，实际触发角和换相角运行结果如表5和表6所示。

电池管理系统的任务之一是跟踪并确定电池的荷电状态 (SOC)。SOC的信息可用于控制充电和放电，并可向用户发送信号。当SOC值用在控制充电时，SOC指示不准确的影响会更加严重，如电池未充满电，电池充电的次数将比实际需要的更频繁，这将导致电池更早的磨损，如电池过度充电，会导致循环寿命降低。本文将对现有的SOC估算方法进行分类，并给出一些实际应用案例，再次基础上，针对某款锂离子电池开发使用新的SOC估算方法，进行实验验证获取测量结果，并将这些结果和之前SOC估算算法进行比较，从而得出结论。

1 SOC测量方式

1.1 直接测量法

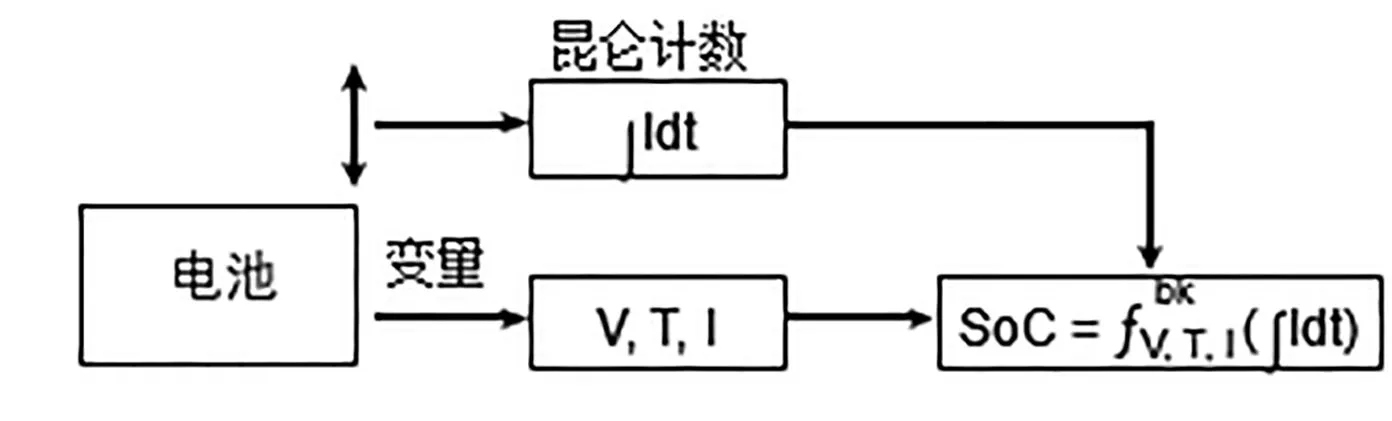
直接测量方法利用测量的电池变量与SOC的关系。电池变量有电池电压 (V)、电池阻抗 (Z) 和电压弛豫时间 (τ)。此外，这些电池变量绝大多数和温度(T)有关；因此，除了测量电压或阻抗外，还须测量电池温度。被测电池变量与SOC之间的关系函数f

，存储在系统中。基于直接测量的SOC系统的基本原理如图1所示。

针对不同的建筑——住宅、非住宅、人员密集场所、老年人照料设施、幕墙建筑，同时按照不同的保温型式——内保温、外保温、夹芯墙保温、屋面保温，并结合建筑的高度，《建规》分别规定了保温材料的燃烧性能等级以及构造要求。其中，关于外墙保温，《建规》的主旨是大力推广应用A级不燃性的保温材料，严格限制使用可燃性的保温材料以及严禁使用易燃性的保温材料。

“现在我在我的家庭里，在那些最好的，最亲爱的人们中间，比一个陌生人还要陌生。”[6]411卡夫卡不止一次地这样意味深长地抱怨:“不幸的童年几乎毁了我的一生”。[4]461-501

1.2 簿记系统

簿记系统是基于测量和集成原理。这可以表示为库仑计数，即“计算流入或流出电池的电荷”。当所有施加到电池的电荷可以在任何条件下、任何时候检索时，这将产生一个准确的系统。基于簿记的SOC系统的基本原理如图2所示。

竹韵长长地松了口气，瘫软在椅子上站不起来。海力拍了拍她的肩头说，坐着别动，好好歇一会，我去交费。说完就快步离去，竹韵看着海力匆匆离去的背影，心中再次涌出一阵感动……

其中

=1,2 或 3。确定

的精度 Δ

将在下面进一步讨论。

与直接测量系统的一个重要区别是函数f

中存在变量“时间”。时间t 是从晶体振荡器 (Xtal) 获得的。因此，存储器必须始终与电池组保持连接。当电池组连接到设备时，设备内部的微控制器可用于计算SOC并将定期SOC更新存储在电池组的内部存储器中。误差会随着时间的推移在簿记系统中累积，可能的误差源包括测量误差和函数中补偿的有限精度。因此，必须校准系统，估计的SOC被重置为校准点中的假定值。在大多数实际系统中，函数中的补偿是经验性的。然而，当电池处于尚未推导出经验方程的情况下，便无法准确进行估算，另外在实际系统中，当参考条件过于全面，系统可能太复杂。

1.3 自适应系统

实际情况中状态之间的转换可以这样理解。算法在t=0时处于平衡状态，因为此时有小于或等于I

的电流流出电池，电池电压稳定。后一种情况可以通过计算电池电压随时间的导数并将其与参数dV/dt

的值进行比较来检查。SOC是在 EMF 方法的帮助下确定的。大于I

的电流在 t=1000s时从电池中获取，然后电池电压下降。算法从平衡状态转变为放电状态。除了SOC之外，系统还会根据该状态下的SOC值来估计trem。放电电流在 t=1600s时变为小于或等于I

的值，进入过渡状态。SOC由放电状态和过渡状态下的库仑计数确定。库仑计数在过渡状态继续进行，因为在该状态下仍有小于或等于I

的电流流动。电池电压放松了 t=2400 s，然后算法再次变为平衡状态。

3.1.2 实验2条件设置

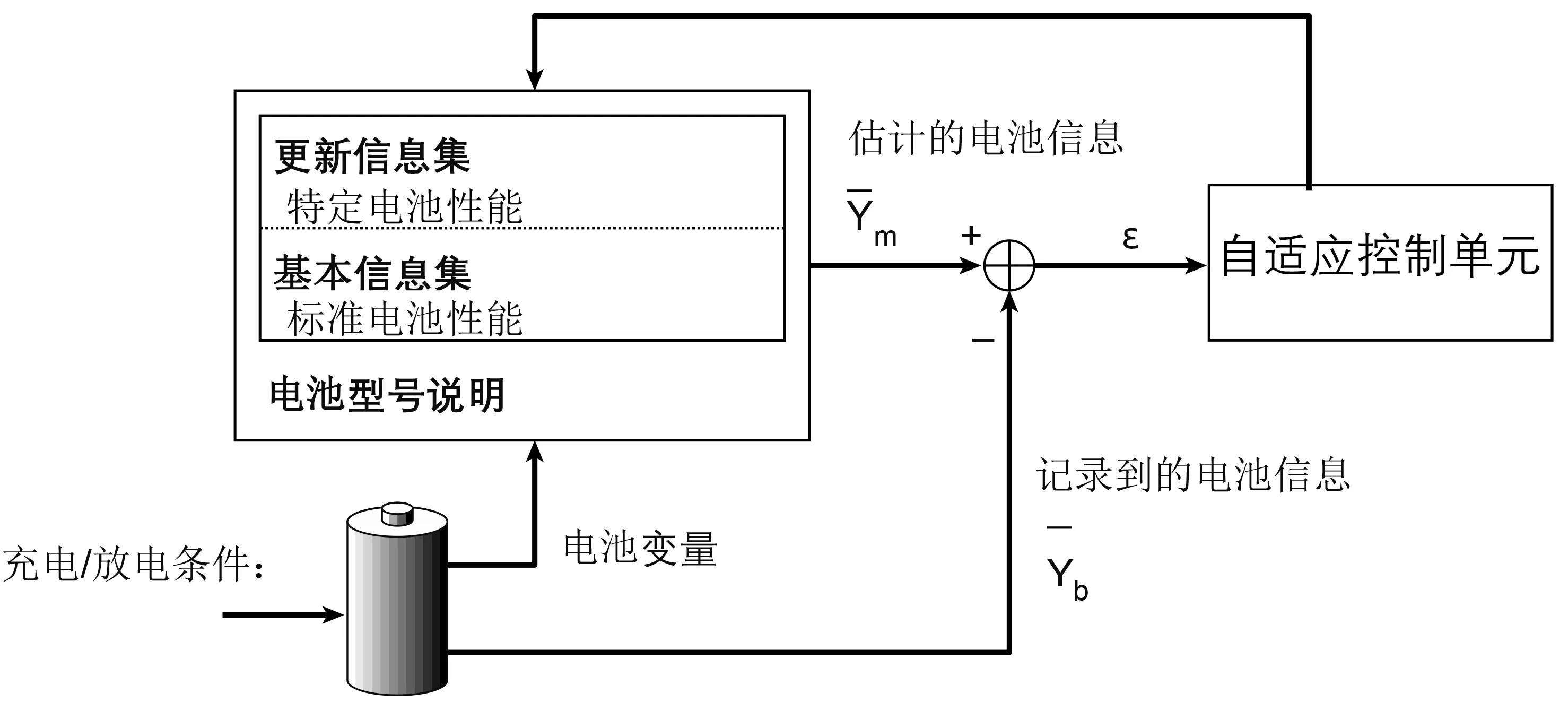
模型的适应性基于Y

与电池的比较向量 Y

。它产生一个误差信号ε，该信号被输入到自适应控制单元。该单元通过更新参数值甚至更改模型描述来更新模型中的信息。因此，该模型根据系统所连接电池的特定行为进行调整，并将估计值和观察值之间的误差降至最低。

SOC系统需要某种适应性来考虑电池行为随时间的变化。在文献中可以找到许多成功应用适应性的例子。然而，假设通过简单地添加学习能力算法，电池模型最终会计算所有相关的电池行为以实现准确的SOC估计，这在很大程度上取决于电池本身，包括电池的使用条件。系统SOC的准确性受到系统误差和随机误差的限制。系统错误是由于系统中不正确或不完整地包含电池行为而导致的。例如，当在簿记系统中未考虑剩余容量的放电电流依赖性时，估计中将出现系统误差。因此，大多数SOC系统通过定义安全裕度或储备容量来实现，以考虑估计中的所有不确定性。当指示显示剩余容量的 0% 时，备用容量仍可使用。但这导致更大的系统误差值，一般来说，系统中描述的电池行为越不准确，系统误差就越大。随机误差是由相同类型电池的行为扩散和测量不准确引起的。在SOC系统中，随机误差被作为系统精度定义的基础，主要以测量精度的形式出现。这可以通过在系统误差很小甚至可以忽略的条件下定义系统误差来实现。然而，系统误差变得明显大于随机误差，尤其是在非标准条件下。这会导致精度低得多。

2 SOC测量新算法

本文新提出的SOC系统是直接测量系统和簿记系统的组合，所提出的算法在五种不同的状态下运行:(1)初始状态；(2)平衡状态；(3)充电状态；(4)放电状态；(5)过渡状态。系统的估计可以在任何状态下以百分比表示的SOC值和有效放电条件下可用的剩余使用时间的形式显示。

当电池首次接入到SOC系统时，算法在初始状态启动。然后，算法会根据电池是充电、放电还是处于平衡状态切换到适当的状态。仅当电池已与系统断开连接并重新接入到系统时，才会重新进入初始状态。初始状态下的SOC是通过测量电池电压并借助 EMF 曲线将其转换为SOC值来确定的。

小于或等于I

的电流从电池中流出或流入，并且电池电压已从先前处于平衡状态的电流中平衡。参数I

在系统中定义。

当电池以大于I

的正电流充电时，算法处于充电状态。当电池以绝对值大于I

的负电流放电时，即处于放电状态。SOC由两种状态下的库仑计数确定。除了SOC，还在放电状态下估计trem。当进入充电或放电状态时，用于库仑计数的SOC的起始值总是已知的。当状态从初始或平衡状态进入时，借助 EMF 方法获得该起始值。或者，可以从放电状态进入充电状态，反之亦然。在这种情况下，也可以使用起始值。

在从充电或放电状态到平衡状态的变化期间进入过渡状态。该状态下电流小于等于I

。与初始状态一样，需要确定是否可以进入平衡状态的条件，电压必须稳定或松弛以允许过渡到平衡状态。如果情况并非如此，并且大于I

的绝对电流再次开始流动，则系统会转换回充电或放电状态。只要电池电压没有完全放松，库仑计数就会在过渡状态下继续。

设计准确的SOC系统首先要解决电池和用户行为的不可预测性。电池行为在很大程度上取决于条件，其中一些条件是不可预测的。一种可能的解决方案是基于直接测量和簿记系统两者结合的系统以增加适应性。自适应性SOC系统的基本原理如图3所示。

在系统中比较重要的是SOC的单位是库仑计数中的 [C]，因为确定了电池电流的时间积分。在 EMF 方法中，SOC是按百分比确定的，因此，库仑计在充电和放电状态下的含量也必须转化为百分比刻度。为此需要绝对规模的最大电池容量Capmax。必须考虑更新Capmax值的某些方法，以应对因老化造成的容量损失。

3 实验测试

本节将使用上一节中提出的系统和某款主流厂商电池来获得一些初步测试结果。主要研究不同负载条件和不同温度下估计的准确性。此外，还将研究放电期间发生负载变化时系统的行为，研究平衡状态下簿记系统的校准和容量更新机制。

3.1 实验条件设置

为了获得实验结果，共进行了两次实验。在每次实验之前和在每个温度下用标准方案初始化电池。该模式包括三个充放电循环，在 CC 模式下使用 500 mA 电流，在 CV 模式下使用4.1 V 电压，在充电模式下最小电流为 35 mA。电池以0.5C的速率放电至2.8V的电压。在充电和放电之间允许30分钟的中断时间。进行四次启动。

3.1.1 实验1条件设置

（1）查阅文献不足。很多大学有开设文献检索课，但是课程结束之后，能主动再查阅文献的学生比较少。针对某一个研究方向进行相关的检索总结就更少了。

充电方法与启动期间相同。在充电和放电之间允许有 30 分钟的中断时间。在以高于 0.15C 的速率放电至 2.8 V 后，中断 30 分钟，然后以 0.15 C 的速率再次放电至 2.8 V，然后再中断 30 分钟。这样做是为了确保电池电量耗尽。电池以 0.15 C、1.2C、2.8 C 的速率和定义的脉冲电流连续放电。

图3中，测量的电池变量I

、T

和V

是该模型的输入，矢量Ym包含了SOC，但也包含其他电池变量，例如电池串联电阻的估计值。另一种方案是基于I

和T

测量来估计电池电压，并将该估计值与测量值V

进行比较。该模型包含了函数f

和函数f

的组合。

分析模型中的新型消能减震复合墙板宽600 mm，高1000 mm，厚度120 mm，L型混凝土板翼缘高100 mm，翼缘厚120 mm，腹板高870 mm，腹板厚40 mm，复合墙板中防水保温材料厚40 mm。L型混凝土板的腹板内设置钢筋网单层配置φ6@100，翼缘配置φ8@80。耗能钢棒每根长120 mm，直径12 mm，间距为200 mm，钢棒距离L型混凝土板边缘100 mm，共配置两层，每层共3根耗能钢棒。如图1所示。混凝土板采用C30混凝土，纵筋采用HRB335钢筋，钢筋网采用HPB300钢筋，耗能钢棒采用HRB400钢筋。

基于直接测量系统的主要优点是不必一直连续连接到电池。一旦接入电池，之后可以直接从函数f

推断出SOC。该方法的主要难点在于确定函数f

，它应该描述在所有适用条件下测量的电池变量与SOC之间的关系。一般来说，实际使用中条件的变化量越大，基于直接测量的系统的准确度就越低。

在第二个实验中再次应用连续的充电和放电循环，间隔 30 分钟的中断时间。充电循环与第一个实验相同。对于以大于 0.15C 的速率放电至 2.8 V 的情况与上述相同。连续应用了三种不同的放电方式:

为制造业创造新的动能，关键是要努力创新。当前，全球制造业正在经历全方位的数字化转型，特别是工业互联网、工业云、人工智能等下一代信息网络技术的全面渗透。这极大地颠覆了原有的制造业。从生产方式上看，新型信息网络技术的综合应用使制造业现有的数字化、智能化、个性化、共享化和绿色化更加突出。随着传感器、工业软件、工业互联网和工业云等技术的日益普及，生产过程更加智能化，生产者满足个人需求的能力进一步增强。

1.以 I1=0.15 C-rate 放电 60 分钟，然后以 I2=2.8 C-rate，I2>I1 放电至 2.8 V。

㉜《北齐书》卷四《文宣纪》，第45页。据魏收本传，禅代诏册诸文皆为魏收所作。魏收用《伪古文尚书》之例，为程元敏先生所失检。

2.用 I2 放电 10 分钟，然后用 I1 放电至 2.8 V。

3.以 0.012 C 倍率 (10 mA) 放电 15 分钟，然后以 0.6 C 倍率放电 30 分钟，再以 0.012 C 倍率放电 30 分钟，最后以 0.6 C 倍率放电放电至 2.8 V。

3.2 实验结果

3.2.1 实验结果1

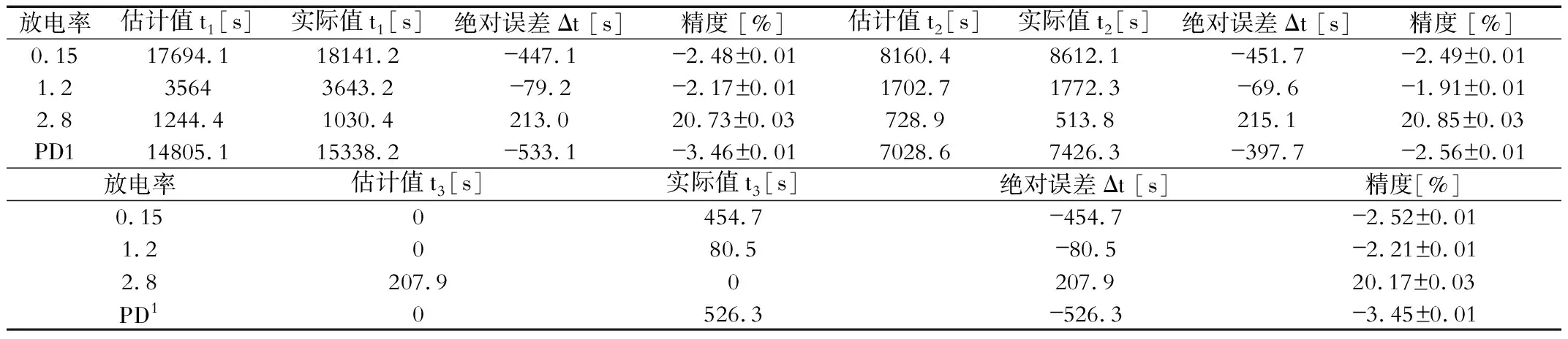
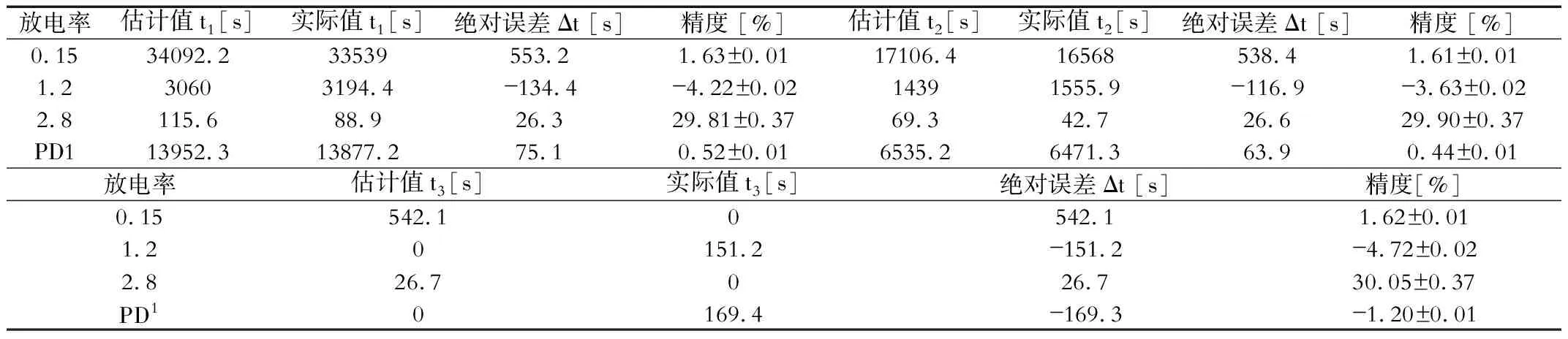
表1总结了实验1的结果。在主要放电条件下的剩余使用时间由算法在每次放电期间的三个时刻进行估计。将该估计时间与从那一刻到电池电压首次降至 2.8 V 以下的实际时间进行比较。选择第一时刻为施加放电电流的时刻。第二个时刻选择在放电中，最后一个时刻选择在估计或实际剩余使用时间为零时。估计时间少于 10 秒被视为零。误差

计算如下:

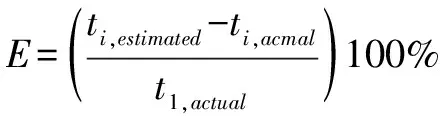
(Eq.1)

函数f

,其中 bk 表示簿记，V、I 和 T 是函数中的参数，基于库仑计数器的内容，即电流 I 随时间的积分。测量其他电池变量(V 和 T)以针对电池行为补偿库仑计数器的内容。 I本身的值也用于补偿计数器。

作为人才培养的输出机构，高职院校应把中职、高职学校的专业负责人、相关企业专家召集到一起，对中职升高职的专业人才培养方案进行分析比较，科学设计并有机整合，根据职业人才成长规律，按照知识与技能双螺旋上升的培养方式，实现中等职业教育到高等职业教育两个阶段培养目标的有机统一。

习近平重视社会教育，不断倡导全党学习、全民学习，建设学习型社会。习近平强调，中国“努力发展全民教育、终身教育，建设学习型社会，努力让每个孩子享有受教育的机会，努力让十三亿人民享有更好更公平的教育”[20]。习近平关心广大劳动者的职业成长和发展[21]，强调“构建网络化、数字化、个性化、终身化的教育体系，建设‘人人皆学、处处能学、时时可学’的学习型社会，培养大批创新人才，是人类共同面临的重大课题。 ”[22]因此，十九大报告指出，要“办好继续教育，加快建设学习型社会，大力提高国民素质”[1]。习近平对终身教育、终身学习、学习型社会的有关论述，为社会教育的蓬勃发展提供了科学指南。

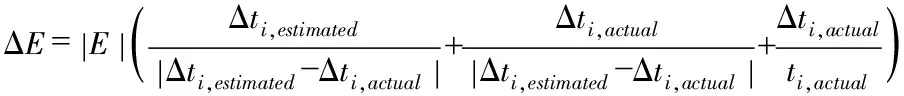
(Eq.2)

其中，Δ

,

和Δ

,

分别是可以确定估计和实际剩余使用时间的精度。假设 Δ

,

=Δ

1,

=Δ

。首先考虑 Δ

,

。这个时间是从

-

推断出来的，电池在

=

(

=

) 时是空的，

是进行估计的时间。时间温度是根据存储的 EMF 曲线和(等式1)的过电位函数在内部以高精度确定的。

在(等式1)的基础上，可以推导出以下表达式，用于确定

的精度Δ

。误差可以再次表示为

±Δ

:

实际剩余使用时间也可以从tempty-tp中找到。如上所述，临时指的是电池电压降至 2.8 V 以下的时刻，设备存储测量的电压值，当它们变化2 mV 时。由Vbat=2.8 V-2 mV 时确定tempty。假设放电曲线的斜率和以前一样为 0.04 mAh/mV，现在可以从 ((0.04 mAh/mV).2mV)/I 中找到以 [hr]表示的误差，其中 I 以 [mA]表示。现在可以从 (0.08 mAh/I).3600+0.06 中找到以 [s]表示的实际剩余使用时间 Δtactual 的总误差。

“梅陇镇击剑”是在二、三线城市人口集中的区域定期举办的击剑项目的竞赛与体验活动，旨在打造梅陇镇击剑项目品牌文化，带动全民健身发展，丰富群众休闲娱乐生活的需求，鼓励更多的人参与全民健身。例如，二三线城市承办国际性比赛，需要积极的宣传与参与人群的支持，而梅陇镇广场已经连续13年举办国际级击剑比赛，于2015年升级为国际A级赛事，并扩大了比赛规模。该赛事的成功在于打破了传统的体育活动组织，激发了群众观赏、感受、体验等行为活动。

3.2.2 实验结果2

表2总结了放电方案1和2的实验2的结果。这一次，选择第一个时刻作为放电电流变化的时刻，即在放电方式1中从 I1 到 I2，在放电方式 2 中从 I2 到 I1。改变电流(I2 在状态 1 和 I1 在状态 2)。第三个时刻被选择为估计时间或实际时间为零的时刻，估计时间小于10秒再次被视为零。

3.3 实验结果讨论

3.3.1 实验1结果

表1显示绝对误差 Δt 在整个放电时间内保持恒定。电池估计为空的时间不会改变，因此估计次数随着实际剩余使用时间减少。

通过表3可以确定，使用新算法获得的低温和大放电电流下的估计要好得多。

3.3.2 实验2结果

表2中显示的结果说明了在放电期间电流改变时，先前放电电流对SOC估计的影响。表2和3中给出的一些结果已包含在表4中，以进一步阐明这种影响。

表4显示，对于使用特定电流的局部放电，估计误差有所增加，但不会显着增加。例如，当电池在 25℃ 下以 0.15 C 的速率完全放电时，误差为 -2.52%。当电池首先以 2.8C 的大速率放电 10 分钟时，对于以 0.15 C 的速率进行局部放电，此误差会增加到 -4.46%。

本节的主要目的是研究在各种条件下(包括不断变化的负载条件)估计剩余使用时间的准确性。新算法SOC系统对低温下大电流放电的估计更好。尤其是在 0℃ 下以 2.8 C 倍率进行局部放电的估计具有可接受的准确度。当发生负载变化时，新算法SOC系统运行良好，因为完全放电和局部放电估计精度的差异是有限的。

4 结论

本文讨论了动力电池SOC的三种基本方法的主要特点和问题。直接测量系统涉及的主要问题是将所有可能的电池和使用条件包含在函数中，该函数将测量的电池变量与SOC联系起来。簿记系统的主要问题是定义可靠的校准时机，这些时机在电池使用过程中经常发生。

双优山葡萄施用本然土壤调理剂今年的营养生长、结果枝率、生育期影响虽然不突出，可能是第一年施用的原因，在以后的几年里，根据经验应该能有明显表现。今年试验结果在抗病性、增长性、可溶性固形物含量、出汁率、果梗率等多项性状上都优于施用化肥的。其中增长18.8%、可溶性固形物含量（手持折光仪测量）提高出12.2%。这对提高产量、提升品质的意义非常重大。土壤改良情况效果明显，施用本然土壤调理剂土壤通透性非常好，原来板结的土壤变得松软，效果非常明显。

本文提出并讨论了一种新的SOC系统，该系统结合了使用 EMF 方法的直接测量和使用过电位描述的簿记法，新的 SOC系统结合了两种方法的优点。使用新系统进行的一些初步测试结果表明，在包括负载变化在内的各种条件下的估计精度是较高的，与使用现有簿记系统获得的结果相比，新系统在大放电电流和低温下的估计更加优异。该方法为SOC状态估计提供了一种新的思路，对实际动力电池管理系统开发具有一定的借鉴作用。

[1]陆张浩,潘正军,许祥进.车用锂离子电池的SOC估算方法研究现状[J].时代汽车,2021(06):161-162.

[2]熊鑫.车用锂离子电池联合状态估算方法研究[D].西南科技大学,2020.DOI:10.27415/d.cnki.gxngc.2020.001079.

[3]肖业,刘芳,刘欣怡,林辉.电动汽车动力电池健康状态在线动态估算方法[J].电源技术,2021,45(02):177-180+235.

[4]雷钧.电动汽车动力电池剩余电量的常用估算方法[J].机械工程与自动化,2020(06):178-180.

[5]ChristopherD.Rahn&Chao-Yang Wang. 电池建模与电池管理系统设计[M]. 1. 机械工业出版社, 2021.4.