突然释放型浊流在不同坡折渠道中的流动与沉积

季雪瓜，陶丽云，黄河清

安徽工业大学环境流体研究所，安徽马鞍山 243000

0 引言

浊流（turbidity currents）是含泥沙水体在重力作用下沿水下斜坡流动的重力流[1]。非稳定沉积体在外力作用下的水下滑坡可形成突然释放型浊流（sudden-release TC），其流动及沉积特性为海洋地质学、海底油气勘探与开采以及海底灾害防护等关注的重点[2-8]。如鄂尔多斯盆地和加利福尼亚文图拉盆地产生的浊流沉积均与海底油气的形成和储集有着密切关系[9-10]。

海底浊流发生的突然性和其对观察设备的破坏性使得野外直接观察浊流的流动较为困难，只测得了少量的海底浊流的流动速度及浓度分布[11-13]，更多的是对其沉积特性的观察与描述：通过对沉积的形态、岩相及构造等特点分析得到海底沉积扇相模式，认识到海底峡谷是陆源沉积物向洋底搬运的重要通道，且浊流在其流动过程中会重塑陆架边缘及海底沉积地貌[14-19]。

早期的突然释放型重力流实验研究多为水平渠道上的闸门释放型盐水流，探讨了重力流在水平渠道中滑塌的动力学机理以及其头部运行速度与环境流体卷吸（entrainment）之间的关系，并详细描述了其头部形态以及K-H 涡等[20]。近期水平渠道上闸门释放型单粒径与多粒径颗粒的浊流研究表明：砂体发育的规模与其坡度、高度差及流速外界条件有关，高差大、坡度较陡及水位越高，浊流的水动力就比较大，形成的沉积砂体范围和厚度则越大；混合粒径要比单一粒径向前流动的距离要远，沉积厚度在上下游呈现不同的形态分布[21-26]。

随着计算机硬件及计算技术的迅猛发展，浊流的数值模拟取得了丰硕的研究成果。现阶段浊流的直接数值模拟（DNS）及大涡模拟（LES）主要集中在低至中雷诺数（Re≈2 000~200 000）的实验室尺度且水平突然释放型重力流的模拟上，值得注意的是二维LES 重力流浊流头部及和环境流体界面处的Kelvin-Helmholtz 渦比实验显示的过分发展，需要三维的LES 才能获得更加接近实验观察的涡动[27-32]。尽管雷诺平均（RANS）模型在揭示重力流机理和湍流涡动方面有所不足，但却能较好地再现实验室尺度下突然释放型和连续入流型的多种盐水重力流及浊流的厚度、深度平均浓度、头部运行速度等以及单粒径至多粒径浊流的沉积特性等[33-38]，并且也在中至大尺度海底浊流的模拟中取得了与实验观察接近的流动及沉积特征[39-40]。

最新的关于连续入流的重力流研究显示，坡度对重力流的流动起着显著的控制作用[41]，坡度对突然释放型浊流流动及沉积影响的研究尚且不足。本研究拟通过模拟等量的突然释放型浊流在1°~10°不同坡折渠道中的流动与沉积，探索坡度对突然释放型浊流的控制作用。

1 数学模型及其边界条件

模拟对象为采用布辛尼斯克假设的低密度突然释放型浊流，浊流和环境流体一起可看作不可压缩流体，应用如下雷诺平均后的质量及动量方程[35]：

式中：Ui是xi方向上的雷诺平均速度分量；P为雷诺平均压力；ρ、ρ0分别为浊流及其环境流体密度；gi是重力加速度；涡黏度νt通过浮力项修正的湍流k⁃ε模型确定[34-35]。对于分选差的低密度浊流沉积物，将其分成k个粒径组并假设其随环境流体一同运动的同时在重力方向上有一自由沉降速度Vsk来模拟。

式中：Ck是k粒径组沉积物的体积比浓度；δj2是克罗内克数；Sc是施密特数，本研究中取其值为1。

图1是本研究模拟等量浊流在斜坡上方的闸门释放后沿斜坡及经过波折渠道的流动与沉积的二维渠道示意图。左右边界均设定固体墙面，模拟一定时长的浊流流动，在其流至右边墙面前停止，以防止墙面反射的影响。上部水面作对称界面处理，底部边界对流场应用固体边界的墙面律，假设其粗糙度为入流沉积物的平均粒径，同时以如下的Exner方程（式4）综合考虑各粒径组颗粒的如等号右边第1~3项所分别代表的推移质搬运、沉降及夹带所引起的底部边界的变化[35]。

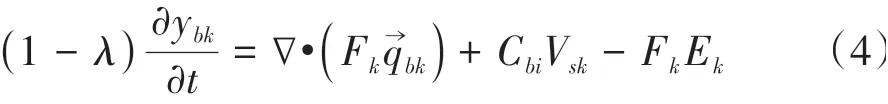
式中：λ为河床物质孔隙率；yb为底床高度，下标b表示和底床相关的量；推移质搬运通量qb及沉积物的夹带系数E采用文献[35，42]的经验公式计算；Fk为k粒径组颗粒在混合层内部的的体积分量，关于模型的详细介绍及各参数的取值与计算请参见模型提出文献[35]。该模型较好地取得了和二维坡折渠道上的具连续入流的浊流实验、水平渠道上的突然释放型浊流实验以及浊流在三维直渠道、弯道渠道内流动及沉积的较为一致的模拟结果[35-37]。

2 模拟网格及初始条的设定

按原型1∶100 的比例缩小的带坡折的突然释放型浊流在二维渠道内流动的模拟设定如图1 所示。第一段闸门后左边2.25 m×1 m 的水平段是初始密度为ρ1的浊流混合悬浮液。其内所含沉积物的比重设为2.65，总体积比浓度为2%，如表1所示，5种不同粒径按由小至大的顺序含量分别为10%、20%、40%、20%和10%。粒径的选择考量了其自由沉降速度满足密度弗雷德数准则[43-44]。紧接着水平坡的后面为水平长度6 m的斜坡连接至一段长度为60 m的水平底坡。

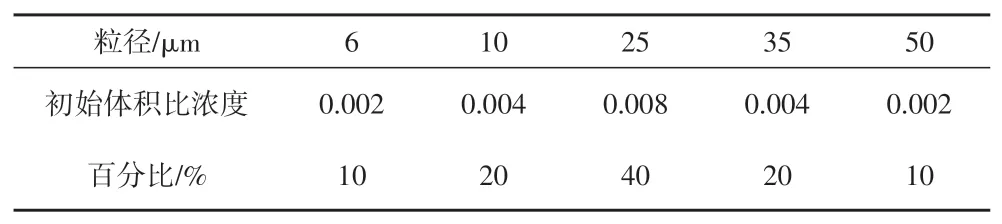
表1 初始混合悬浮液中的不均匀沉积物粒径设定Table 1 Preset value of uneven sediment particles in the initial mixed suspension

图1 模拟空间示意图（ρ1 表示初始浊流密度；ρ0 表示环境流体密度，θ 为可变坡坡度）Fig.1 Geometric diagram (ρ1: density of the initial turbidity current; ρ0: density of the environmental fluid ;θ: angle of the slope bed)

将研究等量的突然释放浊流在1°、3°、7°、10°四种不同坡折上的流动及沉积。主要通过第一次浊流事件来观察流动特征，通过重复六次等量的突然释放型浊流来模拟自然界多发性浊流事件。每次模拟时长为400 s，其时初始浊流中的沉积物大部分已沉积完毕且可以有效防止墙面反射的影响。

由自主开发软件SIMUSOFT 所智能生成3°坡折网格前30 m如图2所示，网格密度为600×60，在浊流流动的底部及2个坡折处都自动加密等比扩展，以捕捉到对应处速度及浓度的较大梯度变化。对低（400×40）、中（600×60）及高（900×90）三种密度网格进行了模拟验证。对比观察60 s 时密度云图可见（图3a~c），低密度网格所模拟的浊流流动速度及形态已经和中等密度网格的非常接近，但中等密度网格所模拟的在头部后边的涡形态更接近于高密度网格的；并且，此时由中高密度网格模拟所获得的X=8.25 m 处的断面速度和浓度（图3d，e）更加接近，可认为中密度网格的模拟接近收敛，适用于本研究。

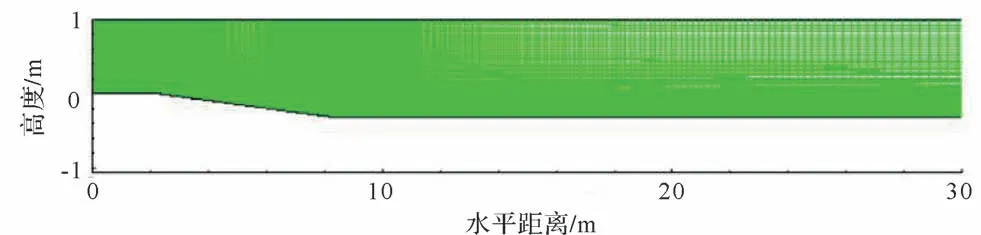
图2 3°坡折突然释放型浊流数值模拟用网格Fig.2 Grid for 3°slope break numerical simulation of a sudden￣release turbidity current

图3 低、中、高三种不同密度网格模拟突然释放型浊流在释放后60 s 时密度云图对比(a~c)及X=8.25 m 处的断面浓度（图d）和断面速度（图e）对比Fig.3 Density cloud comparison 60 s after release (a￣c); 8.25 m cross￣sectional concentration(d) and velocity (e) from three different grids

3 模拟结果与讨论

本节通过对比突然释放型浊流在1°、3°、7°和10°四种不同坡折渠道上的密度云图、典型剖面浓度、速度以及它们的深度平均量来分析坡度对流动的控制作用，并通过六次浊流事件后的沉积特征分析坡度对沉积的影响。

3.1 密度云图

等量的（2.25 m×1.0 m）突然释放型浊流释放至坡折分别为1°、3°、7°和10°的渠道后在20 s、40 s、100 s 时的密度云如图4 所示，在斜坡为1°~10°的范围内：浊流头部运行速度与浊流头部高度及上部的卷吸涡随着坡度的增加而增加（图4a，b），这和Gladstoneet al.[23-24]在水平渠道内所观察的流量或浓度增加的浊流实验现象类似。同时我们也观察到另一个现象，即浊流速度并不是与坡度的增加呈线性增加，其头部速度的增加有着逐渐减缓的趋势，反映了突然释放性浊流和连续入流型的浊流类似，其环境流体的卷吸（entrainment）也是随着坡度的增加而增加[45]，进而会带来阻力的增加，致使浊流头部运行速度随底坡增加的速率减缓。浊流释放后40 s时的浓度云图（图4b）显示，越靠近底部及头部，浊流的密度越高；并且，由于大坡折浊流具有相对较强的卷吸作用，其头部的浓度衰减则更快（图4c）。

3.2 断面速度和浓度

对比浊流释放后40 s（图4b）三个不同断面X=1.25 m（初始段）、X=5.25 m(斜坡段)、X=8.25 m（坡折处）浊流断面速度和浓度图（图5）可见：坡上水平段浊流浓度及速度均衰减快，表明只要有斜坡提供浊流，不论斜坡大小，40 s 后浓度及速度都衰减至很小（图5a），这点和连续入流浊流有很大不同[33-35,43-44]；浊流头部经过后的尾部的坡上（图5b）及波折处（图5c）垂向断面速度分布和连续入流的浊流类似，在离底部不远处有一极大值，反映了两种不同启动机理（连续注入和突然释放型）的浊流在流动上的本质类似之处，即最大速度之下为壁面剪切层、之上为混合层剪切区[2￣3,38]；垂向断面的最大速度随着坡度的增加而增加；垂向断面上存在浓度的密度分层，特别是在底部断面最大流速之下的壁面剪切层内，浓度梯度大；坡度越大，浊流断面浓度相对较低，反映了浊流卷吸作用随着坡度的增加而增强。

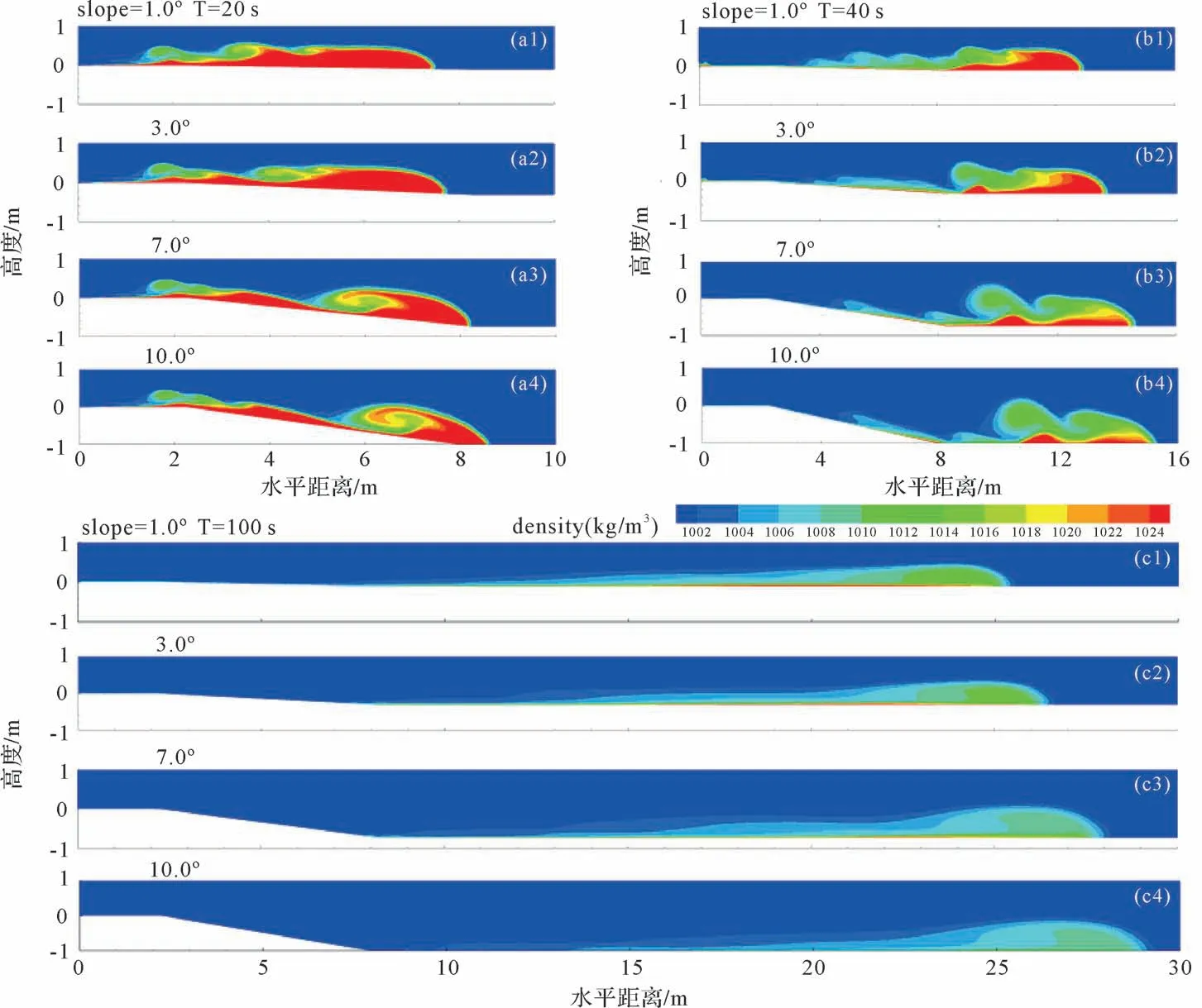
图4 等量突然释放浊流在4 不同坡折底坡上的20 s（a）、40 s（b）及100 s（c）时的密度云图Fig.4 Density contours of equal￣volume turbidity currents passing 4 different slope breaks at 20 s (a), 40 s (b), and 100 s (c)

图5 不同坡折渠道上浊流突然释放后40 s 时在初始段（a，X=1.25 m）、斜坡上（b，X=5.25 m）及波折处（c，X=8.25 m）处的的断面浓度及速度对比图Fig.5 Concentration and velocity comparison of turbidity currents 40 s after sudden￣release via 4 different slope breaks at three different cross￣sections

3.3 深度平均厚度、速度及浓度

浊流在流动过程中不断地携带环境流体，使浊流与外界没有清晰的分界点，研究者多采用如式5~7所定义的重力流厚度h，深度平均速度-U及深度平均浓度-C来描述浊流[2￣3,38,46]。

式中：U表示浊流的水平速度，C表示浊流的体积浓度，y为垂直于主流向的方向。

突然释放型浊流在不同坡折上释放后100 s 时的厚度、深度平均速度及浓度如图6 所示。可以看出，单个浊流的头部最厚，浊流的厚度随着坡折的增大而增大，但在7度以后增加不明显（图6a）；深度平均浓度（图6b）和连续入流型的[43-44]恰相反，头部最高，向尾部接近于线性地下降，坡折影响不明显；另一个特点为坡折小的整体浓度高、坡折大的整体低，这是因为坡度高卷吸强，和图4c的观察一致；单次浊流的深度平均速度形态和深度平均浓度类似，头部高，由头部至尾部近似线性下降（图6c）。

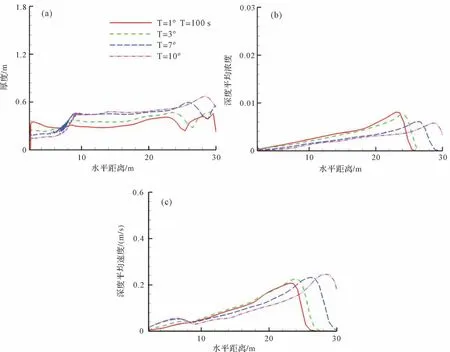
图6 不同坡折渠道上浊流突然释放后100 s 时的厚度（a）、深度平均浓度（b）及深度平均速度（c）Fig.6 The thickness (a), depth￣averaged concentration (b), and velocity (c) of turbidity currents 100 s after sudden￣release via 4 different slope breaks

3.4 多浊流事件后的沉积厚度及粒径分布

在1°、3°、7°和10°坡折渠道上都重复进行了6次等体积浊流突然释放400 s 模拟，通过方程4 跟踪记录底床的高度及粒径分布，最后得到浊流在不同波折渠道上的沉积或侵蚀沉积物粒径分布云如图7所示。

可以看出，小坡折（1°、3°）处产生大量沉积，沉积最厚处出现在离坡折不远的下游，其后沉积厚度近线性减小或略呈上凹形；小坡折渠道上沉积的平均粒径上下游差别不大，几近平均粒径，沉积隆起最高处附近稍大些，隐约可见各次浊流沉积底部颗粒大上面小的沉积纹理。大坡折（7°、10°）处有一定的侵蚀，坡折愈大、侵蚀越多，其后才开始大量沉积，其形态和小坡折不同的是呈上拱状，最厚处出现在离坡折更远处（图7d）；大坡折浊流沉积的平均粒径分布和小坡折不同之处为上游的较大，往下游逐渐减小，在沉积隆起的各次浊流沉积底部颗粒大、上面小的沉积纹理比小波折的更加清晰明显。

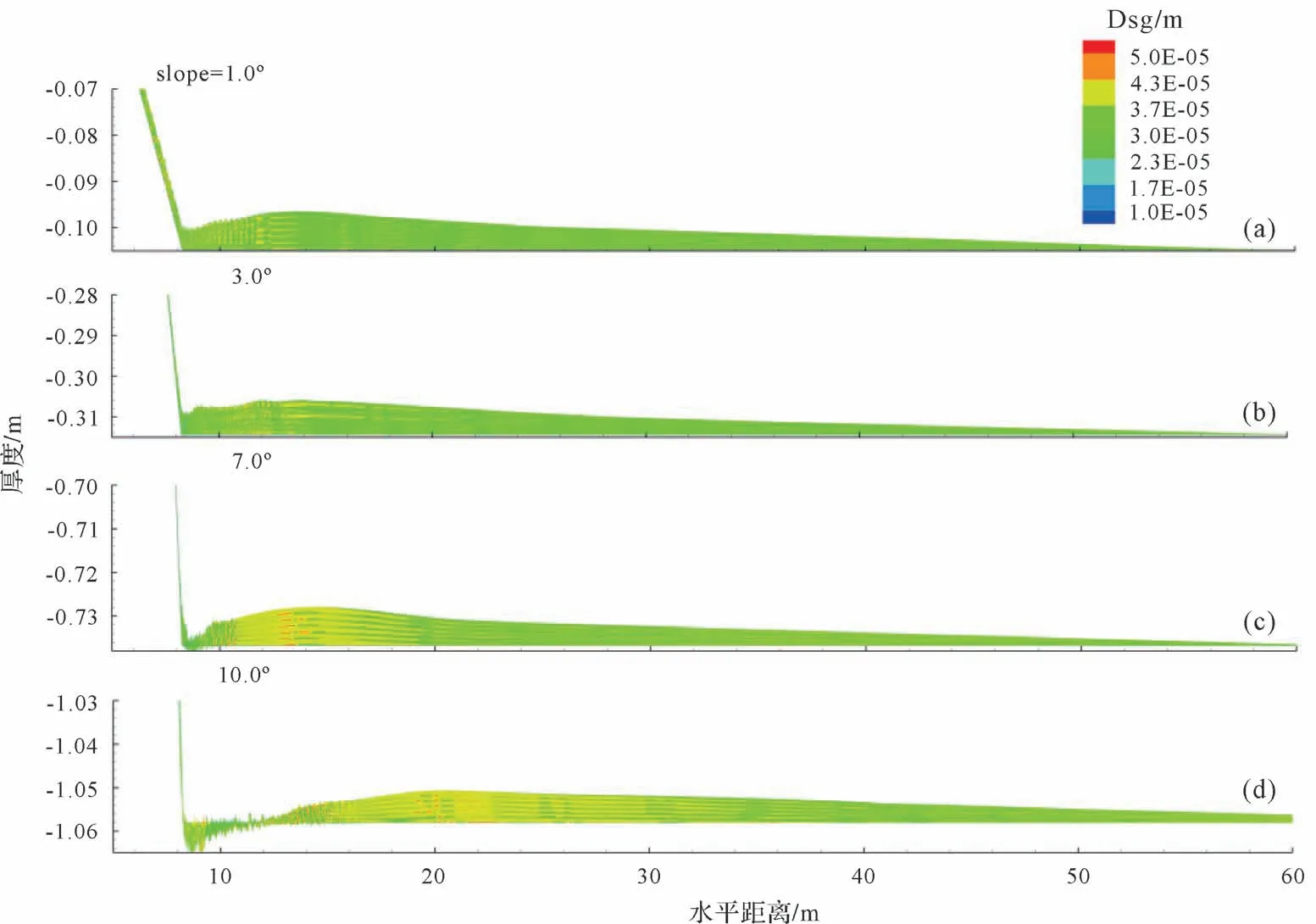
图7 不同坡折渠道上6 次等量突然释放浊流事件的沉积或侵蚀厚度及平均粒径云图Fig.7 The average particle diameter deposit contours for six runs of equal￣volume sudden￣release turbidity currents on different slope breaks

4 结论

本研究应用雷诺平均纳维尔—斯托克斯模型对低密度等量突然释放型浊流在不同坡折渠道内的流动进行了二维数值模拟，得出如下主要结论：

（1）突然释放型浊流的流动速度随着底坡坡度的增加而增加，但随着坡度增大因增强了对环境流体的卷吸作用而减缓了其速度增长率。

（2）突然释放型浊流的垂向断面速度和浓度分布与连续入流型浊流有着较高的类似，速度在靠近底部处存在一个最大值，浓度在底部最大，往上指数式地下降，反映了两种入流机制的浊流在受到底部边界层及上部混合层作用方面的一致性。

（3）突然释放型浊流的厚度、速度及浓度和连续入流的对比有很大的不同。突然释放型浊流厚度在头部最厚，随着坡度的增加而增加，深度平均速度和浓度形态非常相似，均是头部最大且向尾部呈线性下降。

（4）突然释放型浊流的沉积形态在小、大坡折上明显不同。小坡折（1°，3°）上在坡折处产生沉积，沉积最厚处离坡折处不远且上下游平均粒径相差不大；而大坡折（7°，10°）在坡折处遭受侵蚀，随着坡度的增大侵蚀增加，沉积最厚处离坡折处较远且上游平均粒径较下游的明显大。从厚度上观察浊流沉积由最厚处至下游的沉积形态，小坡折呈线性减小或接近上凹形，而大坡折呈上拱状。