基于航迹关联的抗角闪烁跟踪算法研究

闫晶一，于 勇，张 彬，韩 伟，张剑琦

（北京遥测技术研究所 北京 100076）

引 言

高分辨雷达与分布式目标距离较近且相对速度较大时，目标角闪烁是雷达平台跟踪目标时的主要误差来源，会导致无法稳定跟踪目标，甚至可能会导致跟踪点偏离目标。当雷达和目标相对距离较大时，复杂目标可看作理想点目标，散射回波为球面波，雷达天线中心可以精确地指向目标；当雷达和目标相对距离较小时，复杂目标可看作由多个强散射点组成的分布式目标，散射回波为多个子回波的矢量合成，波前产生畸变，雷达天线中心指向的位置不断变化，从而导致雷达平台无法稳定跟踪目标[1]，这种现象称为“角闪烁”。对角闪烁抑制算法的研究有助于高分辨雷达跟踪精度的提高。

角闪烁抑制问题是国内外研究的热点，抑制方法大致分为三类：较为广泛应用的一种方法是利用高分辨技术抑制角闪烁，如基于距离高分辨[2]和频域高分辨的单脉冲测角方法等；还可以根据不同的雷达体制和应用背景，采用分集（空间、频率和极化）方法接收目标的散射回波，并通过加权平均处理抑制角闪烁；最后一种是应用一些信号处理和跟踪滤波方法[3]，通过对目标位置进行预估，从而减少角闪烁的影响。

经研究，角闪烁噪声呈现出长拖尾、非高斯的特性[4]。而针对拥有这种特性的噪声，标准卡尔曼滤波的性能将大大下降。扩展卡尔曼滤波[15]可用于跟踪非线性目标，但是它适用于跟踪单目标，对于分布式目标效果并不理想。

基于此，本文提出一种基于航迹关联的抗角闪烁跟踪算法，即应用联合集成概率数据互联算法[5]JIPDA（Joint Integrated Probabilistic Data Association Algorithm）进行跟踪。由于此算法需要枚举所有的联合航迹-观测分配事件，该事件的数目随目标和观测的数目增长而呈组合爆炸式增长，使得算法在计算上复杂度太高，因此本文将强散射点的幅度特征与JIPDA 算法相结合，在成功提高了高分辨雷达在角闪烁背景下对分布式目标的精准跟踪能力的同时，有效降低了计算量。

1 分布式目标的散射中心模型

当高分辨雷达对目标进行近距离跟踪时，形状复杂的目标可以看作由多个强散射点组成[4]，用分布式目标模型对其进行描述，示意图如图1 所示。各散射中心对雷达发射信号进行延时和调幅后，形成的各子回波求矢量和即为目标回波。

图1 分布式目标的散射中心示意图Fig.1 Diagram of the scattering center of a distributed target

设雷达发射信号为

如果目标在快时间内相对于雷达平台姿态不变，目标回波信号为：

式中，M为散射中心个数，F X（θ）表示同一平面上的天线方向性函数，若X=Σ 则代表单脉冲天线和波束，X=Δ 则代表差波束；θk为第k个散射中心的角度，σk为散射强度，为回波延迟。

2 单脉冲和差比幅测角原理

在方位和俯仰任一平面上，比幅单脉冲测角法通过比较和、差波束收到的目标信号强度来估计出目标偏离等信号轴的角度信息[6]。利用和通道信号对差通道信号进行归一化处理，再取实部，可以得到强散射点的角度估计，即单脉冲角度测量公式为[7]：

其中，K为差波束天线方向图在0°的斜率，A为和波束天线增益。sΣ（t）和sΔ（t）分别代表和、差波束收到的关于某强散射点的目标回波信号。

3 基于航迹关联的抗角闪烁跟踪算法

3.1 单脉冲雷达角度跟踪算法

单脉冲雷达角度信息处理跟踪流程如图2 所示。先对目标的三通道回波进行距离徙动校正，脉冲压缩匹配滤波和相参积累处理，然后在和通道的高分辨一维距离向上，实现对幅度超过检测门限的目标强散射点的检测。将检测到的强散射点按幅度排序，并根据单脉冲比幅测角算法求出其方位角和俯仰角。为降低多目标跟踪滤波算法JIPDA的计算量，每帧仅选取能量最强的N个事件构成联合分配事件空间[14]，并将选中的强散射点距离和角度测量数据一起输出，最后利用这些信息，应用联合集成概率数据互联算法对目标进行跟踪。

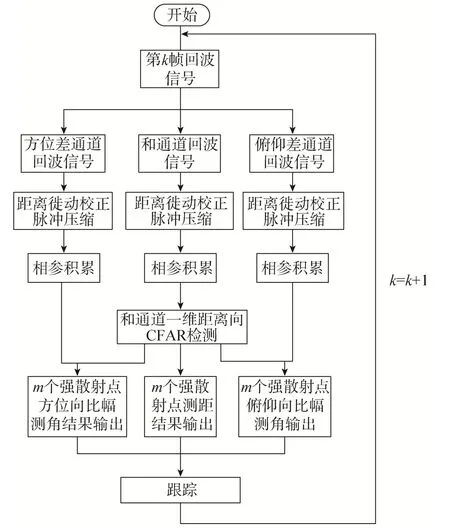
图2 单脉冲雷达角度信息处理跟踪流程框图Fig.2 Flow chart of Angle information processing and tracking of monopulse radar seeker

3.2 联合集成概率数据互联算法

联合集成概率数据互联算法是一种全邻算法，适用于多目标环境下[10]，可以在航迹邻近或者航迹交叉情况下对多目标进行数据关联，可以形成多条航迹，在过程中可以将杂波过滤掉，并且对分布式目标上的不同强点形成不同的航迹[11]，从而选一条航迹进行稳定跟踪。

在航迹不断更新的过程中，航迹的存在性需要一个量作为度量，这个量可以决定航迹是否延续以及延续航迹的目标点的选择。大多数跟踪情况下，每条现有航迹对应的潜在目标的存在性是一个随机事件。所以本文引入目标存在性作为航迹的一个状态分量，用它的概率作为航迹质量的度量。

本文使用马尔可夫链一模型作为目标存在性演化模型，目标或是存在，或是不存在，如果目标存在，它的观测以检测概率PD出现。目标存在性概率的演化公式为[12]：

图3 JIPDA 算法流程图Fig.3 JIPDA algorithm flow chart

①航迹状态预测

目标存在性的演化过程遵循马尔科夫链一模型[9]，则对第k帧的目标存在性预测为：

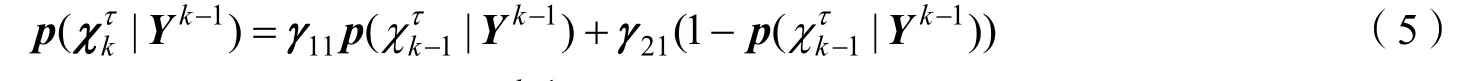
第k帧的目标航迹状态的预测值可根据目标的运动方程进行预测：

② 观测选择

利用式（6）和式（7）进行预测得到目标观测 yk(i)的位置观测概率密度[8]：

若观测 yk(i)满足上式，则认为此观测是这条航迹的一个观测，似然函数依据文献[9]可以得到如下表示

若观测不满足式（9），说明此观测未被这条航迹选中，即此观测关于这条航迹的似然函数为0。对所有的观测重复上述步骤，最终得到这条航迹选择的观测集合。

③数据关联

记k时刻航迹τ预选观测的似然比为

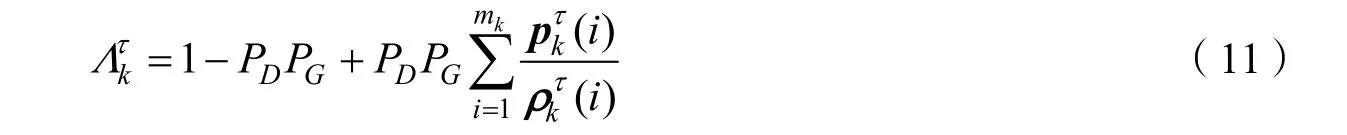
输出的目标存在性后验概率由下式给出

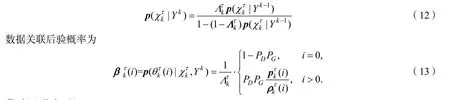
④ 航迹状态更新

本文通过标准KF 方法更新航迹状态[13]

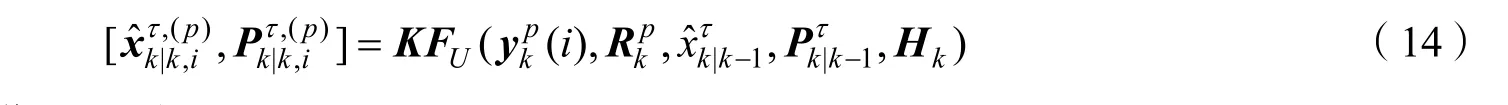
依次对航迹τ选择的mk个观测进行上述步骤运算，得到mk个更新后的轨迹状态分量，最终通过高斯混合，得到输出的第k帧航迹状态的后验概率密度的均值和协方差矩阵为

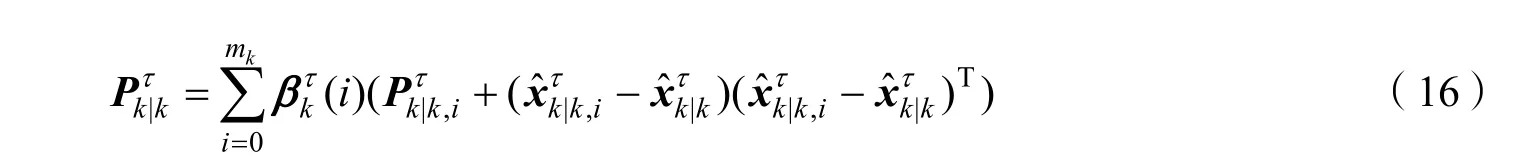
经过对航迹状态进行更新后，之前的航迹实现了选择和延续，将第k帧时输出的目标存在性的后验概率和航迹状态的后验概率密度作为第k+1 帧进入跟踪的输入。

3.3 算法计算复杂度分析

跟踪前信号处理的计算复杂度为：

式中，Im表示复数乘法，Ia表示复数加法，相参积累回波脉冲数为M，距离采样点数为Nr个。联合集成概率数据互联算法是一种集成算法，它的计算复杂度为：

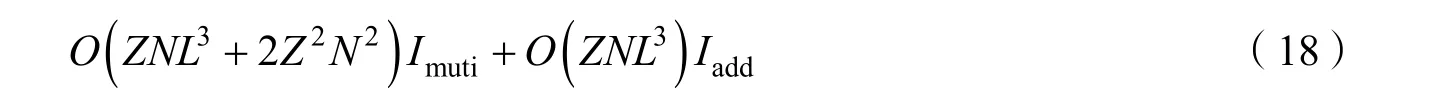
其中L为状态方程维数，Z为当前航迹条数，N为当前检测到的点数，Imuti为实数乘法，Iadd为实数加法。本文中L=9，M5≤，N5≤，此计算复杂度是所有步骤都基于计算量最大的分支下得到的，实际处理中，运算量小于此值。

4 仿真实验

首先利用仿真实验对目标角闪烁进行说明。仿真参数为：舰长160 m，舰宽15 m，飞行甲板最宽37 m，擦地角范围为60°～70°，飞机速度为200 m/s，距离范围为5.8 km～6.3 km。仿真舰船强散射点分布如图4所示，其中，最强点分别在船头和船中后侧多个散射点聚集处。

图4 舰船模型俯视图Fig.4 Top view of ship model

角闪烁背景下，若不采用角闪烁抑制策略，只依据最强点跟踪，距离跟踪曲线如图5 所示，从中可以看出，由于角闪烁问题，最强散射点的不断变化会导致无法稳定跟踪，甚至可能会导致跟踪方向偏离目标。

图5 角闪烁背景下最强点距离跟踪曲线Fig.5 Distance tracking curve of the strongest point under angular scintillation background

随后，利用实测数据来验证本文所提出的算法，仿真所用的实测数据来自于某Ku 波段雷达对杂波背景下舰船目标的探测跟踪，此舰船最强的两个散射点分别在船头和船尾，雷达系统的部分参数见表1 所示。

表1 舰船目标跟踪参数Table 1 Ship target tracking parameters

此时飞机沿X 轴方向以约100 m/s 的速度飞行，截取的数据为擦地角60°～69°部分。仿真结果如下：

对不同擦地角的原始数据进行匹配滤波及相参处理，得到图6 和图7。图6 为擦地角为44°，雷达平台与舰船目标距离为6 500 m 时的强散射点检测结果，图7 为擦地角为62°，雷达平台与舰船目标距离为4 530 m 时的强散射点检测结果。从图中可以看出，擦地角超过60°时一维距离像中有多个强散射点，出现了角闪烁现象。

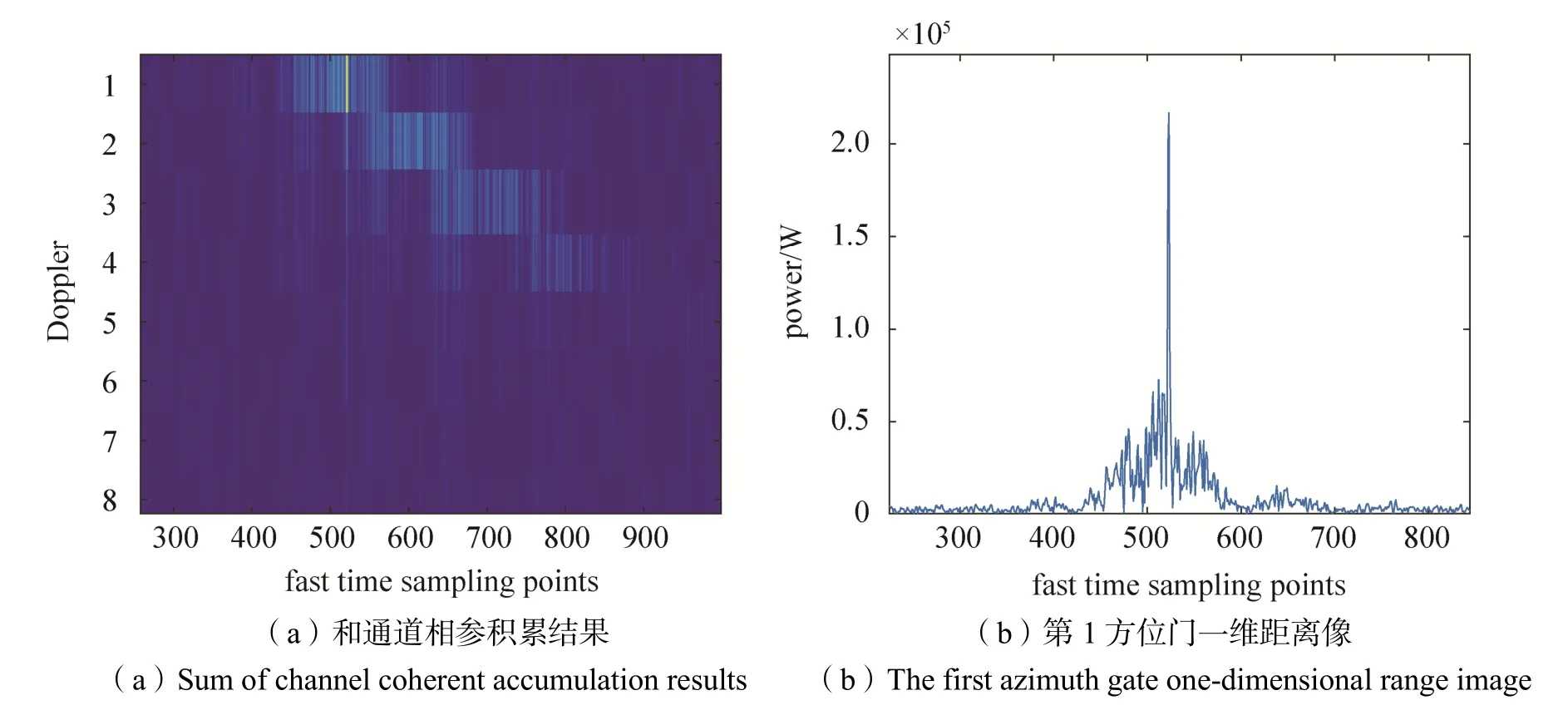
图6 擦地角42°时强散射点检测结果Fig.6 Detection results of strong scattering points at 42° Angle

图7 擦地角62°时强散射点检测结果Fig.7 Detection results of strong scattering points at 62° Angle

每帧回波数据经过高分辨雷达一维距离向检测算法处理后，取其中幅度最强的5 个散射点，分别用EKF 和JIPDA 算法处理。图8（a）为EKF 算法进行跟踪时，EKF 算法跟踪曲线、最强散射点的距离跟踪曲线和理论距离跟踪曲线对比图，从中可以看出经过EKF 后，跟踪曲线变得较为平滑，但是跟踪距离曲线有较大的起伏，在不同的强点之间跳跃，针对分布式目标情况下的角闪烁抑制的效果不够理想。图8（b）为JIPDA 算法与EKF 算法距离跟踪效果对比图，图8（c）为JIPDA 算法与EKF 算法距离误差曲线对比图。从中可以看出，经过JIPDA 算法处理后，跟踪曲线形成了船头和船尾两条距离误差稳定的航迹，可以选择其中一条航迹进行稳定的跟踪。

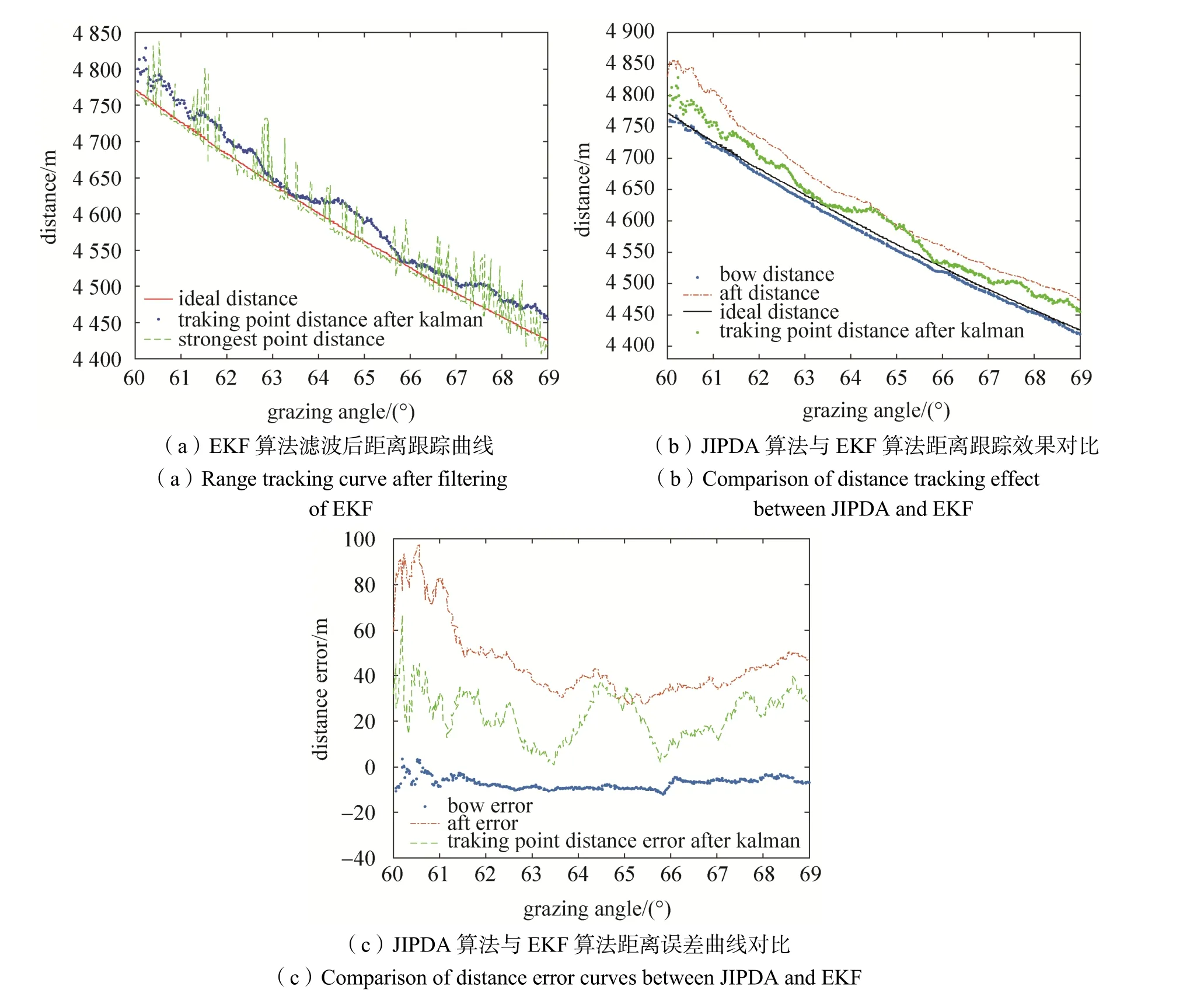
图8 JIPDA 与EKF 算法距离跟踪性能比较Fig.8 Comparison of range tracking performance between JIPDA and EKF algorithm

图9 为JIPDA 与EKF 算法方位角跟踪性能比较结果，图10 为JIPDA 与EKF 算法俯仰角跟踪性能比较，从图中可以看出，EKF 算法处理后的航迹曲线起伏较快，JIPDA 算法处理后的航迹曲线起伏较缓，且在相应惯导角度曲线附近具有随机起伏，与相应惯导曲线基本吻合。

图9 JIPDA 与EKF 算法方位角跟踪性能比较Fig.9 Comparison of azimuth tracking performance between JIPDA and EKF algorithm

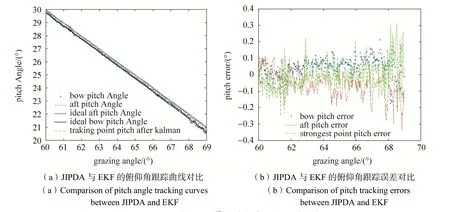
图10 JIPDA 与EKF 算法俯仰角跟踪性能比较Fig.10 Comparison of pitch angle tracking performance between JIPDA and EKF algorithms

5 结束语

针对高分辨雷达近距离跟踪目标时的角闪烁问题，本文提出了一种基于航迹关联的抗角闪烁跟踪算法，将强散射点的幅度特征与JIPDA 算法相结合，对分布式目标进行跟踪，并通过对实测的Ku 波段回波数据中擦地角为60°～69°部分进行处理，得到了两条航迹，均可以实现较稳定的跟踪，针对分布式目标的跟踪效果好于扩展卡尔曼跟踪算法。结果证明该方法能够提高雷达平台近距离跟踪阶段对分布式目标的精准跟踪能力，具有广阔的应用前景。