基于投影矩阵搜索的相干源DOA 估计算法*
宗佳虹,戴旭初
(中国科学技术大学 电子工程与信息科学系 合肥 230027)
引 言
波达方向(DOA)估计是阵列信号处理的研究热点,在雷达[1]、导航[2]等领域具有广泛的应用前景。传统的DOA 估计算法中,多重信号分类算法MUSIC[3]、旋转不变子空间算法ESPRIT[4]等子空间类算法具有良好的估计性能和超分辨能力,但是对于相干源,阵列输出信号的协方差矩阵的秩亏缺导致子空间估计错误,从而使算法失效[5,6]。
针对相干源DOA 估计问题,许多学者提出了解相干算法,例如空间平滑法[7,8]、Toeplitz 矩阵重构法[9]、基于SVD 的解相干算法[10]等。文献[7]提出的空间平滑算法具有良好的解相干性能,且计算量小,被广泛应用于实际工程中。但是,空间平滑算法存在阵列孔径的损失,从而降低估计的分辨率与精度,特别是,空间平滑算法只适合于特殊阵列,即需要子阵列结构具有移不变性,例如均匀线阵。
对于一般的阵列,可以考虑采用虚拟内插变换法[11,12]将其变换为均匀阵列,再进行空间平滑等解相干处理。虚拟内插变换是在某扇区范围内进行内插,将原阵列变换为一个虚拟阵列。不过,虚拟阵列变换只能针对某一入射角范围,且会引入额外的误差,内插范围越大,变换误差越大,从而导致DOA 估计性能降低。
针对上述问题,本文提出了一种基于投影矩阵搜索的DOA 估计算法,其基本思想是由阵列流型导出噪声子空间的投影矩阵,将接收信号样本投影到噪声子空间,获得空间谱,进而得到相干源的DOA估计。该算法适用于任意阵列结构(如非均匀线阵),且无需进行虚拟内插、空间平滑等预处理,避免了变换误差和孔径损失,具有良好的估计性能。
1 信号模型
考虑K个远场窄带平稳信号入射到空间某窄带阵列上,设阵列的阵元数为M(M>K),信号中心频率为ω,第m个阵元在时刻t的输出信号可表示为:

其中,si(t)为第i个窄带源信号,θi为第i个信源到达阵列的入射角,τm(θi)为第i个源信号到达第m个阵元时相对于参考阵元的时延,v m(t)为第m个阵元的加性噪声,其功率为σ2。将M个阵元t时刻的接收信号表示成矢量形式,则有:


设快拍数为N,则接收到的N个信号样本用矩阵形式可表示为:

其中,X=[x(t1),…,x(tN)],S=[s(t1),…,s(tN)],V=[v(t1),…,v(tN)]。
定义阵列接收信号的协方差矩阵为:

其中,λi和ui分别为R的第i个特征向量和特征值,且M个特征值满足如下关系:
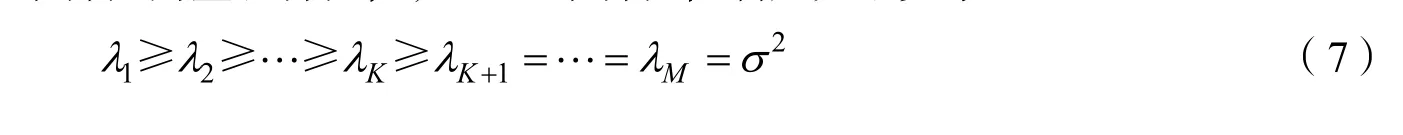
基于特征空间理论,Us=[u1,u2,…,uK]构成了接收信号的信号子空间,Un=[uK+1,uK+2,…,uM]构成了接收信号的噪声子空间,且Us与Un正交。子空间类算法就是利用该正交性进行DOA 估计,因此传统的子空间类算法需要对子空间进行准确的估计。
实际应用环境中,源信号之间可能是相关或相干的。设两平稳信号si(t)、s k(t),其相关系数定义为:

由Schwartz 不等式可知|ρik| ≤ 1,当|ρik|=0时,称si(t)与s k(t)为独立信号源;当0<|ρik|<1时,称si(t)与s k(t)为相关信号源;当|ρik|=1时,称si(t)与s k(t)为相干信号源[13]。
对于独立或弱相关信号源,信号子空间的维数等于信源数K;而对于强相关或相干信号源,信号子空间的维数小于K,也就是说,相干信号源会导致协方差矩阵R秩亏缺,从而使子空间Us与Un估计错误。因此,传统的子空间类算法难以有效估计相干源DOA。
2 基于虚拟阵列变换和空间平滑的MUSIC 算法
本节简要介绍已有的相干源DOA 估计方法。对于具有移不变性的阵列结构,常用的相干源DOA估计方法是J.E.Evans 等人提出的空间平滑算法[7];对于一般的非移不变的阵列结构,考虑采用虚拟内插变换法将其变换为具有移不变性的虚拟阵列[11],再进行空间平滑。
空间平滑算法是将阵列分成若干个相同结构的子阵,对每个子阵的协方差矩阵进行平均运算,这样得到的平滑后的协方差矩阵,其秩得以恢复,从而实现解相干。但是,此方法是以牺牲阵列孔径为代价的,且只适用于具有移不变性的阵列结构。
虚拟内插变换法最早由Friedlander.B 等人提出。假设源信号位于某个角度范围Θ内,将Θ区间离散化,即将Θ划分为r个离散角度的集合,Θ=[θ1,θ2…,θr],其中θ1、θr为角度范围的左、右边界,且r>M,则与Θ=[θ1,θ2…,θr]相对应的原阵列的阵列流型为:

通过对虚拟阵列进行传统的空间平滑处理,可实现解相干,然后可采用一般的空间谱估计方法进行测角,如MUSIC 算法。
值得注意的是,虚拟内插变换需要到达角的范围,即需要确定信源到达角的大致位置。这里考虑采用Capon 算法[14]确定虚拟内插变换的角度范围。Capon 算法的基本思想是在期望方向信号功率不变的情况下,最小化总功率,也就是最小化噪声及非信源方向干扰功率,该算法的空间谱表示为:

由于Capon 算法对相干性不敏感,但与子空间类算法相比,其性能较差,且分辨率受波束宽度限制,因此考虑采用Capon 算法对空间谱进行一次搜索,取每个谱峰值处的一个波束宽度范围,取它们的并集作为虚拟内插的范围。
综上,基于虚拟阵列变换和空间平滑的MUSIC 算法流程总结如下。
输入:信源数K,阵列流型A,接收信号样本X;
输出:各信源的DOA 估计。
①用Capon 算法进行一次搜索,确定虚拟内插范围;
② 根据式(11)、(12)将原阵列变换为虚拟均匀阵列;
③针对虚拟均匀阵列,用空间平滑法进行解相干处理;
④ 利用MUSIC 算法得到DOA 估计。
理论上,基于虚拟阵列变换的空间平滑MUSIC 算法可以进行相干源DOA 估计,但是,虚拟阵列变换中引入的变换误差会降低最后的DOA 估计性能,且内插范围越大,变换误差越大。另外,空间平滑算法导致的孔径损失也会降低DOA 估计的精度与分辨率。
3 本文算法
现有的基于空间谱DOA 估计方法,都是利用阵列接收到的数据来构造信号子空间和噪声子空间,然后将阵列的导向矢量投影到噪声子空间来获得空间谱,并通过对导向矢量的搜索得到DOA 估计。与现有的方法不同,本节将提出一种DOA 估计的新方法,即基于投影矩阵搜索的DOA 估计算法,其基本思想是利用阵列结构来构造信号子空间的投影矩阵,再根据信号子空间和噪声子空间的正交性,得到噪声子空间的投影矩阵,然后将阵列接收到的数据投影到噪声子空间来构造空间谱,从而通过投影矩阵的搜索得到空间谱和DOA 估计。
3.1 算法设计
3.1.1 噪声子空间的构造
设信源数为K,将K个信源的DOA 写成矢量形式θ=[θ1,…,θK],由于信号子空间与导向矢量张成的空间是同一个空间,因此,利用阵列流型A(θ)=[a(θ1),…,a(θK)],可以得到信号子空间的投影矩阵[15]:

由式(14)、(15)可以看出,本文算法的子空间是根据阵列流型构造的,与信号无关。
3.1.2 数据样本的降维处理
为了提高该算法的抗噪声能力,同时降低算法的复杂度,这里先对信号样本进行时域降维预处理。将信号样本X进行奇异值分解,得到:

其中,U为左奇异矩阵,V为右奇异矩阵,D为一M×N维的对角阵;取V的前K列,记为V′,取D的前K列和前K行,记为D′,即保留信号空间的功率、去除噪声空间的功率,则降维处理后的数据样本为:

通常,N远大于K,通过上述处理将M×N维信号样本X降维成M×K维的X′,减小了后续的投影运算的计算量。
3.1.3 数据样本的投影和空间谱
将处理过的信号样本X′投影到噪声子空间,得到

由于X′始终位于信号空间,当θ为真实的到达角时,PN(θ)对应的噪声子空间与真实的信号空间正交,此时PN(θ)与X′正交,Z=O;当θ不是真实到达角时,该正交性不成立,即PN(θ)与X′不正交,Z≠O。
3.1.4 基于空间谱搜索的DOA 估计
因此,在可能的到达角范围内,通过对投影矩阵PN(θ)的搜索获得空间谱,参考上节的算法一,可能的到达角范围也可利用Capon 算法得到,本文算法的空间谱表示为:

最后通过峰值搜索,得到DOA 估计。
3.1.5 算法流程
基于上述分析和讨论,本文提出算法的流程总结如下。
输入:信源数K,阵列流型A,接收信号样本X;
输出:各信源的DOA 估计。
①用Capon 算法进行一次搜索,确定可能的到达角范围;
② 在可能的到达角范围内,根据式(14)和(15)计算噪声子空间的投影矩阵;
③根据式(16)、(17)将接收信号进行降维处理;
④ 根据式(18)、(19)计算空间谱,寻找峰值点,得到DOA 估计。
与算法一相比,本文算法是由阵列流型导出噪声子空间,而不是由数据的协方差矩阵导出的噪声子空间,因此理论上本文算法与信号的相干性无关,故对于相干源DOA 估计问题,本文算法无需进行解相干处理,从而避免阵列孔径的损失。此外,由于本文算法在满足布阵要求的情况下对不同阵列均可适用,无需进行虚拟变换处理,从而避免引入内插误差。
3.2 复杂度分析
设信源数为K,阵元数为M,快拍数为N,首先考虑基于虚拟阵列变换和空间平滑的MUSIC 算法(算法一)的复杂度,估计协方差矩阵的计算量为M2N,设虚拟内插变换的范围为Θ=[θ1,θ2…,θr],虚拟阵列变换的计算量为3M3+2M2r;设空间平滑子阵列的阵元数为m,则空间平滑的计算量为2(m2M+M2m)(M-m+1);最后采用MUSIC 算法在Θ上进行一维搜索,计算量为2m2K+K3。因此算法一的总的计算量约为M2N+3M3+2M2r+2(m2M+M2m)(M-m+1) +(2m2K+K3)r,由于r≫M,N≫M,计算量近似为O(M2N)+O(2m2K+K3)r。
下面考虑本文算法(算法二)的复杂度,信号样本矩阵奇异值分解的复杂度为O(MN2),投影矩阵的计算量为2MK2+M2K+K3,投影计算的计算量为M2K,本文算法需进行K维搜索,因此,算法二的计算量约为O(MN2)+O(2MK2+2M2K+K3)rK。
通过上述分析可知,在空间谱搜索部分,算法一是进行一维搜索,而算法二需进行K维搜索,因此算法二的计算复杂度较高。
4 仿真实验及分析
本节通过仿真实验对现有算法(算法一)和本文算法(算法二)的性能进行分析和比较。
仿真实验的条件设置为:五阵元的非均匀线阵(M=5),阵元设置为0.25λ[0,1,3,6,8],算法一的虚拟阵列设置为0.5λ[0,1,2,3,4],λ为波长;源信号为窄带高斯随机信号,相干源的相关系数为1;实验中,信噪比SNR 定义为阵列接收信号的总功率与噪声总功率之比,即:

另外,DOA 估计精度由均方根误差RMSE 来衡量,不失一般性,设独立实验次数为n,信源数为K,真实DOA 为 (θ1,…,θK),第i次实验的DOA 估计为,RMSE 定义为:
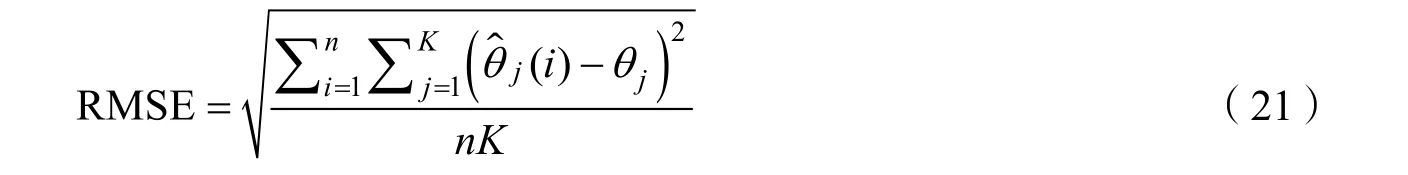
4.1 实验一:相干源的估计精度比较
参数设定:信源数K=2,DOA 为(70°,80 °),两信源相干;快拍数N=200;独立实验次数n=500;算法一的空间平滑子阵列的阵元个数取3。图1 为两种算法的RMSE 与SNR 的关系:图中蓝色曲线表示算法一的RMSE 随SNR 的变化关系;红色曲线表示算法二的RMSE 随SNR 的变化关系。
从图1 可以看出,对于相干源,算法二较算法一有更高的估计精度,在SNR 取值范围为2~12 dB左右时,算法一基本失效,而算法二仍可以有效估计DOA;在SNR 较高时,两种算法均可有效估计相干源DOA,但算法二的RMSE 较低,相差约0.5°~0.9°。

图1 两种算法RMSE 随SNR 变化曲线Fig.1 RMSE of two kinds of algorithm with various SNR
4.2 实验二:相干源的分辨率性能比较
参数设定:信源数K=2,DOA 为(70°,70°)ψ+,两信源相干;快拍数N=200;SNR=5 dB;独立实验次数n=500;算法一的空间平滑子阵列的阵元个数取3。图2 为两种算法的RMSE 与角度差ψ的关系:图中蓝色曲线表示算法一的RMSE 随角度差ψ的变化关系;红色曲线表示算法二的RMSE 与角度差ψ的变化关系。
从图2 可以看出,对于相干源,在不同的信噪比下,算法二较算法一都有更高的分辨率。在实验条件下,算法一在角度间隔大于14°左右时可有效进行DOA 估计(RMSE <2 °),算法二在角度间隔大于9°左右时可有效进行DOA 估计。
4.3 实验三:相干、非相关混合信源时的性能比较
参数设定:信源数K=3,DOA 为(70°,80°,100°),其中前两个信源相干,第三个信源与前两个信源不相关;快拍数N=200;独立实验次数n=500;算法一的空间平滑子阵列的阵元个数取4。图3 为两种算法的RMSE 与SNR 的关系:图中蓝色曲线表示算法一的RMSE 随SNR 的变化关系;红色曲线表示算法二的RMSE 随SNR的变化关系。
从图3 可以看出,对于相干、非相关混合源,算法二较算法一有更高的估计精度,在SNR 取值范围为5~12dB 左右时,算法一基本失效,而算法二仍可以有效估计DOA;在SNR 较高时,两种算法均可有效估计相干、非相关混合源DOA,但算法二的精度较高。
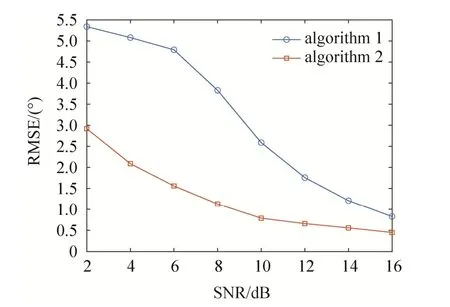
图3 相干、非相关混合源情况下,两种算法RMSE 随SNR 变化曲线Fig.3 RMSE of two kinds of algorithm with various SNR for coherent and non-correlation sources
5 结束语
本文提出的算法可以有效进行相干源DOA 估计,在已知信源数的情况下,无需进行解相干预处理,且适用于任意阵列。而传统的相干DOA 估计算法对于非均匀阵列,需要进行虚拟变换后再进行空间平滑,这样会引入变换误差,且空间平滑会损失阵列孔径。仿真结果表明,相较于基于虚拟内插变换的空间平滑MUSIC 算法,本文算法具有更优的精度与分辨率,这与理论分析一致。但是,传统DOA 估计算法的空间谱均为一维搜索,而本文算法的空间谱是K维搜索,因此本文算法的复杂度较高。后续工作将聚焦于如何降低本文算法的复杂度,可以考虑与其他算法如空域滤波[16]或STAP[17]相结合。

