基于加权相关的探地雷达后向投影成像算法*
陈鑫澎 李静霞 * 刘 丽徐 航王冰洁张建国
(1.太原理工大学新型传感器与智能控制教育部重点实验室,山西 晋中 030600;2.太原理工大学物理与光电工程学院,山西 晋中 030600)
地下管线在城市中扮演着能量输送、物质传输和信息传递的角色,被誉为城市的“生命线”[1-2]。然而,当今许多城市由于缺乏对地下管线的有效管理,造成对地下管线分布和埋设深度信息等的误判,导致在工程施工过程中事故频发,甚至造成爆炸等严重事故,因此地下管线的精准探测显得尤其重要[3-5]。在各种管线探测方法中,探地雷达因具有测量精度高、操作简单等优点被广泛应用。通常探地雷达使用一维或二维回波来完成目标识别,这种工作方式对操作人员的专业技能和先验知识提出了较高层次的要求,且目标检测存在处理速度慢、误判和漏判率高等问题。为了降低目标检测和识别的难度,探地雷达成像技术成为研究热点。其中,较为常用的成像算法有后向投影(back projection,BP)[6-8],逆时偏移(reverse time migration,RTM)[9-10],距离迁移(range migration,RM)[11-12],衍射层析(diffraction tomography,DT)[13-15]。利用DT 算法对探测目标进行反演时,反演过程过度依赖对探测环境的精准建模以及苛刻的近似条件,使其在实际使用中受到较大限制。采用传统的RTM 算法和RM 算法对分层介质进行探测时,目标的距离信息估计不准确,容易出现欠聚焦现象。而使用BP 算法对分层介质进行探测时,BP算法会对电磁波在不同介质表面发生的折射现象进行精确补偿,成像效果好,且该算法计算过程简单,易于工程应用,因此BP 算法在雷达成像技术领域得到了广泛应用。
经典的BP 算法通过计算各通道沿传播时延曲线的能量累加值,从而得到目标区域的能量聚焦。然而,这种“延时-求和”的方法会在成像结果中引入较强的伪影。在对目标进行探测时,该伪影易被误认为目标,从而造成误判。为了抑制伪影,国内外学者提出了不同的改进算法。Foo 和Zetik 等[16-17]提出了基于参考信号与回波信号互相关的BP 成像算法。该算法虽然在一定程度上抑制了伪影,但是对参考信号的选择有要求,因而增加了系统复杂度。周琳等[18-19]借鉴“延时-相乘-求和”的算法思想,提出了基于数据间互相关后向投影算法(cross-correlated back projection,CBP),该算法能抑制部分伪影,且无需引入额外参考信号。此外,张海如等[20]人提出了基于自相关的BP 算法来抑制伪影,但这种方法需要预先根据探测背景设定相关系数的判别阈值,不便于实际应用。
本文提出了一种基于加权相关的后向投影算法(correlation weighted back projection,CWBP)来抑制伪影。将该算法应用于频率步进探地雷达系统,用于对地下管线进行探测。进而,与经典BP 算法和CBP 算法相比较,分析了CWBP 算法的伪影抑制能力。
1 频率步进探地雷达测量原理
频率步进探地雷达采用频率步进信号作为探测信号,该信号是一种大时宽带宽积信号,基于此信号的探地雷达能同时兼顾分辨率和探测距离两方面的要求,因此在探地雷达领域中得到广泛运用[21-22]。
频率步进雷达的发射信号表示为:
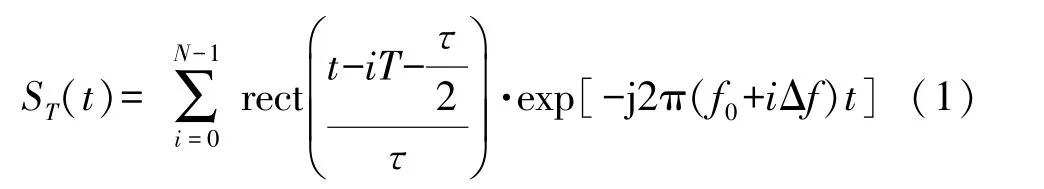
式中:T为脉冲重复周期,τ为脉冲宽度,f0为初始频率,Δf为频率步进量,N为频率步进数。
本振信号表示为:
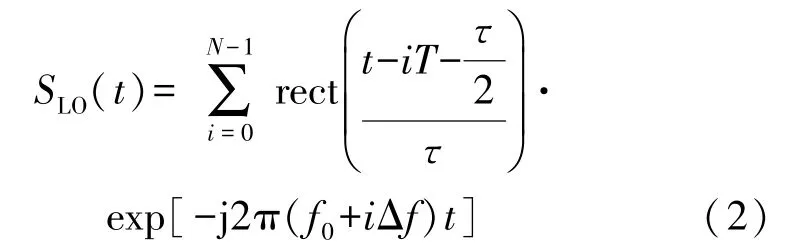
若目标管线与天线的径向距离为R,则回波信号可表示为:
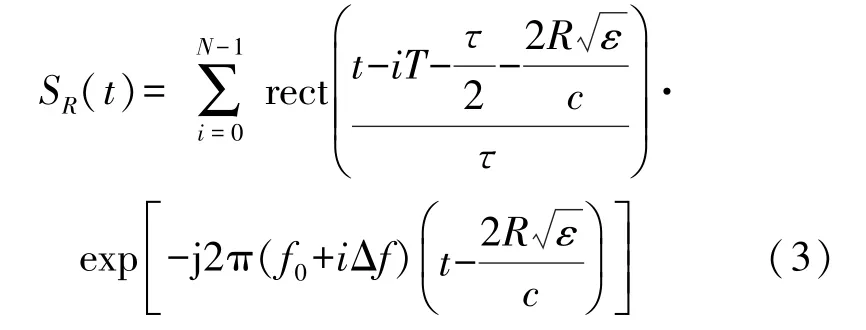
式中:c为光速,ε为介质的介电常数。
回波信号与本振信号进行混频后,其输出信号为:
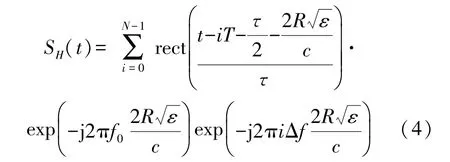
对式(4)进行归一化,之后对归一化后的方程进行逆傅里叶变换并求模可得到:
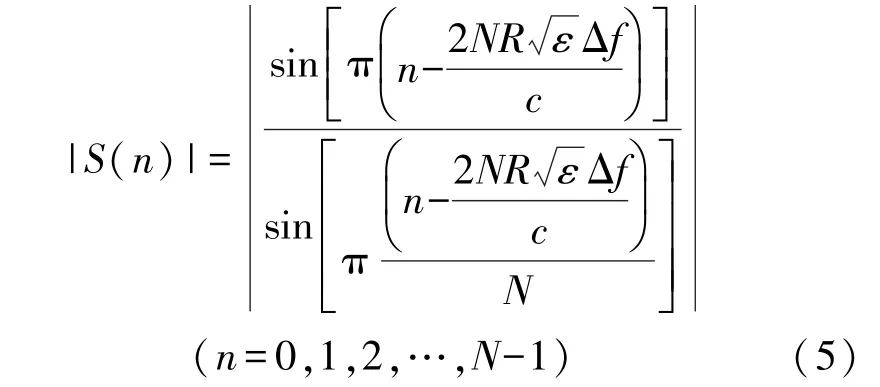
式中:S(n)为逆傅里叶变换后的信号。
根据式(5)可以得到目标的回波时延,进一步可将其转化为目标的一维距离信息。
2 加权相关后向投影算法
然后,采用CWBP 成像算法实现探测区域的二维成像。
经典BP 成像算法应用于探地雷达时,若合成孔径位置数目为M,对于任一成像点A,其到第i个合成孔径位置的时延τA,i,则得到A点到第i个孔径位置处的回波响应:
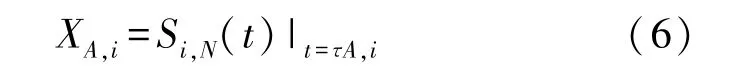
式中:N为采用点个数;Si,N(t)为预处理后第i个孔径位置处的A-scan 数据。
通过式(7)进行叠加,得到A点的成像结果:
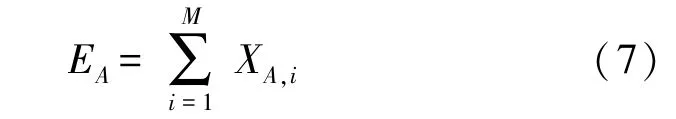
经典BP 算法会在成像结果中引入较强的伪影。为了抑制伪影,我们提出CWBP 成像算法。与经典BP 算法不同的是,任一成像点A 的回波响应在进行累加前,首先通过加权和相关处理进行重构。其目的是:通过加权处理,增强目标区域的反射能量;之后通过相关处理,削弱了非目标区域反射能量。因此,采用CWBP 算法,成像结果中的伪影得到了极大抑制。CWBP 成像算法具体的步骤为:
(1)对于任一成像点A,计算第i个合成孔径位置的时延τA,i,进而得到A点到第i个孔径位置处的回波响应XA,i。
(2)对成像点A到第i个合成孔径位置的回波响应XA,i进行加权处理。这里需要两组长度相等的数据Si,n(t)和SM/2,n(t)。其中,Si,n(t)为Si,N(t)中以t=τA,i为中心的一组数据;SM/2,n(t)为Si,N(t)中以t=τA,M/2为中心的一组数据。根据Si,n(t)和SM/2,n(t)得到皮尔逊加权系数:
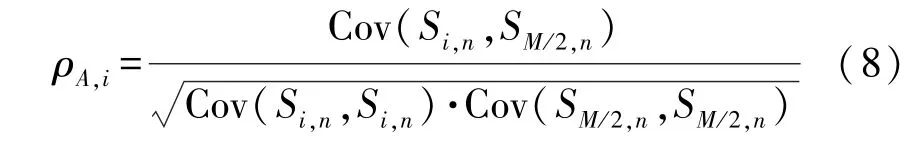
式中:Cov 函数表示两个向量的协方差。
利用该加权系数,对A点到第i个孔径位置的回波响应进行加权,得到加权后的回波响应:
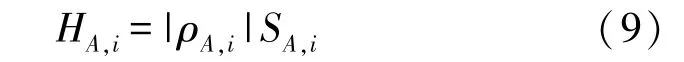
重复上述步骤,得到A点到各个合成孔径位置加权的回波响应:{HA,1,HA,2,…,HA,M}。
(3)对A点到各个合成孔径位置加权的回波响应进行相关处理。具体地,将A点到各个合成孔径位置加权的回波响应两两相乘,如表1 所示,然后取上三角部分,再按照式(10),将各列相加求和,重新构造得到A点到各个合成孔径位置的一次相关回波响应:。一次相关后,虚假目标和杂波干扰得到一定程度的消除。
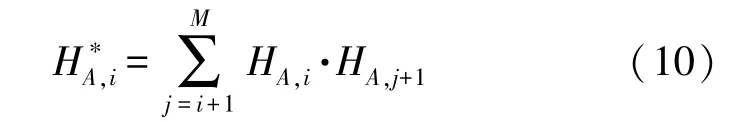
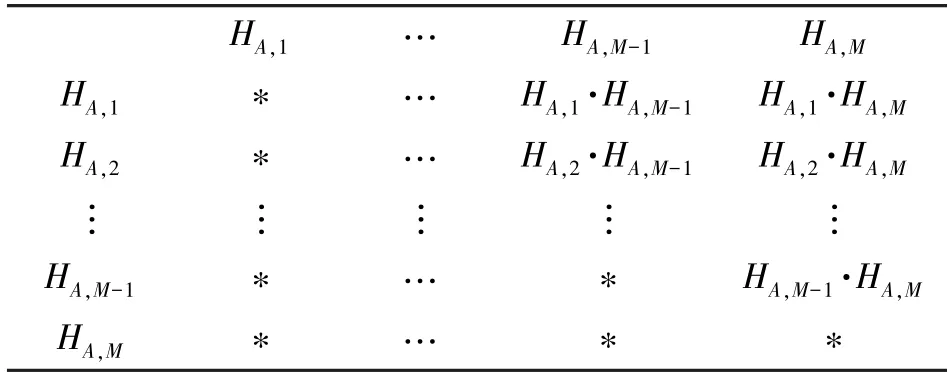
表1 相乘矩阵示意图
为了进一步消除杂波干扰,将一次相关的回波响应再次两两相乘,如表2 所示,然后取上三角部分,再按照式(11)将各列相加求和,最终构造得到A点到各个合成孔径位置的二次相关回波响应:。
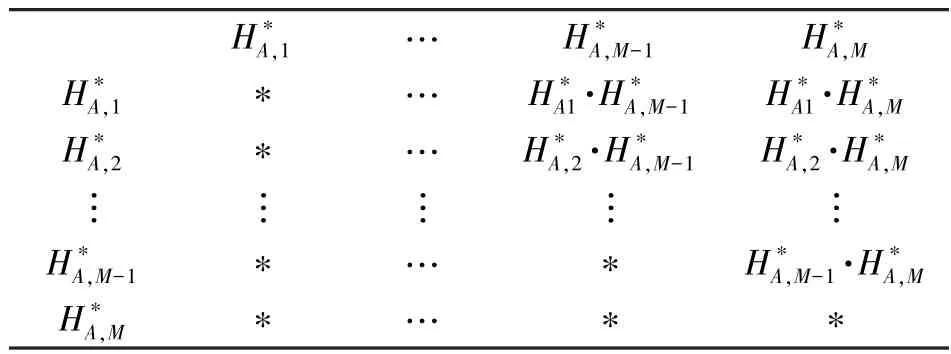
表2 相乘矩阵示意图
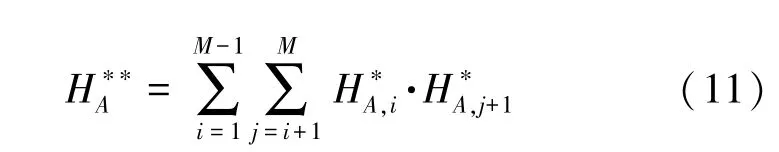
通过上述两步,得到A点的成像结果。通过遍历所有成像点,完成整个成像过程。
3 管线探测实验结果
3.1 实验装置
管线探测的实验装置如图1 所示,将管线埋设于规格为2.0 m×1.5 m×1.5 m 的沙池内,池内装有干燥河沙,干沙的相对介电常数约为3.3。实验中采用矢量网络分析仪(Rohde & Schwarz ZNB40)作为频率步进探地雷达,其产生的步进频率连续波的起始频率为1.8 GHz,终止频率为5 GHz,中心频率为3.4 GHz。收/发天线间距2 cm 并沿同一测线以相同的方向同时移动,每移动5 cm 进行一次测量,每个探测位置采集401 个频率点数据。

图1 实验场景图
3.2 单目标探测结果
首先对单根金属或PVC 管线进行了探测,分析了本文所提出的CWBP 成像算法的伪影抑制效果。实验中,PVC 管线的直径为0.20 m,长度为0.52 m,管壁厚度为3 mm,埋深度为0.60 m;金属管线的直径为0.10 m,长度为0.60 m,管壁厚度为2 mm,埋深度为0.32 m。管线探测的实验结果如图2 所示。对于PVC 管线,直接对回波信号进行经典BP 成像算法处理,从图2(a)中可以看到,成像结果中存在严重的直达波干扰。为此,在成像前首先对回波信号进行均值滤波,从图2(b)中看到地面直达波得到了有效的抑制。然而,经典BP 成像算法因采用“延时-求和”的方法实现对目标的定位,其成像结果中存在很强的伪影,严重影响了目标的识别。为了消除伪影,我们首先采用文献[18]提出的CBP 成像算法来代替经典BP 算法,可以看到:成像结果(图2(c))中的伪影得到了部分的抑制,残留伪影的存在仍然会影响目标的识别。为此,采用本文所提出的CWBP 成像算法,从成像结果(图2(d))观察到伪影几乎被消除。CWBP成像算法的伪影抑制效果显著优于经典BP 成像算法和CBP 成像算法。
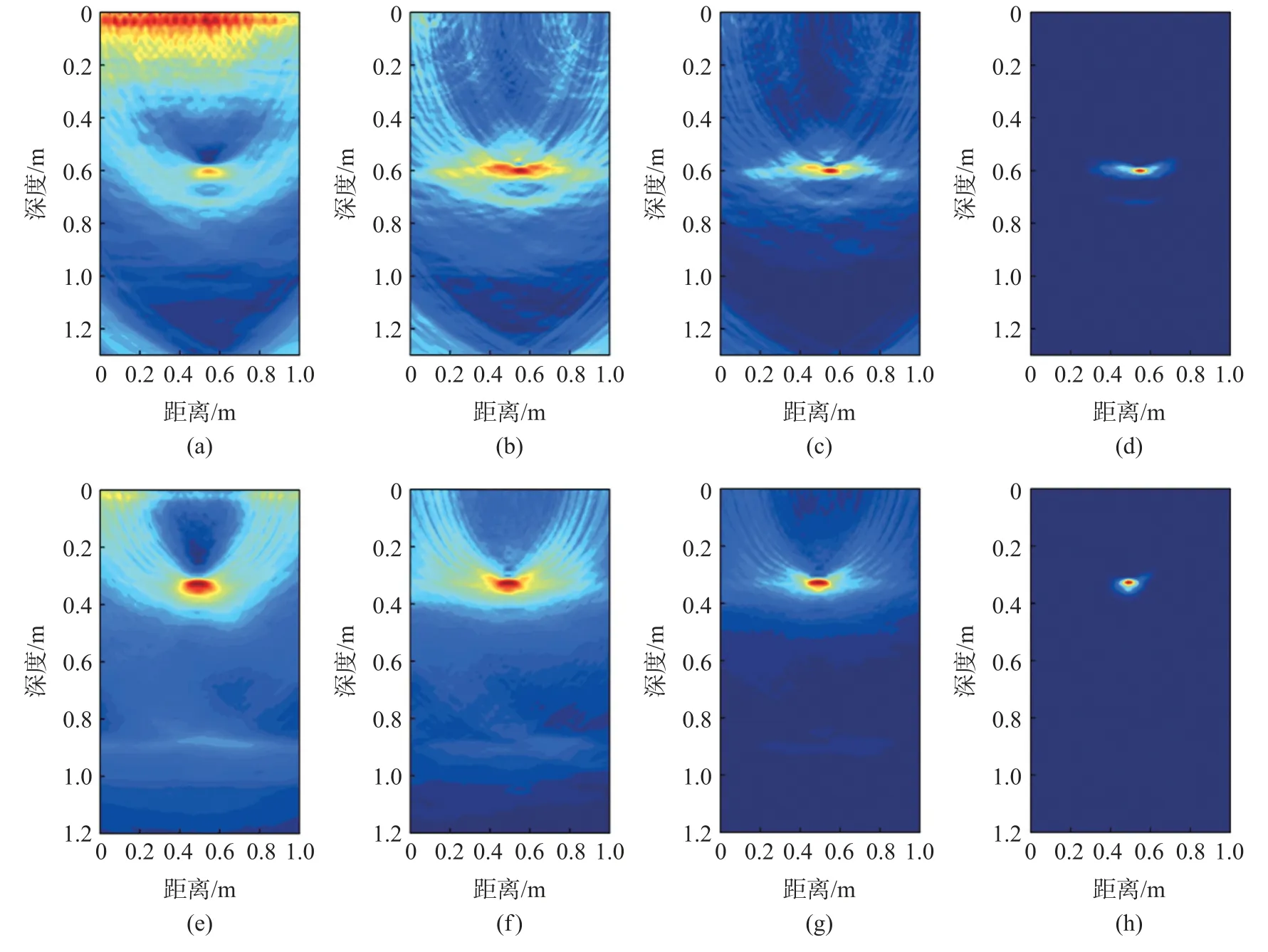
图2 PVC 管线和金属管线成像结果
对于金属管线的探测结果如图2(e)~(h)所示,结果与PVC 管线的探测结果类似。通过使用均值滤波有效地去除了地表直达波。此外,对比经典的BP 算法、CBP 算法、CWBP 算法的成像结果,可以看出CWBP 成像算法能显著抑制伪影,有利于对目标的识别。
此外,从分辨率的角度,分别给出了三种算法成像结果中峰值点位置在水平方向的剖面图。从图3和图4 中看到:不论是探测金属管线还是PVC 管线,CWBP 成像算法获得的剖面图中,峰值的主瓣宽度均有明显的缩减。该结果证明了CWBP 算法相较于经典BP 算法和CBP 算法,目标周围旁瓣干扰和背景杂波得到很好的抑制,目标的聚焦能力得到增强,进而提高了成像分辨率。
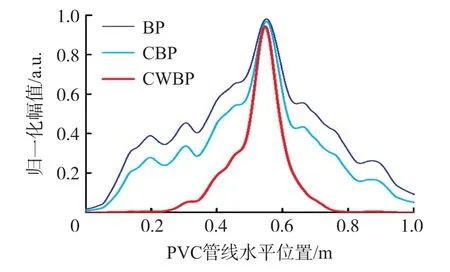
图3 PVC 管线峰值处水平剖面图比较
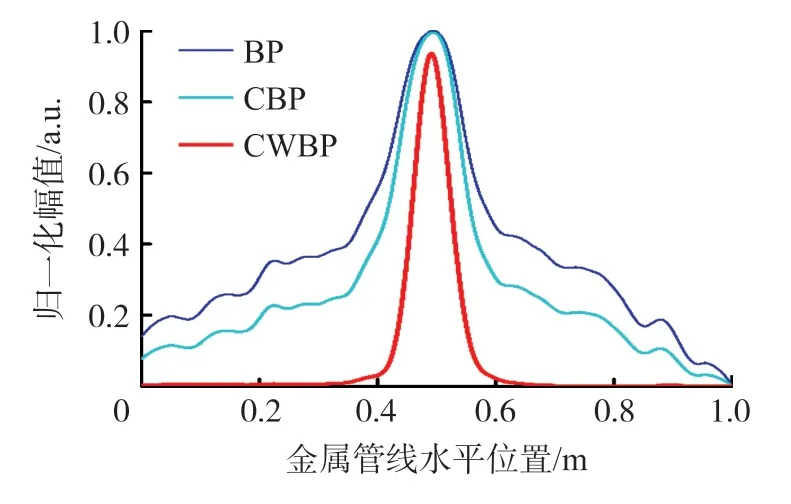
图4 金属管线峰值处水平剖面图比较
进而采用积分旁瓣比(integrated side lobe ratio,ISLR)、峰值旁瓣比(peak side lobe ratio,PSLR)、目标杂波比(target clutter ratio,TCR)定量分析了三种成像算法对杂波抑制的能力。
ISRL 定义为[23]:
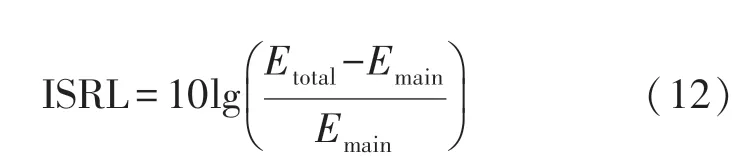
式中:Etotal和Emain分别表示图像的总能量和目标的主瓣能量。
PSLR 定义为[24]:
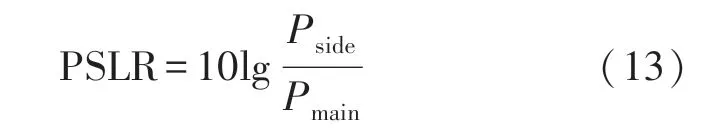
式中:Pside和Pmain分别表示旁瓣峰值能量和主瓣峰值能量。
TCR 数学表达式为[25]:
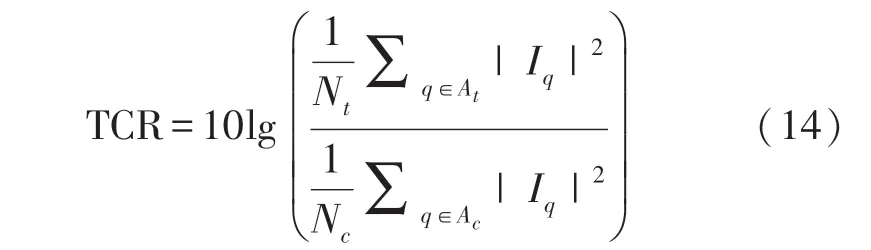
式中:Iq为图像中像素点幅值,Nt和Nc分别为目标区域At和杂波区域Ac的像素点数目。
表3 给出了上述三种成像算法的定量比较结果,其中ISLR值和PSLR值越小,说明旁瓣能量和旁瓣峰值相对目标主瓣能量和目标峰值越小,图像成像效果越好。TCR值越大,说明图像中包含杂波干扰越少,图像成像效果越好。从表3 中可以看出,无论探测管线类型如何,CWBP算法的上述三个指标值均远优于经典BP算法和CBP算法。定量分析结果证明CWBP算法具有优秀的伪影抑制效果。
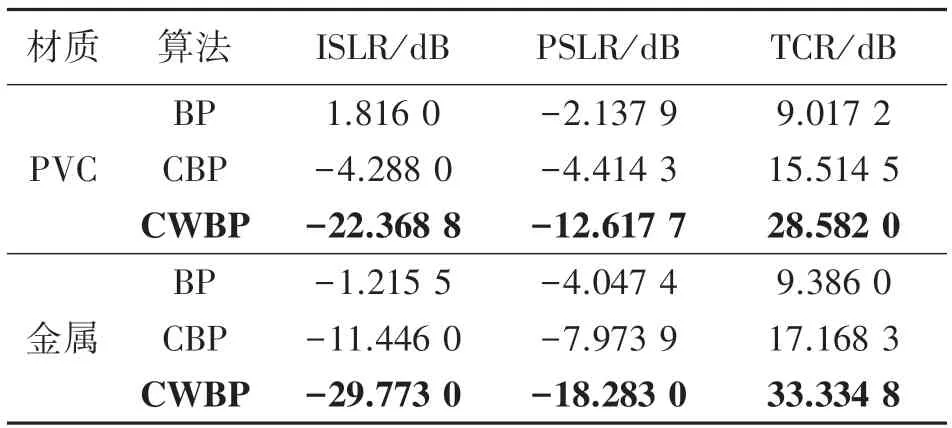
表3 成像算法衡量指标
3.3 双目标探测结果
在实际工程应用中,地下通常埋设有多根不同材质的管线。因此,本文将金属管线和PVC 管线同时埋设于干沙中进行探测,其示意图如图5 所示。其中,金属管线直径为0.13 m,长度为0.60 m,厚度2 mm,埋深0.38 m,水平位置距离0.38 m。塑料管线直径0.20 m,长0.60 m,厚度4 mm,埋深0.24 m,水平位置1.28 m,两者水平相距为0.90 m。
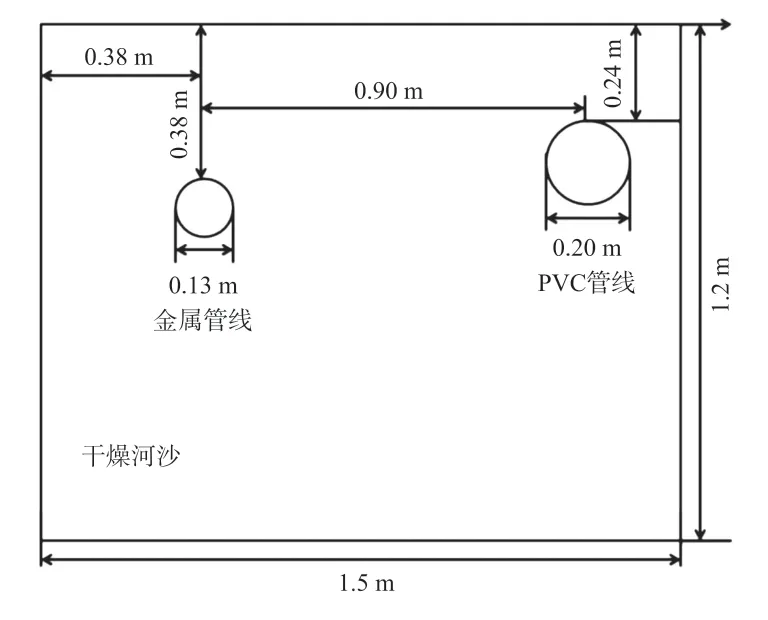
图5 金属和PVC 管线埋设示意图
成像的结果如图6 所示。未经预处理的经典BP 成像结果中,存在严重的直达波干扰(图6(a))。对数据进行均值滤波后,从6(b)中可以看出,直达波被有效抑制。然而,目标周围还存在较多的伪影。且两目标中间因伪影产生了叠影,造成了虚假目标。采用了CBP 算法,其成像结果(6(c))相较于经典BP 成像结果,伪影得到了部分的抑制。残留伪影以及叠影仍然会对目标识别造成干扰。采用CWBP算法,从图6(d)中可以看到,伪影及叠影得到了显著抑制,更加利于目标的识别。
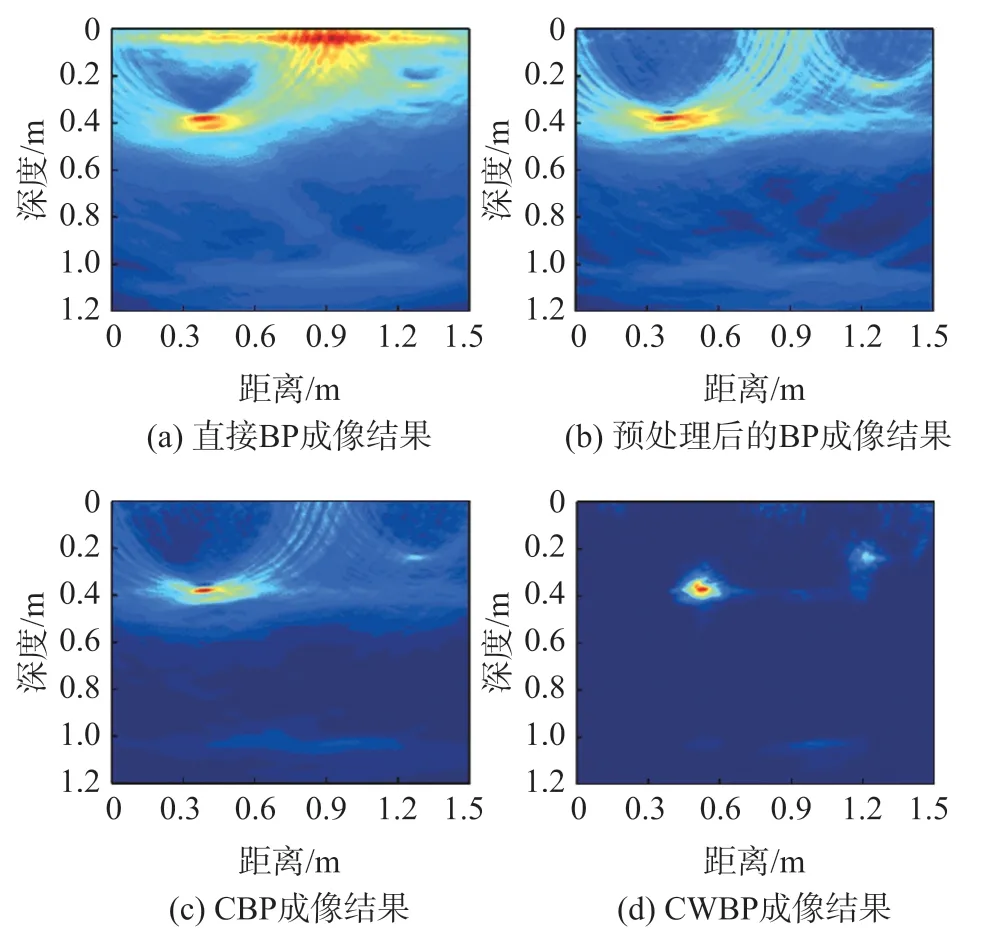
图6 双目标成像结果图
4 结论
本文提出了一种CWBP 成像算法,从实验数据得到的成像结果来看,该算法能显著抑制伪影。此外,对于双目标探测,该算法还能抑制双目标伪影产生的叠影。进而,分别采用了ISLR,PSLR,TCR 对结果进行量化分析,结果进一步证明CWBP 算法在目标成像方面,其伪影抑制能力均显著优于经典BP算法和CBP 算法。

