一种基于正交向量的极化相关衰减效应消除方法
罗章凯 裴忠民 熊伟 王新敏
(航天工程大学 复杂电子系统仿真实验室,北京 101416)
引 言
近年来,无线通信技术飞速发展,给人们的生活带来诸多便利的同时,通信频谱资源也愈发紧张. 当前,多输入多输出(multi-input multi-output, MIMO)技术迅速发展有效缓解了频谱资源紧张的问题,通过采用多天线收发的方式,大大提高无线通信信息传输效率[1]. 与此同时,双极化天线的应用,进一步从极化角度出发,开辟出新的维度用于信息传输. 如文献[2]利用多种极化天线发射信号,通过控制发射天线的极化方式实现极化复用,每次发送符号可以额外增加1 个比特. 正交极化天线承载信号间的幅度比和相位差承载信息,称为极化状态调制(polarization state modulation, PM)[3]. 这样的调制技术可以在射频进行调制,使放大器工作在线性区域,提高能效率[4-7];同时,PM 技术可以和传统幅相、频率调制技术结合,实现更高效的调制技术[6]. 文献[8]将极化状态看作信号的固有属性,将信息分为多个不同极化状态的极化信号承载,且线性叠加传输,接收端利用极化状态构建滤波矩阵,将多个极化信号分开后单独解调,实现基于极化滤波的高效传输. 文献[9]利用正交双极化构建四维调制星座图,每个符号可以承载更多信息,提高传输效率. 文献[10-14]利用信号极化状态研究物理层安全传输技术,开发极化信号处理技术在信息安全方面的潜能. 综上所述,极化信号处理技术在当前无线通信中具有巨大的潜力,也是当前研究的热点.
然而,双极化无线通信的传输介质并不是理想真空传输,复杂的电磁环境会造成发送信号的极化状态改变;同时,当前正交极化天线工艺难以做到正交极化间百分百隔离,以上两方面原因均会导致正交极化信号之间存在相互干扰,造成极化相关衰减(polarization-dependent loss, PDL)效应,恶化接收信号误码率性能.
当前针对PDL 效应的研究主要包括预补偿方法和迫零矩阵法[11,15-16]:预补偿方法在发送端对信道进行估计,利用估计的信道矩阵对发送信号进行处理,消除信道影响,从而消除PDL 效应,然而该方法中预补偿矩阵处理后的信号功率有一定损失;迫零矩阵方法在接收端对信道进行估计,并利用估计的信道参数对接收信号进行处理,从而消除PDL 效应,然而该方法中迫零矩阵处理后的噪声功率会增大,影响信号解调质量. 以上常用的两种方法虽在一定程度上能缓解PDL 效应,然而并不能完全消除.
针对PDL 造成的信号解调性能恶化问题,本文以PM 技术为研究对象,提出基于正交向量(orthogonal vector based,OVB)的PDL 效应消除方法. 该方法首先构建一组正交向量,假设为M个,并分为列向量互不相同的两组,每组M/2个,分别分配给水平(H)极化信号和垂直极化(V)信号. 然后,对H(V)极化信号,将发送信号分为多个部分,每个部分均乘以一个互不相同的正交向量后叠加发送,在接收端通过相同的正交向量处理接收信号,分离出信号的每个部分,从而恢复出发送信号. 再在发射端估计H(V)极化到接收端H(V)极化信道参数,并对发送信号进行处理,进一步消除信道影响,从而消除PDL 效应的影响,且不会放大噪声功率. 最后通过仿真验证本文所提方法相比于预补偿方法和迫零矩阵法实现更简单,误码率性能可以达到高斯信道下的理论值.
1 系统模型
系统模型如图1 所示,发送端(base station)和接收用户(user)均配备双极化天线,可以同时发送或接收H 极化和V 极化信号. 如果发送端直接发送极化信号,当前天线工艺和复杂的电磁传输环境将导致H 极化信号在V 接收天线处有响应,V 极化信号在H 接收天线处有响应,造成极化串扰,即PDL 效应.针对这个问题,本文提出OVB 的PDL 效应消除方法,旨在消除正交极化串扰. 本文方法亦可以推广到多用户多天线场景.

图1 系统模型Fig. 1 System model
1.1 信道模型
本文传输信道建模为莱斯信道[17],包含视距(line-of-sight,LoS)和非视距(non-line-of-sight,NLoS)分量,是无线通信中应用较为普遍的一种信道模型,可以表示为


NLoS 信道XPD 主要与环境导致的交叉极化耦合(cross-polar coupling,XPC)和接收端天线XPD 有关,可以表示为

1.2 信号模型及PDL 效应



图2 PM 星座点变换示意图Fig. 2 Transformation of PM constellation point

会引起极化状态在庞卡莱球面上刚性旋转,但不改变信号功率,星座点之间距离也不会变小. 然而,特征值不相等会造成调制星座点之间距离变小,造成误码率的恶化,这样的效应称为PDL.
显然,PDL 效应是由极化信道不均衡引起的,其程度与 λ1和 λ2的相异程度相关. 为了消除PDL 效应,需根本上解决特征值相异问题.
2 现有PDL 效应消除方法
当前PDL 效应消除方法主要有预补偿方法和迫零矩阵法[11].
(1)预补偿方法
预补偿方法在发送端通过对信道进行估计,利用估计的信道参数构建预处理矩阵对发送信号进行处理. 假设发送端可以获得准确的信道信息,根据式(9),预补偿矩阵可以表示为

式中,上标*表示矩阵共轭. 那么,接收信号可以表示为

综上所述,两种方法均能有效消除PDL 效应,然而会引起接收端信噪比下降的问题.
3 基于正交向量的的PDL 效应消除方法


图3 发射端信号处理流程Fig. 3 Signal processing at transmitter side

显然,此时接收的信号与理想信道下接收到的信号相同. 此外,经过正交向量处理后的噪声功率为


图4 接收端信号处理流程Fig. 4 Signal processing at receiver side
恢复H 和V 极化信号后,基于式(8)恢复出极化参数并解调出极化状态携带的信息,再将极化状态映射到庞卡莱球面,并与规则调制星座上的点比较,选择球面距离最小的点为判决输出点,即


图5 极化状态解调Fig. 5 Polarization state demodulation
PM 的误码率理论推导过程在文献[11, 19]中有详细描述,由于计算方法是标准方法,在此限于篇幅,不再重复叙述.
4 仿真分析
仿真中采用PM 星座图如图6 所示,分别为2、4、8、16 阶,星座点的相关参数可参照文献[19].
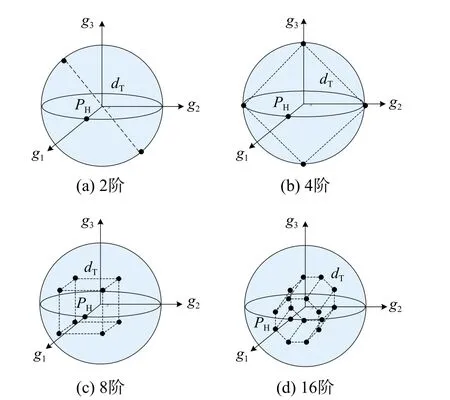
图6 PM 星座图Fig. 6 PM constellation
仿真中分别随机产生105个4 阶、8 阶和16 阶PM 符号(记为4PM、8PM、16PM),信道更新时间为200 个 符 号 时 间, 设 XPDant=15 dB, XPCenv=15 dB、K=10 、 ρt=1、 ρr=0.2、 σ2H¯=-12.7 dB. 图7 给出了不同阶数PM 信号在理想高斯信道下(信道矩阵为单位矩阵,信号解调只受到高斯白噪声影响)的误符号率理论值曲线和OVB 的PDL 效应消除方法的误符号率仿真曲线. 可见在调制阶数为4 阶、8 阶和16 阶情况下,本文提出方法的误符号率性能均可以逼近高斯信道下的理论值. 这是因为本文方法能有效消除PDL 效应,且不会放大噪声功率,从而实现双极化信号无串扰传输.

图7 不同阶数情况下OVB 方法误符号率与PM 理论值比较Fig. 7 SER performance comparison of OVB and theoretical value with different PM orders
图8 给出了不同 ρr情况下OVB 方法的解调性能. 可见, ρr分 别取 0 .2,0.4,0.6,0.8情况下,误符号率性能相近. 虽然极化参数的变化会改变正交极化之间隔离程度,从而加剧正交极化信号之间的影响,但本文方法可以有效消除PDL 效应,所以极化参数的改变对本文方法的信号解调性能基本没有影响.

图8 解调参数 ρr对OVB 方法解调性能影响Fig. 8 Effect of different ρr on the demodulation performance of the OVB method
仿真中随机产生105个4 阶PM 符号(记为4PM),信道更新时间为200 个符号时间,设 XPDant=15 dB,XPCenv=15 dB、K=10 、 ρt=1、 ρr=0.2、 σ2H¯=-12.7 dB. 图9给出了不同方法消除PDL 效应效果对比曲线,包括对接收信号直接解调方法、预补偿方法、迫零矩阵法和本文提出的方法. 同时,以理想信道情况下的PM 信号误符号率理论值曲线作为参照. 可见,直接解调方法得到的误码率性能最差,说明如果消除PDL 效应,信号解调性能将受到较大影响. 预补偿方法和迫零矩阵法的误码率性能比直接解调方法的误码率性能要好,然而比理论值差,这两种方法均会造成一定程度的信噪比下降,且PDL 效应越强,信噪比下降越大,解调性能也越差. 本文提出方法误码率性能能够逼近理论值,这是因为本文方法可以有效消除PDL 效应,且利用信道参数对发送信号进行处理,如式(22)所示,消除信道不利影响;且经正交向量处理后的噪声功率不发生变化,发送信号的信噪比未改变. 相比于其他方法,本文提出的方法性能更为优越,仿真结果与理论推导结果一致.

图9 PDL 效应消除方法对比Fig. 9 PDL effect elimination performance comparison
5 结 论
PDL 效应是双极化无线通信不可避免的问题,本文提出的方法可以有效消除PDL 效应,为进一步研究双极化无线通信相关技术打下基础. 本文中通过将发送信号分为多个部分,分别与正交向量相乘,叠加后形成一个混合矩阵. 下一步研究将结合加权类分数阶傅里叶变换技术对混合矩阵的部分列向量处理,从信息安全角度设传输方案,在解决PDL 效应的基础上研究物理层安全传输技术.

