科技创新提高碳排放效率了吗？

孙景兵，薛倩

（新疆大学 经济与管理学院，新疆 乌鲁木齐 830046）

习近平总书记在2021 年的全国“两会”上强调，“十四五”期间，中国将推动经济社会发展全面绿色转型，建设美丽中国，协同推进经济高质量发展和生态环境高水平保护，实现单位国内生产总值能耗和二氧化碳排放分别降低13.5%、18%；并提出在2030 年前实现“碳达峰”目标、在2060 年前实现“碳中和”目标。这表明，中国将在经济高质量发展的过程中同时完成低碳绿色转型任务，这是绿色发展史上的一大壮举，也是中国区别发达国家实现低碳转型的突出特征。寻找一条兼顾不断扩张的能源需求的低碳转型之路，提高碳排放效率、实现“碳中和”“碳达峰”的目标，是中国亟待解决的重要问题。因此，测算碳排放效率、探究科技创新对碳排放效率的影响效应及作用机制具有重要的现实意义。

本文可能的边际贡献：已有的文献大多通过因素分解角度将“碳排放强度”分解为能源结构、经济结构、要素替代、效率变动、技术进步等部分，在分解的基础上，进而研究技术进步、能源结构等因素对碳排放的影响方向和程度[1-3]。本文将采用非径向非期望产出SBM模型对2005—2018 年中国30 个省份的碳排放效率进行测算，进而研究科技创新对碳排放效率的影响及作用机制。

1 文献综述

关于碳排放效率问题的研究文献主要可以分为两类。一类是测算碳排放效率，进而研究某一因素对碳排放效率的影响作用，另一类则通过因素分解的方法，将碳排放分解为技术进步、经济结构、能源强度、经济增长等因素的影响效应，进而比较不同因素对碳排放的影响程度。本文将采用第一种方法研究碳排放效率问题，这种方法的研究文献主要可以分为以下几类。

一是碳排放效率的测算方法。碳排放效率的测算主要分为狭义和广义两种方法。狭义测算结果可称为：传统、单一要素的碳排放效率，通常为二氧化碳排放量和某一要素的比例。Zhang 等[4]采用人均二氧化碳排放量来衡量碳排放效率。王鑫静等[5]通过单位GDP 的二氧化碳排放量的倒数来衡量一带一路沿线国家的碳排放效率。广义测算结果可称为全要素碳排放效率，通常为通过多种投入、产出测算出来的效率。张晶和王丽萍[6]、张伟等[7]采用超效率DEA 模型测算碳排放效率。李涛和傅强[8]则基于非意愿变量Ruggiero 三阶段模型对1998—2008 年中国29 个省份进行碳排放效率的测算。Choi等[9]、Lucio 等[10]、邵海琴和王兆锋[11]等则采用SBMDEA 模型测算碳排放效率。赵阳[12]采用EBM 模型分析了2014—2018 年中国30 个工业细分行业的碳排放效率。马大来等[13]通过至强有效前沿的最小距离法测算了1998—2011 年中国各省份的碳排放效率。孙海燕和耿成轩[14]通过随机前沿分析法测算中国区域的碳排放效率以及时空异质性。相较于狭义的测算方法，广义的测算方法更加科学，传统、单一要素的碳排放效率的测算方法忽略了实际生产过程中不同要素之间的替代性。

二是科技创新对碳排放效率的影响作用，主要包含两类：一是科技创新对碳排放效率起促进作用，二是科技创新对碳排放效率起抑制作用。促进作用的相关研究如：王群伟等[15]将二氧化碳排放绩效指数分解为技术效率、技术进步，其研究结果表明，技术进步的增长作用大于技术效率的退化作用，所以技术进步可以提高二氧化碳排放绩效。魏巍贤和杨芳[16]、李涛和傅强[8]认为技术进步会提高自然资源利用率，降低能源的消耗量，减少污染排放，提高碳排放效率。原毅军等[17]提出技术进步通过新产品与新技术、回弹效应影响能源利用效率，进而影响碳排放效率。杨莉莎等[3]定量分析了2005—2015 年中国不同产业、不同区域之间各驱动因素对二氧化碳减排效率的影响，其研究结果表明，技术进步通过促进效应、反弹效应（收入效应、替代效应、经济层面的反弹效应）影响碳排放效率，且技术进步对外部环境较敏感。邵海琴和王兆锋[11]探讨了长江经济带旅游业碳排放效率变化的影响因素，其研究结果表明，技术创新因素对碳排放效率的提升具有促进作用，但在不同省份存在较大差异。抑制作用的相关研究如Acemoglu等[18]认为技术进步在促进经济增长的同时，引发“反弹效应”，导致能源消耗量增加，从而碳排放量的增加。赵阳[12]采用EBM 模型分析了2014—2018 年中国30 个工业细分行业的碳排放效率及影响因素，研究表明技术创新的提高会对行业碳排放效率的提升产生阻碍作用。

综上所述，关于科技创新对碳排放效率的影响研究已经较为深入与全面，研究思路也非常丰富，为后续研究奠定了理论基础，但是上述研究存在一些缺陷：第一，局限于某一行业或某一地区，样本数据的局限会影响研究结果的准确性。第二，大多数研究仅通过因素分解的方法，研究技术进步、科技创新对“碳排放”的影响效应。第三，研究仅限于科技创新对碳排放效率的影响作用，未能进一步分析其作用机制。本文在已有的研究基础上采用非径向非期望产出SBM 模型，测算2005—2018 年中国30 个省份的碳排放效率，以实证研究为基础，分析科技创新对碳排放效率的影响，并探究其作用机制，以期为中国绿色低碳发展提供参考。

2 碳排放效率的测度

2.1 碳排放效率的测算方法

效率的测算方法主要有数据包络分析法（DEA），DEA 由于不用对投入、产出变量之间的函数进行假定，避免了人为主观因素的影响，被广泛应用于效率评价的研究之中。但是传统的DEA 模型认为在生产过程中高效率表现为投入少、产出高，忽略了生产过程中的“环境负外部性”问题。在经济生产过程中，既伴随着期望产出，如国内生产总值，又伴随着非期望产出，如二氧化碳、二氧化硫、烟（粉）尘等污染物的排放。所以绿色低碳发展的高效率应该表现为投入少、期望产出高、非期望产出少。Tone[19]构造了基于松弛变量的SBM 测度模型，将松弛变量直接纳入目标函数。Tone[20]认识到生产过程中存在大量污染物，将非期望产出加入SBM 模型，不仅解决了产出中存在非期望产出的问题，还克服了投入与产出变量的松弛问题，有效地测算了环境效率。因此，本文根据Tone 提出的非径向非期望产出SBM 模型测算了规模报酬可变情况下的碳排放效率。选取各个省份作为一个决策单元，每个决策单元均有投入、期望产出、非期望产出三种投入产出向量。考虑N种投入（x），M种期望产出（y），I种非期望产出（z），SBM 模型可表示为：

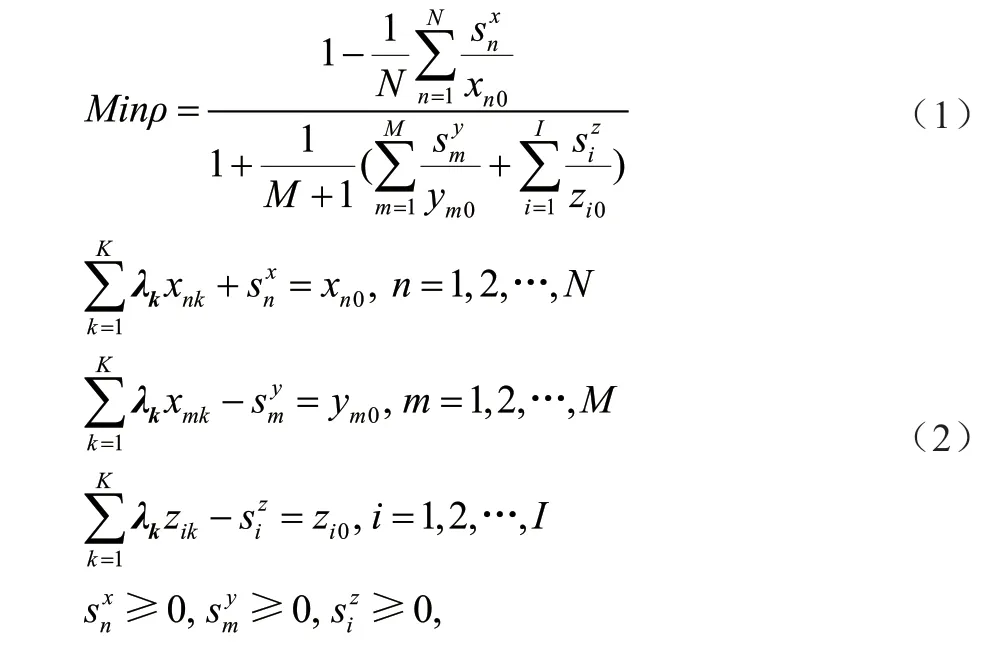
式中：ρ为需要测算的碳排放效率值，取值范围为[0, 1]；、 、 分别为投入、期望产出与非期望产出的松弛量；λ 为权重向量。

2.2 数据处理

本文选取2005—2018 年中国30 个省份（由于西藏和港澳台地区大量数据缺失，将其排除于样本之外）的投入、产出要素测算碳排放效率。以资本、劳动力、能源消耗量为投入要素，以各省份的实际国内生产总值为期望产出、二氧化碳排放量为非期望产出进行碳排放效率的测算。

2.2.1 投入要素

资本投入。目前学术界尚未形成统一的资本存量测算标准，本文参考了张军等[21]的研究成果，采用“永续盘存法”对每年的实际资本存量进行测算：本期物质资本存量=本期固定资产形成总额+上期物质资本存量×(1-9.6%)（各省份固定资本形成总额的固定资产折旧率是9.6%）。同时，本文将采用其计算得出的2000 年的资本存量作为初始值，并以2000 年为基期进行计算。

劳动力投入。劳动力指标的选取应该包括既包括劳动力数量又包括劳动力质量，但是由于“劳动力质量”数据较难获得，本文仅选取各省份的就业人数衡量劳动力投入。

能源投入。生产过程中投入的能源用各省份每年的能源消耗量来表示，由于各个省份的能源消费种类不一，将煤炭、电力等能源的消耗量按照其与标准煤的折算关系统一转换为标准煤，加总之后得到各省份历年的能源投入量。

2.2.2 产出要素

期望产出。以各省份的国内生产总值作为期望产出的指标，为了消除通货膨胀的影响，根据各省份的国内生产总值指数对名义国内生产总值进行平减（以2005 年为基期），得到各省份的实际国内生产总值。

非期望产出。以各省份的二氧化碳排放量作为非期望产出，数据来源于Wind 数据库。

2.3 测算结果

如图1 所示，碳排放效率较高的地区包括北京、天津、上海、黑龙江等，相对较低的地区包括宁夏、新疆、贵州、山西等。在2005—2018 年之间，除河南、广西、内蒙古、山西、新疆之外，中国其他地区碳排放效率均呈现上升趋势，但上升幅度各有不同。

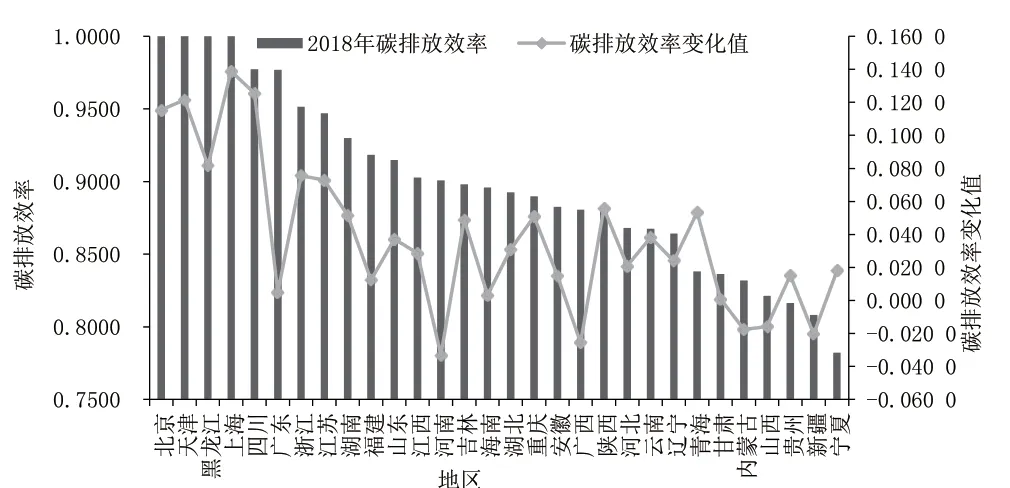
图1 2018年中国各地区的碳排放效率及2005—2018年碳排放效率变化值

这是因为中国近年来实施了一系列针对地区、行业、企业的节能政策，环境治理、绿色低碳发展卓见成效。如“十一五”时期，实施了《千家企业节能行动》（发改环资〔2006〕571 号）等政策。2007 年，批复了天津、河北、山西、内蒙古、江苏、浙江、河南、湖北、湖南、重庆、陕西11 个地区开展排污权交易制度试点。2009 年，中国首次量化温室气体减排目标“2020 年单位GDP 碳排放比2005 年降40%～50%”。《节能减排“十二五”规划》提出，坚持绿色低碳发展、加强用能节能管理、推动减排技术的创新、推广以及应用、开展碳排放交易试点工作等。2013—2014 年，中国在北京、天津、上海、重庆、深圳、广东、湖北7 个地区陆续开展碳交易试点工作。2017年，《全国碳排放交易市场建设方案（发电行业）》提出以电行业为突破口率先提出启动全国碳排放交易体系。随着一系列节能减排政策的制定与实施，二氧化碳的排放量逐渐减少，碳排放效率处于上升趋势。

由于中国碳排放效率在不同地区存在着巨大差异，效率最高值为1，最低值为0.736 6。本文将30 个省份按照经济发展水平划分为东、中、西三个区域①东部地区：北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南。中部地区：山西、内蒙古、吉林、黑龙江、安徽、江西、河南、湖北、湖南、广西。西部地区：重庆、四川、贵州、云南、陕西、甘肃、青海、宁夏、新疆。。如图2所示，在三个区域中，东部地区的碳排放效率水平最高，其碳排放效率的最小值为0.882 7，最大值为0.939 7。西部地区的碳排放效率水平较低，其碳排放效率的最高值为0.855 0，远小于东、中部地区（中部地区碳排放效率的最小值为0.877 6）。这是因为东部地区的经济发展水平、科技创新水平较高，产业结构较为合理，且排污权、碳排放交易等试点工作多在东部地区开展，在生产过程中能源利用效率较高，二氧化碳排放量较少，所以东部地区的碳排放效率水平优于相对落后的中、西部地区。

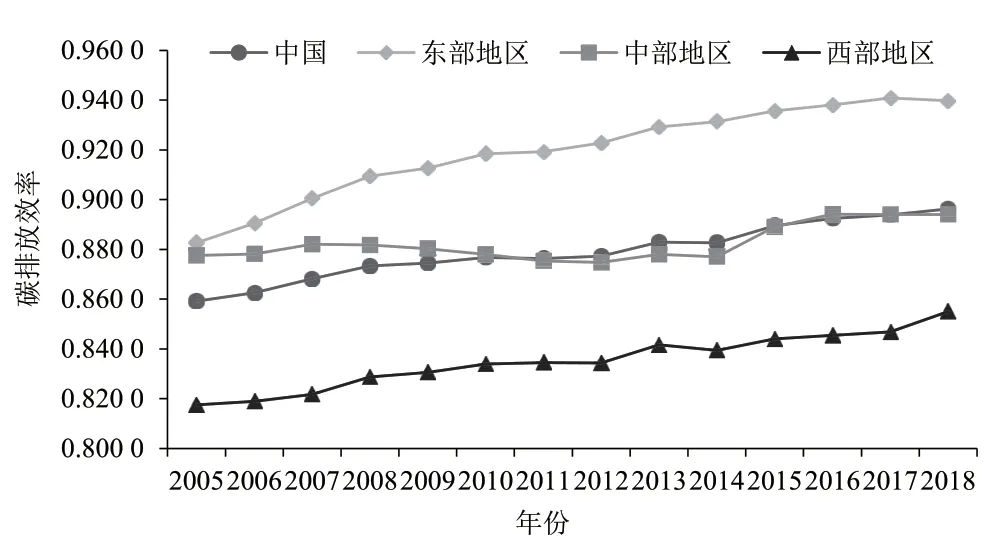
图2 2005—2018年中国整体及东、中、西三个区域的碳排放效率

3 计量模型、变量与数据

3.1 计量模型

由 于 设 定 形 式 简 洁，Harrison[22]、York 等[23]将IPAT 等式作为分析环境变化驱动因素的模型框架，但是IPAT 等式不允许各影响因素不同比例地变化，Dietz &Rosa[24]将IPAT 等式进行改进，以随机形式表示，建立STIRPAT（stochastic impacts by regression on population,affluence and technology）模型。本文以STIRPAT 模型为基础，构建了科技创新对碳排放效率影响的实证模型。STIRPAT 模型的基本形式为：

式中：I表示环境影响，P表示人口总量，A表示富裕度，T表示科技创新水平，表示随机误差项；为了尽量减小或消除异方差的影响，对式（3）进行对数处理，得到了式（4）：

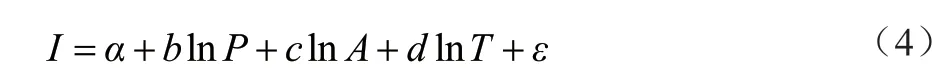
本文主要探究科技创新对碳排放效率的影响效应，所以选取碳排放效率为被解释变量，科技创新为主要解释变量，并在此基础上选择经济发展水平、人口规模为次要解释变量。为了控制其他因素对碳排放效率的影响，本文在估计方程中加入了其他的控制变量：城镇化水平、产业结构、对外开放程度、能源消耗量。最终构成的模型为：

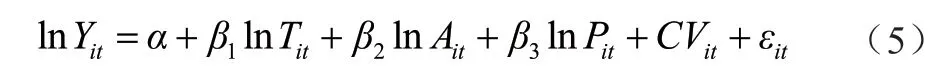
式中：Y表示碳排放效率，T表示科技创新水平，A表示经济发展水平，P表示人口规模，下标i、t分别表示省份、年份，α为个体异质性，ε为随机扰动项。

3.2 数据来源与处理

本文数据来自EPS 数据平台、中经网数据库、Wind 数据库。表1 分析了相关变量的均值、标准差、最小值、最大值等描述性统计特征。

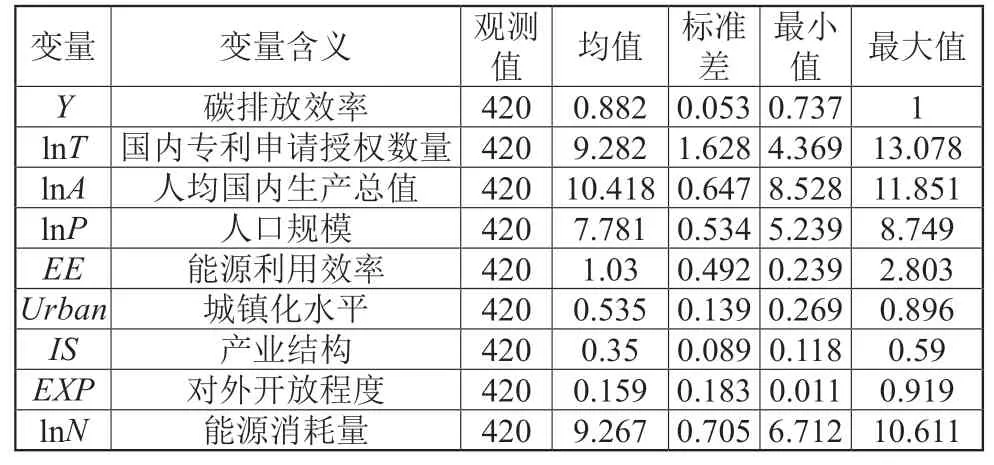
表1 主要变量的描述性统计

科技创新水平（T）：以国内专利申请授权数量来衡量该省份的科技创新水平。经济发展水平（A）：以人均国内生产总值来衡量各省份的经济发展水平，由于经济发展水平与碳排放效率之间可能存在二次关系，所以加入了人均国内生产总值的平方。人口规模（P）：人口规模用人口密度，即地区人口数量与行政区域面积的比例来衡量。城镇化水平（Urban）：城镇化水平用城镇人口数量占该区域总人口数量的比重来衡量。产业结构（IS）：产业结构用工业增加值占国内生产总值的比例来衡量。对外开放程度（EXP）：对外开放程度用出口额占国内生产总值的比例来衡量。出口额通过当年的12 个月的平均汇率换算成人民币，进行计算。能源消耗（E）：生产过程中投入的能源用各省份的能源消耗量来表示，由于各个省份的能源消费种类不一，本文将煤炭、电力等能源的消费量统一转换为标准煤。

4 实证分析

4.1 基准分析

为深入探究科技创新对碳排放效率的影响，本文根据式（5）进行OLS 回归，从整体上分析科技创新及其他影响因素对碳排放效率的作用效果，表2 给出了式（5）的基准回归结果。

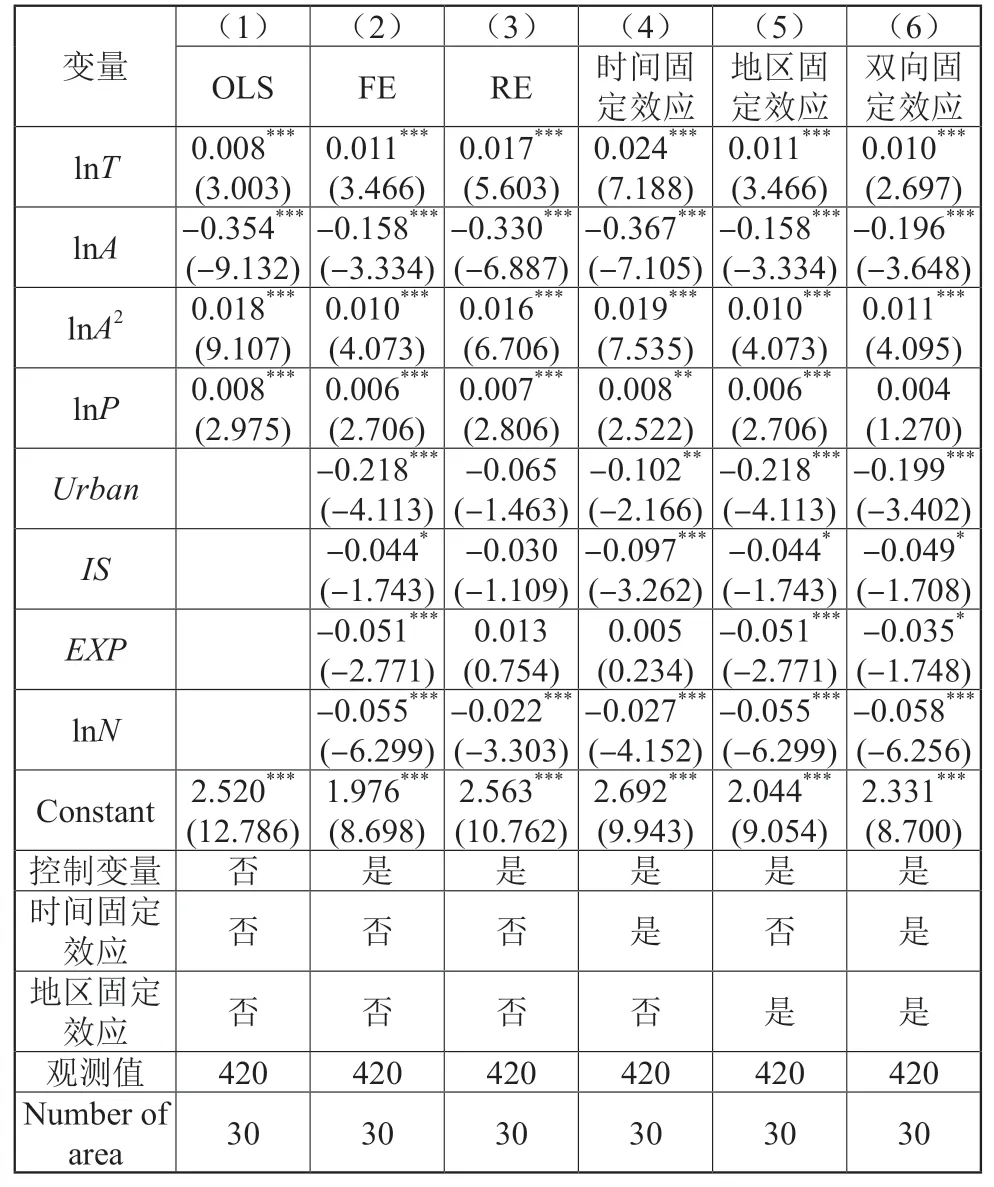
表2 基准回归结果

其中，第（1）列不加入任何控制变量、固定效应，用科技创新水平、经济发展水平、人口规模对碳排放效率直接进行回归，结果显示科技创新水平对碳排放效率有显著的正向促进作用。第（2）、第（3）列则加入了一系列控制变量的固定效应模型、随机效应模型（从Hausman 检验来看，P值为0.000 0，强烈拒绝原假设，即固定效应模型的效果优于随机效应模型）。第（4）、第（5）列分别在第（2）列的基础上进一步控制年份固定效应、地区固定效应，科技创新对碳排放效率仍保持显著的正向促进作用。第（6）列为最终的基准模型，在控制了诸多因素之后，估计结果仍然显示科技创新对碳排放效率有促进作用，且在1%的显著性水平上成立。控制变量的回归结果也符合预期效果。

实证结果表明：科技创新水平每增加1 个单位，碳排放效率增加0.01 个单位，且在1%的水平上通过显著性检验，即科技创新水平与碳排放效率呈现显著的正相关关系。科技创新水平的提高可以拓宽能源来源广度，提高废气处理水平，减少能源消耗量，从而减少二氧化碳排放量，提高碳排放效率。不同的产业部门对能源的需求不同，不同的能源利用效率也会产生不同的二氧化碳排放量，科技创新可以推动高能耗、高污染行业转型升级，优化不同产业不同部门之间的能源消费结构，发展低碳产业，从而提高碳排放效率。

经济发展水平对碳排放效率的影响：经济发展水平变量的一次项系数为负，二次项系数为正，二者均在1%的水平上通过显著性检验。说明经济发展与碳排放效率之间存在正“U”型关系，碳排放效率随着经济发展先降低，经过拐点后，经济发展会导致碳排放效率增长。人口规模与碳排放效率呈正相关关系：人口密度越大，使用能源的成本越小，碳排放效率越高。城镇化水平与碳排放效率呈显著地负相关关系：城镇化水平越高，带动了区域基础设施的建设，导致能源的消耗量急剧增加，降低了碳排放效率。产业结构与碳排放效率呈显著地负相关关系：工业产业在产业中的占比越高，则说明该地区处于工业化进程中，对化石能源的需求就越大，而且由于经济发展方式较为粗放，能源利用效率较低，在能源利用过程中排放了大量的二氧化碳，该区域的碳排放效率就越低。对外开放程度在整体样本中与碳排放效率呈负相关关系，可能是因为中国由于科技创新水平不高而处于国际贸易中的劣势地位，出口的多为隐含碳排放量较多的商品，所以碳排放量较低。能源消耗量与碳排放效率呈显著地负相关关系，能源消耗量越大，导致能源利用产生的二氧化碳的排放量越大，碳排放效率就越低。

4.2 机制分析

科技创新可以通过提高能源利用效率进而提高碳排放效率，但是不同地区表现出明显的区域差异，这就引发了对以下问题的思考：能源利用效率是否影响科技创新对碳排放效率的提升作用？科技创新对碳排放效率的影响效应是否随着能源利用效率而具有差异性？本文将对此进行考察。

借鉴Lyubich 等[25]做法，本文以能源生产率来衡量各省份的能源利用效率。能源利用效率（Energy efficiency）由国内生产总值与能源消耗量的比值来表示。中介效应的检验方法众多，在统计检验错误和检验功效方面各有优劣，Judd & Kenny[26]、Baron & Kenny[27]提出通过逐步法检验中介效应，即依次检验回归系数。Mackinnon 等[28]提出的单一方法的适用性较低，而且第一类错误率太大，远超过给定的显著性水平。温忠麟 等[29]在 结 合Judd & Kenny[26]、Sobel[30]、Baron &Kenny[27]等提出的不同检验方法的基础上，构造了一个综合的中介效应检验程序，能在较高统计功效的基础上控制第一类和第二类错误的概率。在模型构建方面，主要借鉴了钱雪松等[31]的做法，进一步选取能源利用效率作为中介变量进行中介效应检验，方程如式（6）～（8）所示。

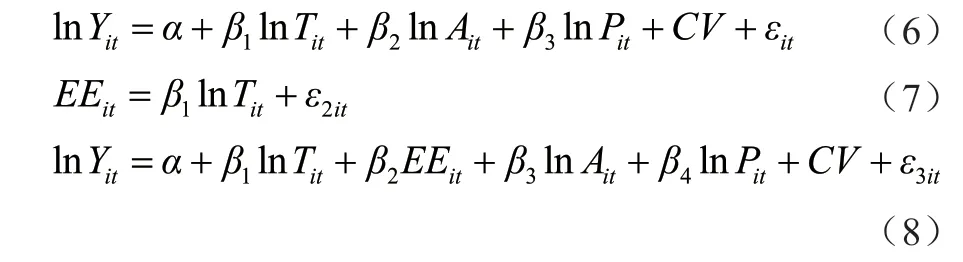
表3列出了影响机制验证的结果，可以发现在科技创新改变能源利用效率以影响碳排放效率过程中，Sobel检验中的Z 统计量为2.704，大于5%显著性水平上的临界值0.97，因而存在以能源利用效率为中介变量的中介效应，该中介效应在总效应中所占比例为43.85%。这些结果表明：在科技创新对碳排放效率施加影响的过程中，能源利用效率发挥了重要作用。具体而言，如果地区的科技创新水平提高，此时能源利用效率会因之而提高。在此基础上，能源利用效率提高会减少二氧化碳排放量，因此，碳排放效率也会随能源利用效率的提高而增加。

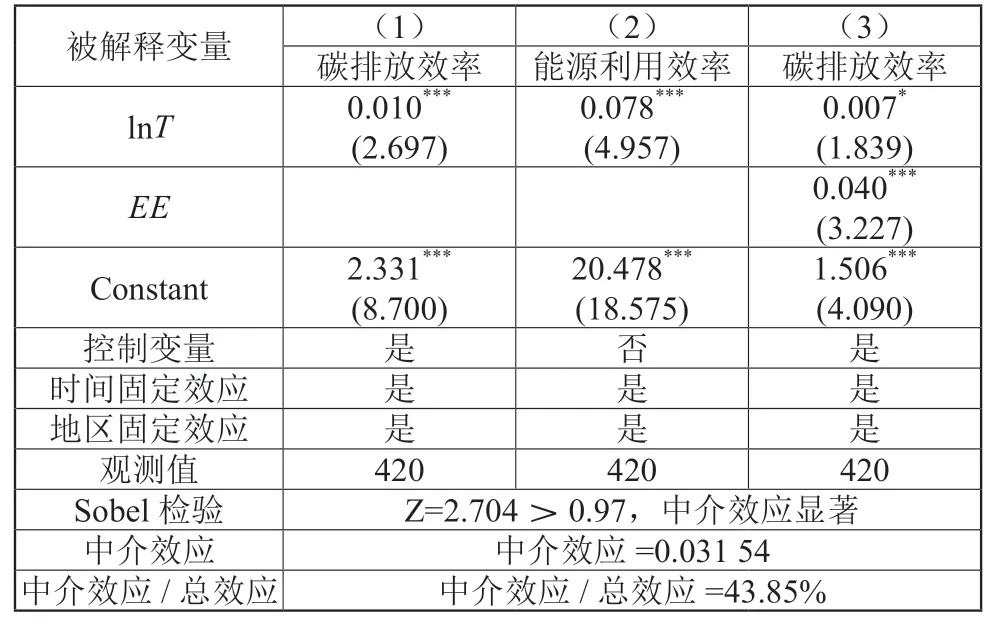
表3 科技创新通过能源利用效率影响碳排放效率的中介效应

基于中介效应的计量检验清晰地揭示出，中国存在“科技创新—能源利用效率—碳排放效率”环节。同时，以能源利用效率为中介变量的中介效应作用效果显著，说明能源利用效率发挥重要作用。

4.3 异质性分析

分地区回归分析。由于中国幅员辽阔，不同区域在经济发展水平、能源结构等诸多方均存在差异，导致碳排放效率存在较大差异，本文将中国的30 个省份按照经济发展水平划分为东、中、西三个区域，进一步探究不同区域之间科技创新对碳排放效率的差异，结果如表4 所示。第（1）、第（2）、第（3）分别是东、中、西三个区域科技创新对碳排放效率的回归结果。通过对比发现，西部的科技创新水平对碳排放效率的正向促进作用明显高于东部地区和中部地区，即经济发展水平越低，科技创新对碳排放效率的促进作用越高。这是因为西部地区的科技创新水平较为落后，在提高科技创新水平上还有很大空间，从而对碳排放效率的促进作用较明显；东部地区的科技创新水平走在中国前列，属于科技创新水平较为发达的区域，科技创新水平的提高空间较小，东部地区科技创新水平对碳排放效率的促进作用较微弱。

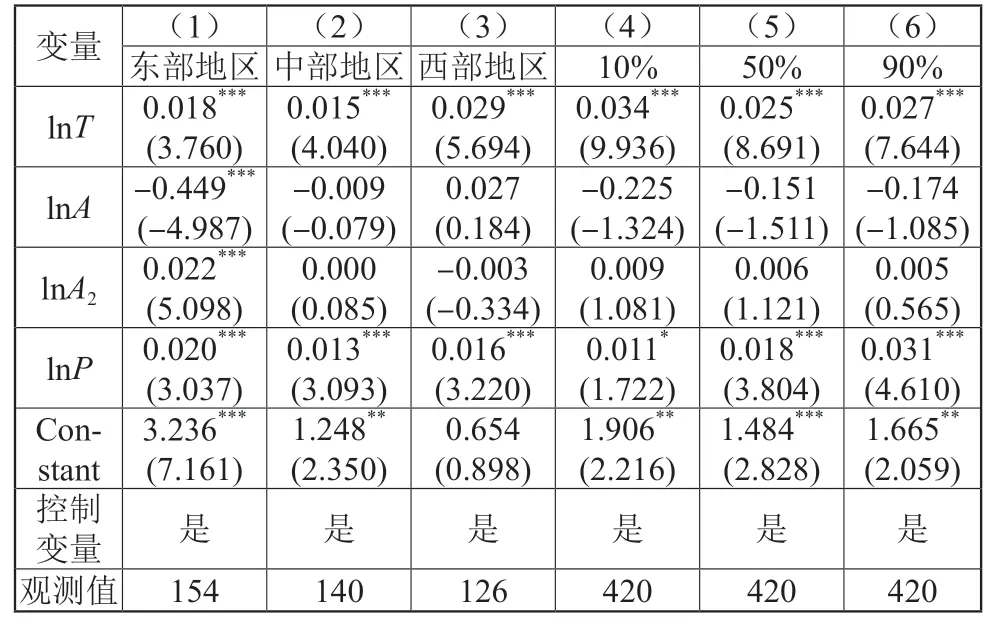
表4 异质性分析

分位数回归分析。实证结果表明科技创新对碳排放效率有正向促进作用，但是科技创新的促进作用是否会随着碳排放效率的不同而产生差异，以及这种影响的趋势如何变化？表4 第（4）、第（5）、第（6）分别是不同分位数下科技创新对碳排放效率的回归结果，10%用于阐述科技创新对低效率地区的影响，50%用于阐述科技创新对中效率地区的影响，90%用于阐述科技创新对高效率地区的影响。表4 显示，在10%、50%、90%的分位数水平下，科技创新对碳排放效率的回归系数均显著，且随着分位数的增加，科技创新的系数分别为0.034、0.025、0.027，呈现先下降后上升的趋势。这表明，科技创新对碳排放效率的条件分布的两端之影响大于其中间部分的影响。处于条件分布高端和低端的地区，科技创新的促进作用要高于平均水平，而且对于处于条件分布低端的地区，科技创新对碳排放效率的促进作用较高，即科技创新对于高碳排放效率和低碳排放效率的影响较大，碳排放效率水平居中的地区受益最小。这是因为高碳排放效率地区处于较高起点，拥有较高的技术水平、已经积累了一定经验，形成学习曲线，随着时间的积累，科技创新的促进作用更加明显。

4.4 稳健性检验

改变自变量度量方式。本文将采用以技术市场交易额来度量科技创新水平，并利用式（5）重新进行检验。结果见表5 第（1）、第（2）列，即使更改自变量的度量方法，科技创新水平的回归系数均在1%的水平上显著为正，与本文的研究结论保持一致。

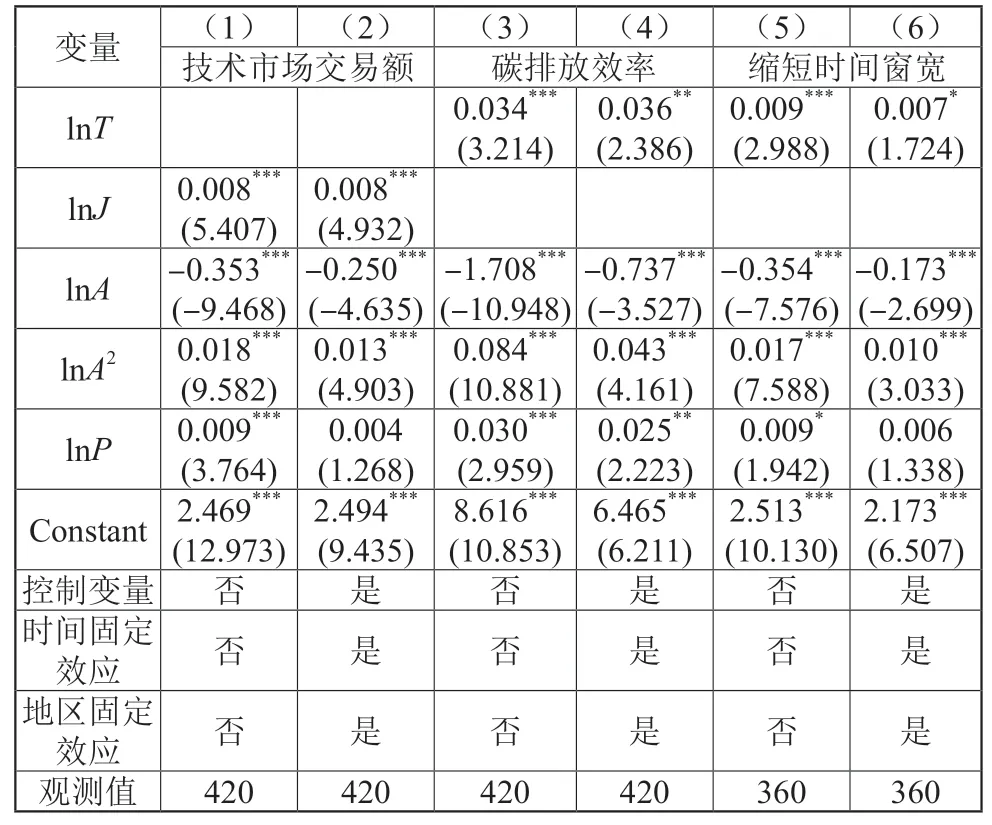
表5 稳健性检验

改变因变量度量方式。根据非径向的非期望产出SBM 模型重新测算规模报酬不变情况下的碳排放效率，并利用式（5）重新进行检验。结果见表5 第（3）、第（4）列，即使更改因变量的度量方式，科技创新水平的回归系数均显著为正，与本文的研究结论保持一致。

缩短时间窗宽。将时间区间缩短至2006—2017 年，重新对式（5）进行检验，回归结果见表5 第（5）、第（6）列，结果表明科技创新的系数依然显著为正，与本文的研究结论保持一致。

5 主要结论与政策建议

本文主要得到以下几点结论：（1）2005—2018 年，将30 个省份样本作为一个整体，其碳排放效率整体处于不断上升的趋势，碳排放效率从2005 年的0.859 2 上升为2018 年的0.896 3，碳排放问题得到明显改善。将30 个样本分为东、中、西三个区域，结果显示三个区域的碳排放效率总体上也呈上升趋势，但是碳排放效率的特征及其随时间的变化存在明显的差异。比较而言，东部地区的碳排放效率水平最高，其碳排放效率的最小值为0.882 7，最大值为0.939 7，西部地区的碳排放效率水平较低，其碳排放效率的最高值为0.855 0，远小于东、中部地区（中部地区碳排放效率的最小值为0.877 6）。（2）基准回归结果表明，科技创新对碳排放效率有显著的促进作用，且西部的科技创新水平对碳排放效率的正向促进作用明显高于东部地区和中部地区。（3）机制分析表明，能源利用效率提升是科技创新促进碳排放效率的重要途径，且中介效应在总效应中所占比例为43.85%。（4）科技创新对碳排放效率的条件分布的两端之影响大于其中间部分的影响，即提高科技创新水平对于高碳排放效率和低碳排放效率的影响较大，碳排放效率水平居中的地区受益最小。

碳排放效率提升的关键环节是提高科技创新水平。要贯彻落实“创新、协调、开放、绿色、共享”的新发展理念，坚持创新在中国现代化建设全局中的核心地位，打好关键核心技术攻坚战，提高科技创新水平，重视科技创新生态价值。政府加大地区科技研发投入强度，加强对核心低碳技术的开发，大幅提高科技成果转移转化成效，促进研发成果在能源利用、生态环境保护等方面实现产业化规模化应用。同时，政府应开展跨部门合作，加强环境监管，鼓励企业使用清洁技术提高能源利用效率，淘汰或升级高能耗、高污染企业。从长远角度来看，应该深化经济体制转型为切入点，扶持低碳产业和第三产业，提高产业链中利益相关者的清洁能源技术，逐渐走出高碳路径依赖的困境。鉴于所研究的地区之间在碳排放效率水平上存在明显的差异，环境和能源政策应该对每个地区在独特的技术和创新条件下足够灵活。