基于恒速压汞和核磁共振测井的低孔低渗储层变胶结指数确定方法
张建升,许赛男,齐 奕,时新磊
(中海石油(中国)有限公司 天津分公司,天津 300459)
引 言
胶结指数受孔隙结构、温压系统和泥质含量等多种因素的控制[1]。低孔低渗储层由于非均质性强、地质成因复杂[2-3],地层胶结指数的变化范围非常大[4]。现阶段胶结指数m的计算主要有以下几种方法:①利用岩电实验数据,根据阿尔奇第一公式直接得到,这是最基本的方法;②建立地层因素F与孔隙度之间的关系,得到m与孔隙度的函数[5-6];③直接建立m值与某些地质参数(阳离子交换容量Qv[6-7]、温压系统[8]、孔隙比表面积[9]等)的拟合关系,进而获得胶结指数;④通过豪斯道夫测度理论,计算测井曲线的分形维数,根据曲线分形特征给出m的计算公式[10];⑤基于理论推导得到胶结指数的表达式[11]。利用岩电实验直接得到胶结指数(常数)或拟合得到胶结指数与孔隙度的关系,易于操作且精度一般能满足应用,是目前最常用的方法。其他几种方法由于包含利用测井曲线无法获得的参数,且理论基础过于繁琐,所以只在某些区域得到一定的应用。
本文认为在低孔低渗砂岩储层中,孔隙和喉道对岩石导电起到不同的作用:在孔隙-喉道单元内部,孔隙和喉道串联导电,喉道之间并联导电;在相互独立的孔隙-喉道单元之间,孔隙-喉道单元并联导电。基于该假设建立低孔低渗砂岩导电模式,推导出了低孔低渗储层胶结指数模型。将该模型应用于其他油田的取心井中,获得了很好的应用效果。
1 低孔低渗储层胶结指数公式推导
假设存在一块横截面积为A,长度为L的低孔低渗砂岩,如图1所示。该砂岩存在n条孔隙-喉道单元,单条孔隙喉道单元中,孔隙的横截面积为Ap,半径为rp,孔隙长度为lp,喉道的横截面积为At,半径为rt,喉道长度为lt。
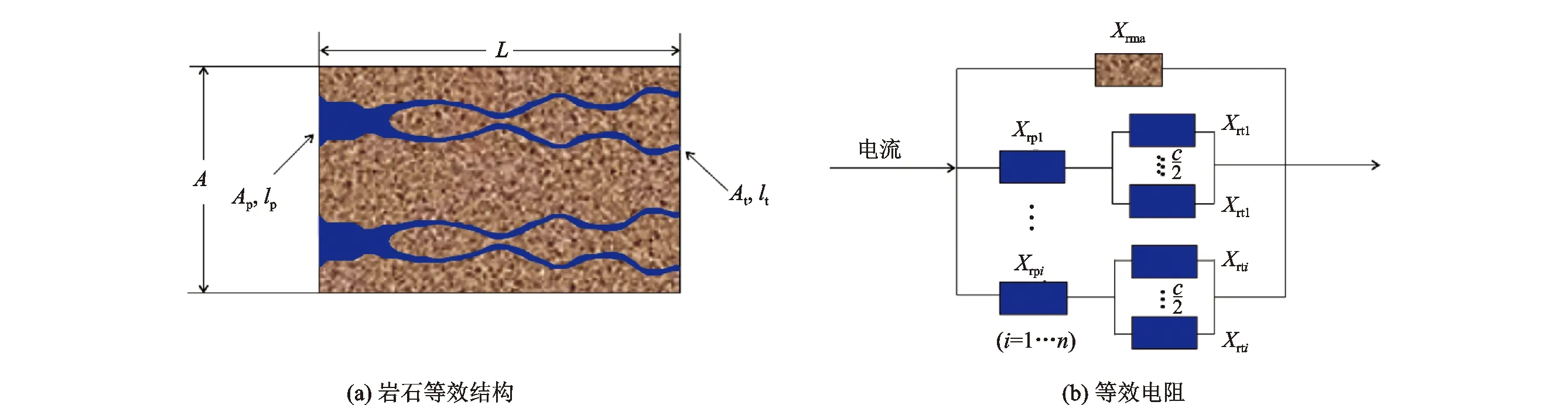
图1 低孔低渗砂岩等效模型Fig.1 Equivalent model of low porosity and low permeability sandstone reservoirs

单条孔隙-喉道单元中,孔隙和喉道串联连通砂岩的单条导电通道,所以其电阻可以表示为
(1)
相互独立的孔隙-喉道单元之间,孔隙-喉道单元并联导电。根据电阻并联导电的原理,可以得到饱含水的低孔低渗砂岩电阻为
(2)
借鉴等管径毛细管束模型理论,假设低孔低渗砂岩的孔隙-喉道单元具有相同的管道长度和管径,根据欧姆定律,低孔低渗砂岩的电阻可以表示为
(3)
式中,R0为饱含水低孔低渗砂岩的电阻率,Ω·m;rp,rt分别为孔隙和喉道半径,106μm。
对式(3)进行转化,可得
(4)
根据哈根-泊肃叶定律,单条孔隙-喉道单元单位时间内流量[12]可以表示为
(5)
式中,q为单条孔隙-喉道单元单位时间内的流量,m3/s;μ为流体黏度,Pa·s;Δpt为喉道两端的压差,Pa;Δpp为孔隙两端的压差,Pa。
令低孔低渗砂岩储层两端的压差为Δp,则Δp可以表示为[12]
Δp=Δpp+Δpt。
(6)
由式(5)和式(6)可得
(7)
该低孔低渗砂岩的总流量为
(8)
另,根据达西定律,砂岩流量可以表述为
(9)
式中,Q为通过低孔低渗砂岩储层的渗流流量,m3/s;K为低孔低渗砂岩储层的渗透率,m2。
由式(4)、式(8)和式(9),可得
(10)
式中,rpt为低孔低渗砂岩的孔喉半径比,无量纲。
前人研究表明,低孔低渗储层中孔隙半径远大于喉道半径,孔隙长度远小于喉道长度[13-14]。由rp≫rt,lp≪lt,可将式(10)近似转化为
(11)
根据阿尔奇第一公式,饱含水砂岩电阻率与地层水电阻率的比值可以表示为
(12)
式中,φ为孔隙度,小数。
将式(11)和式(12)联立,可得低孔低渗砂岩胶结指数的表达式
(13)
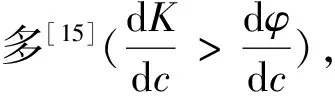
2 实例分析
以渤海湾盆地Q油田取心井Q3井为例,利用上述模型对胶结指数进行计算,并利用该胶结指数对计算出的饱和度进行精度验证。
2.1 参数求取
式(13)中涉及到的参数为孔隙度、渗透率和平均喉道半径。储层的孔隙度和渗透率参数可以通过核磁共振测井计算,故获得地层胶结指数的关键是储层喉道半径的准确求取。
2.1.1 恒速压汞资料计算喉道半径
自1989年Yuan等人提出速度控制压汞法以来,利用恒速压汞技术对喉道和孔隙的大小及分布进行表征,成为刻画岩石微观孔隙结构特征的常用手段。汞在压力作用下进入岩石,毛管和喉道半径r与进汞压力pc、汞在颗粒表面润湿角θ和表面张力σ间满足Washburn方程[16],即
(14)
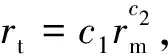

图2 平均喉道半径与平均毛管半径关系Fig.2 Relationship between average throat radius and average capillary radius
将式(13)进行转化,可得低孔低渗砂岩胶结指数与平均毛管半径的关系为
(15)
2.1.2 核磁共振测井资料计算平均毛管半径
利用常规压汞数据可以较为准确地获得岩心的平均毛管半径,但无法得到连续的地层信息。针对该问题赵文杰[17]提出了利用核磁共振曲线T2几何平均值重构平均毛管半径的方法,成功实现了平均毛管半径的连续计算。
通过Q3井取心段核磁-压汞联测实验数据(图3),得到目标区平均毛管半径的表达式
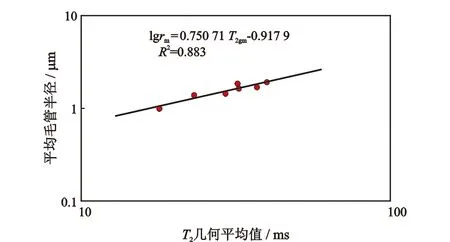
图3 平均毛管半径与T2几何平均值关系Fig.3 Relationship between average capillary radius and geometric mean of T2
lgrm=c3lgT2gm-c4。
(16)
式中,T2gm为T2几何平均值,ms;c3、c4为拟合系数,无量纲。
将式(16)代入式(15),即可实现胶结指数的连续计算。
2.2 模型应用
图4为渤海湾盆地Q油田Q3井东三段低孔低渗砂岩油层变胶结指数及含水饱和度处理结果。图中砂体在该油田稳定分布,孔隙度为7.3%~16.7%,空气渗透率为(0.06~11.8)×10-3μm2;岩性以细砂岩、中-粗砂岩为主,岩石致密,颗粒支撑方式,胶结类型为孔隙-接触式胶结。目标砂体黏土含量低(表1),质量分数含量为1%~3%,可以忽略黏土附加导电的影响。
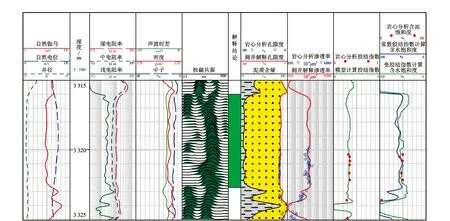
图4 渤海湾盆地Q油田Q3井变胶结指数及含水饱和度处理结果Fig.4 Variable cementation exponent and water saturation of well Q3 in Q oilfield of Bohai Bay Basin
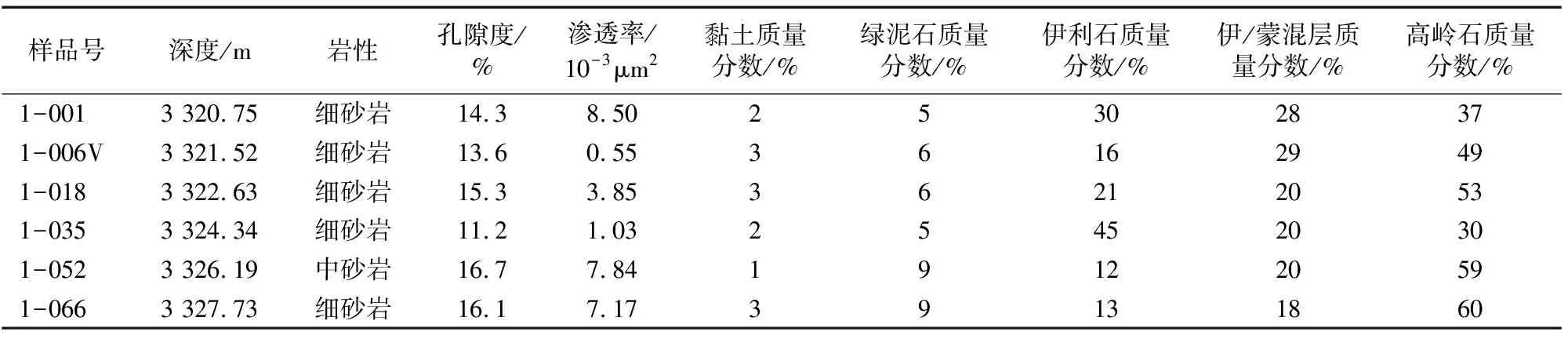
表1 低孔低渗砂岩岩性、物性及黏土矿物含量Tab.1 Lithology, physical properties and clay content of low porosity and low permeability sandstone reservoirs
从图4可以看出,模型计算的胶结指数与岩心分析胶结指数一致性较好,说明式(17)在低孔低渗砂岩储层胶结指数计算中具有较高的精度。利用Indonesia公式分别用常数胶结指数(m=1.633 8,n=2.130 4)和变胶结指数(n=2.130 4)计算了储层的含水饱和度,可以发现,在取心层段,变胶结指数计算的含水饱和度数值略低于常数胶结指数计算含水饱和度,且与常数胶结指数计算含水饱和度相比,变胶结指数计算含水饱和度与岩心分析饱和度吻合更好。
3 结 论
(1)在孔隙结构复杂的低孔低渗砂岩中,胶结指数m值不再为一个常数。基于孔隙-喉道单元组合导电模型,建立了m值与孔隙度、渗透率和平均喉道半径之间的函数关系。该模型在渤海油田具有很好的适用性。
(2)以恒速压汞实验数据为桥梁,实现平均毛管半径和平均喉道半径之间的转化,并依据核磁和压汞实验数据准确建立T2几何平均值与平均毛管半径的函数关系,是低孔低渗砂岩储层胶结指数获取、饱和度准确计算的基础。

