信息论在深度学习中的应用概论

摘要：信息论发展的80多年中在通信、计算机、统计等诸多领域取得了广泛应用;深度学习兴起的10多年间在图像识别、医学诊断、路线规划、语音识别等领域取得了巨大成功。最近几年，深度学习和信息论发展出了新的交叉学科，采用信息论的观点度量深度学习引发了学术界广泛关注。本文在总结深度学习和信息论领域之后分析了简单网络的互信息，提出星座图对互信息压缩的影响。

关键词： 深度学习;信息论;人工智能

中图分类号：TP393      文献标识码：A

文章编号：1009-3044（2022）11-0082-02

能够思考的机器长久以来都是人类的梦想。在中国，相传远古时期就有高度智能的七香车可以不要操控自动驾驶，“此车乃轩辕黄帝破蚩尤于北海，遗下此车，若人坐上面，不用推引，欲东则东，欲西则西——乃传世之宝也。”在国外，希腊神话中记载，皮革马利翁在雕刻人像时，精力和热情感动了神灵，人像获得了生命，能够思考和认知。

人类一直渴望用信息论[1]来度量机器学习（神经网络和深度学习[2]） ，1988年，Linsker首次提出“最大化信息量”的原则，并且用几个简单的例子进行证明。此后Van der Oord和Hjelm都在无监督学习领域进行了尝试。Shwartz-Ziv & Tishby，Saxe，Achille & Soatto对于深度学习进行了信息论分析。互信息在可逆映射下光滑不变，具有实际的物理意义和单位--比特，所以学术界一直渴望用互信息来度量机器学习。

1 深度学习发展历程

最近150年来，机器学习在图像识别、语音识别、医学诊断、路线规划等领域得到了广泛的应用，尤其是在抽象思维领域，机器学习取得了巨大的成功。最著名的案例当数1997年“深蓝”击败国际象棋世界冠军卡斯帕罗夫，然而抽象思维恰恰是计算机的特长，国际象棋具有明确的规则，棋盘共有64个深色与浅色相间的格子，每方十六枚棋子共计三十二枚，而且棋子的走法十分有限。设计国际象棋的算法是基于简洁的规则描述，非常适合计算机运算。这也是人工智能最大的挑战，很多问题无法正式描述。

2016年，阿尔法围棋机器人击败多位世界冠军，围棋界公认阿尔法机器人已经超过人类的最高水平。围棋同样高度抽象，棋盘有361个点位，只有黑色白色两种棋子，可以简洁地向计算机描述。围棋比国际象棋复杂，于是也较晚才获得成功。阿尔法机器人的工作原理采用深度学习算法，最终版的埃尔法机器人已经彻底放弃了人类棋谱，通过自我博弈逐漸提高。深度学习大约有三个发展阶段：第一阶段，1940―1960年深度学习被称作cybernetics，1980―1990年深度学习被称作connectionism，2006年以来正式命名深度学习。

对于人类来说最为困难的，抽象、严格描述的问题对于机器却极为简单，计算机虽然早就在棋类上彻底击败人类，但是近年才在图像识别、语音识别上达到人类的一般水平。日常生活中人类形成了大量的主观和直觉的知识，无法严格描述。所以人工智能面临的巨大挑战就是如何向机器传递主观、直觉、不严格的知识。

然而早期的人工智能并没有广泛应用，面临的最大问题是特征选择的困难。比如一辆白色的马在黑夜中看起来是黑色的马，而且马的形状非常依赖于观察角度。再比如口音会非常影响语音，从原始素材中提取适当的特征非常困难。

深度学习[3]可以很好地解决上述问题。典型的深度学习模型仅仅是输入映射到输出的数学函数，看起来无解的问题，比如图像识别需要处理大量像素。深度学习通过把目标映射分解成多层的简单映射，引发了学术界高度的关注。深度学习把输入，比如像素，作为可见层，然后连接了大量的隐藏层，深度学习算法会从可见层中提取有用的信息到隐藏层。比如假设可见层是输入像素，第一个隐藏层可以对比相邻的像素来搜索图像中的“边”，第二个隐藏层可以搜索“角”，第三个隐藏层可以搜索物体的“部分”，以此类推，可以逐渐识别出物体。

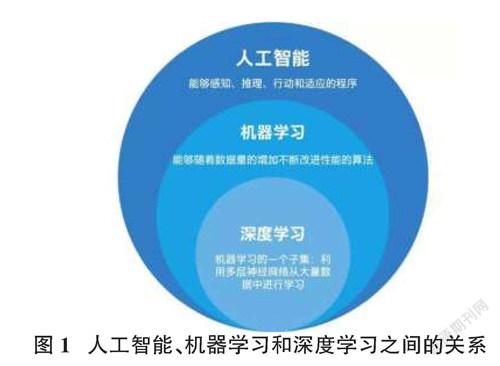
简单概括，人工智能中一种方法是机器学习，其中近年发展的部分是深度学习。深度学习用层次化的网络连接起不同的概念，抽象的概念建立在简单的概念之上，人工智能、机器学习、深度学习之间的关系如图1所示。

2 信息论发展历程

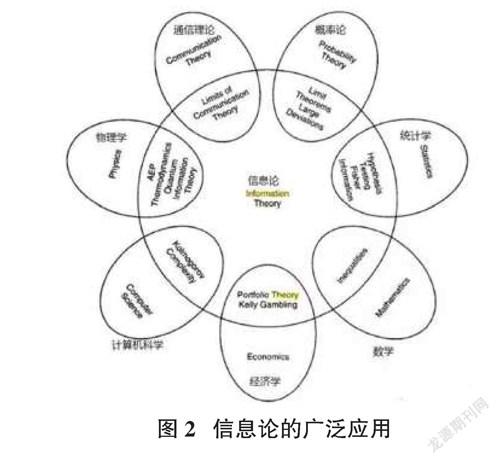
信息论主要解决两类问题，第一类是数据压缩速率，第二类是数据传输速率，所以很多人认为信息论是通信的分支，其实信息论的范围很广，对于热力学、计算机科学、统计学、概率论都有贡献。典型的量值中，熵是描述随机变量的最低复杂度，互信息是噪声通信的最大速率。

1940年左右，人们对苏通信中的误码率存在着较多误解，当时人们普遍认为增加传输速率必然提高误码率，降低误码率的唯一方式是增大信噪比。Shannon首次提出了信道容量的概念，信道容量只和信道的物理特性有关，通过编码可以实现信道容量内的任何速率。Shannon进一步提出任何随机过程，比如语音，都有熵作为本质属性，也是压缩的下限。只要熵不超过信道容量，几乎无差错的可靠通信可以实现。

随后拥有理论基础的信息论得到飞速发展，1950年发现汉明码，随后发现Fano码，Huffman码。1963年发现卷积的viterbi码。1973年发现Lempel-Ziv编码。1982年发现调制编码技术TCM。1993年发现turbo码，1998年发现时空编码。21世纪人们开始重新审视LDPC编码。随着人类计算能力的提高，LDPC码在实际中取得重大应用，接近信息论极值。信息论和多个领域都有交叉。信息论最初就是从电子工程的通信中诞生，通信中广泛地应用信息论。信息论又进而发展到网络信息论阶段，试图分析多点通信间的理论问题，虽然仍然缺乏完善的理论。

3 信息论在深度学习中的应用

学术界很早就开始尝试信息论在深度学习中的应用。互信息具有优越的特性：可逆映射下光滑不变，具有实际的物理意义和单位--比特。但是同时也有巨大的缺陷：解析的计算互信息是几乎不可能，而从样本中估计互信息也很困难。

所以学术界普遍采用了分集的方法来简化计算，尤其在分集较少的情况下，计算效率很高。本文采用的方法是熵估计，用其他分布来逼近目标分布再用蒙特卡洛法数值计算。在2017年Shwartz-Ziv & Tishby提出了信息瓶颈的观点，认为神经网络的训练会引起互信息的压缩降低。然而，确定性神经网络中，采用常用函数比如tanh和sigmoid，互信息是常数或者无穷，所以Shwartz-Ziv&Tishby观察到的波动很有可能是测量误差。

面对如此严峻的困难，可以选择最简单的例子进行探索。假设只有一个神经元，输入为[X=X-⋃X+={-3，-1，1，3}，X-={-3}，X+={-1，1，3}]，输出为Y，噪声为Z。噪声Z如从高斯分布[Z～N（0，β2）]，采用tanh（）函数则Y=tanh（wkX+b）+Z，那么网络中的信息量[I（X，Y）=I（X，tanh（wkX+b）+Z）=I（tanh（wkX+b），tanh（wkX+b）+Z）]正是高斯信道下的传输速率，星座點分别为[X-，X+]对应的[tanh（wkX+b）]。星座点之间距离越大则高斯噪声产生的干扰越小，星座点之间距离越小则高斯噪声产生的干扰越大。起始状态w=0，四个星座点完全重叠，然后采用均方误差和0.02的梯度进行神经网络的训练，随着训练次数的增加，星座逐渐分开，互信息逐渐增加，在两千次训练后互信息达到峰值随后开始下降，因为星座点开始重合。因而星座图会影响互信息的压缩。

4 结论

深度学习和信息论领域发展多年后产生了学科交叉，采用信息论的观点度量深度学习引发了学术界广泛关注。本文在总结深度学习和信息论领域之后分析了简单网络的互信息，提出星座图对互信息压缩的影响。

参考文献：

[1] （美）ThomasM.Cover，（美）JoyA.Thomas.信息论基础[M].阮吉寿，张华译.北京：机械工业出版社，2008.

[2] 邱锡鹏.神经网络与深度学习[M].北京：机械工业出版社，2020.

[3] 焦李成，杨淑媛，刘芳，等.神经网络七十年：回顾与展望[J].计算机学报，2016，39（8）：1697-1716.

收稿日期：2021-05-30

作者简介：郭扬（1988—） ，男，江苏徐州人，讲师，硕士，主要研究方向为人工智能、教育学。