基于探地雷达的田块尺度下不同深度土壤含水量监测

张文瀚 杜克明 孙彦坤 刘布春 孙忠富 马浚诚 郑飞翔

摘要：为确定田块尺度下探地雷达对不同深度及相邻反射层间土壤含水量的反演精度、有效反演深度、最佳反演深度及最优反演模型，本研究采用1000 MHz 中心频率探地雷达设备，分别在无降雨偏干旱土壤和降雨后湿润土壤两种条件下，在选定农田区域基于共中心點法采集雷达波数据，提取有效地表波与反射波数据，通过双曲线拟合法分别获取不同深度反射层雷达波的传播速度，计算得出土壤的相对介电常数，最后根据土壤体积含水量和介电常数之间的经验模型计算获得不同深度的土壤体积含水量。通过Topp、Roth、Herkelrath和Ferre四种经验模型分别进行土壤体积含水量反演测定，同时以利用烘干法获取的代表性测定土壤含水量实测值为指标进行精度验证。田间试验结果表明，1000 MHz 探地雷达的有效反演深度范围为0～50 cm;土壤偏干旱和偏湿润条件的最佳反演深度分别为50 cm 和40 cm; Roth 模型相关性最好，决定系数 R2最高为0.750，且 Roth 模型反演土壤含水量值最稳定，在土壤偏干旱和偏湿润条件下均方根误差（ Root Mean Square Error ，RMSE ）平均值分别为0.0401 m3/m3和0.0335 m3/m3;相对误差（Relative Error ，RE ）最低为3.0%。探地雷达具备对定量深度田间土壤含水量快速、精准监测的能力，但其反演模型需根据不同土壤类型等条件进行相应参数校正。

关键词：探地雷达;土壤含水量监测;共中心点法;最佳反演深度;最优反演模型;Roth 模型

中图分类号：P412.25;S152.7         文献标志码：A               文章编号：SA202202010

引用格式：张文瀚， 杜克明， 孙彦坤， 刘布春， 孙忠富， 马浚诚， 郑飞翔.基于探地雷达的田块尺度下不同深度土壤含水量监测[J].智慧农业（中英文）， 2022， 4（1）：84-96.

ZHANG Wenhan， DU Keming， SUN Yankun， LIU Buchun， SUN Zhongfu， MA Juncheng， ZHENG Feixiang. Moni‐toring specified depth soil moisture in field scale with ground penetrating radar[J]. Smart Agriculture， 2022， 4（1）：84-96.（in Chinese with English abstract）

1 引言

从全球水文循环来看，土壤水分总量较小且仅占全部水分总量的0.05%左右，但其对全球能量平衡和降水分布具有十分重要的意义[1]。土壤中水分含量的变化会对作物生长状况产生直接影响。特别在田块尺度上，土壤含水量是作物产量和品质的主要控制因素[2]。因而，有效精准地测定田间土壤水分含量对作物长势监测和产量预测具有重要意义。

现阶段，研究人员基于不同的需要，对于土壤含水量的测定已有较多的技术方案。传统测定土壤含水量的方法主要有烘干法、中子法以及时域反射法 （Time Domain Reflectometry ， TDR ）等。这些方法能较准确地测量指定位置的土壤含水量，但在实验操作中对田土具有破坏性。卫星遥感技术的出现打破了区域尺度大面积土壤水分动态监测的壁垒[3]，研究人员通过建立经验或半经验模型来提高土壤含水量的反演精度，但卫星遥感易受植被覆盖、天气条件等影响[4]，并且针对田块尺度下不同深度土壤含水量的监测，卫星遥感数据的分辨率、保障率和精度有待提高[5，6]。因此，田块尺度定量深度土壤含水量的高精度、快速无损测量成为目前研究的难点。

探地雷达（Ground Penetrating Radar ，GPR ）是近年来新兴的一种土壤水分监测技术手段，与众多土壤含水量探测方法相比，探地雷达具有操作简单、分辨率高、探测深度大、可重复性以及对地下非侵入性测量等优点。由于探地雷达具有上述优势且在测量过程中无需扰动作物与土壤，所以在田块尺度深层土壤含水量的测量方面表现出很大的潜力。综合国内外探地雷达研究现状，目前基于探地雷达和雷达波信号分析的土壤水分快速无损监测研究主要集中在以下3个方面[7，8]。

（1） 快速测定土壤表层含水量。Grote 等[9] 使用900 MHz和450 MHz探地雷达测量美国加州葡萄园表层土壤含水量，雷达反演值与烘干法实测值相关性较好，证明了探地雷达地表波可以快速、无破坏性地提供大面积土壤表层含水量。Galagedara等[10]使用探地雷达和6个不同长度的时域反射仪，在沙壤土上设计排水试验探究探地雷达的有效反演深度，结果表明100 MHz探地雷达在0～0.1 m深度反演结果较精确。

（2） 不同地质类型的土壤含水量反演。Al‐ geo等[11]使用探地雷达振幅分析法监测粘性土壤中土壤含水量对灌溉的响应变化，试验结果表明该方法可以获取富含粘粒土壤中地下含水率的空间分布信息。王前锋等[12]利用宽角反射与折射法 （Wide  Angle  Reflection  and  Refraction，WARR ）和固定间距法（ Fixed Offset ，FO ）相结合证明了200 MHz中心频率天线在沙漠地区地波法的最佳天线间距为1.9 m ，有效深度为20 cm，偏差仅为0.015 m3/m3。曹棋等[13]利用探地雷达地波法证明了60 MHz 天线在红壤地区反演0～40 cm 土层的土壤体积含水量时精度最高，Roth经验模型更适合于红壤地区，均方根误差（ RootMean Square Error ，RMSE ）为0.022 m3/m3。

（3） 土壤含水量反演模型建立及参数校正。李蕙君和钟若飞[14]利用探地雷达探究土壤介电常数与雷达回波振幅之间的变化规律，建立了探地雷达波振幅与土壤介电常数之间的定量关系，模型反演精度较高，RMSE 为0.014 m3/m3。Cao等[15]利用探地雷達探究了地表至1 m 深的三维土壤水分变化以及降雨事件对土壤水分空间动态的影响，并每间隔20 cm建立了介电常数与土壤体积含水量的反演模型。

目前大部分研究主要侧重在不同地质类型的土壤含水量反演以及经验模型的校正，基于田块尺度的不同深度土壤层含水量反演的相关研究较少，实验数据尚不充分。然而，在田块尺度下，不同深度土壤层水分对作物的生长会产生相应不同的影响[16]，能否快速、无损地对不同深度土壤层含水量进行监测对于田间精准灌溉、作物生长监测、作物品质与产量预测等方面起到重要作用。

因此，为确定田块尺度下探地雷达对不同深度及相邻反射层间土壤含水量的反演精度、有效反演深度、最佳反演深度及最优反演模型，本研究采用1000 MHz中心频率探地雷达设备，分别在无降雨偏干旱土壤和降雨后湿润土壤条件下的标准农田环境，反演不同深度土壤体积含水量，并与对应取样土壤烘干法实测值进行对比验证。同时，利用雷达波从地表传播至不同深度反射层的平均速度和迪克斯（ Dix ）公式，探究探地雷达对相邻反射层间土壤水分的反演精度。

2 材料与方法

2.1研究区概况和试验设备

研究区位于北京市顺义区大孙各庄镇中国农业科学院农业环境与可持续发展研究所试验基地。顺义区年均降雨量约625 mm ，全年降水的75%集中在夏季。试验选取研究区的50 m×20 m 试验农田，农田土壤以潮土、褐土为主，作物常年为小麦、玉米轮作。试验期间农田无作物种植，雷达移动路径为裸露地表且地表较平整，适宜进行雷达试验等。

试验采用加拿大 Sensor & Software公司生产的 Pulse EKKO PRO 型探地雷达，由主机、发射天线 （ Transmitter ， T ）、接收天线（ Receiver， R ）、电池及其连接装置构成，其中两个天线频率均为1000 MHz 。其它试验设备为50 m卷尺以及烘干法采集土样所需的土钻、环刀、标签、铝盒等。

2.2试验方法

2.2.1 探地雷达测量土壤含水量的原理

探地雷达发射天线向外发射高频电磁波，部分电磁波通过空气直接从发射天线传播到接收天线，这些电磁波称为空气波（ Air Wave ，AW ）。地表波（ Ground Wave ， GW ）沿着土壤表面传播到接收天线，其路程可近似看作两个天线之间的间距。

反射波（ Reflected Wave ，RW ）或折射波穿过地表到达地下介质，当电磁波遇到电性差异大的分界面、目标体或者具有不同介电常数的材料时，探地雷达电磁波的振幅、频率和相位都会发生变化，从而发生散射和反射，并从不同的界面返回接收天线。随后，接收天线接收各种电磁波，根据探地雷达电磁波的双程走时、相位、振幅等参数，可以确定地层结构或目标体的埋深、位置等[17]。

电磁波在介质中传播速度取决于光在真空中传播速度、相对介电常数（ε） 和相对磁导率[18]。雷达波在非饱和带土壤中的传播速度与土壤的介电常数密切相关。常温下，土壤固相的相对介电常数大约是3～10，空气的相对介电常数是1，淡水的相对介电常数是81，淡水的相对介电常数远大于空气和干土壤的相对介电常数。因此，非饱和土壤的介电常数主要依赖于土壤含水量[19，20]。根据雷达波传播速度与介电常数之间的关系式（公式（1） ），可以计算出土壤的相对介电常数ε[21，22]：

（1）

其中，v为雷达波在土壤中的平均速度，m/ns;c为自由空间中电磁波传播速度，0.3 m/ns。

因此，可以利用共中心点法雷达剖面图像提取出雷达波在土壤中的传播速度，通过公式（1）获得土壤的相对介电常数，最后根据土壤体积含水量和介电常数之间的经验模型或半理论关系式获得土壤体积含水量。

为描述介电常数ε与土壤体积含水量θ之间的关系，研究者们已经提出了很多经验模型，其中Topp模型[23]、  Roth 模型[24]、Herkelrath模型[25] 以及Ferre模型[26] 因其变量少、表达式简洁、相关性好而被广泛应用，故本研究采用这4个模型对土壤含水量进行反演。模型表达式见公式（2） ～公式（5）。

Topp模型：

θ=-0.053+0.0292ε-0.00055ε2 +

0.0000043ε3                                        （2）

Roth模型：

θ=-0.0728+0.0448ε-0.00195ε2 +

0.0000361ε3                                        （3）

Herkelrath模型：

θ=-0.1626+0.1117              （4）

Ferre模型：

θ=-0.1841+0.1181             （5）

2.2.2 共中心点法

共中心点法（Common Midpoint ，CMP ）是在待测点确定后，将探地雷达发射天线与接收天线以待测点为中心位置水平放置，并同时向相反的方向等距离移动的测量方法（图1（a））。共中心点法可以有效地提高探地雷达图像效果。当使用共中心点法收集雷达数据时，由于中心位置不变，雷达波的叠加提高了地下雷达反射的信噪比，从而使雷达剖面图像更清晰[27，28]。

试验中雷达收发天线每次分别向左右移动0.01 m ，移动距离的总长度为2 m 。CMP雷达图像是由100道雷达数据组成（图1（b）），每一道雷达数据表示在相同的天线间距下，雷达波在介电常数不同的反射层发生反射，分別以不同的双程旅行时间被接收天线获取，并在主机中以图像形式记录。100道雷达数据组成雷达图像中的若干条灰色曲线，从图像中可以清晰拾取地表波与空气波。由于表层土壤反射层较浅，且雷达发射天线与接收天线距离较小，因此地表波在雷达图像中表示为一条直线，其斜率代表地表波的波速。空气波是雷达波从发射天线经由空气直接由接收天线接收，由于电磁波在空气中的速度大于在土壤中的速度，因而最先被接收天线获取，所以在雷达图像中以第一条直线表示，理论上其速度值接近0.3 m/ns 。本研究雷达图像未能完全将空气波捕获，文中的空气波仅代表雷达波通过与空气接触的浅表层土壤的雷达图像，但本研究并未应用空气波的相关性质，因此对试验结果不造成影响。

雷达图像中地表波以下的每条曲线代表介电常数不同的层间反射，即为反射波，其反射曲线的曲率代表反射波的传播速度。由于土壤反射层相比地表深度较大，因而不能忽略反射层深度对雷达波传播距离的影响，即不能将雷达波运动过程视为雷达天线间距。图1（c）为反射波在土壤层中的传播过程，其中 d表示反射层距离地表的垂直深度，m; x 代表雷达天线间的水平距离，m ; v 代表反射波在土壤中传播的平均速度，m/ns ; t 代表反射波双程旅行时间， ns 。根据图1（c）雷达波双程旅行时间与天线间的水平距离的关系可知：

又因为 x >0，所以雷达反射波的图像在xt坐标系下是焦点在 t轴的双曲线的一半（取 t轴正半轴部分）。因此，本研究在获取测点不同深度反射层的反射波速度时，应用双曲线拟合法直接从软件读取，而不通过计算反射波图像近似直线的斜率获得，双曲线拟合图像如图1（b）反射波所示。

通过上述方法获取的速度值代表雷达波从地表传播至不同深度反射层的平均速度值，其反应了地表至不同深度反射层的平均含水量。若想分别反演不同深度相邻反射层间土壤体积含水量，需获取雷达波在土壤相邻反射层中移动的速度，因此本研究尝试采用 Dix 公式[29]将雷达波至反射层的平均速度转换为雷达波在相邻反射层间移动的层速度，其表达式如公式（8）。

其中，vsoil，n 为第 n 个反射层之上的平均波速，m/ns ;tRW，n 为第 n 个反射层的反射波旅行时间，ns ;vsoil，n -1为第 n-1个反射层之上的平均波速，m/ns ;tRW，n -1为第 n-1个反射层的反射波旅行时间，ns。

2.3数据采集与处理

试验数据采集共分为雷达数据和不同深度土壤样本两部分。其中，雷达数据和土壤样本采集均两次，第一次数据获取在2021年6月28日至7月1日，试验期间无降雨事件，最高温度为33℃;第二次数据获取在2021年10月12日至15日，试验前两天内有少量降雨，田间土壤湿润。并且两次取样位置相同，雷达数据与土壤样本数据一一对应。

在试验农田间隔5m平行布置三条50m长的测线，由测线端点开始每间隔8 m插上地标，作为土壤烘干法取样点。用环刀与土钻在每个取样点处取0～10 cm 、10～20 cm 、20～30 cm 、30～40 cm 、40～50 cm 和50～60 cm 六个不同深度土层的样本，密封并做好标记后放置烘箱中105℃烘烤12小时，待烘箱内冷却至室温后取出，称重并计算不同深度土壤层体积含水量。由于土钻取样过程是在同一测点的连续10 cm 深度取样，因此分别将同一测点不同深度的土壤层体积含水量取平均值计算0～10 cm 、 0～20 cm 、0～30 cm 、0～40 cm 、0～50 cm 和0～60 cm 土壤体积含水量。

探地雷达 CMP数据采集以烘干法取样点作为中心点，无降雨偏干旱土壤和降雨后湿润土壤条件下各采集15幅雷达图像。使用探地雷达数据处理软件EKKO_Project对雷达数据进行增益、滤波等处理，有利于雷达波的提取和识别。地表波的速度由地表波所在直线的斜率获取，反射波的速度由双曲线拟合法从软件中直接读取，将获取的速度值分别带入公式（1），进而求得地表至不同深度反射层土壤的相对介电常数，结合常用模型（公式（2） ～公式（5） ）可以获得相应的土壤体积含水量模型预测值。将4个模型的不同深度土壤体积含水量模型预测值分别与对应深度土壤烘干法实测值进行精度评价，依据精度评价结果判断探地雷达对不同深度土壤含水量反演精度、有效反演深度、最佳反演深度以及1000 MHz探地雷达田块尺度最优反演模型。采用 RMSE、R2、相对误差（ Relative Error ，RE ）和绝对误差（ Absolute Error ， AE ）对试验结果进行精度评价。同时，结合已从雷达图像中获取的地表波和反射波的速度值，利用 Dix公式将雷达波的平均速度转换为层速度，进而结合最优反演模型获取不同深度相邻反射层间的土壤体积含水量模型反演值。通过将模型反演值与土壤含水量烘干法实测值进行精度评价，探究探地雷达对不同深度相邻反射层间土壤含水量的反演精度。

3 结果与分析

3.1土壤体积含水量及雷达有效反演深度

两次试验 CMP测点的0～60 cm 不同深度土壤体积含水量烘干法实测值如图2所示。图像的中心点表示相同深度土壤样本体积含水量实测值的平均值，中心点处有色部分的垂直长度表示所在深度范围土壤体积含水量的标准差。图 2（a）中不同深度土壤体积含水量的标准差依次为0.03、0.02、0.02、0.01、0.01、0.01;图 2（b）中标准差依次为0.03、 0.02、 0.03、 0.02、0.02、0.02。

从图中可以看出，在无降雨条件下，田间表层0～10 cm土壤含水量偏低，样本最低土壤含水量为0.24。随着采样深度逐渐增加，土壤含水量逐渐升高，在60 cm 处最大值为0.31。本次试验前的降雨主要对表层土壤水分产生影响，0～10 cm 深度范围土壤含水量最大值为0.36。由于环刀采样时表层土壤水分没有完全下渗，因而随着深度的增加，土壤含水量整体呈降低趋势。

图3是两次雷达数据采集的 CMP 法雷达图像。其中图3（a）～图3 （c）为无降雨条件的 CMP 图像;图3（d）～图3 （f）为降雨事件后的 CMP 图像。为更清楚地获取不同采样条件下 CMP 图像特点，图 3所选三个测点均不在测线同一行、同一列，且两次试验 CMP 采集位置均相同。從图像中可以很容易发现，两次雷达图像的最大时延相差较小，表明雷达波在两次试验中最大探测深度非常接近。但从雷达波获取情况来看，在无降雨条件下，雷达波通过不同深度反射层所产生的反射波分层更明显。而降雨后受土壤中下渗水分影响，雷达图像在相邻反射层间容易出现杂波，具体表现为短小曲线，随着天线间距的增加，其杂波也随之消失。

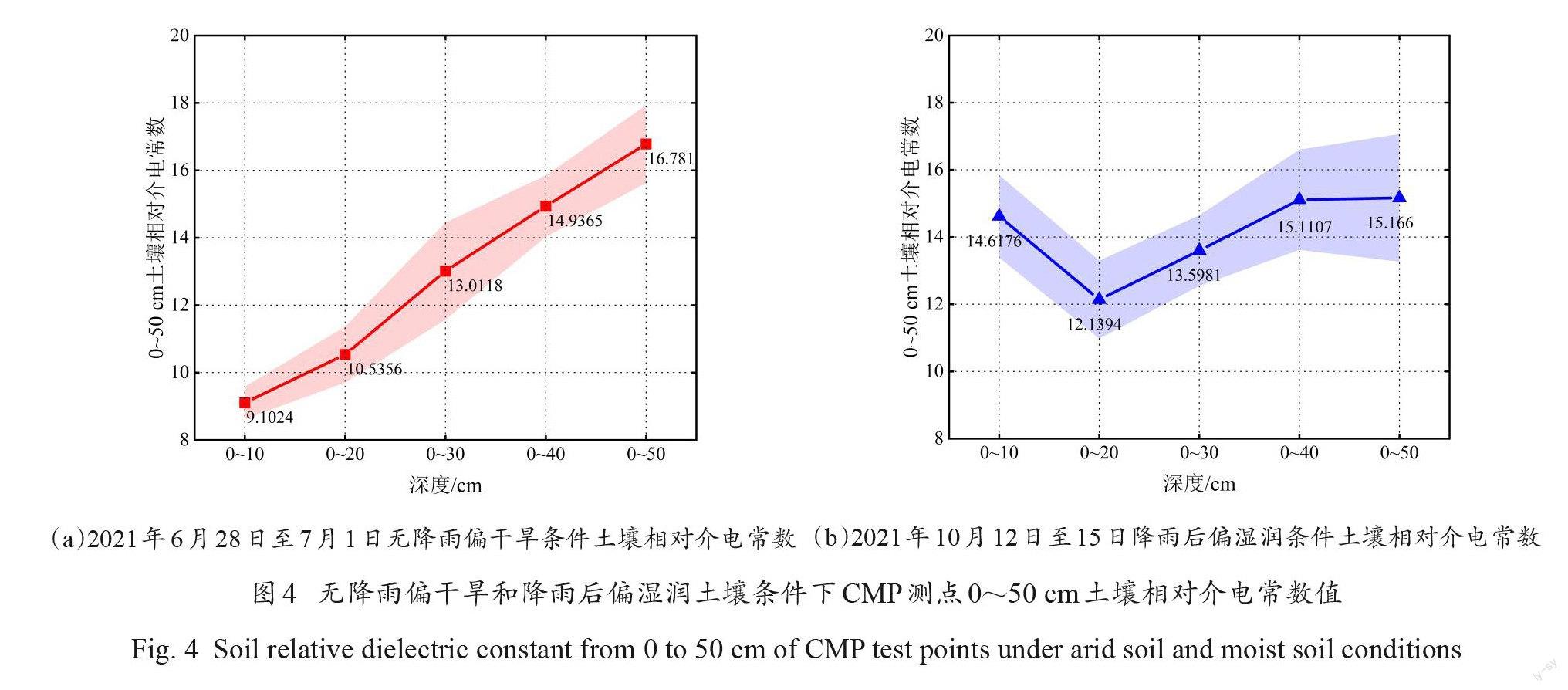
图4是两次试验利用 CMP法获取的测点处0～50 cm土壤相对介电常数分布图。中心点表示相同深度范围的土壤相对介电常数平均值，中心点处有色部分垂直长度表示相对介电常数的标准差。由于30个测点的 CMP 图像几乎在60 cm处无法获取明显反射层，并且雷达图像在50～60 cm 深度范围没有明显呈双曲线状的反射波，因此本研究后续土壤含水量反演精度仅讨论至50 cm。

图中0～10 cm深度范围的土壤介电常数由地表波斜率求得，0～20 cm至0～50 cm土壤介电常数由反射波双曲线拟合法在软件中直接读取。两种土壤水分条件下，不同深度土壤的介电常数值在分布图中分层明显，无降雨条件的土壤介电常数与土壤含水量实测值变化趋势一致，0～10 cm 土壤介电常数偏低，随着深度的增加介电常数值也逐渐增大。与无降雨条件相比，降雨后0～20 cm深度范围的土壤介电常数明显偏高，但与降雨后土壤含水量实测值变化趋势不同的是，0～20 cm至0～50 cm土壤相对介电常数随深度的增加逐渐增大。

相同深度范围土壤的介电常数在±3小范围内波动，说明地下相同深度的土壤反射层分布不均匀。因此在使用双曲线拟合法处理雷达数据时，其反射层深度值变化幅度在2 cm 左右均视为正常值，且对于在某一深度范围 CMP 图像中未有明显反射波的测点数据，在进行相关性分析以及后续 RMSE等精度验证时为了对整体精度验证结果不造成较大影响，在计算时应将图像中无反射波的深度范围对应土壤水分实测值同时删除。

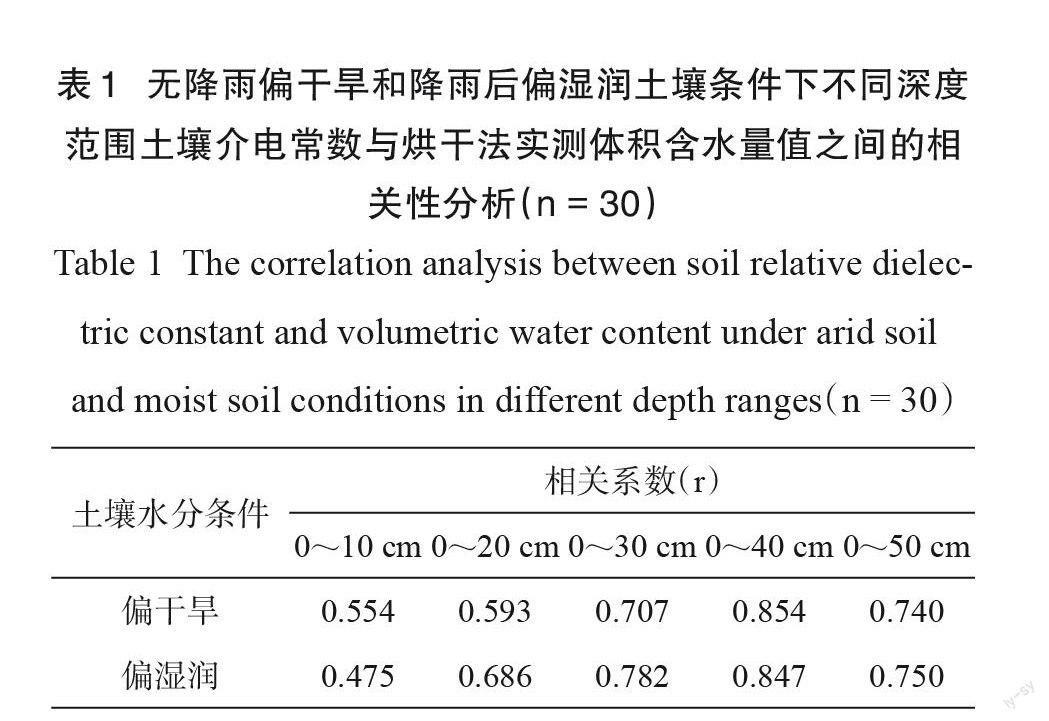
通过将不同深度土壤体积含水量实测值与对应深度范围土壤相对介电常数进行相关性分析发现（表1）。两次试验0～10 cm 深度范围的相关系数均较低，表明两次试验中雷达地表波对表层土壤介电常数的反演精度偏低，其原因可能是由于1000 MHz探地雷达的地表波有效代表深度的不确定性，导致实际土壤样本采样深度与地表波代表深度不匹配，从而造成误差。将两次不同土壤水分条件下的相关系数对比分析发现，降雨对相关系数的影响较小，相关系数均随着土壤深度的逐渐增加而逐渐增大，并在0～40 cm处达到最大值。同时，两次试验结果在0～50 cm深度范围均有较好的相关性，因而相关性分析结果表明1000 MHz 探地雷达在本次试验田块的有效反演深度为50 cm。

3.2田块尺度最优模型及最佳反演深度

通过雷达波图像获得的土壤相对介电常数结合Topp模型、Roth模型、Herkelrath模型和Ferre模型，即可得到土壤体积含水量的模型预测值。图5是1000 MHz 探地雷达分别在两种土壤水分条件下，不同深度土壤烘干法实测值与4个模型反演值的相关性对比图。其中，图 5（a）代表无降雨条件下的雷达反演精度，图中灰色十字代表在有效反演深度范围4个模型的最小 RMSE平均值，其所在位置代表在该深度范围具有最小RMSE的模型。

在无降雨条件下，Topp模型的相关性随着深度的增加而逐渐增大，相关系数在0～50 cm深度范围达到最大值（ R2=0.626）;其他三个模型的相关性变化趋势相同，均在0～40 cm深度范围达到最大值，其中 Roth 模型相关性最好（ R2=0.645）。而4个模型在0～10 cm 和0～20 cm 深度范围的决定系数较低（ R2在0.3上下浮动），在0～30 cm 深度范围开始显著增加。Roth 模型在0～10 cm 至0～40 cm 深度范围均具有最小的 RMSE ，而在0～50 cm 深度范围内Herkelrath模型 RMSE最小。在土壤湿润条件下，4个模型相关性变化趋势相同，Roth 模型在0～40 cm 深度范围相关性最好（ R2=0.750），并且在0～10 cm 至0～30 cmRMSE最小。

在有效反演深度范围内，通过对比两种土壤水分条件下4个模型反演值与实测值的 RMSE平均值 （表2）， Roth 模型在5个深度范围内的 RMSE平均值明显低于其它3个模型，表明 Roth 模型在有效反演深度范围内具有更稳定的反演能力。

图6是两种土壤水分条件下，有效反演深度范围内模型反演值与实测值的 AE 变化趋势图。从反演结果来看，4个模型的反演值普遍低于实测值。在无降雨条件下，随着深度的增加，模型反演误差逐渐降低。在0～10 cm 至0～40 cm 深度范围内，与其它模型相比 Roth 模型反演值的 AE 较低。0～50 cm 深度范围内，4个模型的 AE 较接近，Herkelrath模型 AE 最低， 0.02 m3/m3。在地表湿润条件下，4 个模型均在0～40 cm 深度范围误差最小。其中 Roth 模型在0～10 cm 至0～30 cm 深度范围 AE 最小，而在0～40 cm 和0～50 cm深度范围，Roth模型的反演值与实测值相比偏高。

此外，隨着土壤采样深度的逐渐增加，RE逐渐降低（表3）。在无降雨条件下，Roth 模型在0～10 cm 至0～40 cm 范围内 RE 最小;在0～50 cm 深度范围内，Topp模型 RE 偏大，其它三个模型 RE 值较接近。在土壤湿润条件下，4个模型的 RE均在0～40 cm深度范围内达到最小值;Roth 模型在0～10 cm 至0～30 cm 深度范围内与其它三个模型相比 RE最小，而在0～40 cm至0～50 cm深度范围内，其 RE较大。

因此，基于在两种土壤水分条件下的4个模型反演值与实测值的相关性分析及包括RMSE 在内的3种误差分析结果，本研究选定1000 MHz 探地雷达在试验田块的最优模型为Roth 模型。在无降雨条件下，最佳反演深度为50 cm ;在土壤湿润条件下，最佳反演深度为40 cm。

3.3相邻反射层间土壤含水量反演精度

利用雷达波通过不同深度反射层的速度值和Dix公式，获取雷达波在10～20 cm 、20～30 cm、30～40 cm和40～50 cm土壤层的层速度，并利用公式（2） 获取不同层间土壤的相对介电常数，再结合 Roth 模型获取不同深度相邻反射层间土壤含水量的模型反演值。模型反演值与实测值的精度验证如表4所示，无降雨条件下20～30 cm 深度范围误差最小，其余深度范围误差较大， RE 在40～50 cm 深度范围最高可达41.3%。降雨后土壤湿润条件下，4 个深度范围中仅在40～50 cm反演精度较高，并且10～20 cm至30～40 cm深度范围的反演精度随着深度的增加，误差逐渐增大，其结果与0～10 cm 至0～40 cm 深度范围的反演结果相反。

因此，依据本次试验结果可以看出，利用探地雷达及 Dix公式对不同深度相邻反射层间土壤水分的反演具有局限性，其反演精度有待进一步加强。无降雨条件下，对层间土壤的反演精度更高;然而，对于从地表至反射层间土壤水分的反演精度来说，无降雨条件的反演精度低于降雨后土壤湿润条件下的反演精度。由此可见，降雨对探地雷达的反演精度产生一定的影响，其原因一方面可能是由于降雨后表层土壤水分未完全下渗造成反演误差;另一方面， Roth 模型是基于TDR 在实验室中建立，对于本次试验结果造成较大误差可能是其对于农田环境的层间土壤水分反演的适用性不强所致。

4 讨论

本研究通过设置探地雷达 CMP法田间土壤水分监测试验，期望探究探地雷达对不同深度及相邻反射层间土壤含水量的反演精度。分析雷达波速度及介电常数，结合RMSE 、R2、AE和 RE ，确定田块尺度最优模型、雷达波有效反演深度以及两种土壤水分条件下的最佳反演深度。

分析雷达波对不同深度土壤水分的监测精度，反射波对土壤含水量的反演精度高于地表波。可能由于试验田块表层土壤受耕作过程等影响，其土壤状态易被破坏，导致地表0～10 cm土壤样本实测值与地表波反演值出现较大偏差。通过观察两种土壤水分条件下的雷达图像，试验田块深层土壤有明显的反射层，并且空间变异性较小，表明双曲线拟合法可以得出较准确的波速值。但是雷达图像能否存在明显的反射波取决于地理位置及土壤类型，前人研究表明在没有明确地下反射层的条件下，地表波法仍然是测定浅表层土壤含水量的有效方法[30]，今后应加强探地雷达在不同土壤类型的有效反演深度探究和地表波的反演精度。

土壤含水量模型精度影响探地雷达的反演精度，本次试验得出 Roth 模型是田块尺度最优反演模型。但 Roth 模型的参数是基于时域反射法和土壤样本于实验室建立，与农田环境差别较大。在不同试验区域若想提高探地雷达的反演精度，需要依据试验区实际土壤水分情况对 Roth 模型参数进行校正。

5 结论

为确定田块尺度下探地雷达对不同深度及相邻反射层间土壤含水量的反演精度、最优反演模型、有效反演深度及最佳反演深度，本研究在无降雨偏干旱和降雨后偏湿润两种土壤水分条件下各选取15个测点，采用1000 MHz中心频率探地雷达，进行 CMP法测定土壤体积含水量。将4种模型反演值与烘干法实测值进行精度验证后得出结论：

（1） 1000 MHz 探地雷达的有效反演深度范围为0～50 cm;在土壤偏干旱条件下最佳反演深度为50 cm ，在土壤湿润条件下最佳反演深度为40 cm。

（2） 与其它3个模型相比，Roth模型相关性最好，R2最高为0.750;且反演土壤含水量值更稳定，其中在土壤偏干旱和偏湿润条件下 RMSE 平均值分别为0.0401和0.0335 m3/m3;RE最低为3.0%。

（3） 利用探地雷达及 Dix公式对不同深度相邻反射层间土壤水分的反演具有局限性，其反演精度有待进一步加强。

参考文献：

[1] VEREECKEN H， HUISMAN J A， PACHEPSKY Y， etal. On the spatio-temporal dynamics of soil moisture atthe  field  scale[J]. Journal  of Hydrology， 2014， 516：76-96.

[2] VEREECKEN H，  SCHNEPF A， HOPMANS  J W，  etal. Modeling  soil  processes： Review，  key  challenges，and new perspectives[J]. Vadose Zone  Journal， 2016，15（5）：1-57.

[3] DE ROO R D， DU Y， ULABY F T， et al. A semi-empir‐ical backscattering model at L-band and C-band for asoybean canopy with soil moisture inversion[J]. IEEETransactions  on  Geoscience  and  Remote  Sensing，2001， 39（4）：864-72.

[4] ZRIBI M， GORRAB A， BAGHDADI N， et al. Influ‐ence  of radar  frequency  on  the  relationship  betweenbare  surface  soil  moisture  vertical  profile  and  radarbackscatter[J]. IEEE Geoscience and Remote  SensingLetters， 2014， 11（4）：848-852.

[5] PANCIERA  R，  TANASE  M  A，  LOWELL  K，  et  al.Evaluation of IEM， Dubois， and Oh radar backscattermodels using airborne L-Band SAR[J]. IEEE Transac‐tions on Geoscience and Remote Sensing， 2014， 52（8）：4966-4979.

[6] 韩东， 王鹏新， 张悦， 等.农业干旱卫星遥感监测与预测研究进展[J].智慧农业（中英文）， 2021， 3（2）：1-14.

HAN D， WANG P， ZHANG Y， et al. Progress of agri‐cultural drought monitoring and forecasting using satel‐lite remote  sensing[J]. Smart Agriculture， 2021， 3（2）：1-14.

[7] LIU X， CHEN J， CUI X， et al. Measurement of soil wa‐ter content using ground-penetrating radar： A review ofcurrent  methods[J]. International  Journal  of  DigitalEarth， 2019， 12（1）：95-118.

[8] HUISMAN J A，  SNEPVANGERS J， BOUTEN W， etal. Mapping spatial variation in surface soil water con‐tent： comparison of ground-penetrating radar and timedomain reflectometry[J]. Journal of Hydrology， 2002，269（3）：194-207.

[9] GROTE K， HUBBARD S， RUBIN Y. Field-scale esti‐mation of volumetric water content using ground-pene‐trating  radar  ground  wave  techniques[J]. Water  Re‐sources Research， 2003， 39（11）： ID 1321.

[10] GALAGEDARA L W， PARKIN G W， REDMAN J D.An  analysis  of the  ground ‐ penetrating  radar  directground wave method  for  soil water content measure‐ment[J]. Hydrological Processes， 2003， 17（18）：3615-3628.

[11] ALGEO J， VAN DAM R L， LEE S. Early ‐ Time GPR：A method  to  monitor  spatial  variations  in  soil  watercontent during irrigation in clay soils[J]. Vadose ZoneJournal， 2016， 15（11）：1-9.

[12]王前鋒， 周可法， 孙莉， 等.基于探地雷达快速测定土壤含水量试验研究[J].自然资源学报 ， 2013， 28（5）：881-888.

WANG  Q，  ZHOU  K，  SUN  L，  et  al. A study  of fast estimating  soil  water  content  by  ground  penetrating radar[J]. Journal  of Natural  Resources， 2013， 28（5）：881-888.

[13]曹棋， 宋效东， 吴华勇， 等.探地雷达地波法测定红壤区土壤水分的参数律定研究[J].土壤通报 ， 2020， 51（2）：332-342.

CAO Q， SONG X， WU H， et al. Determination of ba‐ sic parameters of soil moisture by using ground-pene‐trating radar ground wave method in red soil region of south China[J]. Chinese Journal of Soil Science， 2020， 51（2）：332-342.

[14]李蕙君， 鐘若飞.探地雷达波振幅与土壤含水量关系的数值模拟[J].应用科学学报， 2015， 33（1）：41-49.

LI H， ZHONG R. Numerical study on the relationship between amplitudes of ground penetrating radar wave and water content in soil[J]. Journal of Applied Scienc‐ es-Electronics and Information Engineering， 2015， 33（1）：41-49.

[15] CAO Q， SONG X， WU H， et al. Mapping the responseof volumetric soil water content to an intense rainfall event at the field scale using GPR[J]. Journal of Hy‐drology， 2020， 583（C）： ID 124605.

[16] CHRISTIAN H， MARIA M， ELIZABTH V， et al. Un‐derstanding  soil  and  plant  interaction  by  combining ground ‐ based  quantitative  electromagnetic  induction and  airborne  hyperspectral  data[J]. Geophysical  Re‐ search Letters， 2018， 45（15）：7571-7579.

[17] ZHOU L， YU D， WANG Z， et al. Soil water contentestimation  using  high-frequency  ground  penetrating radar[J]. Water， 2019， 11（5）： ID 1036.

[18]冉弥， 邓世坤， 陆礼训.探地雷达测量土壤含水量综述[J].工程地球物理学报， 2010， 7（4）：480-486.

RAN M， DENG  S， LU L. Review  of measuring  soil water  content  with  ground-penetrating  radar[J]. Chi‐nese  Journal  of Engineering  Geophysics， 2010， 7（4）：480-486.

[19] ANDREA B. Water content evaluation in unsaturatedsoil  using  GPR  signal  analysis  in  the  frequency  do‐ main[J]. Journal of Applied Geophysics， 2010， 71（1）：26-35.

[20] HUISMAN J A， HUBBARD S， REDMAN J D， et al.Measuring soil water content with ground penetratingradar[J]. Vadose Zone Journal， 2003， 2（4）：476-491.

[21] KATERINA Z， TOMAS C. Application of ground pen‐etrating  radar  methods  in  soil  studies： A  review[J].Geoderma， 2019， 343：116-129.

[22] ELIA S， ANTONIO B， PIETRO T， et al. Simultaneousmonitoring  of soil  water  content  and  salinity  with  alow-cost  capacitance-resistance  probe[J].  Sensors，2012， 12（12）：17588-17607.

[23] TOPP G C， DAVIS J L， ANNAN A P. Electromagneticdetermination of soil water content： Measurements incoaxial  transmission  lines[J]. Water  Resources  Re‐search， 1980， 16（3）：574-582.

[24] ROTH C H， MALICKI M A， PLAGGE R. Empiricalevaluation  of the  relationship  between  soil  dielectricconstant and volumetric water content as the basis forcalibrating  soil  moisture  measurements  by  TDR[J].Journal of Soil Science， 1992， 43（1）：1-13.

[25] HERKELRATH W N， HAMBURG S P， MURPHY F.Automatic real‐time monitoring of soil moisture in a re ‐mote field area with time domain reflectometry[J]. Wa‐ter Resources Research， 1991， 27（5）：857-864.

[26] FERRE P A， RUDOLPH D L， KACHANOSKI R G.Spatial averaging of water content by time domain re‐flectometry： Implications for twin rod probes with andwithout  dielectric  coatings[J]. Water  Resources  Re‐search， 1996， 32（2）：271-279.

[27] GREAVES，  LESMES  R  J，  LEE  D  P，  et  al. Velocityvariations and water content estimated from multi-off‐set ground-penetrating radar[J]. Geophysics， 1996， 61：683-695.

[28] OVERMEEREN R A， SARIOWAN S V， GEHRELS JC. Ground penetrating radar for determining volumet‐ric soil water content; results of comparative measure‐ments at two test sites[J]. Journal of Hydrology， 1997，197（1）：316-338.

[29] DIX  C  H. Seismic  velocities  from  surface  measure‐ments[J]. Geophysicists， 1955， 20（1）：68-86.

[30] HUISMAN J A， SPERL C， BOUTEN W， et al. Soil wa‐ter content measurements at different scales： Accuracyof time  domain  reflectometry  and  ground-penetratingradar[J]. Journal of Hydrology， 2001， 245（1）：48-58.

Monitoring Specified Depth Soil Moisture in Field Scale with Ground Penetrating Radar

ZHANG Wenhan1 ， DU Keming2* ， SUN Yankun1* ， LIU Buchun2 ， SUN Zhongfu2 ， MA Juncheng2 ， ZHENG Feixiang2

（1. College of Resources and Environment， Northeast Agricultural University， Harbin 150030;2. Institute of Envi‐ronment and Sustainable Development in Agriculture， Chinese Academy of Agricultural Sciences， Beijing 100081）

Abstract： Ground-penetrating radar （GPR） is one of the emerging technologies for soil moisture measurement. However， the measurement accuracy is difficult to determine due to some influence factors including radar wave frequency， soil texture type， etc. The GPR equipment with 1000 MHz center frequency and the measurement method of common midpoint （CMP） were ad‐ opted in the research to collect radar wave raw data in the selected field area under arid soil and moist soil conditions. The trans‐mitter and receiver antennas of the GPR equipment were moved 0.01 m respectively in opposite directions on each radar wave raw data collection. Therefore， a CMP radar image consisted of 100 pieces of radar wave raw data by increasing the antenna dis‐tance from 0 m to 2 m. Each radar wave raw data indicated that the radar waves were reflected in the reflective layer with differ‐ent dielectric constant under the same antenna distance. And the reflected and refracted radar waves were acquired by the receiv‐ing antenna at different two-way travel time respectively， and recorded in the computer. The collection of CMP soundings aimed to determine the inversion accuracy， optimum inversion depth， effective inversion depth and optimal inversion model of soil moisture content at different depth ranges and adjacent reflective layers by GPR at field scale. The reflected and refracted radar wave data were extracted from the raw data. The velocities of the surface waves and reflected waves were obtained respectively from the line slope of the surface wave data and the hyperbolic curves fitting of the reflected wave data. In addition， the relative dielectric constant of the soil at specified depth were deduced according to the soil dielectric constant and its reflected wave ve‐locity. Moreover， 4 different models including Topp， Roth， Herkelrath and Ferre were used to figure out the soil volumetric wa‐ter content inversion. Meanwhile， the measured data of soil volumetric moisture content obtained by oven drying method were used to verify the accuracy of the inversion results. The results showed that the effective inversion depth of 1000 MHz GPR ranged from 0 to 50 cm. The best inversion depth was 50 cm in arid soil and 40 cm in moist soil. The Roth model had the best correlation and stability with the highest R2 was 0.750， the Root Mean Square Error （RMSE） was 0.0114 m3/m3 and the lowest Relative Error （RE） was 3.0%. The GPR could possess the capacity of quick， precise and non-destructive measurement of speci‐fied depth soil moisture in field scale. The inversion model of soil moisture content needs to be calibrated according to different soil conditions.

Key words： ground penetrating radar; soil water content monitoring; common midpoint; optimum inversion depth; optimum in‐ version model; Roth model