物理课堂中的迁移式情境教学
封玉林

新高考改革在上海已经实行多年,伴随着制度的变革,考试内容和形式的改变是教师和学生关注的重中之重。对物理学科而言,不难发现一个事实:新的选考模式相对于原先的考试难度降低了,而对物理学基本核心素养的要求更高了。尤其在物理观念的建立、科学思维的提升、实验探究以及科学态度等能力方面提出了更高的要求。伴随着命题者如何考查学生各项素养并体现出区分度的思考,情境化的出题模式便随着考改应运而生。针对这种情况,高中物理教学过程中应适度地加入情境教学模式,通过一些学生头脑中已有的常识作为切入点,为学生营造更加丰富有趣的情境,激发学生学习兴趣,最终加深对概念的理解和运用能力。
一、情境式教学的三个步骤
物理教学应该是从情境中来,再到情境中去。创设情境其实只不过是情境教学的一个起始环节,完整的情境教学至少应该包括三部分,即情境化、去情境化与再情境化物理教学。既要让学生从纷繁复杂的现象中发现普遍规律并建立起揭示其本质特征的物理概念,实现从情境到概念的理论构建——即从“情境化”到“去情境化”的过程,又要能将概念还原到现实情境中用于解决实际问题,实现从概念到应用的经验还原——即从“去情境化”到“再情境化”的过程。
(一)情境化:产生问题
中学生的认知发展水平处于形象思维和抽象思维的过渡阶段,处于这一阶段的学生,能够理解并解决简单的抽象问题,但对于从未接触过的概念仍需要一定的感性认知來支撑,在教学中需要“情境”的支撑,来使学生获得关于未知内容的感性认识。感性认识是发展理性认识的基础,良好的教学情境则可以给学生提供感性的认知经验,为知识的建构做好准备。从学习心理角度看,有趣的情境能调动学生的学习兴趣,促进学习活动的持续进行;从学习经验角度看,熟悉的情境为学生提供了感性认识的基础,促进了概念形成;从学习发展角度看,情境的变化能带动知识的迁移,发展学生的思维,引出核心问题。而从教师的教学来看,如何在建立概念、引导学生由感性思维到抽象思维的过程中,创设“情境”以及由“情境”设计出怎样的“问题”成为最关键的环节(或者说,提问永远是课堂的艺术所在)。如在讲解产生滑动摩擦力的条件时,可现场演示将粉笔擦沿着竖直黑板面自由下落,此过程中虽然板擦与黑板接触但由于没有相互之间的弹力,所以就不会将黑板上的字擦除,由此引出产生摩擦力的条件。
(二)去情境化:分析问题
“去情境化”重视从感性认识到理性认识的飞跃,通过具体情境帮助学生形成形象的思维和感性的认识,但对于这些繁复的知识仅靠学生自己在情境中建构是远远不够的。教学的主要任务是帮助学生筑起知识的大厦,使其获得大量抽象概括的一般化知识和思维方法,形成知识体系。所以在情境教学中我们既要为学生呈现一定的具体情境,又要帮助他们脱离情境,建构一般化的知识。这就需要教师进行情境教学中的第二个环节——“去情境化”。“去情境化”是指将知识从具体的情境中分离抽象出来,从而超越情境,成为概括性的知识,是情境教学中重要的一环。
(三)再情境化:重现问题
再情境化实际上就是通过概念与迁移情境相结合,进一步对概念进行辨析和应用,对概念雏形中的细节进行调整,最终形成科学而系统的解决方案,并对概念的本质特征和思维方式进行巩固和应用。学生解决问题的能力是知识应用能力的更高进阶,在本质上可以看成是一种学习迁移能力。创设这些条件性情境的目的,也是希望使学生的学习内容情境化,或者期望学生将知识迁移到新的情境中,更好地解决新情境下的问题。情境教学中的“再情境化”就凸显出了其促进学习迁移的重要意义。
二、情境式教学案例
情境下的考题也就是“信息题”,是指通过将考生所掌握的公式、原理、结论、生活中的场景、最新科技成果等以已知的信息渗透在某一物理问题中,要求考生临场自主阅读、独立提取题目中的信息、结合头脑中的原有知识进行模型构建,在全新的情境中将学过的知识即时应用于真实问题解决中的试题。其优点:情境新,阅读量大,贴近生活。由于信息题的“信息”具有新颖性,要求考生在考场上即时自主阅读,领会信息的含义,即时结合原有知识构建物理模型。而在平时训练中,学生接触到此类情境题,往往凭主观感觉,很容易割裂理论和情境,造成此类问题大量失分。这就意味着教师更需要去引导学生学会超越情境,还原本质,形成概括化知识,最终实现迁移,即为“去情境化—再情境化”的习题教学模式。
(一)结合案例,提出问题
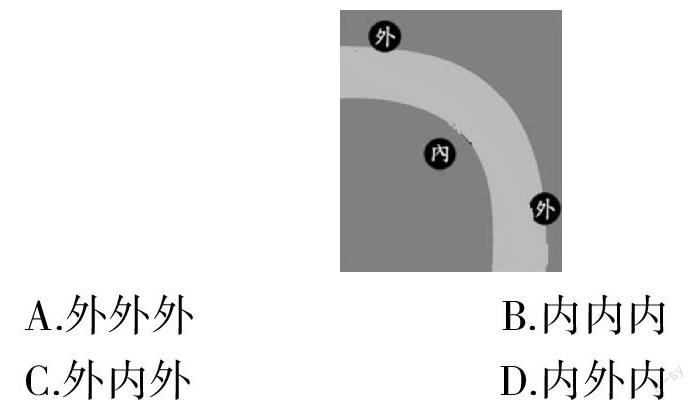
情境:如图是F1方程式赛车比赛中“上”赛道的一个直角弯角,赛车手驾驶赛车从图片右下角进入视线,图中标出的是赛道的内外两侧,请问在过弯不减速的情况下,他应该选择的最合理的过弯路线是( )
对于此类问题学生普遍按照直觉去处理问题,而非找到理论去解释现象,为此笔者设计以下问题去引导学生的思维:
1.转弯过程中,赛车在水平方向受到几个力?找到水平方向的外力并作出受力分析图。
2.请根据匀速圆周运动特点,思考合力的作用是什么?如何选择物理公式求出转弯速度和转弯半径的关系?
3.赛车是一项追求极限速度的项目,在最大静摩擦力一定的情况下,谈谈如何理解最佳过弯的路线。
在这三个问题的引导下,将赛车转弯这一情境抽离出题目,将它变成在水平方向作匀速圆周运动的力学问题。在剥离复杂情境后,便于学生搭建最基本的力学模型,为接下来的去情境化的登场做好铺垫。
(二)抽丝剥茧,还原本质
学生在对情境有了一定的分析之后,教师适时给出学生熟悉的模型进行类比。
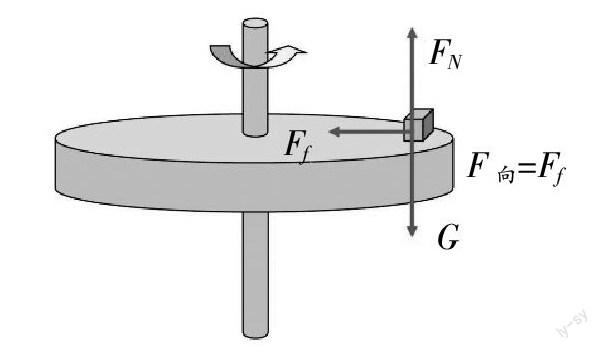
模型:一个圆盘在水平面内匀速转动,盘面上有一个物体相对转盘静止,随盘一起做匀速圆周运动,物体与圆盘之间的最大静摩擦力为Ff,试分析物体在距圆盘中心不同位置处的最大线速度。
学生在与之前的模型对比之后,发现抽象过的赛车模型与圆盘模型同出一辙,静摩擦力提供向心力,根据F向=m■可知,在向心力一定的情况下,半径越大,对应的线速度也越大。所以在赛车问题中,在最大静摩擦力一定的情况下,为获得最大的过弯速度,应选择最大转弯半径的路径,即外内外这一路径。从特殊到一般的思路,摒弃特殊情境带来的干扰,找到共性,真正实现知识的迁移和灵活应用。
(三)情境回归,获得新知
与“情境化”类似,“再情境化”同样是通过创设情境来帮助学生学习,但此时情境的创设却又区别于“情境化”,此时情境创设的目的是发展学生更高阶的解决问题的能力,期望学生将知识迁移到新的情境中,通过新情境的迁移螺旋式提升学生解决实际的能力。
情景回归1:在高速公路的拐弯处,为什么将路面设计成外高内低?
情境回归2:如图所示,在某路段汽车向左拐弯,司机左侧的路面比右侧的路面低一些。汽车的运动可看作是做半径为R的圆周运动。设内外路面高度差为h,路基的水平宽度为d,路面的宽度为L,已知重力加速度为g,要使车轮与路面之间的横向摩擦力(即垂直于前进方向)等于零,则汽车转弯时的车速应等于多少?
情境回归3:如图所示,火车道转弯处的半径为r,火车质量为m,两铁轨的高度差为h(外轨略高于内轨),两轨间距为L(L>>h),求:火车以多大的速率v转弯时,两铁轨不会给车轮沿转弯半径方向的侧压力?
以上三个问题是一种递进的关系,在掌握圆盘模型的基础上,从第一个问题出来做出定性分析到第二个问题的定量计算,直到第三个问题的定量讨论。多次体验了与情境模型的深度匹配,并不断进行决策的优化——这既是一个倒推验证的过程,更是一个体系生成的过程。
三、小结
在突出以学生为主体的高中物理教學课堂的背景下,情境式教学已经逐渐显现出其优势,不仅符合学生的思维习惯,能充分调动学生学习积极性,也符合新课标对于高中物理教学的要求,并在教学实践中发挥着积极有效的作用。如何在日常教学中结合学生已有的知识经验,引导学生更多地从理性思维角度而非感性直觉角度去思考问题,如何营造一种和谐的教学氛围,不断丰富教学方法、教学情境,通过问题情境教学培养学生自主学习的能力,最终促进物理课堂教学质量的提高,这对于教师也提出了更高的要求。
参考文献:
[1]胡志强.浅析高中物理教学中问题情境的创设[J].中国校外教育,2019(17):96.
[2]梁沛林.从物理核心素养培养谈物理课堂情景化实验引入[J].物理通报,2020(2):36.
[3]赵航.基于情境化、去情境化、再情境化探究式案例教学模式研究[J].管理案例研究与评论,2015(6):30.

