有趣的角
刘彭旖


我喜欢数学,更喜欢思考!前几天学习“画角”时,我遇到了这样一道数学题:用一副三角尺画一个15°的角。“这很简单呀!”我心想,“三角尺上的角有90°,45°,30°和60°,把45°角和30°角重叠摆放,就可以得到15°角了。”
我赶忙拿出三角尺摆弄起来,很快完成了这道题目(如图1)。突然,我的脑袋瓜里蹦出了一个问题:除了三角尺上原有的角和15°角,用一副三角尺还能不能画出其他的角呢?
在好奇心的驱使下,我又用这副三角尺拼摆了起来。在不断的尝试中,我发现:
30°和45°拼在一起可以形成75°;
60°和45°拼在一起可以形成105°;
30°和90°拼在一起可以形成120°;
45°和90°拼在一起可以形成135°;
60°和90°拼在一起可以形成150°;
90°和90°拼在一起可以形成180°。
看着这些新拼出来的角,我高兴极了!接着一个新的问题随即冒了出来:一副三角尺到底能拼(画)出哪些角呢?我将这些角按照从小到大的顺序排了出来:15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,180°。“噢——原来如此!”我忍不住叫出声来,“它们都是15°的倍数!”正当我得意扬扬时,却发现150°和180°之间少了个165°。没错!如果我的发现成立,165°角应该也能画出来。于是,我再次拿起三角尺研究起来。可我用一副三角尺不管怎么拼都沒能成功!“难道165°真是个例外?”我心里想着,再次陷入沉思。这些角里,有的是三角尺上包含的一个角,有的是用三角尺上的两个角拼出来的……既然可以用两个角拼,那就可以用三个角拼,我又找来一个含30°角的三角尺。对了!165°=90°+45°+30°。这是一个重大发现,我迫不及待地去和爸爸分享。爸爸听了我的分享,高兴地竖起了大拇指,说:“你真是一个善于思考的孩子!那爸爸再考考你,可不可以用一个含有30°角的三角尺画出一个15°的角呢?”
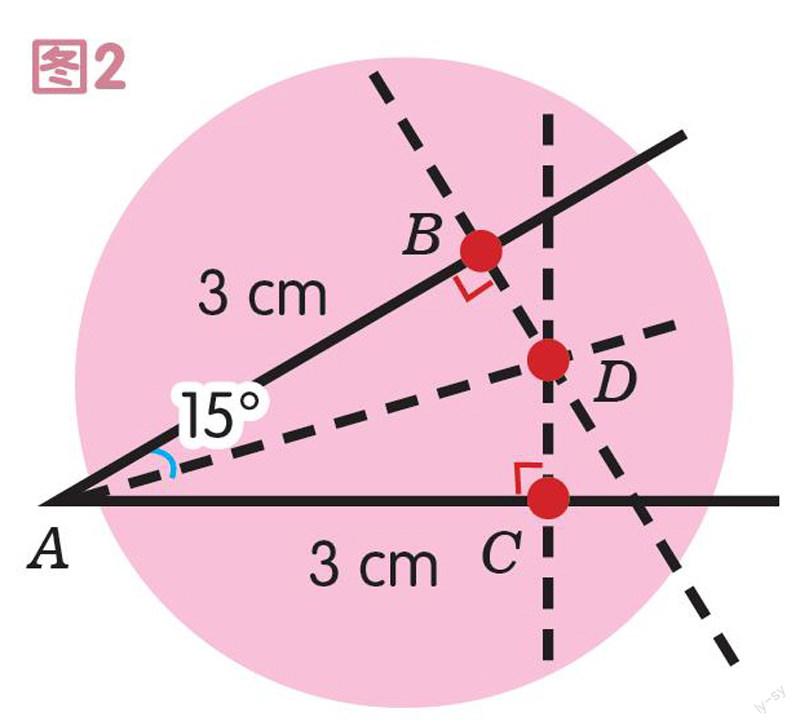
我刚开始觉得这根本就不可能,但是爸爸却让我认真地想一想。于是,我就认真地思考了很久,终于想出了一个办法(如图2)。
首先从30°角的顶点A开始,在两边距离A点3 cm处画上标记B和C。然后过B点和C点各画一条与AB、AC分别垂直的直线,两条垂线相交于点D。最后,连接AD,这个30°的角就被平均分成了两个15°的角。
可是,为什么会这样呢?
我又仔细地观察了我画的图形,惊喜地发现:△ABD和△ACD都是直角三角形,而且它们有两条边的长度是一样的,AB=AC,又共用了同一条边AD。所以△ABD和△ACD的大小、形状完全一样,那么就有∠BAD=∠CAD,也就是直线AD平分∠BAC啦。当我把我的想法告诉爸爸时,爸爸激动地说:“太棒了,这是到了中学才会学到的知识!”
“数学真是太有趣了!”我高兴地跳了起来。简简单单的一副三角尺就可以画出这么多有规律的角!我心想:用这种方法,是不是还可以画出7.5°角呢?同学们,你们知道怎么画吗?赶快动手试一试吧!
指导老师 白翠霞
个人档
710061 陕西省西安市
陕西师范大学附属小学四(10)班
李婉悠 10月6日 16:03:12
我参考彭旖的方法,先画出含有15°角的直角三角形ACD,再以点A为定点,在距离A点2 cm处分别做标记E、F。过点E和点F分别作AC、AD的垂线,两条垂线相交于点G,连接AG后就得到两个7.5°的角了。
豆悦熙 10月6日 17:25:13
彭旖的方法是一个证明三角形全等的定理:如果两个直角三角形的斜边及一条直角边对应相等,那这两个三角形全等。需要注意的是,这种方法只能用于直角三角形,其他的三角形都不适用哟!
谢雨珂 10月6日 19:03:20
受到彭旖的启发,我也想了一道新题目:△ABC中,D是BC的中点,DE=DF。大家能证明AB=AC吗?

