数值计算软件建模在篮球教学中的应用

杨杰　柏杨　杨倩玉　王闻婕　钱嘉斌

关键词： 建模;数值计算软件;篮球;教学

中图分类号： G 642.00 文献标志码： A 文章编号： 1009?895X（2022）02?0185?05

DOI：10.13256/j.cnki.jusst.sse.2022.02.013

篮球运动自1891 年发明以来，深受广大人民群众的喜爱。无论是在国际赛事，还是在小学、中学、大学的体育课堂，篮球都占据着重要地位。众所周知，篮球以投篮进球作为得分的手段和判据，那么如何通过训练来提高投篮命中率便成为教练员和篮球运动员一直追求的目标。为了达到这一目标，许多学者针对篮球的教学与训练、投篮命中率的提高等方面进行了系统的研究。

在篮球的教学与训练方面，学者们首先对目前篮球教学与训练中存在的问题进行了介绍。其中，胡锴[1] 介绍了篮球教学的训练方式中存在的问题主要为训练方式传统化和忽视学生之间的个体差异;朱金阁[2] 介绍了现阶段中高等院校篮球教学与训练中存在的最大问题为教学资源的匮乏;钱博文[3] 介绍了高校篮球教学存在的问题主要包括对篮球运动的认识存在偏差、学生篮球水平参差不齐、考核和评价体系建设滞后等方面。而后，针对所存在的问题展开了详细的分析，并分别针对篮球训练方式的完善和教学方法的改革给出了合理化建议与解决方法。针对篮球训练方式的完善，可通过游戏训练法[1]、拓展训练法[4] 和意识训练法[5] 的运用激发学生学习兴趣、提高训练效果。针对篮球教学方法的改革，可通过改进教学方法[6] 和创新教学方式[7] 进行课程创新，从而为高校篮球的可持续发展提供动力。

在投篮命中率的提高方面，根据采用方法、手段或技术的不同，学者们分别基于各研究方法、高科技手段和学科交叉技术对其进行了研究。其中，基于各研究方法，张堃[8] 通过文献资料法、数理统计法和队员访谈法对朝阳市天天篮球俱乐部队员中距离投篮命中率的影响因素进行了分析;甘磊军[9]采用调查问卷法、访谈法、文献资料法和数理统计法，从多个角度、不同层次分析了篮球运动中影响投篮命中率的因素;袁泓[10] 通过理论分析法、文献资料法和观察比較法等方法，研究了篮球投篮技术动作与投篮命中率之间的关系;罗莉[11] 运用文献资料法、实验法、调查问卷法、对照分析法等方法，对篮球教学过程中如何快速提高投篮命中率进行了研究。基于高科技手段，师珂[12] 通过高速摄像机拍摄的方式研究了罚球线、罚球圈和三分线处原地单手肩上投篮命中率最高的出手角度或出手角度区间，并探明了影响出手角度的客观因素。基于学科交叉技术，杨杨[13] 利用Mimics 和Ansys 软件提出了一种基于有限元的篮球运动员投篮目标技术优化培训方法;赵海鹤[14] 运用力学原理研究了篮球训练中提高投篮命中率的方法。

通过以上的研究可以发现，篮球的教学与训练及投篮命中率受到教练员、运动员、日常训练、比赛场地、比赛时间、心理素质等多个因素的影响，这为教练员的指导与篮球运动员的训练增加了难度。在此背景下，能否提供一种可视化、可量化的篮球运动轨迹模拟，为教练员和篮球运动员提供清晰、便捷、准确的投篮路线判断，并在此基础上进行训练是极具意义的。

鉴于此，本文采用能源动力类数值计算软件对不同情况下的投篮过程进行建模，对实际投篮过程进行运动轨迹模拟，探索篮球运动规律，分析提高投篮命中率的方法。从而为教练员的指导提供可量化的科学支持，为篮球运动员提高投篮命中率提供可视化的科学依据，快速提高训练效率。

一、有限元分析

（一）篮球模型的建立

采用能源动力类数值计算软件ABAQUS 对篮球进行建模。其中篮球直径为246 mm，重力加速度为9800 mm/s²，网格单元类型采用线性减缩积分单元CPE4R。篮球模型网格划分如图1 所示，本模型共包括348 个节点，311个单元。

（二）投篮过程的有限元建模

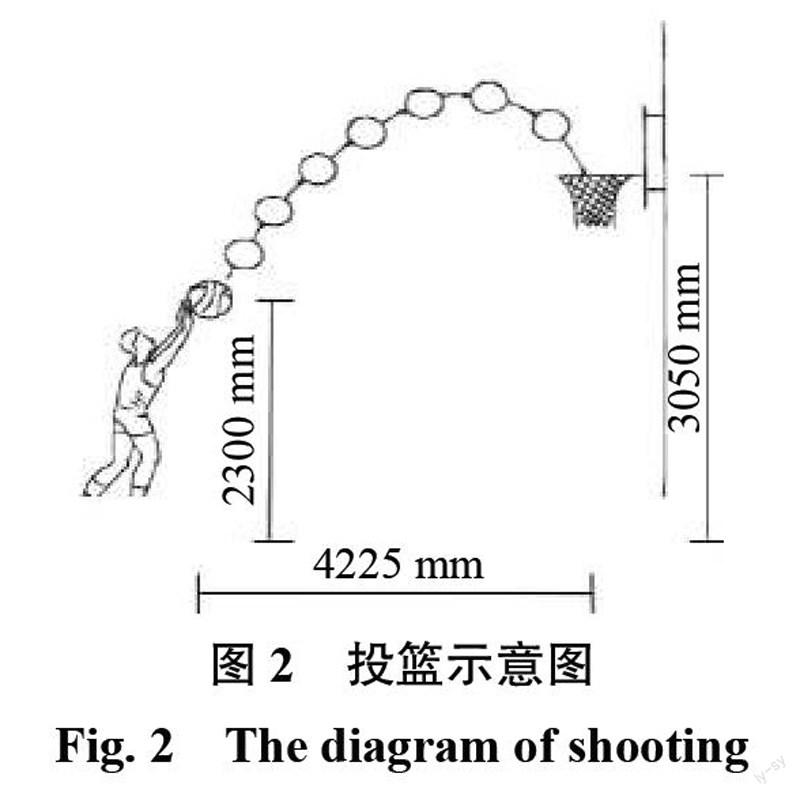
假设篮球运动员身高1 800 mm，跳投时脚离开地面高度100 mm，投篮时手臂高过头顶400 mm，即出手点距离地面2 300 mm。投篮位置为罚球线附近，出手位置距离篮筐4225 mm，篮筐高3 050 mm。以出手点为坐标原点（0mm， 0mm），则目标点坐标为（4225 mm，750 mm），如图2 所示。

投篮过程的模拟通过两个分析步实现。在第一个分析步中，对篮球左下角45°位置施加沿X 方向与沿Y 方向的位移，将篮球“投到”一定的高度和远度，并施加重力载荷。在第二个分析步中，仅对篮球施加重力载荷，使篮球进行自由落体运动。两个分析步的加载情况如图3 所示。

通过改变沿X 方向位移和沿Y 方向位移的大小，改变不同的出手角度，并使篮球达到不同的高度和远度，模拟不同情况下的投篮过程。

二、结果与讨论

（一）不同投篮高度对篮球运动轨迹的影响

在第一个分析步中，固定篮球沿X 方向的位移为2450mm，依次改变篮球沿Y 方向的位移，使合位移与X 方向的夹角即出手角度依次为20°，25°，30°，35°，40°，45°，50°，55°，60°，65°。从而将篮球投到相同的远处、不同的高度，以研究不同投篮高度对篮球运动轨迹的影响。不同投篮高度下篮球的运动轨迹如图4 所示。

从图4 中可以观察到，投篮高度与出手角度呈正相关，随着投篮高度和出手角度的增加，篮球运动轨迹间的差异也逐渐增加。篮球在下降段变得更加陡峭，即投进篮筐的入射角更大，更加容易进球。

此外，由于惯性的原因，在第一个分析步结束后篮球继续向前运动一段距离，且这段距离随着投篮高度的增加而增加，这才出现了各条曲线中最高点的X 坐标随着投篮高度的增加而逐渐增加的现象。

（二）不同投篮远度对篮球运动轨迹的影响

在第一个分析步中，固定篮球沿Y 方向的位移为2 056 mm，改变篮球沿X 方向的位移，即将篮球投到相同的高度、不同的远度，以研究不同投篮远度对篮球运动轨迹的影响。与节3.1 一样，这些投篮远度也是按照不同的出手角度来设置的，随着投篮远度的增加，所对应的与X 方向的出手角度依次为65°， 60°， 55°， 50°， 45°， 40°， 35°， 30°，25°，20°。不同投篮远度下篮球的运动轨迹如图5所示。需要说明的是，图5 中出手角度视觉上的差异是由于X 轴与Y 轴坐标差异过大所造成的。

从图5 中可以观察到，投篮远度与出手角度呈负相关，随着投篮远度的减小和出手角度的增加，篮球在空中的飞行距离降低，这清晰地展现了平时所说的“见高不见远”的情境。此外，随着投篮远度的增加和出手角度的减小，篮球运动轨迹间的差异逐渐增加，篮球在下降段变得平缓，不利于其投入篮筐。

（ 三）不同出手角度下均能得分的篮球运动轨迹

在篮球运动中，投篮得分是最终目的。为此，在出手角度分别为20°，25°，30°，35°，40°，45°，50°，55°，60°，65°时，同时调整篮球沿X 方向和沿Y 方向的位移，得到在不同出手角度下均能投篮得分的篮球的运动轨迹，如图6所示。

从图6 中可以清晰观察到，随着出手角度的逐渐增加，要想投篮得分，需要逐渐增加投篮高度、降低投篮远度，反之亦然。随着出手角度的减小，篮球进入篮筐的入射角降低，对入框不利。这也说明了投的很平（出手角度很小）的球很难得分的原理。

文献[12] 中指出，最佳的入篮角度为38°-45°，根据图6 的结果，测得最佳的出手角度为50°-55°，这与文献中根据实验得到的罚球线处命中率最高的出手角度为52°-54°是吻合的[12]。

此外，将第一个分析步中对篮球施加的沿X 方向与沿Y 方向的位移进行合成，以二者的合位移来定性表达对篮球所施加的力的大小。不同出手角度下对篮球施加的合位移如图7 所示。

从图7中可以发现，随着出手角度的增加，投篮得分所需要的力呈现先降低再增加的趋势。当出手角度为30°时，投篮所需提供的力最小。对比篮球最佳出手角度50°-55°可以得到，对篮球运动员进行一定的核心力量训练是必要的，有助于提高出手角度和投篮命中率[15]。

（四）投篮得分曲线及其数学表达式

为研究投篮得分的规律，将节3.3中所设置的不同出手角度下均能得分的沿X 方向和沿Y 方向的位移汇总如图8 所示。可以发现在投篮得分时，籃球沿X 方向的位移（即投篮远度）和沿Y 方向的位移（即投篮高度）呈指数函数关系，如式（1）所示：

此指数函数即为投篮得分曲线的数学表达式。该条曲线可以为教练的指导与篮球运动员的训练提供参考。

需要说明的是，每个篮球运动员因身高、臂展、跳投高度、投篮习惯等因素的不同，所拥有的投篮运动轨迹和投篮得分曲线是不同的。在篮球实践中，可以首先通过测量法和数理统计法得到每一位篮球运动员的身高、臂展、跳投高度、出手点位置和出手角度等基本数据，然后根据这些基本数据调整本模型中的参数，从而得到每一位篮球运动员的投篮运动轨迹和投篮得分曲线。根据所得到的投篮运动轨迹和投篮得分曲线，反过来对篮球运动员的投篮进行调整。

本方法可以为教练员在经验指导的基础上提供可量化的科学支持，为篮球运动员在日常训练的基础上提供可视化的科学依据，从而有助于提高训练效率、提高投篮命中率。

三、结论