深度教学“U型”模式的实践

实施深度教学,有利于培养学生的核心素养,发展深度教学是符合核心素养要求的,导向深度教学的有效模式是“U型”模式。“U型”模式的教学设计能引发学生高阶思维、丰富学习经历,使数学学习真实发生、深度发生,有利于教学目标的完整达成和深度达成。
一、深度教学“U型”模式的内涵
深度教学“U型”模式是华中师范大学郭元祥教授对美国教育家杜威的经验教学过程理论的总结概括。杜威认为纯粹的符号知识具有不可教性的特点,要把书本知识变成个人知识必须经历还原—理解—探究—体验—反思的学习过程。即知识的理解与学习需要经过下沉、潜行、上浮的“U型”过程。首先,是知识还原的“下沉”环节,即建立书本知识与学生个人经验的关联,对知识进行表征化、具象化的过程。其次,是对知识进行自我加工的“潜行”环节,即引导学生深度理解、体验、对话、探究知识的过程。最后,是进行反思性思维的“上浮”环节,即反思性思维过程。反思与上浮在整个“U型”中最重要,是指学生在深度探究知识后及时展开反思,将经过“自我加工”书本知识进行个人意义的升华和表达,书本知识才能真正变成个人知识。
二、基于深度教学“U型”模式的活动设计
(一)下沉:知识的还原
1.创设情景,导入新课
同学们,你们想去逛商场吗?(想)现在我们就去商场逛逛吧(播放双11促销活动视频)。大家看到了什么?“双11巨惠,全场5折优惠”“双11优惠大酬宾,全场商品一律折上折销售”“相约双11,买1送1”……商家会亏本打折吗?灵活地运用打折促销艺术是商家成功的秘诀之一,本节课我们共同来探索打折促销的奥秘。
设计意图:通过双11促销活动视频创设打折销售情景,使学生置身于真实的环境中,产生用数学知识解决实际问题的强烈愿望,为学好本节课奠定了坚实的情感基础。
2.欣赏小品,理解概念
由四名同学表演小品《卖铅笔》。
批发商:在桌子上摆放各种商品,旁边立广告牌:本店只做批发,不零售。铅笔5元/盒,规格:10支/盒;签字笔……
小商贩:我批发一盒铅笔,(付5元钱,他拿回去后,在教室里来回走动,进行零售)卖铅笔了,跳楼价,1元一支,多买优惠。
顾客A:老板,你这铅笔咋卖呀?
小商贩:1元1支,多买优惠。
顾客A:那我要2支呢?
小商贩:2支太少,不优惠。
顾客A:那好吧,给我来2支。(付2元钱离开)
小商贩:(继续叫卖)卖铅笔了,跳楼价,1元1支,多买优惠。
顾客B:老板,你这铅笔多少钱1支?
小商贩:1元1支,多买优惠。
顾客B:剩下的我全要了呢?
小商贩:给你打9折吧。
顾客B:9折(停顿),太贵了,6折怎么样?
小商贩:6折不行,就亏本了,给你打7折。
顾客B:(付5.6元钱离开)
小商贩:最后把手中的钱点了一下,自言自语地说:“今天我赚了2.6元。”
设计意图:通过学生扮演批发商、小商贩和顾客A、B模拟商品买卖中讨价还价的情景,增强课堂画面感,使抽象的知识具象化,便于理解成本价、标价、销售价、折扣、利润等概念及它们之间的关系,为学好本节课奠定了坚实的知识基础。
(二)潛行:自主探究,建构模型;合作体验,巩固提升
1.自主探究,建构概念
问题1:小商贩购进的铅笔每支成本价是多少?
预设生成:成本价每支0.5元。
问题2:小商贩销售铅笔时的标价是多少?他是在成本价的基础上提高多少元标价的,提高的百分率是多少?
预设生成:标价每支1元;提高0.5元标价,提高的百分率是100%。
问题3:对顾客A的销售价是多少?每支铅笔盈利多少?每支铅笔利润率多少?
预设生成:销售价每支1元;每支盈利0.5元;每支利润率100%。
问题4:对顾客B打几折销售的?销售价是多少?每支铅笔盈利多少?每支铅笔利润率多少?
预设生成:打7折销售;销售价每支0.7元;每支盈利0.2元;每支利润率40%。
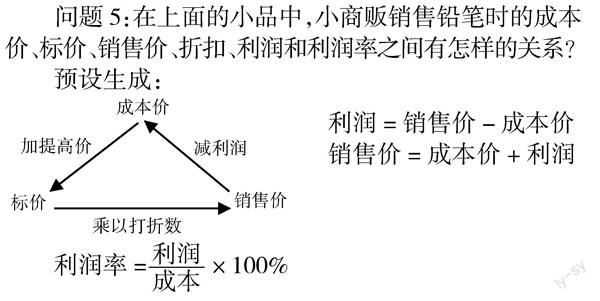
问题5:在上面的小品中,小商贩销售铅笔时的成本价、标价、销售价、折扣、利润和利润率之间有怎样的关系?
预设生成:
[成本价][加提高价][减利润][乘以打折数][标价][销售价] [利润=销售价-成本价
销售价=成本价+利润]
利润率=×100%
销售价=成本价×(1+利润率)
设计意图:通过亲身体验、自主探究,辨析成本价、标价、销售价、折扣、利润、利润率等概念,理解并掌握它们之间的关系,为利用方程模型解决实际问题做好知识储备。
2.典例探究,建构模型
例1:甲同学批发了一种签字笔,按进价提高50%标价,再打8折销售,每支仍可盈利0.4元,这种签字笔的进货价是多少元?
问题6:这0.4元的利润是怎么来的?
预设生成:利润=销售价-进货价
问题7:如果设这种签字笔每支的进货价为x元,那么标价为多少元?销售价为多少元?利润为多少元?你能列出方程解决这个问题吗?
预设生成:标价:(1+50%)x元;销售价:(1+50%)x×80%元;利润:[(1+50%)x×80%-x]元。
(1+50%)x×80%-x=0.4
解,得x=2。
答:这种签字笔每支的进货价是2元
设计意图:问题6通过提问“这0.4元的利润是怎么来的”引发学生深度思考;问题7当学生不能独立完成时,使学生在问题串的启发下获得解题经验。使不同的学生在数学课上得到不同的发展,为每一个学生提供多样性的发展空间。
例2:乙同学批发了一种橡皮,每块的进价5元,标价8元,为了薄利多销,准备打折销售,要使利润率为20%,这种橡皮应该打几折销售?
问题8:本题涉及打折销售中的哪些量?利润率如何计算?
预设生成:进价、标价、折扣、利潤率;利润率=×100%
问题9:怎样设未知数?你能列出方程解决这个问题吗?
预设生成:设应打x折销售,则
×100%=20%
解,得x=7.5
答:这种橡皮应该打7.5折
设计意图:问题8引导学生分析题中涉及的量以及利润率的计算方法,为进一步利用方程模型解决问题奠定基础;问题9由于学生已具备相应的基础知识,用一元一次方程解决问题便水到渠成,进一步体会方程的模型思想和数学的应用价值,提升分析、解决问题的能力。
3.合作体验,巩固提升
(1)变式训练
问题10:新华书店将一种进价22元的新书按标价的8折出售,仍可获利20%,问这种新书标价多少元?
设计意图:实现对“教”与“学”的及时反馈和纠正,使教学目标深度达成。
(2)挑战自己
问题11:尝试创编打折销售问题,并用方程思想解答。(邻桌的同学两人一组互相批改)
设计意图:考查学生灵活运用打折销售中几个量之间的关系提出问题和解决问题的能力,进一步培养学生的高阶思维能力。
(3)角色转换
问题12:两家商店销售同一品牌商品,A商店销售价为每件60元,不还价;B商店标价为每件110元,但 “让利顾客,6折酬宾”。
①如果你是消费者,你会去哪家商店消费?
②如果你是商店老板,你会使用哪种营销方式?
设计意图:通过角色转换,对同一个问题,能否从不同的角度给出合理的解释,培养思维的深刻性。
(4)链接中考
(2021,陕西)一家商店在销售某种服装(每件的标价相同)时,按这种服装每件标价的8折销售10件的销售额,与按这种服装每件标价降低30元销售11件的销售额相等.求这种服装每件的标价?
设计意图:让学生提前了解一下中考对这部分知识的要求,感受一下中考题现在我们就能解决,激发学生的求知欲。
4.分层作业
(1)基础题
①李超按原价的6折买了一个篮球,比按原价购买节省了50元,这种篮球的实际售价是多少元?
②一件商品标价121元,若以7折销售,仍可获利10%,这件商品的进价是多少元?
(2)能力题
①秀丽服装店两件进价不同的衬衫都以135元售出,A衬衫是按成本价提高50%标价,然后再打8折销售,B衬衫是按成本价提高80%标价,然后再打5折销售。秀丽服装店卖这两件衬衫总体上是赔了还是赚了?
②某品牌手机,若按标价打8折销售,一部可获利600元,其利润率20%,如果按同一标价打9折销售该手机一部,可获利润多少元?
(3)素养题
以“生活中的数学——打折销售”为题,写一篇小论文。
设计意图:面向全体学生,设计分层作业,满足不同层次学生的需求,使不同层次的学生在数学上得到不同的发展。
(三)上浮:总结反思,内化提升
通过本节课学习,你有什么收获?今后再去商场消费,你能否理智面对各种打折促销活动?
设计意图:学生通过自主梳理打折销售的相关知识,提升归纳、总结能力,养成良好的自我反思习惯;通过能否理智面对打折促销活动,提升学生的批判思维能力。
三、“U型”模式教学思考
本节课以学生的数学活动为主线,数学思考为核心,采用“U型”模式设计教学,体现了学生学习的主体性,实现了学习过程的完整性、规范性,丰富了学习经历。使学生更深入地掌握数学核心知识,领悟数学思想方法,发展数学核心素养。这种理性的精神、严谨的思维将使学生终身受益。
注:本文系陕西省教育科学“十四五”规划2021年度课题“基于深度教学的初中数学‘U型模式的实践研究”(SGH21Y0955)的研究成果。
作者简介:李云虎(1975—),男,中学高级教师,主要从事初中数学教学研究。
——基于商个人制度的研究

