新冠肺炎疫情冲击、劳动力市场波动与稳就业的财政规则

周磊 孙宁华 钱国军

内容提要：本文在包含搜寻摩擦的DSGE模型中考察了新冠肺炎疫情引致的水平冲击和不确定性冲击对劳动力市场波动的宏观影响和微观机理，量化分析不同财政政策规则“稳就业”的效果。研究表明：疫情冲击在短期内导致失业率上升和岗位空缺下降，其中，水平冲击与不确定性冲击的交互作用是劳动力市场波动的主要驱动力;水平冲击在供需两端的叠加作用加剧了失业，其在供需两端的抵消作用则降低了工资波动;不确定冲击通过预防性储蓄效应抑制了总需求，加剧了劳动力市场波动;在不同财政政策中，政府购买规则在短期内“熨平”劳动力市场波动的效果优于税收规则，但也造成了对私人消费的挤出。此外，财政政策的时滞制约了其“稳就业”功能的充分发挥。

关键词：新冠疫情冲击;劳动力市场波动;财政规则;搜寻摩擦;DSGE模型

中图分类号：F015;F240;F812  文献标识码：A  文章编号：1001-148X（2022）04-0043-15

收稿日期：2021-06-27

作者简介：周磊（1988-），男，安徽肥西人，中国银行博士后科研工作站在站博士后，经济学博士，研究方向：宏观经济、劳动经济与区域经济;孙宁华（1968-），男，河南固始人，南京大学经济学院教授，博士生导师，研究方向：宏观经济与中国经济发展;钱国军（1986-），男，安徽滁州人，南京大学经济学院博士研究生，研究方向：宏观经济与金融监管。

基金项目： 教育部人文社科重点研究基地重大项目，项目编号：19JJD790002。

新冠疫情使全球劳动力市场遭受重创，2020年第二季度，OECD国家的平均就业率较2019年第四季度下降了624%，美国的降幅甚至高达1283%。从国内数据来看，2020年第一季度，疫情全面爆发期间，城镇调查失业率高达58%，较2019年第四季度的513%上升了14个百分点。与此同时，企业招聘需求人数急剧下降，中国人民大学与智联招聘发布的《2020年第一季度中国就业市场景气报告》显示，该季度的企业招聘需求较2019年第一季度同比下降约25%，就业景气指数同比下降1488%。失业率上升，招聘需求下降的特征事实与贝弗里奇曲线（反映劳动力市场中失业与岗位空缺负向关系的曲线）的轨迹相契合，表明此次新冠疫情冲击下的失业由周期性因素主导，而非长期以来的结构性失业。新冠疫情冲击与经济下行压力的叠加作用无疑给居于“六稳六保”首位的就业带来了空前挑战。评估此次新冠疫情对劳动力市场的影响，厘清疫情冲击传导机制，制定行之有效的“稳保就业”政策是当前亟待解决的课题。

一、文献综述

国内学者多从供求角度阐述疫情冲击劳动力市场的传导渠道。都阳（2020）通過对城镇调查失业率、求人倍率（招聘岗位数/求职人数）以及通货膨胀率的综合分析发现，此次疫情造成的负面需求冲击使得失业具有明显的周期性特征，并提出政府在短期内应通过时效性强、便捷度高的收入支持计划来刺激消费，拉动就业[1]。黄群慧（2020）指出，疫情冲击对宏观经济的影响首先表现为隔离政策对劳动者行动限制而产生的要素供给约束，导致供给侧被动收缩。随着疫情的蔓延，需求侧的消费、投资和出口也会被动收缩，供需两类冲击的相互作用最终导致经济衰退[2]。

从现有研究来看，如何将新冠疫情冲击引入DSGE模型尚无明确模式。Mihailov（2020）在一个标准的新凯恩斯DSGE模型中引入不利的劳动力供给冲击（劳动力负效用冲击）作为新冠疫情冲击的代理变量。他区分了因社交隔离而造成临时性劳动力供给冲击和因病毒感染致死而造成的永久性冲击，并根据模拟结果指出永久性冲击造成的人均消费和产出损失最高可达15个百分点[3]。将新冠疫情冲击表征为负向的边际效用冲击或者正向的劳动负效用冲击具有一定的代表性，且有助于简化模型设定，但孤立引入二者之一都不是理想选择。对消费边际效用的负向冲击将导致总需求下降，引起空缺岗位的减少和失业率的上升。但总需求萎缩引起的价格水平下降明显有悖于疫情期间的经济现实。另一方面，对劳动力边际负效用的正向冲击将使劳动力供给曲线左移，短期内会造成工资和福利水平的上升，而这一点同样与实际情况不符。事实上，新冠疫情作为一种外源性冲击，同时具有总需求和总供给效应。两种效应对产出、消费、失业率等经济变量的影响存在叠加作用，但对工资水平、通胀率等变量的影响则存在抵消作用。为全面刻画新冠疫情造成的劳动力市场波动，本文同时引入了消费需求冲击和劳动力供给冲击。

除需求与供给冲击外，疫情引致的不确定性也引发了各界的高度关注。IMF在2020年4月发布的《世界经济展望》中提到疫情的持续时间和严重程度具有极大的不确定性，这也导致了全球增长预测的不确定性[4]。Baker et al （2020）指出，疫情爆发初期引致了“几乎各方面”的不确定性：病毒的传染性和致死性;医疗系统应对“挤兑”风险的能力;研发和推广安全有效疫苗的时间;社交隔离、市场锁定以及其他缓解和遏制策略的持续时间和有效性;疫情消退后经济的恢复速度;消费者支出方式的转变程度等[5]。疫情引致的不确定性冲击通过与消费需求和劳动力供给冲击的交互效应给劳动力市场和宏观经济带来了更大更持久的波动。为充分体现疫情引致的不确定性与供求冲击的交互作用，同时为避免引入多样化冲击造成分析上的冗余。本文将疫情冲击划分为两类：一类是水平冲击（Level Shocks），即直接作用于宏观经济变量的外生冲击，这类冲击属于一阶矩冲击，它包括负向的消费边际效用冲击和正向的劳动力供给负效用冲击;另一类是不确定性冲击（Uncertainty Shocks），此类冲击并不直接作用于经济变量本身，它们通过改变水平冲击的风险强度（标准差）影响微观经济主体的预期和决策，从而引起劳动力市场波动，这类冲击属于二阶矩冲击，通常也被称为风险冲击或波动率冲击。

在理论模型的构建方面，标准的新凯恩斯模型通过粘性工资设定引入劳动力市场摩擦，较好地解释了就业、劳动生产率的周期性特征[6]。然而，这种传统的设定方式只能说明劳动力供求和工作时间的自愿变动，无法刻画劳动力市场的失业动态[7]。Merz（1995）创造性地将Diamond-Mortensen-Pissarides（DMP）模型中的搜寻摩擦引入RBC模型，为分析失业的周期性波动提供了理论工具[8]。Krause & Lopez-Salido（2008）则进一步将搜寻匹配纳入新凯恩斯理论框架，由此揭示了搜寻摩擦、边际成本与通胀动态三者间的内在联系[9]。Mumtaz & Theodoridis （2019）在包含搜寻摩擦的新凯恩斯模型中研究了货币政策冲击对失业率、岗位空缺、就业市场匹配效率、工资等变量带来的内生不确定性[10]。为使理论模型更准确地刻画此次疫情下我国劳动力市场的周期性波动特征，本文在标准DSGE模型中引入了劳动力市场的搜寻摩擦，并对劳动力市场的匹配效率进行了内生化处理。此外，鉴于疫情冲击会导致家庭未来效用的不确定性，本文在终生效用函数的设定上引入了随机未来效用的确定性等价（Certainty Equivalent）。

二、理论模型

本文参考Merz（1995）[8]、Krause & Lopez-Salido（2008）[9]、Mumtaz & Theodoridis （2019）[10]理论模型的部分设定，构建了一个包含家庭、中间品厂商、最终品厂商、政府（包含中央银行和财政部）的四部门新凯恩斯DSGE模型。

（一）家庭部门

假定经济中存在大量同质且具有无限期寿命的家庭，他们均匀分布在0，1的连续统上，整个家庭部门可由一个代表性家庭来表征。代表性家庭的效用函数为CRRA型，其设定如下：

uCt，Lt=ζtC1-σCt-11-σC-χtL1+σLt1+σL（1）

其中，Ct为商品消费量，Lt为劳动力供给（家庭就业人数），σC为消费跨期替代弹性的倒数，σL为弗里希劳动力供给弹性的倒数，ζt为消费偏好系数，χt为劳动负效用（闲暇）的偏好系数。

新冠肺炎疫情下，政府的居家隔离政策，家庭为避免接触感染的谨慎消费动机以及全球疫情下的外需疲软都会作用于系数ζt而产生负向的消费需求冲击。假定ζt服从如下AR（1）过程：

lnζt=ρζlnζt-1-εζt，εζt～iidN0，σ2ζ（2）

其中，εζt为疫情引致的消费需求水平冲击，假定其服从期望为0，标准差為σζ的白噪声过程，ρζ为冲击的持续系数。

在疫情全面爆发时期，病毒感染人数的上升造成了劳动力直接损失，政府的抗疫行动引起了部分劳动力转岗至非生产部门，最主要的是政府采取严格的居家隔离政策，导致劳动力要素供给中断（黄群慧，2020）。此外，一些行业和单位则采取灵活上班、轮换值班、居家办公、网络办公等非充分就业方式复工。为刻画疫情在短期内引致的劳动力供给冲击，假定系数χt服从如下AR（1）过程：

lnχt=ρχlnχt-1+1-ρχlnχ0+εχt，εχt～iidN0，σ2χ（3）

式（3）中，χ0为闲暇偏好系数的稳态值。εχt为疫情引致的劳动力供给水平冲击，假定其服从期望为0，标准差为σχ的白噪声过程，ρχ为冲击的持续系数。

代表性家庭终生效用服从Epstein-Zin型递归偏好：

VFt=uCt，Lt+βEtVF1-γt+111-γ（4）

上式中，VFt为家庭终生效用的值函数，β为主观贴现因子，γ为相对风险厌恶系数。通常而言，家庭的终生效用等于当期效用（uCt，Lt）与预期未来效用值函数的贴现（βEt（VFt））之和。考虑到新冠疫情冲击使得家庭未来效用（消费与劳动力供给）具有不确定性，本文假定风险厌恶型家庭的随机未来效用存在一个确定性等价EtVF1-γt+111-γ，即在随机未来效用贴现之和中扣除风险溢价。

家庭的预算约束如下：

Ct+dtRt=1-τWtLt+1-LtB-SCt+dt-1πt+Πt（5）

其中，dt为家庭在t期购买的政府债券的实际价值，Rt为名义利率，Wt为实际工资，1-Lt为家庭的失业人数，B为政府向失业家庭提供的救济金，πt为通胀率，τ为扭曲性收入税率。Πt为中间品厂商向家庭一次性转移的超额利润。SCt为失业者搜寻工作的成本，它是失业者搜寻强度（寻找工作的努力程度）的非线性函数：

SCt=κsSσstσs（6）

其中，St为失业者的搜寻强度，σS为搜寻成本弹性，κs为搜寻成本系数。

定义t+1期贴现到t期的随机贴现因子：

βMt，t+1=VFt/Ct+1VFt/Ct=βζt+1ζtCtCt+1σCEtV1-γt+1γ1-γV-γt+1（7）

在预算约束下求解家庭终生效用最大化的一阶条件可以得到：

1Rt=βEtMt，t+1πt+1

1λtVFtLt=κsSσs-μt1-LtμUμtV1-μt（8）

式（8）的两个子式分别为债券的欧拉方程和搜寻强度的内生决定方程，其中，VFtLt为家庭每增加1单位劳动力供给而带来终生效用的边际值，λt为家庭预算约束的拉格朗日乘数（影子价格），在上式一阶条件下，λt=VFtCt。

（二）劳动力市场

劳动力市场存在搜寻摩擦，处于失业状态的求职者（假定不存在在职搜寻）需要与厂商发布的空缺岗位成功匹配，才能形成新的雇佣关系。匹配函数满足规模报酬不变的Cobb-Douglas形式：

Mt=StUtμV1-μt（9）

其中，Mt为匹配数量，Ut为求职者数量。现有文献通常将St表示为匹配效率，在无摩擦的理想环境下，St应等于1，表明劳动力市场中新增就业等于搜寻匹配的成功人数。现实中，劳动力市场的供求异质性、信息不完全等问题使得St偏离理想值。本文参考Merz（1995）的设定，通过引入搜寻强度，将匹配效率内生化。直观而言，劳动者的搜寻强度提高能够有效改善信息不完全等问题，从而提高匹配效率。

厂商雇佣劳动力的演化方程为：

Lt=1-δLLt-1+Mt（10）

其中，为Lt厂商在t期雇佣的劳动力数量，δL为每一期外生的岗位破坏率。处于失业状态的求职者数量为Ut=1-1-δLLt-1，它包含t-1期失业的劳动者数量（1-Lt-1）以及t-1期末因岗位破坏而失去工作的劳动者数量（δLLt-1）。本文将总劳动力数量标准化为1，因此，t期的失业率可表示为：URt=1-Lt。

为刻画劳动力市场的供求状况，本文引入市场紧度（Tightness）这一概念，它是岗位空缺数与求职者人数的比率，即劳动力市场中供求双方的相对数量：θt=VtUt。

从匹配函数和劳动力市场紧度中可以推导出失业者顺利找到工作的概率（下文简称：工作觅得率）：

pt=MUt=S-1tθt1-μ（11）

以及空缺岗位被填补的概率（下文简称：岗位填补率）：

qt=MVt=Stθ-1tμ（12）

式（11）-（12）表明，工作觅得率和岗位填补率内生于劳动力市场紧度和失业者的搜寻强度。当新冠疫情冲击导致市场紧度下降时，劳动力市场供给侧的“拥挤”程度随之上升，失业者顺利就业的概率降低，而企业的空缺岗位则更容易被填补。这种劳动力市场供求双方一侧数量增加给自身带来的“负外部性”以及给另一侧带来的“正外部性”被称为“搜寻外部性”（Merz，1995）。“搜寻外部性”是劳动力市场波动的一个重要传导机制，它通过与其他传导机制的叠加作用会放大疫情冲击的影响，造成更大更持久的失业问题。

（三）厂商部门

假定存在中间品和最终品两类厂商。中间品厂商在[0，1]的连续统上进行差异化生产，因此，具有垄断竞争的市场特性。完全竞争的最终品厂商将中间品打包，形成最终商品，出售给消费者。假定最终品由中间品的Dixit-Stiglitz加总得到：

Yt=∫10Yti-1di-1（13）

其中，Yt为最终品产量，Yti为中间品厂商i的产量，为中间品的替代弹性。由式（13）可得，最终产品厂商对中间品的需求函数为：

Yti=PtiPt-Yt（14）

中间品厂商的生产函数设定如下：

Yti=AtLtiφ（15）

其中，At为全要素生产率，Lt（i）为厂商i雇佣的劳动力数量，φ为劳动的产出弹性。本文主要聚焦于疫情冲击对劳动力市场的影响，为简化分析，此处忽略资本要素，在后续的敏感性分析中，本文将引入资本。

中间品厂商面临两阶段的最优化问题。在第一阶段，给定工资和发布空缺岗位的成本，厂商在雇佣劳动力演化方程（式（10））约束下，选择劳动力雇佣数量和空缺岗位发布数量来最大化终生利润的贴现。即：

Ft=maxLt（i），Vt（i）}Et∑

j=0Mt，t+jβjMCt+j（i）Yt+ji-Wt+jLt+ji-VCt+j（i）（16）

其中，MCt（i）为企业雇佣劳动力的边际成本。VCt（i）为厂商发布空缺岗位的成本，假定其为空缺岗位数量的非线性函数：

VCt（i）=κVVtiσVσV（17）

其中，σV>1为岗位空缺发布成本弹性，κV为空缺岗位发布成本系数。

求解中间品厂商第一阶段的一阶条件可得：

Θti=MCti1-φYtiLti-Wt+β1-δLEtMt，t+1Θt+1i（18）

Θt（i）=κVVtiσV-1qθt（19）

式（18）为中间品厂商每雇佣一单位劳动力的边际值（Θti=FtLt），即每填补一单位空缺岗位所带来的终生利润的值函数。式（19）为企业的岗位创造条件（Job Creation Condition）。整理式（18）和式（19）可得：

κVVtiσV-1发布空缺布岗缺边际成本=MCti1-φYtiLti-Wt+β1-δLEtMt，t+1Θt+1i填补空缺岗位的边际值qθt空缺岗位被填补的概率（20）

直观而言，企业发布的空缺岗位数量应该使每填补一单位空缺岗位带来的边际值乘以该空缺岗位被填补的概率（式（20）右侧）等于每增加一单位空缺岗位产生的边际成本（式（20）左側）。

在第二阶段，假定连续统中的中间品厂商在每一期仅有一定比例ξ可以调整价格，其余的厂商则延续上一期的定价。在每一期中，可自由调价的厂商在生产技术约束下，选择最优定价（P*ti）来最大化终生利润的贴现，即：

maxP*tiEt∑

j=0Mt，t+jβξjYt+jiP-1t+ji（22）

式（22）为中间品厂商的最优定价方程，对该式线性化可以得到新凯恩斯菲利普斯曲线（NKPC）。在均衡条件下，单个厂商加总成总体厂商，可消去个体符号i。

（四）工资决定

与大多数搜寻匹配文献一致，本文假定工资水平由家庭与厂商通过双边议价决定，即二者就劳动力市场中总剩余（Total Surplus）的分割进行纳什谈判。参考Krause & Lopez-Salido（2008）[9]的设定，纳什议价问题由下式所述：

WNasht=argmax1λtVFtLtηFtLt1-η（23）

其中，1λtVFtLt为家庭每增加1单位就业的终生收益贴现和，FtLt为企业雇佣一单位劳动力的终生利润贴现和。经济中的总剩余为：St=1λtVFtLt+FtLt。

由纳什议价条件可得劳动力市场总剩余的分配方案如下：

1-η1λtVFtLt=ηFtLt（24）

将式（8）、式（18）-（19）带入式（24）可以推出纳什议价下的均衡工资。

WNasht=ηMCt1-φYtLt+β1-δLEtMt，t+1Sμ-1t+1θ1-μt+1Θt+1+1-ηχtζtLσLtCtσC+B-SCt1-1-ητL（25）

上式表明，当劳动力市场存在搜寻匹配摩擦时，均衡工资会偏离劳动的边际收益产品（MCt1-φYtLt）。在双边谈判中，劳动者与厂商订立劳动合同时，会引入风险分担机制，以减轻工资波动对双方造成的损失。就厂商而言，他不仅要考虑当期的边际收益产品，还要考虑岗位空缺被填补时节省的成本。就劳动者而言，他不仅要考虑当期劳动的边际负效用（χtζtLσLtCtσC），还要考虑自身的外部选择权（失业救济金减去节省的搜寻成本）。议价权重η决定了工资与厂商或劳动者利益的接近程度。β1-δLEtMt，t+1Sμ-1t+1θ1-μt+1Θt+1的经济直觉是，如果谈判破裂，劳动者和厂商将不得不在下一期的劳动力市场中重新进行搜寻匹配，厂商节省下一期的空缺岗位发布成本（Θt+1）也应计入工资中。

（五）政府部门

政府通过征收扭曲性收入税和发行债券筹集资金，用于公共支出，清偿上一期债务以及发放失业救济金。政府预算约束如下：

Gt+1-LtB+dt-1πt=τWtLt+dtRt（26）

其中，Gt为公共支出，假定政府按GDP的固定比例（ω）进行支出，即Gt=ωYt。

假定中央银行根据通胀和产出缺口调整名义利率，货币政策服从如下泰勒规则：

RtR-=Rt-1R-ρRπtπ-φr，πYtY-φr，y1-ρR（27）

上式中，π-、Y-和R-分别为目标通胀率、稳态产出水平和稳态利率，ρR为利率调整的平滑系数，φr，π为通胀的反应系数，φr，y为产出缺口的反应系数。

（六）市场出清条件

经济中的总产出除用于消费和公共支出外，还有一部分用于厂商发布空缺岗位的成本以及失业者的搜寻成本。整体经济的资源约束条件如下：

Yt=Ct+Gt+VCt+SCt（28）

三、参数校准与估计

本文模型中的待估参数分为两类，一类是决定内生变量稳态值的行为参数，这类参数通常采用校准方法进行赋值;另一类是刻画内生变量动态变化特征的结构参数，对于此类参数，校准法因缺乏正式的统计基础而不适用（王曦等，2016），因此，本文采用贝叶斯方法对此类参数进行估计[11]。

（一）参数校准

参考Chang et al（2016）的做法，将主观贴现因子（β）校准为0996[12]。借鉴王曦等（2016）的设定，将消费的跨期替代弹性的倒数（σC）校准为2，将弗里希劳动力供给弹性的倒数（σL）校准为1。参考邓红亮和陈乐一（2019）、李亮亮（2020）的设定，将匹配弹性（μ）校准为05，岗位分离率（δL）校准为01，纳什议价参数（η）校准为05，政府支出占GDP的比重（ω）校准为014[13-14]。多数学者将劳动的产出弹性（φ）校准为05，本文沿用这一数值[15]。参考王博等（2019）的设定，将中间产品的替代弹性（）校准为10;参考许志伟和王文甫（2019）的设定，将稳态的收入税率（τ）校准为015[16]。

考虑到城镇登记失业率具有统计口径窄，发布频率低和时效性差等缺陷，存在低估真实失业率的问题。本文根据2018年1月-2019年12月（疫情全面爆发前）城镇居民调查失业率的平均值将稳态失业率校准为00504。

对搜寻成本、空缺岗位发布成本以及失业救济金的相关参数校准，国内文献涉及较少，综合Merz（1995）[8]、Krause & Lopez-Salido（2008）[9]和Mumtaz & Theodoridis（2019）[10]的设定，初步将κS，κV校准为005，将σS，σV校准为3，将失业救济金校准为01，后文将通过对上述参数的调整进行敏感性分析。此外，利用参数与内生变量的稳态关系将闲暇偏好系数χ0校准为044。

（二）贝叶斯估计

识别新冠疫情水平冲击的强度（标准差）和持续性对于量化分析疫情冲击下劳动力市场的波动程度至关重要。然而，此类突发事件的持续时间一般较短，宏观数据的时效性与样本量之间的矛盾是参数估计的一大挑战。保证数据的时效性需要以牺牲观测样本量为代价，而大样本又可能将疫情冲击的影响“摊平”。考虑到调查失业率和求人倍率（崗位空缺）等数据的样本量较小，且受季节因素影响，为协调二者的矛盾，本文使用了1992Q1-2020Q2的产出、消费、通胀、利率等观测数据（剔除季节因素），这一时段的数据中包含了新冠疫情冲击的新息，因此，用于估计疫情冲击的强度和持续性具有一定的科学合理性。

由于模型中仅涉及两个水平冲击项，而当观测变量个数大于冲击项个数时，估计过程将不可避免地出现随机奇异性。为避免这一问题，本文在观测方程中引入了测量误差。

此外，为保证观测数据与模型变量在经济意义上的匹配，本文采用对数差分方法对非平稳观测数据进行了去趋势处理，而非常用的HP滤波。事实上，HP 滤波提取数据波动成分的理论基础与 DSGE 模型的数据生成过程（Data Generating Process）并不匹配，且 HP 滤波在处理数据时会损失大量数据信息[17]，而这些信息对于识别疫情冲击至关重要。表2汇报了贝叶斯估计的结果。

四、数值模拟及机制分析

为研究新冠肺炎疫情冲击下劳动力市场波动的动态特征及其内生传导机制，本文首先考察了疫情引致的水平冲击的脉冲响应;随后，在水平冲击的基础上进一步使用三阶近似的扰动算法，分析了不确定性冲击的脉冲响应;最后，通过方差分解甄别了不同类型冲击在劳动力市场总体波动中的贡献程度。

（一）水平冲击

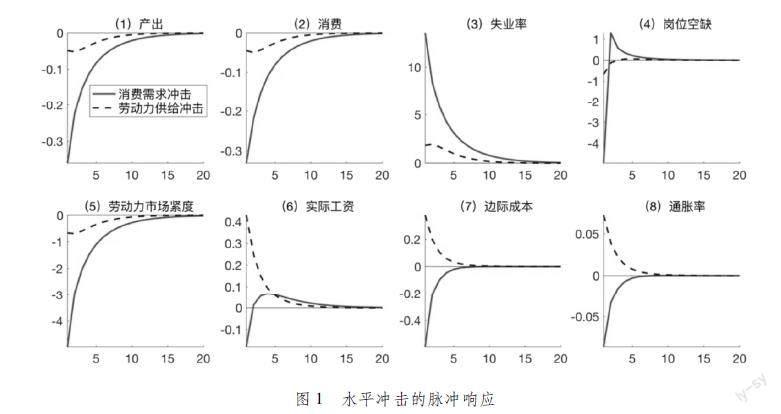
图1可知，疫情引致的负向消费需求冲击在短期内导致失业率大幅上升，与此同时，产出、消费、岗位空缺、实际工资等变量呈下降趋势。疫情全面爆发期间，政府的社交隔离和市场锁定政策使得即时性、接触性消费被动收缩，劳动力吸纳能力强的服务业等部门遭受重创，导致企业对劳动力的引致需求下降，部分既有岗位遭到破坏，失业率上升。此外，根据厂商的岗位创造条件（式（20）），消费需求（进而均衡产出）下降也减少了厂商创造新岗位的边际收益，导致空缺岗位供给减少，劳动力市场紧度下降，在搜寻外部性的作用下，失业者顺利就业的可能性（工作觅得率）下降，从而放大了疫情冲击对劳动力市场波动的影响。值得注意的是，在图1中，消费需求冲击会引起产品均衡价格和工资水平的下降，进而降低通胀率，这一点与疫情期间物价水平上涨的特征事实明显不符。由此可见，单一的需求冲击传导机制不足以充分解释疫情期间劳动力市场和宏观经济的动态变化特征。

在疫情引致的负向劳动力供给水平冲击下，失业率、实际工资和通胀率呈上升趋势，产出、消费、岗位空缺呈下降趋势，表明疫情引致的供给冲击诱发了短期滞胀。负向的劳动力供给冲击会导致劳动力供给曲线向左移动，一方面引起均衡就业水平下降（失业率上升），另一方面引起均衡工资上升，从而推高了厂商的边际成本，在短期内形成成本推动型通胀，这一传导机制解释了疫情期间物价水平的上涨。此外，与需求冲击类似，均衡工资上升也会降低厂商创造新岗位的边际收益，进而通过搜寻外部性传导机制进一步提高失业率。

图1 水平冲击的脉冲响应

综上所述，疫情引致的两种水平冲击从供求两端同时发力，对产出、消费、失业率的下降产生了叠加作用，并通过搜寻外部性这一渠道加剧了劳动力市场的波动;而两种水平冲击在实际工资、边际成本上的抵消作用则在一定程度上缓解了工资、通胀波动。此外，消费需求冲击对产出、消费和失业率的负面影响明显大于劳动力供给冲击，其主要原因是，在贝叶斯估计下，消费需求冲击的标准差和持续系数均大于劳动力供给冲击。

（二）不确定性冲击

为刻画新冠肺炎疫情引致的经济不确定性，本文参考Basu & Bundick（2017）[18]的设定，在上文的水平冲击（式（2）-（3））中进一步引入不确定冲击，具体设定如下：

lnXt=ρXlnXt-1+1-ρχlnX0UCX，t-1εXt，X∈ζ，χ（29）

UCX，t=1-ρUCXUCχ+ρUCXUCX，t-1+εXUCεXUC，t（30）

上式中，εXt为两种水平冲击。εXUC，t为不确定性冲击，该冲击会作用于时变波动率变量UCX，t从而改变水平冲击的标准差。直观而言，疫情不仅对消费需求与劳动力供给产生了水平冲击，其引起的不确定性也会改变水平冲击的分布形状（标准差），使得经济主体难以对经济形势形成准确预期，从而加剧了经济运行风险。经济学中通常使用方差度量风险和不确定性，因此，疫情引致的不确定性冲击可以理解为水平冲击方差的突然增大。

此处设定εXt和εXUC，t均服从期望为0，标准差为1的白噪声过程。参数UCX为水平冲击的无条件标准差，亦称均值波动率。当不确定冲击为0时，UCX，t=UCX，式（29）与式（2）-（3）等价，此时，UCζ=σζ，UCχ=σχ。由上文贝叶斯估计可知，UCζ为00113，UCχ为00077。参数εXUC和ρUCX分别表示不确定冲击的标准差和持续系数。

1.不確定性冲击的参数估计

校准（估计）参数εXUC和ρUCX是评估新冠疫情下不确定性冲击影响的必要前提。现有文献对不确定性参数的校准值缺乏疫情冲击的新息，因此不具有借鉴意义，而基于线性卡尔曼滤波的贝叶斯估计并不适用于波动率冲击的参数估计。为避免参数εXUC和ρUCX设定的随意性，本文在贝叶斯估计的基础上进一步引入了矩匹配这一新的估计方法。该方法假定理论模型与现实经济具有相同的数据生成过程，它通过在待估参数空间中选择一组参数，使观测变量的实际矩（Empirical Moment）与模型生成的模拟矩（Simulated Moment）之间的加权距离最小化。参数估计方程如下：

θ[DD（-*2/3][HT6”]^[][HT][DD）]=arg minθ∈Θ[Ψ[DD（-*2/3][HT6”]^[][HT][DD）]-Ψθ]′W-1[Ψ[DD（-*2/3][HT6”]^[][HT][DD）]-Ψ（θ）]

其中，Ψ[DD（-*2/3][HT6”]^[][HT][DD）]为观测变量的实际标准差，Ψ（θ）为不确定性冲击下的模拟标准差，θ（ρUCξ，εξUC，ρUCχ，εχUC）为待估参数向量，W=diag（Ψ[DD（-*2/3][HT6”]^[][HT][DD）]）为权重矩阵。与贝叶斯估计一致，本文选取了产出、消费、通胀和利率四个观测变量，表3汇报了矩匹配的估计结果。

由表3可知，除通胀外，其他观测变量的Kydland-Prescott（K-P）比率均接近于1，表明基于矩匹配方法的估计结果使理论模型较好拟合了实际经济。从估计参数来看，劳动力供给不确定性冲击的标准差和持续系数分别为00299和08998，高于消费需求不确定性冲击的00175和08782。由此可见，新冠疫情对劳动力供给不确定性的影响程度更大，持续性更久。

2.不确定性冲击的脉冲响应分析

为考察疫情引致的不确定性冲击对劳动力市场的影响，本文采用了三阶近似的扰动算法。一阶近似下的确定性等价问题使得波动率冲击对内生变量没有影响，二阶近似会导致水平冲击与波动率冲击效应的交互，只有三阶近似能够分离出纯粹的波动率冲击效应[19-20]。此外，为避免高阶近似下随机模拟的爆炸路径问题，本文采用了剪枝算法（Pruning）。图2汇报了不确定性冲击的脉冲响应。

由图2可知，新冠疫情引致的两种不确定性冲击对主要经济变量的作用方向是相同的，二者均造成了失业率上升，同时也引起了岗位空缺、劳动力市场紧度和实际工资的下降。由此推断，两种不确定性冲击的内生传导机制具有一致性。相比水平冲击，不确定性冲击对劳动力市场造成的波动较小。此外，由于两种不确定性冲击的标准差和持续系数差异，劳动力供给的不确定性对劳动力市场的负向冲击更大，持续性更久。

不确定性影响劳动力市场的主要机制是预防性储蓄效应（Precautionary Savings），即不确定性上升时，家庭会减少消费，增加储蓄，以应对消费波动。产生这一效应的原因是风险厌恶型家庭的效用函数具有凹性。根据詹森不等式，消费的期望效用（EU（C））小于期望消费的效用（U（E（C））），因此，家庭的期望效用存在一个扣除风险溢价的确定性等价。图3给出了这一效应的直观理解：假定存在两种随机消费分布[C1，C2]和[C1′，C2′]，它们有相同的期望E（C），但后者的方差大于前者。当不确定性上升时，消费分布由[C1，C2]转换为[C1′，C2′]，期望效用的确定性等价也由AD转变为BD′，导致其对应的消费下降。

在疫情爆发初期，感染率、致死率以及隔离政策的持续时间等不确定性因素导致了劳动者就业和收入的不确定性，在我国疫情得到全面控制之际，境外输入病例的风险不容小觑。不确定性使消费者的信心受挫，形成悲观预期，风险厌恶的家庭出于谨慎动机会减少当期消费，以达到平滑消费的目的。预防性储蓄效应进一步降低了总需求以及厂商对劳动力的引致需求，导致失业率上升，岗位空缺下降，加剧劳动力市场波动。

值得注意的是，在图2中，总需求与边际成本下降的同时，通胀率却呈上升趋势，这一结果似乎有悖直觉。事实上，在新凯恩斯模型中，由于粘性价格设定，可自由调价的厂商在面临不确定性时会选择高价（高边际成本加成）策略，以实现预期收益最大化。如果厂商选择低价，当期销量会上升，但粘性低价和未来需求的不确定性会降低厂商预期收益（或扩大厂商预期损失）。在不确定性环境下，厂商的高价决策推高了通胀水平。

（三）疫情冲击的方差分解

上文的脉冲响应分析单独考察了疫情引致的水平冲击和不确定性冲击对劳动力市场波动的影响程度和传导机制。疫情期间，劳动力市场波动的主要驱动力是什么呢？为甄别各类冲击对总体波动的贡献程度，有必要对失业率、岗位空缺、实际工资等主要经济变量进行方差分解。值得注意的是，在三阶近似下，模型的策略函数中包含了非线性项，因此，总体方差不能表示为各冲击贡献额的简单线性加总，一种可行的做法是：将部分冲击控制为0，以此测度所要考察的冲击造成的波动[21]。

本文考察了六种可能的冲击组合。第一种是总水平冲击（εζt+εχt），第二、三种是单独的消费需求（εζt）和劳动力供给水平冲击（εχt），第四种是总不确定性冲击（εζUC，t+εχUC，t），第五种是消费需求的水平与不确定性冲击组合（εζt+εζUC，t），第六种是劳动力供给的水平与不确定性冲击组合（εχt+εχUC，t）。表4汇报了方差分解的结果。

表4显示，纯粹的水平冲击和不确定性冲击对总体波动的贡献度较小。其中，总水平冲击（εζt+εχt）仅解释了工资波动的115%，对失业率波动的解释力度也只有553%。相比水平冲击，总不确定性冲击（εζUC，t+εχUC，t）对劳动力市场波动的解释力度更小，其引起的产出和失业率波动仅占水平冲击的092%和093%。

在水平冲击中，消费需求冲击是产出、消费、失业率、岗位空缺等变量波动的主要推动力。其中，消费需求冲击造成失业率波動为11009，而劳动力供给冲击对应的波动仅为00314。值得注意的是，在冲击标准差和持续系数均小于消费需求冲击的情形下，劳动力供给水平冲击引起的工资波动（00564）却大于消费需求水平冲击（00101），可能的原因是劳动力供给冲击直接作用于均衡工资，而消费需求冲击则通过劳动力的引致需求间接影响工资水平，这种间接传导机制弱化了消费需求变动对工资冲击效应。此外，由于两种水平冲击对实际工资的作用方向相反，冲击效应的相互抵消降低了总水平冲击（εζt+εχt）下的工资波动（00462），这一点也印证了前文中水平冲击的脉冲响应分析。

水平冲击与不确定性冲击的组合冲击是劳动力市场波动的主要推动力。其中，消费需求的水平与不确定性组合冲击（εζt+εζUC，t）引起的产出和失业率波动分别为25561和99587，解释了总产出波动的4330%和总失业率波动的5417%;劳动力供给的水平与不确定性组合冲击（εχt+εχUC，t）解释了总产出波动的1217%和总失业率波动的1262%。由表4可知，水平与不确定性的组合冲击造成的波动远大于纯粹水平冲击与纯粹不确定冲击波动的简单加总。造成这一现象的主要原因是：在三阶近似中，水平冲击与不确定性冲击的交叉项进入模型的策略函数（Policy Function）。其经济直觉是：不确定性上升会强化水平冲击的传导机制，放大冲击的波动效应，反之亦然。由此可见，水平冲击与不确定性冲击的交互效应在劳动力市场总体波动中起主导作用。

（四）敏感性分析

前文根据国外相关文献对搜寻成本和空缺岗位发布成本的相关参数进行了初步校准。为进一步检验模型对这些参数的敏感性，本文比较了不同参数取值对模拟结果的潜在影响。此外，本文在模型中重新引入资本与投资两个内生变量，以考察模型设定的稳健性。结果表明，在不同的参数取值与模型设定下，产出、消费、失业率等核心变量的脉冲响应图形状及大小顺序与基准模型类似，仅在模拟数值上存一些差异。由此可见，模型对上述参数和设定并不敏感，模拟结果较为稳健。

五、稳就业的财政规则

在新冠肺炎疫情冲击叠加经济下行压力的背景下，财政政策势必成为“稳就业”的重要调控手段。通常而言，財政政策具有被动（自动稳定器）和主动（相机抉择）两种调控方式。其中，自动稳定器借助累进税率和政府转移支付的“逆周期”变动影响居民收入和消费，进而降低外部冲击造成的经济波动。长期以来，我国税收体系的累进性较弱[22]，严重制约了自动稳定器功能的发挥，“逆风向”的主动调控一直是财政政策的主流。基于这一原因，本文重点考察积极的财政政策在“稳就业”方面的效果。现有研究通常将自动稳定器规则设定为转移支付对产出缺口的反应函数[23]。为剔除自动稳定器效应，本文在式（8）中将政府转移的失业救济金设定为一个常数，而非产出缺口的反应函数。本文主要考察三类政策规则：第一类是政府购买规则，第二类是税收规则，第三类是前两类规则的组合。

规则1：政府购买规则

参考胡永刚和郭长林（2013）[22]、朱军（2019）[24]的设定，假定政府购买性支出服从连续支出与相机抉择：

GtG-=Gt-1G-ρgYt-1Y-φG，Y1-ρg

其中，G-为政府购买性支出的稳态值，为保证与前文设定的一致性，假定G-=ωY-。φG，Y为政策对产出缺口的反应系数（政策反应弹性），在“逆周期”的调控下，该系数小于0。考虑到财政政策存在时滞，假定政府购买规则对滞后一期的产出缺口做出反应。

规则2：税收规则

与政府购买规则的形式类似，税收规则的设定如下：

τtτ-=τt-1τ-ρτYt-1Y-φτ，Y1-ρτ

其中，τ-为税率的稳态值，采用前文的校准值。ρτ为税率调整的持续系数，φτ，Y为税率对产出缺口的反应系数，该系数小于0。

规则3：组合规则

财政政策目标能否实现既依赖于政策刺激的强度，又依赖于政策的组合[23]。考虑到单一政策规则的局限性，本文同时考察了政府购买规则与税收规则的政策组合。

（一）脉冲响应比较分析

为便于比较上述三种财政规则“稳保就业”的效果，本文将三种政策规则的持续系数和对产出缺口的反应系数分别设定为相同的数值。图4汇报了不同政策规则下，疫情引致的水平冲击的脉冲响应函数。

由图4可知，相比基准模型，三种财政规则在短期内均有效抑制了水平冲击造成的产出下降和失业率上升。在相同的政策反应弹性和持续系数下，增加政府购买性支出的政策效果优于减税规则，两种政策组合的“稳就业”效果最好。造成这一情况的主要原因是：政府购买规则直接拉动总需求，增加了企业对劳动力的引致需求和新岗位的供给，提高了求职者的工作觅得率，降低了失业率。而减税政策通过改善家庭收入状况，缓解流动性压力，一方面增加了总需求，另一方面也提高了闲暇的边际成本，降低了劳动力供给的边际值和失业者搜寻工作的积极性（搜寻强度），从而降低了劳动力市场的匹配效率和工作觅得率，一定程度上削弱了“稳就业”的效果。

由图4的子图1-2和子图2-2可知，税收规则有效减缓了私人消费的下行压力，而政府购买规则使私人消费的降幅较基准模型更大，可见，“逆周期”的政府购买规则会导致经济资源从私人部门流向公共部门，对私人消费产生了明显的挤出效应，而两种政策组合能够在一定程度上中和政府购买规则的挤出效应。

值得注意的是，在疫情爆发的初始时点，不同财政规则下的产出、消费与失业率变化幅度与基准模型大体一致，表明疫情冲击初期，财政政策并未有效缓解劳动力市场波动，其主要原因是财政规则对经济波动的响应存在时滞。事实上，财政当局在识别疫情冲击上认知时滞，抗疫政策的制定和执行时滞，都会影响政策效果，如果将政策规则设定为对产出缺口的即期反应，财政政策在疫情冲击的初始时点也能较好的平抑劳动力市场波动。需要指出的是，上述“逆周期”的财政政策将不可避免地使政府转向债务融资，例如政府预计发行总计一万亿抗疫特别国债，赤字的增加将不可避免地提高政府未来的债务负担。

（二）财政乘数效应

为进一步量化分析疫情冲击下不同财政规则“稳保就业”和稳定经济的长期效果，拓展了长期贴现财政乘数。常规财政乘数仅考察政策执行期的产出拉动效应，忽略了后期经济主体的预期与应对措施，且难以捕捉政策的滞后效应，而长期贴现财政乘数在一个较长观测期内考察GDP与财政支出的动态路径，可有效规避上述问题（Faria-e-Castro，2018）[25]。本文按是否包含政策规则区分了两类模型，通过比较疫情冲击下两类模型相应变量的脉冲响应差异计算该乘数。长期贴现财政乘数的设定如下：

MPTω=∑Tt=1∏tj=1R-1jXStimulust-XNo Stimulust∑Tt=1∏tj=1R-1jSpendingStimulust-Spending No Stimulust

上式中，ω为各类财政规则，T为乘数效应的观测期，与前文脉冲响应分析一致，此处设定为20期。Xt为主要经济变量（产出、消费、失业率），上标Stimulus和No Stimulus分别表示有无财政规则的模型。Spendingt为政府财政支出（本文中减税也被视为一种财政支出），Rj为j期名义利率，鉴于不同财政规则模型中的Rj存在差异，为便于比较，此处使用基准模型中的Rj。

不同冲击对宏观经济的影响程度和传导机制存在差异，因此，其对应财政规则的乘数效应也不尽相同。鉴于此，本文考察了供求两类冲击下的乘数效应。此外，考虑到纯粹不确定性冲击的影响相对较小，本文重点分析水平冲击下的乘数效应。表5汇报了各种政策工具的长期乘数效应。

表5显示，在应对疫情引致的不同类型冲击时，政府购买规则的乘数效应存在显著差异。需求冲击下，政府购买规则对失业率的长期“熨平”效应是劳动力供给冲击下的217倍，而它对消费的长期挤出效应是劳动力供给冲击下的194倍。相比而言，税收规则和组合规则在两种冲击下对主要经济变量的乘数效应差距较小。

对比税收规则和政府购买规则不难发现，两种冲击下，减税对就业和产出的长期拉动效应强于政府购买。例如，劳动力供给冲击下，税收規则“熨平”失业率的乘数效应是政府购买规则的338倍。此外，税收规则对消费存在长期拉动效应，因此，减税可有效弥补政府购买规则的消费挤出效应。

组合规则拉动产出和降低失业的长期乘数效应高于政府购买规则，低于税收规则。例如，在消费需求冲击下，每增加1单位组合支出（政府购买+减税），产出提高了04906个单位，而增加政府购买和减税分别使产出提高了04706和06911个单位。

（三）福利损失分析

上文通过脉冲响应和财政乘数细化分析了疫情冲击下不同财政规则对主要经济变量的影响，但上述分析缺乏对社会整体福利水平影响的比较研究。鉴于此，本文参考郭豫媚（2016）[26]的研究，引入了社会福利损失函数，其设定如下：

Losst=VarY+ΩVar（π）

其中，VarY和Var（π）分别为产出和通胀的方差。参数Ω=05为权重系数。表6汇报了不同财政规则的福利损失。

由表6可知，基准模型下，疫情冲击造成的全社会福利损失为60108，政府购买规则下的福利损失为43852，较基准模型下降了2705%。税收规则下的福利损失为41933，比政府购买规则低3024%。两种财政规则组合下的福利损失最小，较基准模型下降了4607%。综合来看，组合规则在短期内熨平劳动力市场波动，长期中能有效抑制政府购买规则的消费挤出效应，其在减少社会福利损失方面的效果最好。

六、结论与政策启示

本文在包含搜寻匹配摩擦的DSGE模型中考察了新冠肺炎疫情冲击对劳动力市场波动的宏观影响和微观机理。得出如下研究结论：第一，短期内，疫情引致的水平冲击与不确定性冲击的交互效应是劳动力市场波动的主要驱动力，其中，消费需求的组合冲击解释了失业率波动的5417%，劳动力供给的组合冲击解释了失业率波动的1262%。而纯粹的水平冲击和不确定性冲击对劳动力市场波动的贡献率相对较小。第二，在疫情引致的水平冲击中，消费需求冲击占主导地位。消费需求与劳动力供给双向冲击的叠加作用加剧了失业率、岗位空缺以及劳动力市场紧度的波动，而供需冲击的抵消作用则在一定程度上减缓了工资和通胀的波动。第三，消费需求与劳动力供给两种不确定性冲击的传导机制具有内在一致性，即通过风险厌恶家庭的预防性储蓄效应削弱总需求，加剧劳动力市场波动。第四，劳动力市场的搜寻匹配摩擦是疫情的重要传导机制，搜寻外部性放大了疫情对劳动力市场造成的波动。第五，在相同的政策持续系数和反应弹性下，政府购买规则在短期内“熨平”劳动力市场波动的效果优于税收规则，但也造成了对私人消费的挤出，长期来看，税收规则的乘数效应大于政府购买规则，综合而言，组合规则“稳保就业”的同时造成的社会福利损失最小。此外，财政政策的时滞制约了其“稳保就业”功能的充分发挥。

根据上述结论，本文得到如下政策启示：第一，构建应对外源性冲击的就业保障政策体系，建立起财政政策、货币政策与就业政策的联动机制。短期内要提高政策的响应速度和落实效率，减少时滞。第二，调控政策要从供需两端同时发力，一方面加大对受疫情冲击损失较大的中小企业的支持力度，协助企业全面复产复工，降低劳动力供给冲击的负面影响;另一方面进行逆周期的宏观调控，提振总需求，以此拉动就业。第三，在推进稳就业政策的过程中应强调“稳预期”，注重“前瞻性指引”，以此提振家庭的消费信心，弱化不确定性冲击及其与水平冲击交互效应给劳动力市场带来的负面影响。第四，建立健全劳动力市场信息发布渠道，降低劳动力市场中信息不完全等摩擦因素，提高求职者与空缺岗位的匹配效率，以此降低搜寻匹配摩擦对疫情冲击的放大作用。

参考文献：

[1] 都阳.新冠病毒肺炎“大流行”下的劳动力市场反应与政策[J].劳动经济研究，2020，8（2）：3-21.

[2] 黄群慧.新冠肺炎疫情对供给侧的影响与应对：短期和长期视角[J].经济纵横，2020（5）：46-57，2.

[3] Mihailov， A. Quantifying the Macroeconomic Effects of the COVID-19 Lockdown： Comparative Simulations of the Estimated Galí-Smets-Wouters Model （No. em-dp2020-07）. Henley Business School， Reading University，2020.

[4] 易行健.新冠肺炎疫情对经济金融的冲击研究——基于国际文献综述及其扩展分析[J].金融经济学研究，2020，35（3）：3-16.

[5] Baker， S. R.，Bloom， N.，Davis， S. J.， et al.  Covid-induced Economic Uncertainty[R].NBER Working Papers.，2020.

[6] Christiano， L. J.，Eichenbaum， M. S.， & Trabandt， M. Unemployment and Business Cycles[J].Econometrica， 2016，84（4）：1523-1569.

[7] Blanchard， O.J， Galí， J. Labor Markets and Monetary Policy： A New Keynesian Model with Unemployment[J].American Economic Journal： Macroeconomics，2010，2 （2）：1-30.

[8] Merz， M. Search in the Labor Market and the Real Business Cycle[J].Journal of Monetary Economics，1995，36（2）： 269-300.

[9] Krause， M. U.，Lopez-Salido， D.， & Lubik， T. A.Inflation Dynamics with Search Frictions： A Structural Econometric Analysis[J].Journal of Monetary Economics，2008，55（5）：892-916.

[10]Mumtaz， H.， &Theodoridis， K.  Dynamic Effects of Monetary Policy Shocks on Macroeconomic Volatility[J].Journal of Monetary Economics，2019.

[11]王曦，王茜，陳中飞.货币政策预期与通货膨胀管理——基于消息冲击的DSGE分析[J].经济研究，2016，51（2）：16-29.

[12]Chang， C.， Chen， K.， Waggoner， D. F.， et al. Trends and Cycles in Chinas Macroeconomy[R].NBER Macroeconomics Annual，2016，30（1）：1-84.

[13]邓红亮，陈乐一.劳动生产率冲击、工资粘性与中国实际经济周期[J].中国工业经济，2019（1）：23-42.

[14]李亮亮.中国劳动力市场就业与真实工资的动态波动[J].财贸研究，2020，31（2）：1-17，79.

[15]Song， Z.， Storesletten， K.， & Zilibotti， F. Growing Like China[J].American Economic Review， 2011，101（1）：196-233.

[16]许志伟，王文甫.经济政策不确定性对宏观经济的影响——基于实证与理论的动态分析[J].经济学（季刊），2019，18（1）：23-50.

[17]孟宪春，张屹山，张鹤，等. 预算软约束、宏观杠杆率与全要素生产率[J].管理世界，2020，36（8）：50-65.

[18]Basu， S.， & Bundick， B. Uncertainty Shocks in a Model of Effective Demand[J].Econometrica， 2017，85（3）：937-958.

[19]Born， B.， & Pfeifer， J. Policy Risk and the Business Cycle[J].Journal of Monetary Economics，2014，68：68-85.

[20]王博，李力，郝大鹏.货币政策不确定性、违约风险与宏观经济波动[J].经济研究，2019，54（3）：119-134.

[21]Fernández-Villaverde， J.， Guerrón-Quintana， P.， Rubio-Ramirez， J. F.， et al. Risk matters： The Real Effects of Volatility Shocks. American Economic Review，2011，101（6）：2530-61.

[22]张佐敏.财政规则与政策效果——基于DSGE分析[J].经济研究，2013，48（1）：41-53.

[23]胡永刚，郭长林.财政政策规则、预期与居民消费——基于经济波动的视角[J].经济研究，2013，48（3）：96-107.

[24]朱军.高级财政学Ⅱ—DSGE的视角及应用前沿：模型分析与编程[M].上海：上海财经大学出版社， 2019：72-73.

[25]Faria-e-Castro， M. Fiscal Multipliers and Financial Crises[R].FRB St. Louis Working Paper， 2018：23.

[26]郭豫媚，陈伟泽，陈彦斌.中国货币政策有效性下降与预期管理研究[J].经济研究，2016，51（1）：28-41，83.

The Shocks of COVID-19 Pandemic， Labor Market Fluctuation and Fiscal Policy

Rules for Stable Employment——DSGE Model Based on Search Friction

ZHOU Lei1，2，SUN Ning-hua2，QIAN Guo-jun2

（1.Post-Doctoral Research Station， Bank of China， Beijing 100818， China;

2.School of Economics， Nanjing University， Nanjing 210093，China）

Abstract：This paper uses the DSGE model including search matching friction to evaluate the macro-impacts and micro-mechanisms of various shocks caused by the pandemic on the labor market and compare the employment stability effects of different fiscal policy rules. The results show that： the pandemic has caused the rise of the unemployment rate and the decrease of job vacancies in the short run. The interaction effect between level shocks and uncertainty shocks caused by the pandemic is the main driving force of labor market fluctuation. The superimposed effect of level shocks on both sides of supply and demand intensifies the fluctuation of the unemployment rate and job vacancies， and its counteracting effect reduces the fluctuation of wage. Uncertainty shocks suppresses aggregate demand through precautionary savings effect， exacerbated labor market fluctuation. In the short run， the impact of government purchase rule on smoothing labor market fluctuation is better than that of tax rule， but it also results in crowding out of private consumption. In addition， the time lag of fiscal policy restricts the full play of its stable employment to a certain extent.

Key words：COVID-19 pandemic; labor market fluctuation; fiscal rules;search friction; DSGE model

（責任编辑：周正）