引导学生把握好学习的“关键性步子”

王建芹

[摘 要]学生若能在学习过程中把握好“关键性步子”，那么他们就会稳健从容，从而使得学科素养的培养落地生根。文章以“用数对确定位置”为例，借助学生熟悉的学习情境、位置的确定过程和数对的产生过程，引导学生把握好数对学习的“关键性步子”，体会数对在确定位置中的作用，同时渗透坐标知识，为图形与坐标的学习打好基础。

[关键词]关键性步子;数对;确定位置

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）14-0046-03

在一次全县教学研讨会上，笔者执教了四年级下册“用数对确定位置”一课。“用数对确定位置”是学生在已学过用类似“第几排第几个”的方式描述物体在平面上的位置，从而获得用自然数表示位置的方法的基础上学习的。本课结合具体的座位图情境，引导学生学会用数对来表示位置，理解数对在确定位置中的作用，为第三学段“图形与坐标”的学习打好基础。

备课时，笔者侧重表达数学形式的统一规定，即列与行的确定和数对的表示都是为了表达需要，所以要形式上统一。试教时，学生都能在“规定”的引领下进行数学形式的表达，一节课下来，学生感觉数对知识非常简单，既知道了数对的作用，又会用数对表示平面上物体的位置，而笔者在课堂上的表现也相当精彩。评课教师这样说：“王老师的声音甜美动听，语言生动丰富;教学过程丝丝入扣，层层递进;目标达成顺畅自然，水到渠成。”试教结束，笔者收获诸多好评，内心有几分窃喜，为自己的付出得到同行的认可而高兴。

后来，在整理教案和反思教学过程时，笔者忽然觉得这样的课堂似乎少了点什么。本课研究的是将物体（点）放在直角坐标系的第一象限内来确定其位置。学生虽然是第一次“近距离”接触平面直角坐标系，但类似的知识经验在以往的學习中是否有过？如何链接原认知？怎样为以后的学习做好铺垫？这节课最有价值的探究点在哪？在学习过程中，学生除了获得知识与技能，还有哪些素养应该发展？教学的路径在自我追问中渐进明朗，带着贲友林老师倡导的“学为中心”的理念，笔者把原有的教学设计全部“清零”，重新思考，进行二次备课。

二次备课时，笔者查阅了大量的资料，了解了人类用数对确定位置的大致历程后，把本课的教学重点定位在引领学生把握好数对确定位置的“关键性步子”，抽象出更为简洁的数学化表达。这样操作，能帮助学生理解“用数对确定位置”规定背后的合理化，带领学生找到数学知识的落脚点和生长点。

【教学实践】

1.一维的位置确定

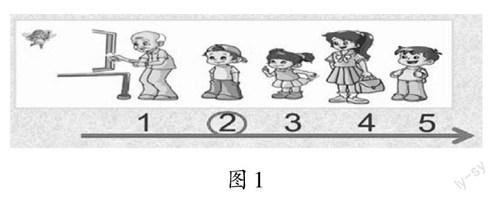
师（出示课题）：在一年级时我们就接触了确定位置。（边说边点击如图1所示的课件）戴帽子的男孩排在第几？你是怎么数的？

生1：第2，从左往右数。

师：老师用箭头表示你数的方向，如果用一个数来表示他的位置，是几？

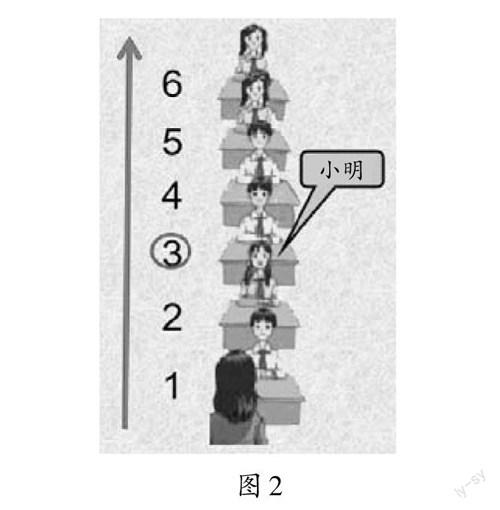
师（边说边点击如图2所示的课件）：小明的位置在哪？

生2：从前往后数第3个。

师：说得非常完整！若用一个数表示，是几？

师（小结）：像这样只有一排或一列时，要确定其中某个位置，用几个数就可以了？（学生回答略）

2.二维的位置确定

师（课件出示图3）：如果有很多排，又该怎样确定位置？

（1）初步建立直角坐标系

师：小明的位置在哪？先独立思考，再想一想、找一找。

师：如果有答案，别急着说，拿出学习单（如图4），根据提醒，在上面画一画、标一标，找到小明的位置。

（2）明确列、行及其数的方向

师：说说你是怎么找的。

生1：先从左往右数第4排，再从前往后数第3个，小明的位置在第4排第3个。

生2：先从右往左数第3排，再从前往后数第3个，小明的位置在第3排第3个。

生3：先从左往右数第4组，再从前往后数第3个，小明的位置在第4组第3个。

……

师：为什么同一个位置会有不同的表达方式？

生4：方向不同，表达方式不同。

师：说法不统一，这样交流起来方便吗？为了方便交流，我们通常把竖排叫作“列”，横排叫作“行”。

师：小明在哪一列？

生5：第4列。（根据学生回答，教师用记号笔在学习单的第4列上画竖线）

师：行呢？怎么数？大家数一数共有几行？（学生用手势比画）

师：小明在第几行？

生6：第3行。（根据学生回答，教师用记号笔在学习单的第3行上画竖线）

师：那小明的位置在哪？用数学语言来表达。

生7：第4列第3行。

师（指着位置图上的一个男孩）：他的位置怎么表述？

生8：第2列第1行。

（3）将位置图抽象成圆点图

师：如果把位置抽象成圆点，你还能找到小明的位置吗？（把位置图变成圆点图）

师：先找什么？怎么数？（根据学生回答，课件依次出现列、行，如图5）

（4）抽象出数对

师：谁能用比“第4列第3行”更简洁的方式来表示小明的位置？先想一想，再在作业本上写一写。（指名学生板书）

生1：4、3。

生2：4.3。

生3：4，3。

师：我们看黑板上这几个同学写的数据，它们非常的相似，它们都有哪两个数？4和3表示什么？

生4：都有4和3，4和3表示第4列第3行。

师：很棒！抓住了关键的第4列第3行。

师：为了让各个国家的人都明白它的意义，数学家和你们的想法是一致的，保留了最关键的4和3，并用逗号隔开，又在两边加上小括号，表示这是一个整体（教师边说边板书）。它有个好听的名字，叫作“数对”。

师：既有列又有行时，我们用几个数来确定位置？分别表示什么？（学生回答略）

3.三维的位置确定

依次出示图6、图7和图8：

师：只有一行时，我们用一个数来确定位置（如图6）;既有列又有行时，我们用两个数来确定位置（如图7）;如果是如图8这样的，又该怎样确定位置呢？（学生回答略）

【教学思考】

“用数对确定位置”既是对学生原有确定物体位置认知经验的深化，又承担着为后续学生学习坐标与函数奠基的任务。本课引导学生从生活实际中感受位置确定的方法，体会数对在确定位置中的作用，让学生能用数对表示平面图上某一点的位置，初步感知坐标的知识，为今后学习坐标打好基础。

赫斯说：“对学科本质的认识和了解是一切教学法的根。”对教师而言，把握教学之根，就要立足教材，关注知识本质。用数对（a，b）表示物体在平面中的位置，其实质是“在直角坐标系中，对于平面上的任意一点，都有唯一的一个有序数对与它对应;反过来，对于任意一个有序数对，都有平面上唯一的一点与它对应”。在本课中，学生经历了数对表示位置的发展过程，从中把握了“关键性步子”。

1.熟悉的学习情境

奥苏贝尔曾说：“如果我不得不把教育心理学的所有内容简约成一条原理的话，我会说：影响学习的最重要的因素是学生已知的内容，弄清了这一点后，进行相应的教学。”课始，我从戴帽子的男孩这一熟悉的学习情境导入，在学生根据已有的认知经验，用一个数便能轻松、准确地表示出某一位置后，再抛出“如果有很多排，又该怎样确定位置？”这一核心问题，直击知识核心，打开新旧知识的链接點，驱动学生思维由一维向二维发展。

2.位置的确定过程

为了让学生把握好从一维到二维再到三维位置确定中的“关键性步子”，教学时笔者充分放手：首先，从学习单上的画一画、标一标开始，引导学生勾勒出直角坐标系的原始轮廓，建构初步表象;其次，在点图上用列和行交叉的点表示小明的位置，激发学生从二维空间的视角思考，发现可以用两个数表示小明的位置;最后，给出任意空间内的一个点，引导学生思考如何确定它的位置，让学生感受到数学知识间的紧密联系、层层深入，以及数学学习的深刻性和规律性。

3.数对的产生过程

围绕“小明的位置在哪？”这一问题，学生通过对同一位置的不同表达，从准确性与必要性出发，把握了位置表达的“关键性步子”，同时也深刻地理解了一些数学规定背后的“合理性”。当教师提出“谁能用比‘第4列第3行更简洁的方法来表示小明的位置？”这一问题时，抓住“关键的数”来确定位置应运而生。于是，当既有列又有行时，数对最本质的特征在思维的碰撞中得以抽象、重现，学生完整地经历了数对“自主化”产生的过程，透彻理解了数对中两个数表示的意义。这一过程是逐步递进、简化、抽象的，学生从中体会到“数对”在确定位置中的作用，感受到数学的简洁性与抽象性。

位置确定，从一维到二维再到三维，又从座位图到圆点图再到方格图，双线并行，层层递进，数形结合，渗透了“坐标”思想，为学生今后学习坐标打好基础。只有把握好学习的“关键性步子”，学生才能将视野从平面上的点拓展到空间中的点，也才能走得稳健从容，使得学科素养的培养落地生根。

[本文系江苏省教育科学“十三五”规划立项课题“基于核心素养的小学数学‘三线五步教学模式的研究”（课题编号：D/2016/02/138）的研究成果之一。]

（责编 黄春香）