从制作无盖的长方体纸盒说起

赵娟

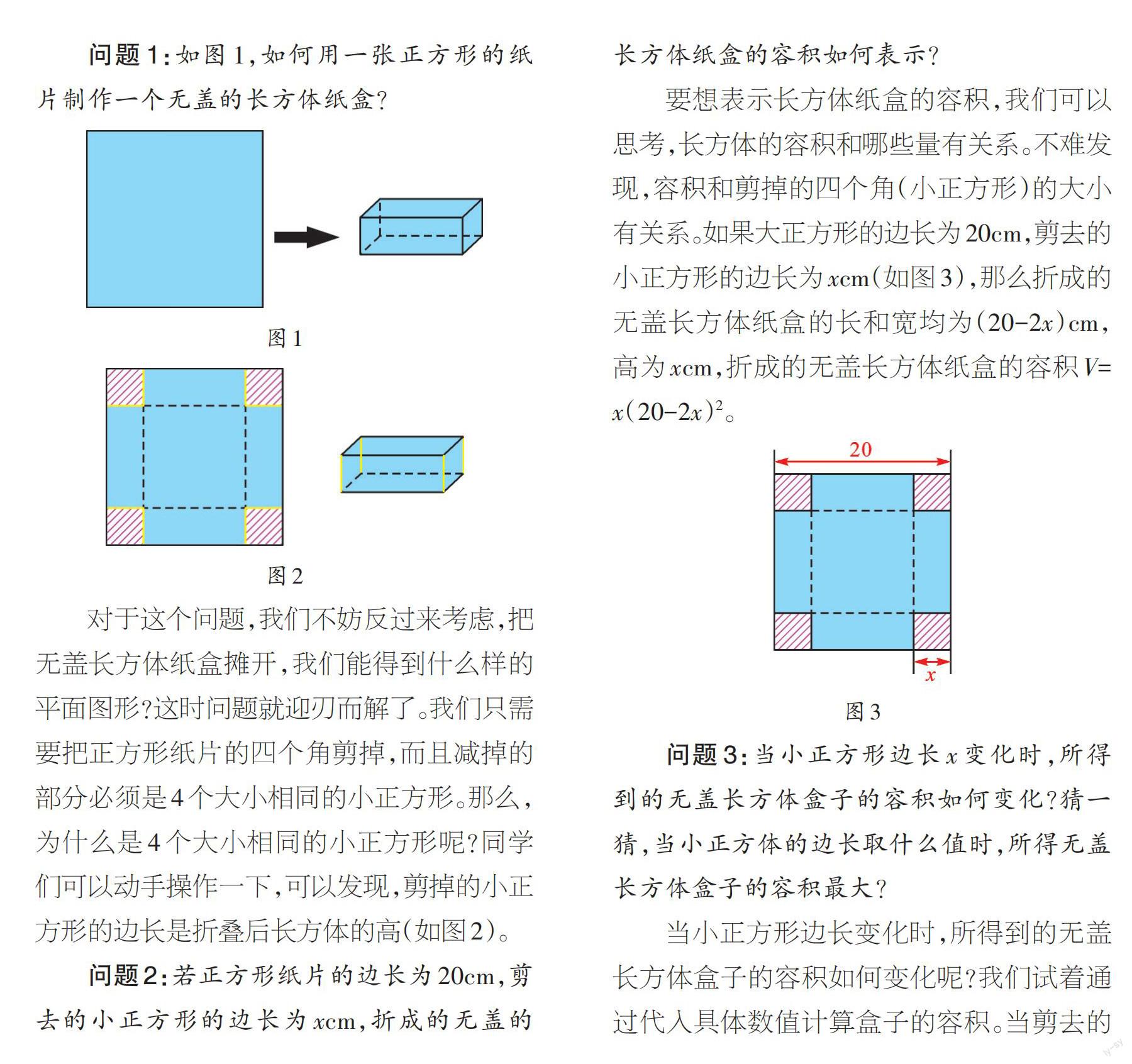
问题1：如图1，如何用一张正方形的纸片制作一个无盖的长方体纸盒？

对于这个问题，我们不妨反过来考虑，把无盖长方体纸盒摊开，我们能得到什么样的平面图形？这时问题就迎刃而解了。我们只需要把正方形纸片的四个角剪掉，而且减掉的部分必须是4个大小相同的小正方形。那么，为什么是4个大小相同的小正方形呢？同学们可以动手操作一下，可以发现，剪掉的小正方形的边长是折叠后长方体的高（如图2）。

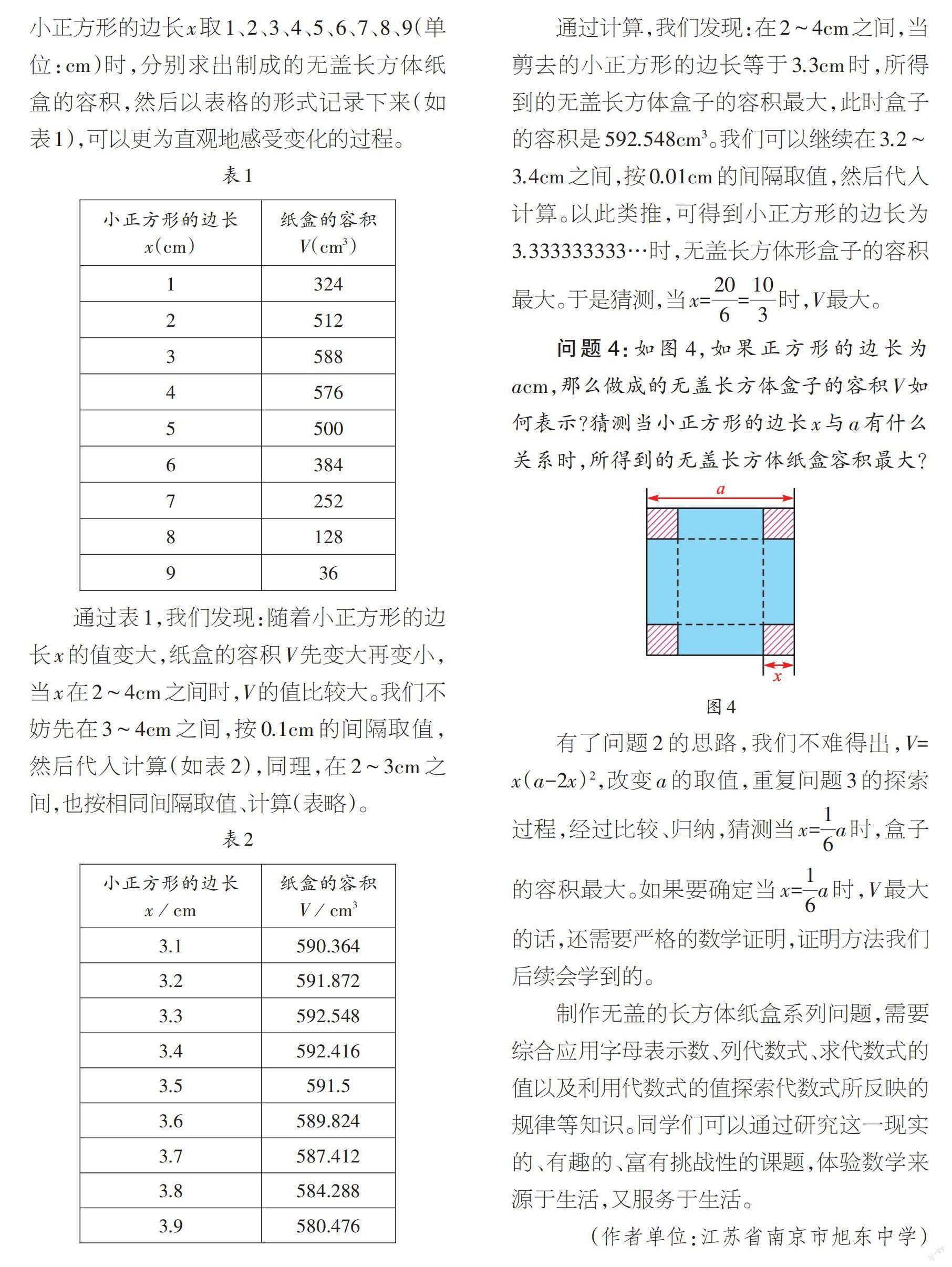
问题2：若正方形纸片的边长为20cm，剪去的小正方形的边长为xcm，折成的无盖的长方体纸盒的容积如何表示？

要想表示长方体纸盒的容积，我们可以思考，长方体的容积和哪些量有关系。不难发现，容积和剪掉的四个角（小正方形）的大小有关系。如果大正方形的边长为20cm，剪去的小正方形的边长为xcm（如图3），那么折成的无盖长方体纸盒的长和宽均为（20-2x）cm，高为xcm，折成的无盖长方体纸盒的容积V=x（20-2x）2。

问题3：当小正方形边长x变化时，所得到的无盖长方体盒子的容积如何变化？猜一猜，当小正方体的边长取什么值时，所得无盖长方体盒子的容积最大？

当小正方形边长变化时，所得到的无盖长方体盒子的容积如何变化呢？我们试着通过代入具体数值计算盒子的容积。当剪去的小正方形的边长x取1、2、3、4、5、6、7、8、9（单位：cm）时，分别求出制成的无盖长方体纸盒的容积，然后以表格的形式记录下来（如表1），可以更为直观地感受变化的过程。

通过表1，我们发现：随着小正方形的边长x的值变大，纸盒的容积V先变大再变小，当x在2～4cm之间时，V的值比较大。我们不妨先在3～4cm之间，按0.1cm的间隔取值，然后代入计算（如表2），同理，在2～3cm之间，也按相同间隔取值、计算（表略）。

通过计算，我们发现：在2～4cm之间，当剪去的小正方形的边长等于3.3cm时，所得到的无盖长方体盒子的容积最大，此时盒子的容积是592.548cm3。我们可以继续在3.2～3.4cm之间，按0.01cm的间隔取值，然后代入计算。以此类推，可得到小正方形的邊长为3.333333333…时，无盖长方体形盒子的容积最大。于是猜测，当x=[206]=[103]时，V最大。

问题4：如图4，如果正方形的边长为acm，那么做成的无盖长方体盒子的容积V如何表示？猜测当小正方形的边长x与a有什么关系时，所得到的无盖长方体纸盒容积最大？

有了问题2的思路，我们不难得出，V=x（a-2x）2，改变a的取值，重复问题3的探索过程，经过比较、归纳，猜测当x=[16]a时，盒子的容积最大。如果要确定当x=[16]a时，V最大的话，还需要严格的数学证明，证明方法我们后续会学到的。

制作无盖的长方体纸盒系列问题，需要综合应用字母表示数、列代数式、求代数式的值以及利用代数式的值探索代数式所反映的规律等知识。同学们可以通过研究这一现实的、有趣的、富有挑战性的课题，体验数学来源于生活，又服务于生活。

（作者单位：江苏省南京市旭东中学）