基于驱动性问题的小学数学教学实践

侯桂娜

【摘 要】问题是数学的心脏，好问题能激发学生学习的需求和内在动机。如果问题的质量不高，难以使学生的思考与交流真正发生。文章以“乘法的初步认识”教学为例，对教材进行解读，明确教学目标，精准把握学生的学习起点，通过设计低门槛、引导支持性、开放性的驱动性问题，有效激活学生思维，促进学生有效学习。

【关键词】驱动性问题；乘法；教材解读；学生起点

问题是数学的心脏，好问题能激发学生学习的需求和内在动机。但是当前课堂提问存在着简单碎问、随意追问或满堂问的现象，教师提出的问题大多是封闭性、唯一性的问题，答案常常是以对或错来评判。这样的封闭性问题不利于学生批判性思维、创新性思维的培养。驱动性问题是基于对教材的解读和学生起点的把握设计的具有思考性、探究性和开放性等特点的问题。学生能在驱动性问题的带动下进行思考探究、小组合作、交流碰撞，从而对数学本质的理解更全面、更客观。那么，如何在小学数学中设计驱动性问题，有效地提升课堂品质，发展学生的数学学科核心素养？笔者以人教版数学二年级上册“乘法的初步认识”一课为例，结合教学实践进行探究。

一、教前思考

（一）驱动性问题设计的路径

驱动性问题设计指向的是數学本质，也是对教材的深入解读，教学目标的精确定位，教学起点和重难点的精准把握。教师所设计的问题要具有思考性、探究性和开放性，使不同水平的学生均能调用已有的知识和经验进行思考和探究。

如对于“乘法的初步认识”一课，学生已经理解了加法的意义，具备同数连加的经验。教材分为两个层次：一是通过具体的情境列出同数连加的算式，进而介绍乘法的运算，认识乘法运算的意义，初步感受乘法运算的简洁性；二是通过情境的抽象，概括地用“几个几”的方式表达同数连加的算式，沟通加法算式与乘法算式的意义，理解乘法算式意义的本质。基于对教材的解读，本节课的教学目标为：（1）在具体的情境中理解乘法运算的意义，认识乘号，会读、写乘法算式；（2）理解求几个相同加数的和与乘法的关系，感受用乘法表示同数连加的简洁性；（3）培养学生善于倾听、乐于表达的数学学习习惯，提升学生的数学学习力。

要达到本节课的教学目标，设计问题的路径可以从以下两点考虑：一是提供同数连加的问题情境，认识乘法的意义；二是以问题驱动学生理解乘法与加法的关系。

（二）驱动性问题设计的突破口

美国数学家波利亚指出，教师应当把自己放在儿童的位置上，努力去理解儿童心里正在想什么，然后提出一个问题或者一个步骤，重要的是这些都是儿童自己想到的［1］。因此，驱动性问题设计的突破口之一就是精准把握学生的学习起点。对于“乘法的初步认识”一课，为了精准把握学生的学习起点，了解学生课前对乘法意义理解的程度，明晰学生所处的水平、学习的障碍点，笔者对本班46名学生进行了前测。

前测题 图1中一共有（  ）个。你是怎样想的，把你的想法写下来。

笔者通过整理、分析全班46名学生完成的前测题，并采用SOLO分类理论对学生的学习表现进行水平分析，将学生对乘法运算含义理解的不同水平由低到高划分为4个层次（见表1）。

由表1可以看出，处在水平2的学生居多，约占全班的73.9%，他们能基于情境理解同数连加的结构，但还不认识乘法；约有17.4%的学生虽然认识乘法，但还不是真正意义上的理解，无法理解乘法与加法的关系；而达到水平4的学生仅约占6.5%。

问题驱动式教学倡导基于学生真实的问题来展开教学，这样更能够凸显问题的驱动性，更能够基于儿童的数学现实展开教学［2］。基于对学生起点的把握，要使不同水平的学生能在已有的水平上都有所提升，关键在于让学生认识并理解几个相同加数的和与乘法的关系。因此，教师设计驱动性问题需要考虑几点：一是设计低门槛问题，使不同水平的学生都能融入课堂，进行思考；二是设计引导支持性问题，激发不同水平的学生进行交流、互动，使学生在交流碰撞中初步理解乘法的意义；三是设计开放性问题，使学生能从不同的角度思考，主动沟通同数连加与乘法意义的关系，建构乘法的意义模型。

二、教学实践

（一）设计低门槛问题，使学生融入课堂

所谓低门槛问题，指的是问题的起点较低，每个学生都能基于自己的起点，想办法来解决的问题。

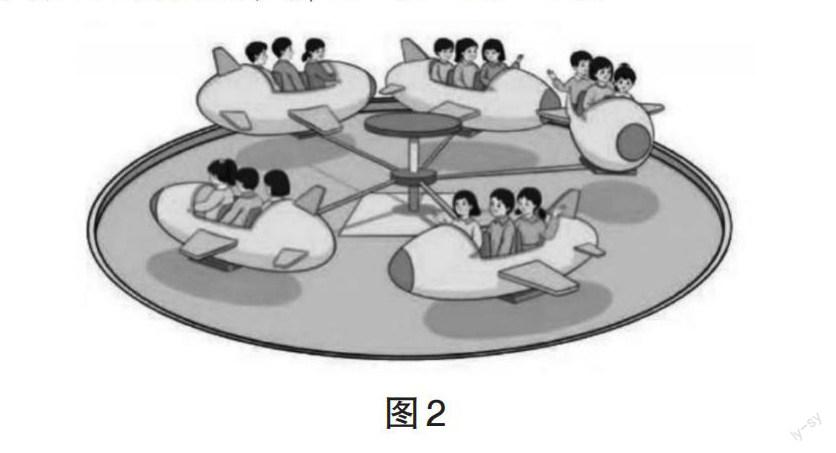
问题1 如图2，小飞机里一共有多少人？你能用自己的办法来解决吗？试一试。

生1：3+3+3+3+3=15。

生2：6+6+3=15。

生3：3×5=15。

……

通过低门槛问题，有效地驱动了不同水平的学生参与课堂的思考，如水平2的学生用同数连加的方法来解决，水平3、水平4的学生用乘法来计算，只是水平3的学生虽然能用乘法计算，但还不能像水平4的学生那样理解乘法与加法的关系。通过设置这样的低门槛问题，使不同水平的学生都能基于自己的起点，运用已有经验或方法解决问题，为接下来的交流思辨，理解乘法的意义做好铺垫。

（二）设计引导支持性问题，激发学生的交流互动

建构主义理论指出，学习过程同时包含两方面的建构，一方面是对新信息的意义的建构，另一方面是对原有经验的改造和重组［1］。当学生基于自身的起点，用原有经验解决问题后，教师需要通过设计引导支持性问题，激发学生的认知冲突，点燃学生的思维火花。

问题2 在问题1中，同学们想到了多种方法，哪些方法是我们之前学过的？说说你的想法。

生1：前面两个加法都是我们之前学过的。

生2：3+3+3+3+3=15指的是每架小飞机都有3个人，因为有5架，所以要把5个3加起来。

师：很棒，能够图与式一一对应。

问题3 哪些方法看不懂？说一说你的疑问。

生1：6+6+3=15有点看不懂，6是哪里来的呢？

生2：6就是把2个3合在一起。

生3：3×5=15这个算式表示什么意思？

生4：3×5=15与加法算式3+3+3+3+3=15有关系吗？

……

师：同学们都很善于思考，提出了很多有价值的问题，接下来将由四人一组，一起合作探究同学3、同学4提出的问题。

（学生进行热烈的小组讨论。）

生5：（指着图2）3×5=15中的3指的是每组都有3人，5表示有5个3。

生6：原来3×5也表示5个3合起来。那3×5与加法算式3+3+3+3+3=15有关系吗？

生7：（边指边说）有关系的，乘法算式里的5指的是加法算式中3的个数有5个。

首先，教师通过问题2引导学生学会倾听、读懂他人的想法，对不同的想法做进一步解释说明，为乘法意义的理解做好铺垫。然后，教师通过问题3激活不同水平的学生对乘法意义理解的生长点和困惑点。最后，教师将学生的困惑点生成引导支持性问题，把个别学生的思考引向全班，使不同水平的学生在互相质疑、补充、交流碰撞中，实现课堂的有效对话，理解乘法与同数连加的关系和几个几相加的道理，使學生努力向水平4发展。

（三）设计开放性问题，激活学生的思维

为了激活学生的思维，使学生的学习不只是依葫芦画瓢，教师变换情境，设计开放性问题，让学生在进一步理解乘法意义的基础上进行应用和创造。

问题4 图3中一共有多少只熊猫？大家能想办法解决吗？（圈一圈，说一说，写一写。）

学生通过独立尝试，自主圈一圈，呈现出不同的想法。

生1：2+2+2+2+2+2=12，2×6=12。

生2：6+6=12，2×6=12。

生3：3+3+3+3=12，3×4=12。

生4：4+4+4=12。

生5：6×6。

……

师：同学们都很善于观察和思考，懂得从不同的角度圈一圈，使每组熊猫的数量相同，并都想办法解决了问题。你能看明白他们的想法吗？有疑问或补充的吗？

生6：同学5用6×6是怎么想的？跟我们算的结果不一样。

生5：第一行有6只熊猫，第二行也有6只熊猫，所以是6×6。

生7：这里有6个6吗？你数给我们看看。

生5：（边圈边数）这里有1个6，2个6。噢，原来两行熊猫合在一起是2个6，要写成2×6才对。

师：同学们不仅能提出问题，还能自己说明理由，更了不起的是能自我反思并改正。通过刚才的交流学习，你对乘法有什么新的认识吗？

生8：只要每一份圈得同样多就可以用乘法计算。

生9：我发现用乘法来表示几个几相加比较简便。

……

师：你能摆一幅可以用乘法计算的图吗？

在开放的问题情境中，不同水平的学生从不同角度去观察、获取信息，通过圈一圈，展示自己的想法；说一说，读懂他人的想法。学生进一步交流思辨不同的想法，理解乘法的意义，感知同数连加的算式改写成乘法算式的意义本质，不断地建构起乘法的意义模型。最后，学生在理解乘法意义的基础上用磁铁玩具创造出乘法计算的图，使乘法从课本延伸到课外。

三、教后反思

在本节课学习后，笔者对全班46名学生进行了再次评价，以了解学生对乘法意义理解水平的发展情况。通过后测发现，没有水平1和水平2的学生，水平3的有5人，水平4的有41人，学生总体的水平都有大幅度提升。之所以取得较好的教学效果，得益于驱动性问题的设计。

（一）通过驱动性问题，促进学生思考

驱动性问题是以学为核心，关注学生学的思考性，强调的是问题的“质”，能够给予学生更多的空间进行独立思考与主动探究，使学生爱思考、爱探究。本节课设计了很多驱动性问题，如“小飞机里一共有多少人？”“你能摆一幅可以用乘法计算的图吗？”等。这些问题都具有开放性和思考度，不同水平的学生都能基于自己的起点进行思考，激发了学生学习数学的兴趣，培养了学生的自信心。

（二）通过驱动性问题，促进学生互动

驱动性问题可以激活学生的思维，同时让课堂提问得到更多有价值的信息，增强师生之间、生生之间的互动。如在解决“小飞机里一共有多少人？”问题时，不同水平的学生有不同的思考，有同数连加的，也有简便加的，还有用乘法计算的。教师通过“哪些方法看不懂，说一说你的疑问。”的驱动性问题，激活了学生的思维火花。学生互相质疑、提问，在交流互动的过程中，不断建构同数连加与乘法的联系，理解乘法运算的意义。

（三）通过驱动性问题，促进学生反思

教师通过营造轻松的课堂氛围，在问题的驱动下，使学生对学习内容的认识经历“原来我是怎样想、怎样做—还可以这样想、这样做—现在我是这样想、这样做”的过程，思维从平衡到失衡，再形成新的平衡，从而建构起对乘法意义的理解。如在解决“一共有多少只熊猫？”时，学生敢于从不同的角度思考。当学生的观点受到质疑时，学生需要为自己的观点辩护、说理，进一步解释自己的想法；当理由不够充分时，学生通过反思原来的观点，重构自己的理解。如学生用6×6来计算熊猫的数量受到质疑时，学生通过借助图来说理，数出有几个6，发现原来的想法不正确，进而反思并做出调整。由此，学生在质疑说理的过程中不断反思，深化对乘法意义的理解。

因此，通过设计不同程度的驱动性问题，能有效激发学生思考，激活学生的生长点和困惑点，让不同水平的学生进行多向的交流互动，有理有据地进行数学说理，建构对数学知识意义的理解，使课堂的学习真正发生，使学生的数学关键能力和学科核心素养得到提升与发展。

参考文献：

［1］赵国防.指向学科关键能力的“问题串”教学［J］.江苏教育研究，2021（19）：102-106.

［2］储冬生.问题驱动式教学：从模式到实践：兼评两则《多边形的内角和》教学案例［J］.教育视界，2022（11）：51-52.

（责任编辑：罗小荧）