基于修正高斯烟团模型的SO2瞬时排放扩散研究
王竟成,王津梅,李兆辰,杨雨岚,李泽华,杨 祎
(1.中国兵器工业第五九研究所装备环境工程研究中心,重庆 400039;2.中国地质大学(武汉)数学与物理学院,湖北 武汉 430074)
工业装备是工业生产或运作的基础,工业装备服役期间,其设备完好与否决定了其使用寿命的长短,而工业装备的腐蚀控制是设备完好的重要保证[1]。工业装备被腐蚀的主要原因之一是酸雨[2],酸雨会导致工业装备起保护作用的防护层发生电化学腐蚀,使防护层的防护时间大大缩短,因此有效减少工业装备腐蚀的方法之一就是防止酸雨的形成。
二氧化硫(SO2)是主要的大气污染物之一,在一定的湿润条件下,大气中的SO2会与其他污染物质形成酸雨,使工业装备的防护层发生电化学腐蚀[3],因此治理大气中的SO2污染尤为重要。为了从源头上治理大气中的SO2污染,需要进一步建立模型来分析高架点源SO2排放对区域大气和周围环境的影响,预测大气中SO2的浓度分布,以便于对一定区域内大气中SO2浓度进行监测。
常见的大气扩散模型有高斯模型、拉格朗日模型和欧拉模型。其中,高斯模型一般应用于固定点源污染物浓度扩散的模拟研究。大量试验研究表明,对于稳定污染点源排放的污染物,其浓度分布符合正态分布,可以由湍流统计理论推导出一系列的高斯扩散模型[4]。与其他两类大气扩散模型相比,高斯模型具有以下优势:①在小尺度范围的大气扩散模拟应用中,模拟结果较为精准;②需要输入的数据较少,数据获取难度较低;③计算量较小,可计算性强;④模型构架清晰简洁,能够根据点源的地理信息数据、扩散时间段的气象数据,对模型和参数进行调整和修正。另外,高斯模型为体系成熟最早、适用范围最广的模型,但该模型未考虑大气扩散中的化学变化因素[5]。
高斯模型中的高斯烟羽模型[6-7]和高斯烟团模型[8]在稳定点源排放的污染物扩散模拟中,都有精度较高的模拟结果,两者都是基于湍流统计理论推导得到的[9]。在稳定点源排放的污染物扩散模拟研究方面,王淑莹等[10]利用高斯烟羽模型模拟了某热电厂对邻近区域监测站点空气质量的影响;陈坤等[11]为了预测含硫天然气泄漏后危险气体的扩散浓度和地形对气体扩散的影响,以高斯烟羽模型为基础,对含硫天然气在不同地形条件下连续泄漏的模型进行了研究,得到了相应的下风向气体扩散浓度及其危害距离;王洪德等[12]利用高斯烟团模型对天然气瞬时泄漏的气体扩散规律进行了数值模拟仿真,并基于数值模拟仿真分析结果,提出了天然气泄漏后的应急疏散和救护措施;李冰晶等[13]利用高斯烟团模型对某石化项目的大气环境影响进行了风险识别与分析,对脱硫装置发生特大灾害性事故状态下的硫化氢泄漏进行了数值模拟,最后确定了其危害距离。
目前,国内外研究更多关注于稳定点源连续排放的污染物扩散情况,而针对瞬时排放的污染物扩散研究较少[14-15]。在小风静风情况下,高斯烟羽模型由于忽略了烟气沿风方向的水平扩散,使其模拟效果不佳,而高斯烟团模型考虑了沿风方向的大气扩散对污染物浓度分布的影响,使其对小风静风情况下污染物的浓度预测精度较高。为此,本文针对排放时间与扩散时间不同的情况对高斯烟团模型进行了改进,提出了修正的高斯烟团模型,对小风静风条件下高架稳定污染点源瞬时排放SO2的浓度扩散分布情况进行了研究。具体思路为:在高斯烟团模型的基础上,将高架稳定点源的SO2排放看作是有限个烟团的叠加,并针对烟团扩散时间大于排放时间的情况对高斯烟团模型进行了修正,即先计算扩散时间所有SO2浓度贡献值的叠加,然后减去由扩散时间与排放时间的时间差所产生的多计算的SO2浓度贡献值,由此给出了基于高斯烟团模型的稳定点源瞬时排放的大气污染扩散模型,模拟SO2稳定连续排放一段时间后不再排放的情况,对近污染源地区大气中SO2的浓度进行实时预测。
1 基于高斯烟团模型的稳定点源连续排放
1.1 高斯烟团模型坐标系的建立及模型假设
高斯烟团模型的坐标系建立如下:以污染点源在地表面的投影作为坐标原点o,模拟时间段的主风向作为x轴正向,地表面上主风向的法向作为y轴,z轴垂直于xy平面向上延伸(见图1)。图中,H(m)为点源有效高度,包括烟囱高度h(m)和抬升高度Δh(m)。该坐标系适用于高斯烟团模型以及修正的高斯烟团模型。

图1 高斯烟团模型坐标系
高斯烟团模型主要用于研究小风静风条件下(地面平均风速u<1.5 m/s)大气污染物扩散的规律,模型假设如下:
(1) 风速大小恒定且风向沿着x轴方向,y和z方向的风速为0;
(2) 大气污染物的浓度在水平和垂直方向上服从正态分布;
(3) 流场是均匀的;
(4) 大气污染物在输送扩散过程中质量守恒,不发生沉降和化学反应;
(5) 污染源的源强排放均匀、连续、稳定。
1.2 稳定点源连续排放的高斯烟团模型
1.2.1 单个烟团对空间一点处SO2浓度分布计算模型
高斯烟团模型是根据湍流扩散理论和统计理论等来推导描述的,湍流扩散的微分方程如下:
(1)
式中:C为空间中任意一点(x,y,z)处的污染物浓度(mg/m3);t为污染物扩散时间(s);u、v、w分别为x、y、z方向的风速(m/s);Kx、Ky、Kz分别为x、y、z方向的湍流扩散系数(m2/s)[16]。
首先考虑一维简化情况,有:
(2)
在无风情况即u=0时,公式(2)可简化为
(3)
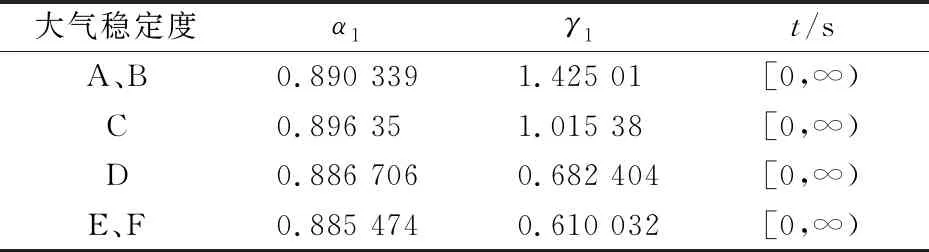
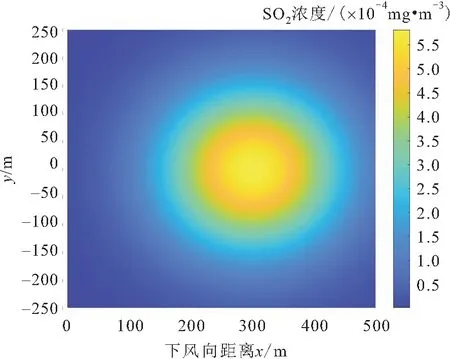
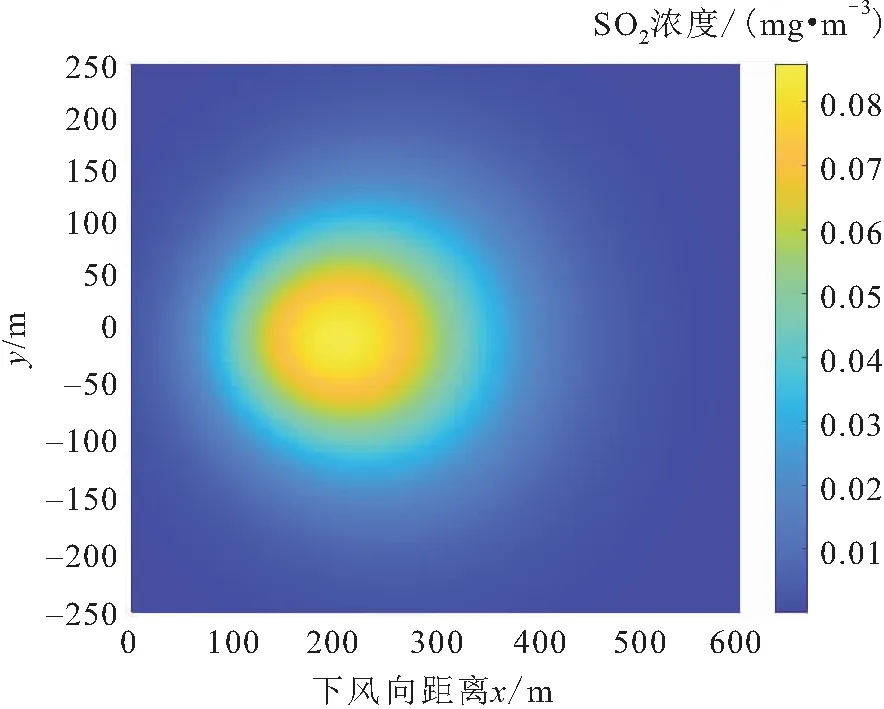
初始条件:t=0时,x=0处,C→∞;t=0时,x≠0处,C→0。边界条件:t→∞时,C→0(-∞ (4) 式中:Q为源强(mg/s)。 推广到三维,可以得到三维空间下大气污染物源强为Q的瞬间点源的大气污染物浓度分布为 (5) 式中:σx、σy和σz分别代表小风静风条件下水平和垂直方向的大气扩散参数(m),其与大气稳定度和烟团扩散时间有关。 由于小风静风条件下测量扩散参数的技术要求较高,且观测试验以及取得的资料较少,有时不得不采用σx=σy的粗略近似方法。实际中运用比较广泛的是Turner根据美国圣路易城大气扩散试验总结出的微风条件下的大气扩散参数,见表1和表2[17]。表1和表2中,γ1、γ2分别表示小风静风条件下水平和垂直方向大气扩散参数的回归系数;α1、α2分别表示小风静风条件下水平和垂直方向大气扩散参数的回归指数;t表示污染物扩散时间(s)。则大气扩散参数σx、σy、σz可表示如下: 表1 小风静风条件下水平方向的大气扩散参数 表2 小风静风条件下垂直方向的大气扩散参数 σx=σy=γ1tα1 (6) σz=γ2tα2 (7) 考虑到地面的影响,原点取在污染源在地面的垂直投影点上(见图1),有效高度为H,同时考虑到风速u的影响,可得小风静风条件下单个烟团扩散的SO2浓度分布计算模型为 (8) 本文模拟了点源在源强Q为8 000 mg/s、有效高度H为81.048 2 m、风速u为1 m/s、大气稳定度等级为D时,仅排放单个烟团的SO2扩散情况。设定扩散时间t1=300 s,模拟得到z=0 m时单个烟团扩散300 s时xy平面上SO2浓度分布和y=0 m时单个烟团扩散300 s时xz平面上SO2浓度分布的仿真结果,见图2、图3。 图2 z=0 m时单个烟团扩散300 s时xy平面上的SO2浓度分布 图3 y=0 m时单个烟团扩散300 s时xz平面上的SO2浓度分布 由图2、图3可知:在xy平面上,SO2浓度以x=ut=300 m、y=0 m为对称轴分布,SO2浓度峰值出现在x=300 m、y=0 m处;在xz平面上,SO2浓度以x=ut=300 m为对称轴分布,由于地面的影响,会在z方向产生SO2浓度的累积。 1.2.2 稳定点源连续排放对空间一点处SO2浓度分布计算模型 将烟团扩散时间t1内每个瞬间点源叠加,得到小风静风条件下高架稳定点源连续排放的高斯烟团扩散浓度分布模型为 (9) 本文在高斯烟团模型的基础上,研究高架稳定点源排放污染物一段时间后停止排放的情况 (即稳定点源瞬时排放)下,在近污染源地区大气中SO2的浓度分布计算模型。因此,需要对上述高架稳定点源连续排放的高斯烟团扩散模型进行修正。考虑到烟团排放时间和扩散时间的不同,将分为两种情况来进行研究。 (1) 烟团扩散时间t1小于或等于排放时间t2的情况。当烟团扩散时间小于或等于排放时间时,可以直接利用稳定点源连续排放的高斯烟团扩散模型[即公式(9)]来预测近污染源地区大气中SO2的浓度。由于预测时刻排放还在进行,因此在点源处会有SO2浓度最大值,且点源附近的SO2浓度值会明显大于与点源相距较远处的SO2浓度。 (2) 烟团扩散时间t1大于排放时间t2的情况。由于扩散时间大于排放时间,在排放时刻到扩散时刻之间的这段时间内,点源已不再排放SO2,因此不能使用稳定点源连续排放的高斯烟团扩散模型[即公式(9)]来预测近污染源地区大气中SO2的浓度,为此本文对稳定点源连续排放的高斯烟团扩散模型进行了修正。假设烟团扩散时间为t1、排放时间为t2,两者时间差为t3=t1-t2,若为稳定点源连续排放,则公式(9)的积分上、下限为t1、0,即从0时刻到t1时刻的所有烟团SO2浓度贡献值的叠加,但此时t2 (10) 综上,可以得到修正后的高斯烟团模型为 其中,f(t)的表达式为 采用修正的高斯烟团模型预测近污染源地区大气中SO2浓度的流程图,见图4。 图4 修正的高斯烟团模型实现流程图 修正的高斯烟团模型实现上述流程的具体步骤如下: (1) 输入数据:污染源源强Q、大气稳定度等级、点源有效高度H,预测位置坐标(x、y、z)、x轴方向风速u、烟团扩散时间t1、烟团排放时间t2。 (2) 比较烟团扩散时间t1和烟团排放时间t2的大小,如果t1≤t2,基于修正的高斯烟团模型,可以利用公式(11-1)求解污染物SO2浓度C。 (3) 如果烟团扩散时间t1>烟团排放时间t2,基于修正的高斯烟团模型,可以利用公式(11-2)求解污染物SO2浓度C。 (4) 输出结果:所输入坐标区域对应的污染物SO2浓度值C,模拟得到污染物浓度分布图。 本文模拟点源在源强Q为8 000 mg/s、有效高度H为81.048 2 m、风速u为1 m/s、大气稳定度等级为D时瞬时排放的SO2扩散情况。 设定t1=t2=300 s,z=0 m时xy平面上SO2浓度分布和y=0 m时xz平面上SO2浓度分布的仿真模拟结果,见图5和图6。 图5 t1=t2=300 s、z=0 m时xy平面上SO2浓度分布的模拟结果 图6 t1=t2=300 s、y=0 m时xz平面上SO2浓度分布的模拟结果 由图5和图6可知:z=0 m时xy平面上SO2浓度关于y=0 m对称,且在沿风向方向的SO2扩散程度更大;y=0 m时xz平面上SO2浓度在点源有效高度处取得峰值,且SO2浓度随着与污染源距离的增大而减小。 3.2.1t1=600 s、t2=300 s时稳定点源瞬时排放过程中SO2浓度变化监测 设定t1=600 s、t2=300 s,z=0 m时xy平面上的SO2浓度分布和y=0 m时xz平面上SO2浓度分布的仿真模拟结果,见图7和图8。 图7 t1=600 s、t2=300 s、z=0 m时xy平面上SO2浓度分布的模拟结果 图8 t1=600 s、t2=300 s、y=0 m时xz平面上SO2浓度分布的模拟结果 由图7和图8可知:在t1=600 s、t2=300 s,z=0 m时xy平面上SO2浓度分布在沿风向方向的扩散程度更大,整体呈椭圆形状扩散;在y=0 m时xz平面上SO2浓度分布在沿风向方向的扩散程度较大,且由于地面的影响,在近地面z方向上有SO2浓度的累积。 3.2.2t1=7 200 s、t2=3 600 s时稳定点源瞬时排放过程中SO2浓度变化监测 设定t1=7 200 s、t2=3 600 s,z=0 m时xy平面上SO2浓度分布和y=0 m时xz平面上SO2浓度分布的仿真模拟结果,见图9和图10。 图9 t1=7 200 s、t2=3 600 s、z=0 m时xy平面上SO2浓度分布的模拟结果 图10 t1=7 200 s、t2=3 600 s、y=0 m时xz平面上SO2浓度分布的模拟结果 由图9和图10可知:z=0 m时在xy平面上,经过长时间的扩散,SO2烟团的浓度分布会集中在距离点源较远的位置,且SO2浓度覆盖的范围更广,同时在沿风向方向上SO2有更大的扩散程度;y=0 m时在xz平面上,经过长时间的扩散,SO2浓度在z方向上覆盖的范围较广,且由于地面的影响SO2浓度峰值会出现在近地面处。 经典的高斯烟团模型在模拟小风静风条件下稳定污染源的污染物扩散问题上,具有模型简单、近污染源区域模拟效果好等优点,但该模型只能模拟稳定污染点源连续排放的情况。针对SO2瞬时排放(排放一段时间后不再排放)的问题,本文建模为排放时间内有限个SO2烟团的叠加,并对经典的高斯烟团模型进行了修正,建立了适用于稳定污染点源瞬时排放的修正高斯烟团模型,实现了对近污染源地区大气中SO2浓度的实时预测。仿真模拟实验结果表明,本文建立的修正高斯烟团模型能较好地估算稳定点源瞬时排放情况下SO2浓度分布,证明该模型对于大气中SO2污染浓度估算具有实际意义。本文提出的修正高斯烟团模型及其构建思路也能为其他污染物或不同污染源的污染物扩散分布研究提供一定的参考,为有效减少大气污染提供有力的理论支撑。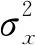


2 基于修正的高斯烟团模型的稳定点源瞬时排放
2.1 修正的高斯烟团模型
2.2 修正的高斯烟团模型实现流程

3 实例仿真模拟
3.1 扩散时间小于或等于排放时间时稳定点源瞬时排放过程中SO2浓度变化监测
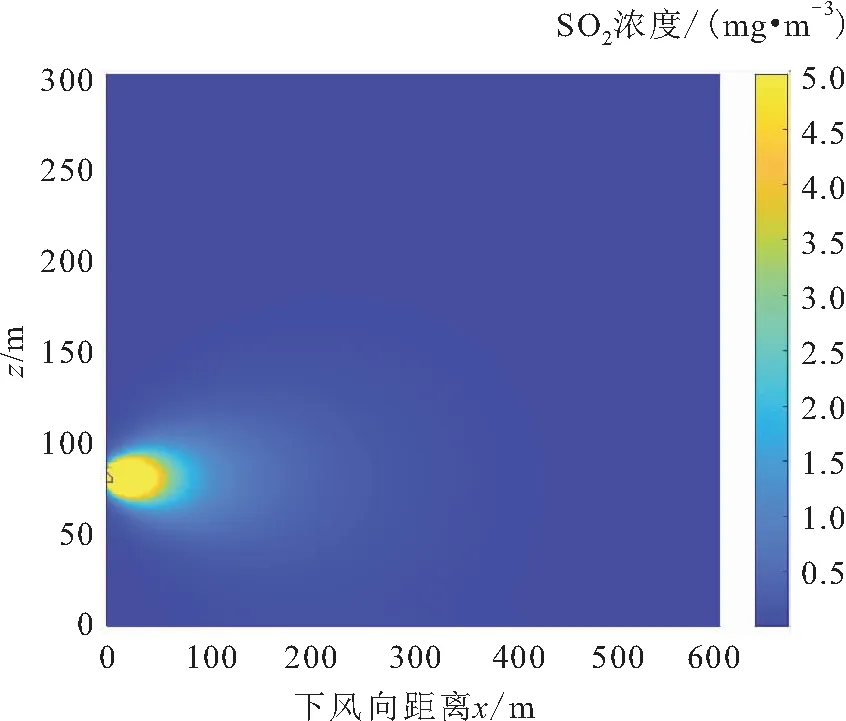
3.2 扩散时间大于排放时间时稳定点源瞬时排放过程中SO2浓度变化监测



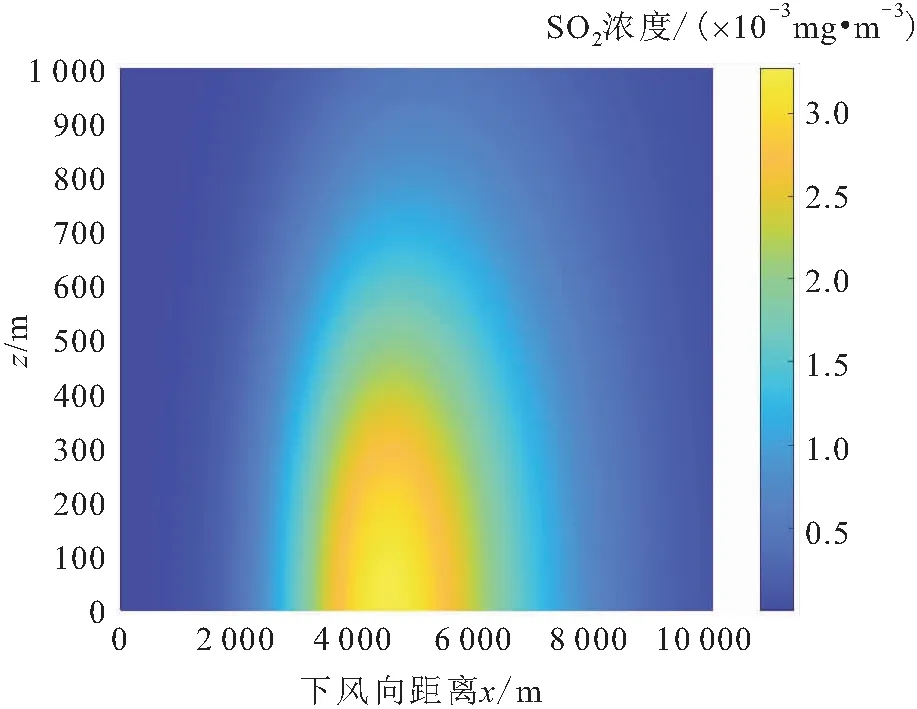
4 结 论

