悬挂式止水帷幕条件下基坑涌水量计算研究

王 浩，刘艳敏,，赵 渊，任兴伟*

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.武汉市勘察设计有限公司，湖北 武汉 430022)

随着城市地下空间的利用率越来越高，对深基坑工程的降水支护设计要求也越来越严格，基坑止水帷幕结合坑内井点降水的模式已被广泛应用，以有效控制降水诱发的地面沉降[1]。现行的《建筑基坑支护技术规程》(JGJ 120—2012)中只给出了开放式场地下基坑涌水量的计算公式[2]，即将群井按大井简化，给出了潜水和承压水下完整井与非完整井的涌水量计算公式。但实际基坑工程中，止水帷幕对基坑渗流场的影响是极大的，实际基坑涌水量比规程公式计算结果小，若不考虑止水帷幕引起的基坑降水有利因素，将会导致基坑降水施工设计与现场实际需求差异较大，采用的基坑降水施工方案并不经济、合理。因此，考虑止水帷幕影响下基坑涌水量研究具有重要的理论意义和工程应用价值。

目前已有大量学者针对基坑止水帷幕和地下水渗流场进行了研究，但业内对悬挂式止水帷幕减压降水条件下基坑涌水量预测尚无统一的估算方法，人们大多采用工程经验类比法或数值模拟软件来预测基坑涌水量。如：李瑛等[3]将基坑按面积相等等效为井壁进水的大直径承压水非完整井，并令流入井内的水量等于止水帷幕内坑底承压水含水层内的竖直向渗流量，以此建立基坑内减压抽水量与基坑外承压水头降深的关系式；曹洪等[4]提出了简便可行的渗流场分层方法，并以此为基础对计算简便、精度较高的沙金煊公式进行了改进与完善，得到了适用于滤管顶、底均不在含水层层面的承压不完整井渗流量的近似计算方法；吕斌泉等[5]针对落底式止水帷幕渗漏的不确定性，结合映射原理，推导出含水层等效渗透系数计算公式，提出采用涌漏系数法来评价落底式止水帷幕隔渗效果和计算基坑涌水量；秦志忠[6]分别建立了承压含水层完整井、非完整井和含悬挂式隔水帷幕的基坑涌水量有限元模型，分析结果表明承压含水层完整井基坑涌水量的理论计算值与有限元模拟值一致，而承压含水层非完整井基坑涌水量的理论计算值较有限元模拟值偏小，且当含水层厚度超过滤管长度3倍时其理论计算结果与有限元模拟值相比已出现较大的误差；杨建民等[7]将基坑涌水量分为基坑内储水量和基坑底及基坑外向基坑内的渗流量，并提出了各自的计算公式，从而给出了一种深基坑降水工程的涌水量计算方法；马陨等[8]以长江Ⅰ级阶地复杂条件下的深基坑为例，提出在弱透水层的潜水和承压含水层中采用在支护桩之间施打高压旋喷桩形成竖向隔水帷幕，在强透水层的承压含水层中采用井管降水的方法来控制基坑涌水量，但降水井的深度要适当；石中平[9]通过对现行规范和相关文献中基坑涌水量计算公式的对比分析，阐述了基坑涌水量计算公式存在的一些问题，并根据地下水渗流理论，给出了修正后的基坑涌水量计算公式；Liu等[10]采用有限差分法分析了部分贯通止水帷幕基坑降水工程的地下水三维渗流特性，并在等效井假设下，通过量化阻塞效应，建立了标准曲线和畸变函数，从而进一步发展了地下水稳定流的经验入流预报公式；Farinha等[11]通过在拱坝坝基区域进行一系列涌水量试验和导水率分析，考虑了岩体渗透性试验结果和渗流路径穿过各排水沟的区域，给出了用于分析两个基础领域的试验数据的详细的三维(3D)数值模型；Vogel等[12]介绍了一种描述以结转蓄水为主的供水系统总体性能的近似通用方法，对自回归正态和对数正态年进水量供水的供水系统，引入了水库系统库容、产量、可靠性和恢复力之间的广义关系；Kamel等[13]通过稳定同位素和放射性同位素对加夫萨-南矿区(突尼斯西南部)的多层含水层之间的渗透性进行了研究，分析了深层承压水和浅层承压水的补给来源；Barzegar等[14]在伊朗大不里士平原进行了详细的水文地质调查并结合数值模拟方法，分析了两种不同水质含水层之间的联系与渗漏情况。

本文基于裘布依稳定承压井流理论，考虑了悬挂式止水帷幕对基坑地下水水力梯度和渗流断面的影响，对承压含水层、悬挂式止水帷幕条件下基坑涌水量进行了理论推导，并针对汉口客运中心基坑进行建模，通过设置不同工况模拟出基坑涌水量并与理论公式计算结果进行了对比分析；同时通过查阅相关基坑工程案例降水资料，将现场实测的基坑涌水量与理论公式计算结果进行了对比，用于验证考虑止水帷幕后基坑涌水量理论公式的计算结果是否具有准确性和可行性。

1 悬挂式止水帷幕条件下基坑涌水量的理论计算

目前基坑降水设计主要通过开展专项抽水试验以获得现场水文地质参数，再结合工程概况和地层条件预测出基坑涌水量来进行降水井的布置。现行的JGJ 120—2012中将群井按大井简化，给出了均质含水层承压水完整井的基坑总涌水量计算公式[见公式(1)]，其计算模型如图1所示。但均质含水层承压水非完整井基坑涌水量计算公式的适用性还有待进一步验证，由文献[6]可知大部分情况下均质含水层承压水非完整井基坑涌水量的计算结果较实际情况偏小，对于基坑工程是偏于不安全的；对于含水层厚度不大的均质含水层承压水非完整井，当滤管长度超过含水层一半时，一般用完整井基坑涌水量计算公式计算基坑涌水量，其结果对于基坑工程是偏安全的。因此，为了简化基坑涌水量计算公式，方便其在基坑工程中的应用，本文采用均质含水层承压水完整井基坑涌水量计算公式对基坑涌水量进行理论分析和推导，其计算公式如下：

图1 均质含水层承压水完整井的基坑涌水量计算模型

(1)

式中：Q为基坑涌水量(m3/d)；K为承压含水层渗透系数(m/d)；s0为基坑设计地下水水位降深(m)；r0为基坑等效半径(m)；R为基坑降水影响半径(m)；M为承压含水层厚度(m)。

由公式(1)可以看出，该计算公式没有考虑基坑降水设计中止水帷幕的存在。而止水帷幕对基坑降水渗流环境有较大的影响，主要体现在以下几个方面：①延长地下水渗流路径，减小水力梯度。在悬挂式止水帷幕存在的情况下，基坑外地下水需要绕过止水帷幕底端进入基坑内；②改变了基坑内、外地下水水位降深。基坑内、外地下水水位由连续性变为阶段性；③减小了基坑涌水量。由Darcy定律可知，止水帷幕插入含水层一定深度后，地下水渗流路径增加、渗流断面面积减小，使得基坑涌水量减小。因此，本文对悬挂式止水帷幕影响下基坑降水渗流场进行深入研究，即基于裘布依稳定承压井流理论，以大井法模型(见图1)为基础，加入悬挂式止水帷幕边界条件，推导出一种更符合基坑存在止水帷幕情况下的基坑涌水量计算公式，其计算模型如图2所示。

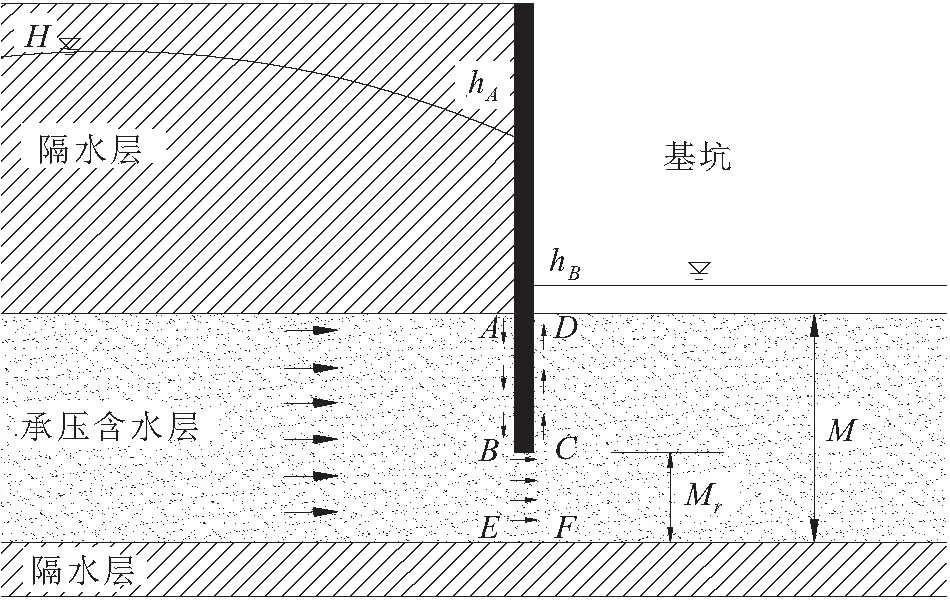
图2 悬挂式止水帷幕下基坑涌水量计算模型

图2中，假设圆形基坑半径为r0(非圆形基坑可按相等面积圆形基坑换算)(m)，悬挂式止水帷幕长(即止水帷幕插入承压含水层中的深度，也称为止水帷幕深度或落深)为L(m)，厚度为D(m)，承压含水层厚度为M(m)，基坑降水影响半径为R(m)，止水帷幕底端到隔水底板的距离为Mr(m)，基坑外承压地下水水位标高为H(m)，抽水后止水帷幕外侧地下水水位标高为hA(m)，基坑内设计地下水水位标高为hB(m)。

根据Darcy定律Q=KAi，可求得止水帷幕外侧底端的地下水径流量，即基坑的总涌水量Q(此时基坑面积A=2πr0Mr)为：

Q=2πKr0Mri

(2)

式中，i为地下水水力梯度(m)。

根据流网理论，地下水渗流路径在靠近止水帷幕底端处为A→B→C→D，在靠近隔水底板处为E→F，两处地下水的水力梯度i分别如下：

(3)

(4)

i1、i2距隔水底板距离分别为Mr、0，通过线性函数法可求出距隔水底板Mr/2处的地下水水力梯度，即存在止水帷幕下基坑外地下水进入基坑内的平均水力梯度为

(5)

将公式(5)代入公式(2)中，可得：

(6)

假设地下水渗流路径只有在无限接近止水帷幕处才沿着A→B→C→D，基坑外地下水渗流仍普遍认为是水平方向流动。根据Darcy定律和Dupuit基本假定，基坑外地下水水位降深s仍可通过公式(1)来计算，即：

(7)

设基坑设计地下水水位降深为s0，建立如下等式：

s0=H-hB=s+hA-hB

(8)

联立公式(6)、(7)和(8)，可得：

(9)

根据公式(9)，换算出基坑涌水量为

(10)

式中：Mr为承压含水层剩余厚度(m)；D为止水帷幕厚度(m)。

公式(10)即为均质承压含水层、考虑悬挂式止水帷幕影响下基坑涌水量的理论计算公式。

2 基坑涌水量理论计算公式的案例验证

为了验证本文提出的承压含水层、考虑悬挂式止水帷幕影响下基坑涌水量理论公式计算结果的准确性与可行性，利用3个基坑工程案例对比分析了本文理论公式计算值与现场实测值的差异。

本研究选取的工程案例如下：甲和乙分别为上海轨道交通11号线临港新城北站基坑工程和上海轨道交通4号线董家渡隧道基坑工程，丙为上海轨道交通10号线南京东路站Ⅲ区基坑工程，其理论公式基坑涌水量的计算参数取值主要来源于参考文献[15]、[16](见表1)。3个基坑工程案例基坑涌水量理论公式计算值与实测值的对比，见表2。

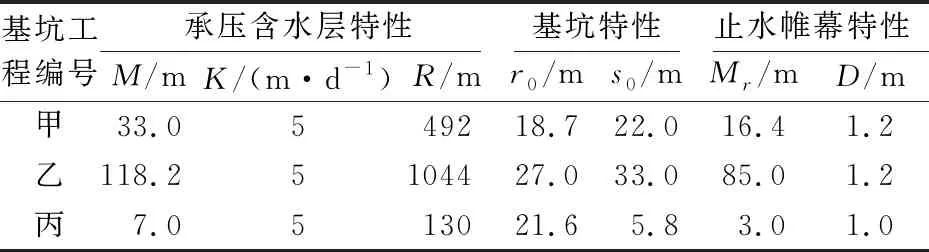
表1 3个基坑工程案例理论公式基坑涌水量的计算参数取值

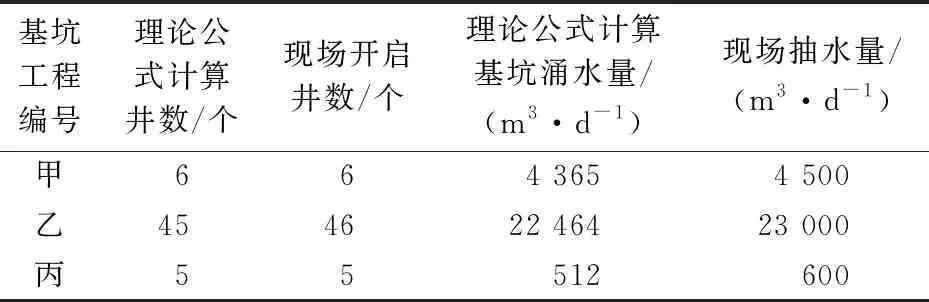
表2 3个基坑工程案例基坑涌水量理论公式计算值与实测值的对比

由表2可知，基坑涌水量理论公式计算结果与现场实测数据基本一致，证明采用基坑涌水量理论公式(10)的计算结果具有一定的准确性和可行性。但通过本文理论公式计算得到的基坑涌水量结果略小于现场实测值，这是因为理论公式的计算模型更理想化，即将止水帷幕和隔水层考虑成完全隔水，不存在渗漏的情况。因此，下一步还需要通过对具体工程实例进行数值模拟来验证理论公式的准确性。

3 工程实例应用与分析

3.1 工程概况

汉口客运中心基坑位于武汉市江汉区发展大道与后襄河北路之间，东西两侧分别为后襄河一路和后襄河二路，紧邻道路及居民楼，周边环境较复杂，其基坑平面位置如图3所示。该基坑近似矩形，长约260 m，宽约130 m，场地整平标高约为21 m，基坑开挖深度约地面以下15 m。本工程基坑采用明挖顺作法施工，基坑降水方案采用悬挂式止水帷幕结合坑内井点降水，止水帷幕深度为30 m、厚度为0.8 m。

图3 汉口客运中心基坑平面位置图

3.2 工程地质与水文地质条件

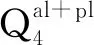
拟建场地位于汉江冲积一级阶地，地下水类型包括上层滞水和承压水两种类型，两者之间由黏性土层阻隔，无水力联系。

(1) 上层滞水：赋存于第①层杂填土层中，主要接受大气降水、地表水和周边居民生活用水的渗透补给，水量随季节变化较大，无统一的自由水面，水量与周边排泄条件关系密切。勘察期间测得上层滞水的水位在地面下1.80～3.50 m之间，相当于标高为17.89～20.18 m。

(2) 承压水：主要赋存于下部第⑤层粉砂夹粉土、粉质黏土以及第⑥层粉砂和第⑦层细砂混卵砾石层中，与长江的联系密切，主要为长江水补给，其水位随长江水位涨落而升降。测得承压水水位为地面以下8 m处，相当于黄海高程13 m。

为了满足基坑开挖要求，需将承压水水位降至5.5 m以下，即基坑内要求承压水水位降深为7.5 m。该工程基坑降水主要为承压水，故后续数值模拟中将不考虑上层滞水的影响。综合考虑本场地水文地质和周边环境条件，水文地质参数建议为：承压含水层渗透系数K取14.0 m/d，基坑降水影响半径R取260 m。

3.3 基坑涌水量数值模拟计算

3.3.1 数值模型构建

本文利用有限差分数值软件MODFLOW，针对汉口客运中心基坑进行建模，通过设置不同悬挂式止水帷幕工况，对不同止水帷幕工况下基坑涌水量进行数值模拟计算，以验证本文理论公式(10)计算结果的精确度。

对汉口客运中心基坑进行概化，将其概化为260 m×130 m的矩形基坑，建模区域为1 000 m×900 m，地面标高为21 m，基岩底面标高为-31 m，建立的汉口客运中心基坑数值模型三维图，见图5。将该基坑地层条件概化为4层：杂填土层(①)、黏土层(②～④)、砂层(⑤～⑦)和基岩(⑧)，对应理论计算模型中的承压含水层和上、下隔水层。该基坑内均布设置有18口降水井，井深为40 m，滤管位置在地面以下20～39 m。上层滞水水位标高为19 m，承压水水位标高为13 m，止水帷幕落深为30 m，止水帷幕厚度为0.8 m。

3.3.2 现场抽水试验与模型验证

结合现场单井抽水试验数据对建立的基坑数值模型进行验证，抽水井为12号降水井，观测井有两口，分别为止水帷幕内41号观测井、止水帷幕外13号观测井，距抽水井的距离分别为21.3 m、22.7 m。该基坑抽水井和观测井的平面位置，见图6。

图6 汉口客运中心基坑抽水井和观测井平面位置图

根据现场实测数据，12号抽水井的泵量为360 m3/d，在模型中设置相同值并进行抽水，同步观测41号、13号井中的水位降深，绘制其水位降深实测曲线，并将降深实测曲线与数值模拟曲线进行了对比，见图7。

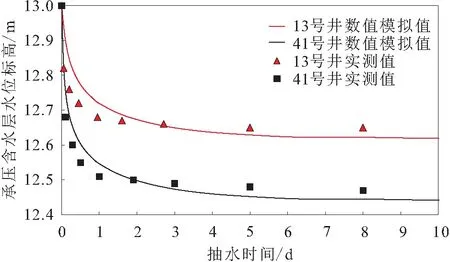
图7 汉口客运中心基坑承压含水层水位降深实测曲线与数值模拟曲线的对比

由图7可见：基坑承压含水层水位降深实测曲线在前期下降的速率稍大于数值模拟曲线，但两者最大水位降深基本一致，基坑内41号井实测和数值模拟最大水位降深都接近0.48 m，基坑外13号井实测和数值模拟最大水位降深都接近0.37 m。

上述结果表明，本文建立的数值模型能反映出该承压含水层、悬挂式止水帷幕基坑的地下水渗流情况。

3.3.3 数值模拟结果与理论公式计算结果的对比

数值模型计算参数与理论公式计算参数的赋值相同，其中承压含水层的渗透系数K取14.0 m/d，只改变止水帷幕落深和基坑开挖深度来研究基坑涌水量Q的变化，数值模型计算工况见表3。其中，基坑开挖深度的改变通过改变抽水井的泵量来实现，不同的基坑开挖深度对应不同的场区内水位降深，在基坑内均布有18口抽水井，泵量从500 m3/d、600 m3/d到700 m3/d依次改变以达到不同基坑开挖深度所需的水位降深；同时，改变止水帷幕深度，观察基坑开挖深度和帷幕深度对基坑涌水量的影响。汉口客运中心基坑涌水量数值模拟结果与理论公式计算结果的对比，见图8。

表3 基坑数值模型计算工况

图8 汉口客运中心基坑涌水量数值模拟结果与理论公式计算结果的对比

由图8可见，该基坑涌水量的数值模拟结果与理论公式计算结果之间的相对误差仅为9%左右，且变化趋势基本一致，表明本文提出的承压含水层、考虑悬挂式帷幕影响下的基坑涌水量理论计算公式是合理且可用的，对于基坑工程实际具有参考意义。但其数值模拟结果稍大于理论计算结果，这与第2节的验证结果一致，这是因为理论公式计算模型更加理想化，即将上、下隔水层和止水帷幕均假设为绝对不透水，且止水帷幕附近的地下水渗流路径均为沿着止水帷幕边缘，故基坑涌水量理论公式的计算结果小于数值模拟结果。

3.4 基坑涌水量理论计算公式参数的影响分析

以汉口客运中心基坑为基础，对基坑涌水量理论计算公式(10)中参数对基坑涌水量和基坑外水位降深的影响进行了分析，其中K=14.0 m/d，D=0.8 m，M=26 m，Mr=17 m，R=260 m，r0=103.7 m，s0=7.5 m。基坑面积、止水帷幕深度和基坑设计水位降深对基坑涌水量和基坑外水位降深的影响曲线，见图9至图11。

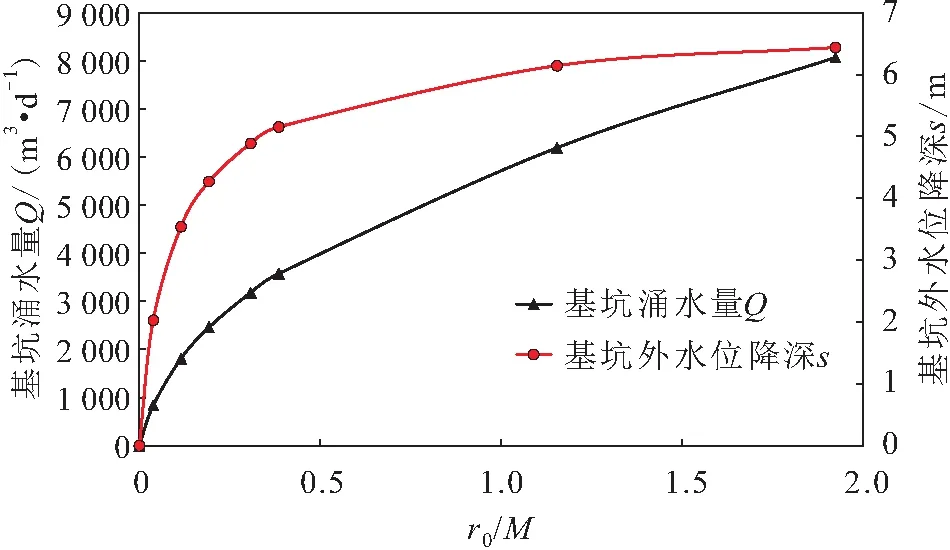
图9 基坑面积对基坑涌水量和基坑外水位降深的影响曲线

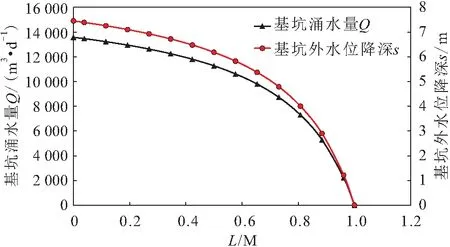
图10 止水帷幕深度对基坑涌水量和基坑外水位降深的影响曲线

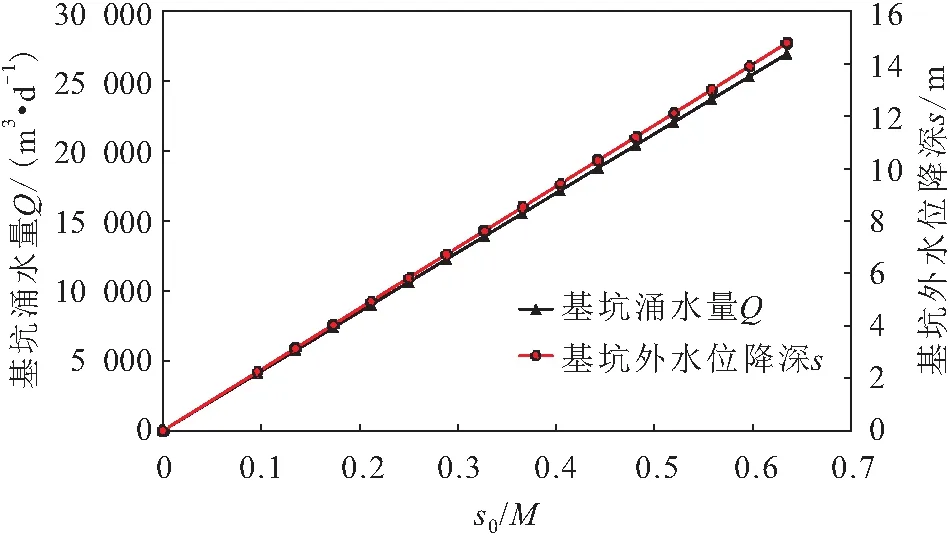
图11 基坑设计水位降深对基坑涌水量和基坑外水位降深的影响曲线

由图9可知：当r0/M≤0.4时，基坑面积对基坑外水位降深s的影响较大，随着基坑面积的增大，基坑外水位降深s的增速逐渐减缓；当r0/M≤0.4时，基坑涌水量Q随基坑面积的增大而增大，且在r0/M>0.4后，基坑涌水量的增速逐渐趋于稳定。需要指出的是，本文建立的基坑涌水量理论计算公式将不同形状的基坑按面积等效为圆形基坑，并未考虑基坑平面形状的影响。

由图10可知：当L/M<0.6时，止水帷幕深度的增加对基坑涌水量Q的影响较小，当L/M≥0.6时，止水帷幕深度的增加对基坑涌水量的减小效果显著；基坑外水位降深s的变化规律与基坑涌水量Q的变化规律相似；当L/M=1即止水帷幕落底时，基坑涌水量Q=0，该结果与理论公式(10)的计算模型相符，即不考虑止水帷幕渗漏和基岩裂隙水的存在，此时基坑内不存在补给项。

由图11可知，基坑涌水量Q和基坑外水位降深与基坑设计水位降深s0呈线性正相关关系。

综合以上计算结果，表明理论公式(10)满足基坑涌水量与止水帷幕深度呈反比、与基坑面积和基坑设计水位降深呈正比的客观规律。相比于JGJ 120—2012中的基坑涌水量计算公式，本文建立的理论公式(10)反映出了止水帷幕的有利作用，可为不同承压含水层条件下基坑工程提出止水帷幕插入深度的经验有效值，也可为现场基坑降水井的布置数量和方式优化提供依据。

4 结 论

本文基于Dupuit稳定承压井流理论，考虑了悬挂式止水帷幕对地下水水力梯度和渗流断面的影响，对承压含水层、悬挂式止水帷幕条件下基坑涌水量的计算公式进行了理论推导，并通过基坑工程案例基坑涌水量实测结果和数值模拟结果与理论公式计算结果的对比，验证了该理论公式的准确性，并得到以下结论：

(1) 根据渗流理论分析，悬挂式止水帷幕影响基坑涌水量的关键在于其对地下水水力梯度和渗流断面的影响。越靠近止水帷幕处地下水水力梯度越小，且止水帷幕插入承压含水层一定厚度后会减小渗流断面的影响，两种因素都会造成基坑涌水量的减小。

(2) 基于悬挂式止水帷幕基坑地下水渗流特点，在大井法基础上对《建筑基坑支护技术规程》(JGJ 120—2012)中基坑涌水量计算公式进行了修正，得出承压含水层、考虑止水帷幕条件下基坑涌水量的理论计算公式，其符合地下水动力学及渗流原理，具有一定的理论科学性。通过相关基坑工程案例基坑涌水量实测结果和数值模拟结果与理论公式计算结果的对比，证明该理论公式在实际基坑工程应用中具有较高的准确度和可行性，可为实际基坑工程中存在止水帷幕条件下基坑涌水量的计算提供参考，方便现场降水井的施工优化，具有较强的实用性。

(3) 通过对基坑涌水量理论计算公式中参数对基坑涌水量的影响进行分析发现，当r0/M≤0.4时，基坑面积对基坑外水位降深s的影响较大；当L/M≥0.6时，止水帷幕深度的增加对基坑涌水量的减小效果显著。相比于JGJ 120—2012中基坑涌水量计算公式，本文建立的基坑涌水量理论计算公式反映出止水帷幕的有利作用，可为不同承压含水层条件下的基坑工程提出止水帷幕插入深度的经验有效值，也可为现场基坑降水井的布置数量和方式优化提供依据。

值得注意的是，实际基坑工程中绕流区地下水水力梯度的变化应该是非线性的，但本文的理论计算公式对其做了线性均值处理，使得理论公式的计算结果与实测值相比偏小；此外，理论计算公式将不同形状的基坑按面积等效为圆形基坑，并未考虑基坑平面形状的影响，这将有待进一步的研究。