基于模糊贝叶斯网络的化工园区火灾爆炸事故情景推演
宋英华,刘子奇,刘 丹*,方丹辉
(1.武汉理工大学中国应急管理研究中心,湖北 武汉 430070;2.武汉理工大学安全科学与应急管理学院,湖北 武汉 430070)
我国是世界上第一化工大国,危险化学品生产经营单位达21万家,涉及2 800多个种类,在国民经济和社会发展中具有重要地位。化工产业迅速发展的同时,仍存在安全管理体系不完善、重效益轻安全、重大安全风险隐患集中、园区规划建设不规范等问题,导致重特大事故时有发生,如“8·12”天津滨海新区爆炸事故、江苏响水“3·21”特别重大爆炸事故。2021年2月,中共中央办公厅国务院办公厅印发了《关于全面加强危险化学品安全生产工作的意见》,并指出“要全面加强危险化学品安全生产工作,有力防范化解系统性安全风险,坚决遏制重特大事故发生”。据统计,在各类化工安全事故中,火灾爆炸事故占比超过70%,具有普遍、多发、严重的特点。因此,分析化工园区火灾爆炸事故的风险因素及其相互作用关系,梳理事故发展脉络,研究事故演化机理,防范事故风险,提升应急管理水平,成为重中之重。
上述研究大多是从化工园区火灾爆炸事故致因的风险因素出发,主要考虑事故情景演化的不确定性,较少考虑风险因素的耦合性和模糊性以及化工园区应急能力对事故发展的影响,未对整体事故进行切片,对切片而成的各情景知识元进行模糊处理。鉴于此,本文综合考虑实际化工园区火灾爆炸事故发展具有模糊性、不确定性、信息不完全等特点,并考虑化工园区的应急能力,基于“情景-应对”的研究视角,分析了化工园区火灾爆炸事故情景产生及转化的要素耦合,采用模糊贝叶斯网络模型对事故进行了情景推演。
1 化工园区火灾爆炸事故情景表示
1.1 化工园区火灾爆炸事故情景演化分析
了解化工园区火灾爆炸事故的演化过程与规律是建立事故推演模型的基础和前提,危险因素是事故演化的驱动力,危险因素产生并不一定引发事故,但随着危险要素的增加和交织以及与应急措施的耦合将导致情景转化。通过搜集整理我国典型化工园区火灾爆炸事故案例,归纳总结了其关键情景演化发展的规律,见表1。
由表1可知,我国发生的几起化工园区火灾爆炸事故的主要成因类型为操作失误、设备本质安全化不高、违规违章、泄漏。事故往往由多要素耦合引起,且引起事故发生的直接原因往往都与人的行为有关,因此人的行为是化工园区火灾爆炸事故分析的关键因素。其次,一旦发生火灾爆炸事故,发展速度极快,会对周边环境造成影响,从而引发次生灾害。初始情景发生后决策者会制定应急措施以控制事故继续恶化,后续情景是以初始情景为起点,通过各组成要素输入到下一情景,不断向前演化。事故情景推演存在两种不同的路径,一种是向期望方向发展,事故快速平息,达到损失最小;另一种是事故不断恶化,造成重大人员伤亡和财产损失。
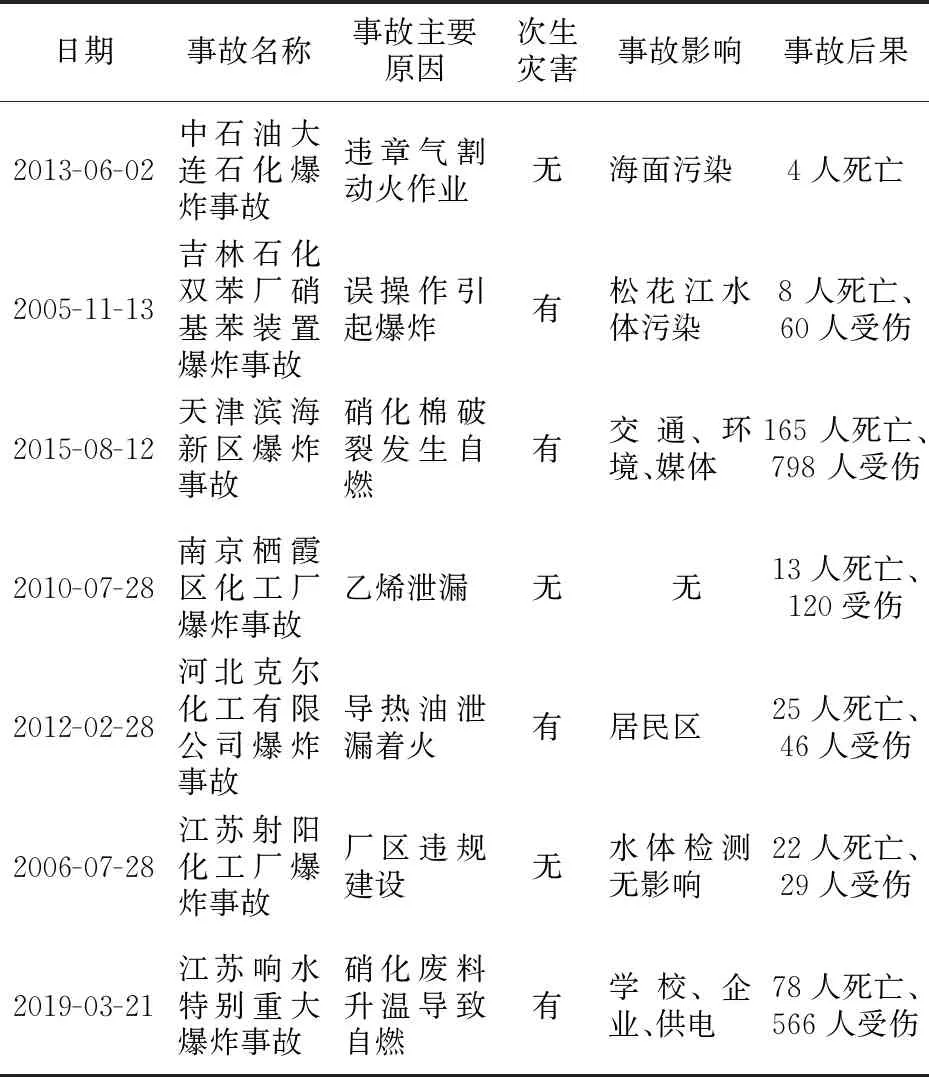
表1 我国化工园区火灾爆炸事故典型案例
1.2 知识元理论与情景知识元组成要素
知识元是不可再分割的具有完备知识表达的知识单位,是显性知识的最小可控单位[12]。对事物对象集合M中的任一对象m,基于模型共性知识元描述如下:
(1)

通过上述工业园区火灾爆炸事故情景演化规律的总结,并结合公共安全体系的“三角形模型”,将化工园区火灾爆炸事故情景知识元要素分为情景状态(S)、人的行为(H)、承灾体(E)和应急管理(M)四类,见图1。

图1 化工园区火灾爆炸事故情景知识元要素组成
(1) 情景状态(S):表示突发事件从发生至结束所有关键的情景节点,关键情景的转换构成事件发展的全过程,包括发生时间、发生地点、影响后果、影响范围、持续时间等要素。
(2) 人的行为(H):是指人为动作对事故发生发展造成的直接或间接影响,包括技术失误、违规操作、组织氛围、资源管理、过程漏洞等要素。
(3) 承灾体(E):是指突发事件发生过程中受到直接或间接影响,造成危险状态产生的受灾体。在化工园区火灾爆炸事故中,承灾体一般为厂区或具体设备,包括外部规划、园区布局、工业设备等要素。
(4) 应急管理(M):是指在每个情景状态发生后,企业或相关负责人员为避免事情恶化所采取的应对措施,包括监测预警、救援措施、资源保障、应急决策等要素。
2 模糊贝叶斯网络的构建
2.1 贝叶斯网络
2.1.1 简单贝叶斯网络
贝叶斯网络是一个有向无环图,由代表变量的节点以及连接这些节点的有向边构成。节点代表随机变量,节点间的有向边代表了节点间的相互关系(由父节点指向其子节点),采用条件概率表达节点间的关系强度,没有父节点的节点采用先验概率进行信息表达。贝叶斯网络包含S1、S2、S33个节点,其中S1和S2为S3的父节点,S3为子节点;通过条件概率表示两节点间联系的强度,即P(S3|S1)和P(S3|S2)分别表示在节点S1和S2发生的条件下S3发生的条件概率,S1、S2没有父节点,其概率P(S1)、P(S2)采用先验概率表示,见图2。

图2 贝叶斯网络示意图
设父节点为x,子节点为y,依据贝叶斯网络具有条件独立性,其全概率公式可表示如下:
P(y)=P(y|x)
=P(yx1+yx2+…+yxn)
=P(yx1)+P(yx2)+…+P(yxn)
(2)
由公式(2)可知,全概率公式是根据父节点和节点间的概率关系计算得到子节点的后验概率。
贝叶斯概率公式与全概率公式相反,用于在已知事件一定发生时,推算引起事件发生的原因。贝叶斯概率公式可表示如下:
(3)
2.1.2 事故情景演化的贝叶斯网络构建
根据事故情景演化过程,构建贝叶斯网络,具体步骤如下:
(1) 确定节点。根据以往的情景知识元的组成要素,构建对应的节点类型,以“突发事件”为核心,将同一情景知识元内的要素节点归总,并确定各要素的类型和取值范围。
(2) 确定节点变量间关系。首先定位串起整个情景链的核心“突发事件”关键节点,依据时间顺序将情景节点展开,在情景演化期望发展方向向右横向铺开,非期望发展方向向下纵向铺开,将每个情景知识元内的各要素节点按规律排列,用有向线连接节点形成贝叶斯网络。
(3) 计算节点概率。节点概率可分为先验概率、后验概率和条件概率。其中,后验概率根据先验概率和条件概率求出;先验概率和条件概率通常依据专家打分得出。
2.2 模糊贝叶斯网络构建
模糊贝叶斯网络构建是以模糊集合理论为基础,结合事故情景演化的贝叶斯网络,针对信息获取不完全、节点变量概率不确定、专家打分主观性强等影响情景推演准确程度的不利因素而提出,目的是得到更加精准、可信度高的情景推演结论。在实际问题中,要素节点间的关系并非都是0和1的关系,往往存在一定的模糊性,如专家判断节点的影响程度或是重要性,往往给出如“比较高”“较低”“中等”等模糊性语言,而非具体量化的概率值。对此,引入模糊理论对专家模糊评价进行量化处理。
2.2.1 模糊数
模糊集是指用于表示界限或边界不分明的具有特定性质事物的集合,其基本思想是把经典集合中的绝对隶属关系灵活化,隶属度不再局限于取0和1,而是可以取0~1之间的任一数值,常用的是三角模糊数和梯形模糊数。对于三角模糊数A(a,b,c),隶属度函数f(x)可表示如下:
(4)
其中,λ截集为Aλ=[(b-a)λ+a,(b-c)λ+c]。
对于梯形模糊数A(a,b,c,d),隶属度函数f(x)可表示如下:
(5)
其中,λ截集为Aλ=[(b-a)λ+a,-(d-c)λ+d]。
2.2.2 模糊语言转化和专家权重
模糊语言转化需要对节点概率进行合理程度划分,节点概率的划分过少将会影响情景推演的精确程度,节点概率的划分过多又会导致专家打分和计算的成本过高。因此,本文参考文献[13]将事件发生的概率分为非常高(VH)、高(H)、偏高(FH)、中等(M)、偏低(FL)、低(L)、非常低(VL)7 个语言变量,对应的模糊数和截集,见表2。

表2 事件发生概率的模糊数和截集
综合三角模糊数和梯形模糊数,将专家判断(模糊语言)转化为模糊数,采用线性意见池的方法获得多个专家的综合评判结果为
(6)
式中:Aim表示第i个要素的第m个专家评判的模糊值;m表示专家总数。
2.2.3 模糊数求解
进一步采用Lious提出的积分值法[14],利用隶属度函数的截集进行运算,对模糊数进行解模糊,得到具体的概率值,其计算公式如下:
I=αμR(A)+(1-α)μL(A)
(7)
式中:I为模糊数的代表值;α为乐观系数,α∈[0,1],当α=0、1 时分别对应模糊化值的上、下界,当α=0.5时为模糊数A解模糊化值的代表值;μR(A)和μL(A)分别为模糊数A左、右隶属度函数的积分值,其计算公式为
(8)
(9)
其中:mλ、nλ为模糊数A截集的上、下界;λ=0,0.1,…,0.9;Δλ=0.1。
3 实例验证与分析
3.1 案例描述
本文以内蒙古东兴化工“4·24”爆炸事故为例进行实例分析。2019年4月24日2时34分,内蒙古伊东集团东兴化工有限责任公司氯乙烯气柜气体泄漏扩散至电石冷却车间,遇火源发生燃爆,造成4人死亡、3人重伤、33人轻伤,直接经济损失达4 154万元。根据内蒙古自治区应急管理厅公布的事故调查报告,事发当日正值大风天气,又因地形因素的影响产生安全隐患,从交接班至爆炸发生共经历了2小时35分。通过梳理该事故发生过程中的重要情景,查找工作人员的应对措施,并按时间顺序排列,得到事故发生过程图,见图3。

图3 内蒙古东兴化工“4·24”爆炸事故发生过程图
3.2 事故情景表示与贝叶斯网络构建
依据图3的事故发生过程,得到12个情景节点(S1~S12),见表3,其中4个关键情景节点(S1、S3、S6、S9),构建的该事故贝叶斯网络情景推演图,见图4。

表3 情景知识元

图4 内蒙古东兴化工“4·24”爆炸事故贝叶斯网络情景推演图
3.3 模糊贝叶斯网络分析
3.3.1 专家语言的模糊化处理
依据5位相关领域专家对节点发生的可能性,使用非常高(VH)、高(H)、偏高(FH)、中等(M)、偏低(FL)、低(L)、非常低(VL)7个语义值进行的模糊评判,以节点S1为所在的情景知识元为例,5位专家分别给出E1高、非常高、非常高、偏高、非常高5个模糊概率语言描述,利用表2中对应的关系将模糊数转化为截集形式,并依照公式(6)进行线性处理,得到该节点综合模糊数的截集形式如下:
3.3.2 模糊数的求解
收集和计算出专家对每一个初始节点给出的综合模糊值,并根据综合模糊值进行解模糊,得到每个节点的精确概率值。以E1节点综合模糊值为例进行计算,有:
I=αμR(A)+(1-α)μL(A)=0.5×(-0.01+0.94)+0.5×(0.05+0.72)=0.85
得到P(E1=T)=0.85,P(E1=F)=0.15。同理,可计算得出其他各节点变量的先验概率,部分计算结果见表4。

表4 节点变量的条件概率
3.3.3 贝叶斯网络概率推理
采用Netica软件进行贝叶斯网络建模,将计算得到的数据输入到各状态节点中,见图5。

图5 贝叶斯网络情景节点概率
由图5可以看出:
(1) 关键情景状态节点(S1、S3、S6、S9)中,除初始情景状态外,发生概率最大的情景状态为爆炸(S9),其次分别是氯乙烯气柜卡顿泄漏(S3)和氯乙烯气体大量泄漏扩散(S6)。大风天气(S1)是本次事故情景的初始情景状态,承灾体在一开始给予事故一个非常高的发生概率,该问题的产生说明企业在厂区的建设方面未考虑到大风天气及其影响,因此需要抓紧补足这方面的不足,现有的应急措施应从人的行为和应急管理两方面入手。节点中发生次生灾害(S11)概率最低为44.3%,由于救援及时并且转移了危险品,因此次生灾害发生概率较低,并且事故消亡类的情景状态中,S10作为发生次生灾害前的节点,既反映了事故发展的实际情况也恰好说明事故从该节点消亡的可能性是最大的。因此,计算结果与事故实际发展相符,说明该模型具有有效性。
(2) 情景事件中氯乙烯气体大量泄漏扩散(S6)的发生概率相对较低,并且该环节承灾环境方面对事故发展起利好作用,说明目前在氯乙烯气柜卡顿泄漏后采取的应对措施相对于其他节点最能有效避免事故恶化,也说明该环节现有的应急预案和应急措施相对最为有效。
(3) 关键情景状态节点中爆炸(S9)的发生概率最高,说明在氯乙烯气体大量泄漏扩散(S6)发生之后,事故发展速度较快,现有的应急管理方法和外部环境不足以化解已有的危险,所以事故大概率会发生。因此,加强设备的检修,加装报警设备和对氯乙烯气体泄漏进行定期检测是避免事故发生的有效措施。
4 结 论
(1) 为量化分析化工园区内火灾爆炸事故的风险因素,从“情景-应对”研究视角出发,利用情景知识元,通过“情景状态、人的行为、承灾体、应急管理”四类知识元要素表达情景,不仅能定量化分析事故发生的原因,还能推演事故进行风险评估与预测。
(2) 基于模糊贝叶斯网络进行事故情景推演,将不确定性模糊信息进行定量化的描述,在很大程度上克服了专家打分的主观性和要素数据不完全的问题,并利用三角模糊数和梯形模糊数结合的隶属度函数将事故发生概率分级细化,提高事故情景推演的精确程度。
(3) 基于模糊贝叶斯网络的情景推演方法可以准确地描述事故的发展过程,实现对案例正向推理预测事故走向和逆向推理判断薄弱环节的目的,可为防范事故风险、完善应急预案、辅助应急决策提供技术支撑。

