程序设计中两个典型问题的关联与启示

摘要：各种高级语言程序设计类教程通常都会涉及两类问题的编程——棋盘麦粒计数问题和汉诺塔金片移动问题，但并没有发现、更没有证明两者之间的关联性，也没有深入到启示层面。在文章中不仅给出了答案，而且还具体到课程教学中如何设置提问、如何引导学生思考，达到思维训练和创新能力培养的目的。由此可见对编程类人才培养有参考价值。

关键词：程序设计;教学;思维;认知;大数据

中图分类号：TP311      文献标识码：A

文章编号：1009-3044（2022）10-0104-03

1 引言

当今的世界是处于大数据和人工智能的时代，迫切需要掌握算法及编程的技术类人才，高等学校如何面向市场需求、向社会输送合格学生是一个重要的研究课题。目前这方面的研究文章很多，但大多数局限于抽象的讨论，具体应用于课堂的价值不大。作为直面学生的一线老师，更需要落到实处的解决方案，此文从两个典型问题出发，较深入细致地探究课堂教学及人才培养，希望能达到“抛砖引玉”的效果。

2 典型问题之一——棋盘麦粒的计数

有一个古老的印度传说：舍罕王要奖赏宰相达依尔——国际象棋的发明人。国王询问他想要什么样的奖赏？他回答说：“陛下在这张棋盘的小格子放一些麦子，第1格放1粒麦子，第2格放2粒，第3格放4粒，总之，后面格子里麦粒数量总是前面格子里的2倍。这样摆满了64个格子的棋盘上所有的麦粒，就是您对仆人的奖赏！”

国王感到这要求实在太简单了，马上令人扛来麦子，但很快就不够用了。于是人们将一袋袋麦子搬来计数时，大家才发现：就算将整个印度的麦粒都取来，也达不到宰相的要求。

宰相到底要多少麦粒？若体积 1 立方米的麦粒大约有 [1.42×108]颗，问宰相要求的麦子为多少立方米[1]？

依据题意，编写C语言程序（qpmn1.c）如下：

#include "stdio.h"

#include <stdlib.h>

int main（）

{double t;           //t表示麦粒体积

double s = 0;       //s表示麦粒总数

double n = 1;       //n表示小格子麦粒颗数

int j;

for（j=1; j<=64; j++）

{s=s+n;        //各格子麦粒累加

n=n*2;        //小格子麦粒数

}t=s/（1.42*100000000）;

printf（"s=%.lf颗麦粒＼n"，s）;   //麦粒的颗数

printf（"t=%.lf立方米麦粒＼n"，t）;   //麦粒的体积

system（"pause"）;

return 0;

}

运行得到：s=18446744073709552000颗麦粒，t=129906648406立方米麦粒。这是两个非常庞大的数量，按当时的生产力估算：用两千年的时间，全世界也难以生产出宰相要的这么多麦子[1]。

注意到这个问题本质是要计算[20+21+22+23+...+262+263]的值，由等比数列的前n项和公式得：[20+21+22+23+...+262+263=264-1]，下面编程计算[264-1]的值（由新算法产生新程序） ，得到简化的C程序代码（qpmn2.c）如下[2]：

#include "stdio.h"

#include <math.h>

int main（）

{int x = 2，y，i;

double result;

printf（"input y："）;

scanf（"%d"，&y）;

for（i=1;i<=y;i++）

{result = pow（x， i）;

result=result-1;

printf（"%.lf  "，result）;

if（i%4==0） printf（"＼n"）;

}getch（）;

return 0;

}

程序運行结果如下：

运行结果的64个数据是[21-1]，[22-1]，[23-1]，...[263-1]，[264-1]的计算结果。之所以这样编程是为了进行数据比对，看到数据的变化过程，[2i-1（i=1，2...64）]表示的是前面i个棋盘格子的麦粒总数。在C语言的教学过程中，要引导学生发现问题和解决问题，培养学生的独立思考能力和创新能力。在此提问：运行结果有错误吗？如果有错，错在什么地方呢？64个数据[2i-1（i=1，2...64）]应该都是奇数，但最后的11个数据却是偶数，所以一定是错的。在程序中用result存储运算结果，定义为双精度实型（double result;） ，而double型数据只能保证15位有效数字，千万不要认为电脑输出的数字都是绝对精确有效的。若修改为无符号双长整型（unsigned long long result;） 程序代码（qpmn3.c）如下[2]：

#include "stdio.h"

#include <math.h>

int main（）

{int x = 2，y，i;

unsigned long long result;

printf（"input y："）;

scanf（"%d"，&y）;

for（i=1;i<=y;i++）

{result = pow（x， i）;

result=result-1;

printf（"%lld  "，result）;

if（i%4==0） printf（"＼n"）;

}

getch（）;

return 0;

}

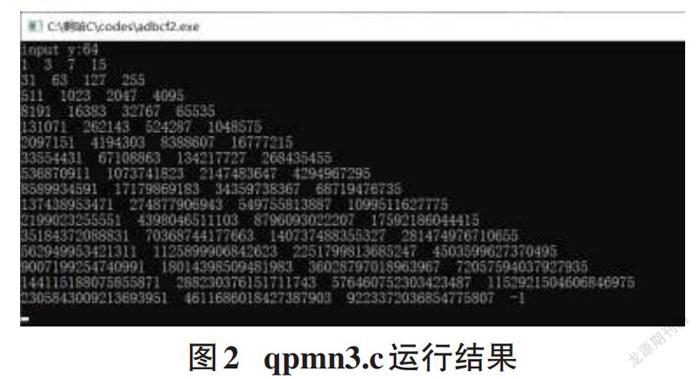
运行结果如下：

注意到最后的11个数据有10个已修改正确，但最后1个发生了数据溢出错误[3]。

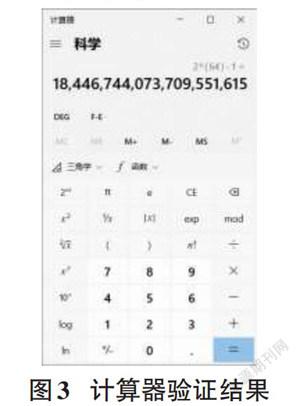
验证一下：用Windows自带计算器选科学型可得[264-1=]18446744073709551615，而程序运行结果是18446744073709552000，两者有误差。

为什么用C语言计算庞大的数会产生错误？这个问题作为作业留给学生思考。

梳理一下思路：这个问题的计算或编程都是比较简单的，国王贸然答应宰相，是对数量缺少正确的认知，是对按几何增长的数量估算不足。常言道“不算不知道，一算吓一跳”，宰相戏弄了国王，国王有惩罚的手段吗？C语言课程教学中作为作业让学生思考，可在一个星期之后给出答案……答案是：国王要惩罚宰相必须抓住问题的关键点——麦粒数量庞大。

让宰相亲自到粮仓去数麦粒，假定1秒钟能数2粒麦子，每天数12小时，需要10年才能数出20立方米。要数完那么多麦粒将需要2900亿年……宰相能活多少年？再有每天数麦子的活法谁能承受？如此数下去人会疯掉……这类作业可拓展思维、启迪智慧[4]。

3 典型问题之二——汉诺塔金片的移动

汉诺塔问题——印度另一个古老的传说，大梵天开天辟地时做了3根宝石针，其中一根针上穿好了64片金片，金片大小不等，从下到上按由大到小的顺序。大梵天下指令让婆罗门按照以下法则移动金片：一次只能移走一片，无论在哪根针上，小片要在大片的上方。3根宝石针分别用A、B、C做标记，初始状态是A针上有64片金片，目标是将A针上的金片借助于B针全部移到C针上，请找出移动金片的步骤。

用C语言编程时要用到函数的递归调用，几乎所有的C语言教程都要写入这个典型实例，给出相关的程序代码，运行得到金片的移动步骤。下面的程序代码（hanoi_tower1.c） 有新颖的地方，对传统程序做出了改进，增加了标识和统计移动步骤的功能[5]。

#include <stdio.h>

int js=1;

int main（）

{void hn（int n，char z1，char z2，char z3）;

int m;

printf（"Please input the num of gold diskes："）;

scanf（"%d"，&m）;

printf（"The moving-step  %d gold diskes：＼n"，m）;

hn（m，'A'，'B'，'C'）;

getch（）;

return 0;

}

void hn（int n，char z1，char z2，char z3）

{void mv（char x，char y）;

if（n==1）

mv（z1，z3）;

else

{hn（n-1，z1，z3，z2）;

mv（z1，z3）;

hn（n-1，z2，z1，z3）;

}}

void mv（char x，char y）

{ printf（"%d："，js）;

printf（"%c-->%c＼n"，x，y）;

if（js % 10==0） getchar（）;

js++;

}

程序運行时5片金片的移动步骤如下：

Please input the num of gold diskes：5

The moving-step  5 gold diskes：

1：A-->C  2：A-->B  3：C-->B  4：A-->C  5：B-->A  6：B-->C  7：A-->C

8：A-->B  9：C-->B  10：C-->A  11：B-->A  12：C-->B  13：A-->C  14：A-->B

15：C-->B  16：A-->C  17：B-->A  18：B-->C  19：A-->C  20：B-->A  21：C-->B

22：C-->A  23：B-->A  24：B-->C  25：A-->C  26：A-->B  27：C-->B  28：A-->C

29：B-->A  30：B-->C  31：A-->C  （程序实际运行得到31行，太占篇幅，这里做了合并）

注意：5片金片的移动步骤前7次恰好就是3片金片的全部移动步骤，这不是偶然的而是必然的。也就是说n片金片的全部移动步骤是n+2片金片最前面的部分移动步骤（“隔代遗传”） ，为什么有这样的结论？在这里要设置课堂互动，让同学们思考后回答[6]。

若程序中删去if （js % 10==0） getchar（）;这一行，运行时若输入35到64之间的较大自然数时，屏幕不断向上翻滚显示移动步骤，一直停不下来，这是为什么呢？仔细思考一下，莫非是电脑已得到结果，但显示器的显示速度跟不上？64片金片至少需要移动多少次才能实现目标呢？这个经典问题的答案是至少需要移动18446744073709551615次。假如金片移动1次需要1秒，则共需18446744073709551615秒时间。平年有365天是31536000 秒，闰年有366天等于31622400秒，每年平均下来是31556952秒，计算结果是移完这些金片需要5845.54亿年以上（18446744073709551615秒） ，然而地球至今存在不超过45亿年，太阳系预期寿命科学家们预测也不过数百亿年。如若超过5845.54亿年，太阳系、银河系、地球上的生物、庙宇、梵塔等，都早已灰飞烟灭。

为了验证前面的解决方案是不是因为显示器的显示速度跟不上，修改程序不显示金片的移动步骤、只统计移动次数的功能（hanoi_tower2.c）  [6]。

#include <stdio.h>

double js;

int main（）

{void hn（int n，char z1，char z2，char z3）;

const t=32;

int m;

for（m=1;m<=t;m++）

{js=0;

hn（m，'A'，'B'，'C'）;

printf（"%.lf  "，js）;

if（m%4==0） printf（"＼n"）;

}getch（）;

return 0;

}void hn（int n，char z1，char z2，char z3）

{void mv（char x，char y）;

if（n==1）

mv（z1，z3）;

else

{hn（n-1，z1，z3，z2）;

mv（z1，z3）;

hn（n-1，z2，z1，z3）;

}}

void mv（char x，char y）

{js=js+1;  //printf（"%c-->%c＼n"，x，y）;

}

程序運行结果如下：

1  3  7  15

31  63  127  255

511  1023  2047  4095

8191  16383  32767  65535

131071  262143  524287  1048575

2097151  4194303  8388607  16777215

33554431  67108863  134217727  268435455

536870911  1073741823  2147483647  4294967295

若将程序中语句const t=32;改成const t=64;运行时结果将一直出不来（递归需要时间） ，这表明电脑是边计算边输出，而不是电脑已得到结果、只是显示器的显示速度跟不上。千万不要小瞧这个结论，90%以上的计算机教师教了一辈子程序设计，仍然错误认为电脑已有答案，只是需要排队显示，数据量太大，显示需要时间等候。

4 两个典型问题的关联与启示

由前面的分析讨论可知：棋盘麦粒计数问题中，前面i个棋盘格子的麦粒总数为[2i-1（i=1，2...64）]。而汉诺塔金片的移动问题，从程序运行结果上看，i片金片至少需要移动的次数居然也是[2i-1（i=1，2...64）]，多么神奇的巧合？不是巧合是规律，下面用数学归纳法证明：

当i=1时，移动1次，[20=21-1]

当i=2时，移动3次，[20+21=22-1]

当i=3时，移动7次，[20+21+22=23-1]

假设当i=k时，移动[20+21+...+2k-1=2k-1]次，那么当i=k+1，即A针上有k+1个盘子时，操作步骤如下：

将A针上面k个盘子借助C针移动到B针上，移动次数为[2k-1]次，之后将A针上最大盘子直接移动到C针上，移动次数为1次，最后将B针上面k个盘子借助A针移动到C针上，移动次数为[2k-1]次，总共移动次数为：

[（2k-1）+1+（2k-1）=2*2k-1=2k+1-1]

结论得证[7]。

启示1：“趋乐避苦”是人性，决定了人类对数量的认知往往容易犯错误。比如初次涉及棋盘麦粒计数问题的人，不会去计算宰相要求奖励的麦粒数量到底是多少（仅凭感觉认为并不多） ？全世界的小麦产量是多少？仔细计算才发现是非常庞大的数量。正确的选择基于正确的认知——对客观世界的正确认知、对人类社会的正确认知、对自身的正确认知。“认识你自己”点燃了古希腊文明火花，“知人者智，知己者明”凝聚了中国古老的智慧。与世界这个无穷大量（[β→∞]） 相比，个人就是一个无穷小量（[α→0]） 。

启示2：“知易行难”的新解释：无论是棋盘麦粒计数问题或是汉诺塔金片移动问题，计算出总量都不难，困难的是具体的“数麦粒”和具体的“移动金片”，因为具体步骤非常庞大。推广到个人对数量的认知，大家都知道世界有75亿人，中国14亿人，但对这总量的感性认识并不够，让个人痛苦地去数一数才会有体会。很多位高權重的人、很多富有的商人容易膨胀，他们对75亿分之一、14亿分之一有多小缺少正确的认知。从这个角度看，自大的人是多么的愚蠢。“强极则辱、情深不寿、慧极必伤”是古训，“谦谦君子、温润如玉”是处世之道。

启示3：过分强调过程考核的教学评估是有很大弊端的，因为这样会把教师变成“数麦粒”的人、变成“移动金片”的人。有些学校机械地、僵化地理解评估指标体系，实则偏离了顶层设计的宗旨。试想这样为完成繁杂指标体系、收集庞大支撑材料“挥汗如雨”的教师会有多少独立思考？又怎么能培养出有创新思维的学生？

5 结束语

课程思政是各门课程课堂教学中非常重要的组成部分，正确的“三观”培养、正确的认知引导是高校人才培养的基石。这两个典型的编程案例告诉我们：“千里之行，始于足下”“不忘初心，方得始终”。在“百年未有之大变局”的时代，青年学生必须努力前行，为中华民族实现伟大复兴贡献自己的一份力量！

参考文献：

[1] 谭浩强.C程序设计[M].5版.北京：清华大学出版社，2017.

[2] 梅创社，李培金.C语言程序设计[M].北京：北京理工大学出版社，2010.

[3] 焦华.基础编程的思考方法[J].软件，2018，39（3）：57-62.

[4] 台海江，许鑫，郑光.《C语言程序设计》课程教学改革探讨[J].现代计算机（专业版），2018（33）：74-77.

[5] 焦华.C编程教学导入线索分析[J].电脑知识与技术，2017，13（12）：126-129，156.

[6] 焦华.C/C++编程中典型案例分析与思路拓展[J].电脑与信息技术，2017，25（3）：36-39，56.

[7] 安光勇.以数学算法为基础的C程序编程技巧[J].电子测试，2017（7）：76-77.

【通联编辑：谢媛媛】

收稿日期：2022-01-25

作者简介：焦华（1964—） ，男（苗族） ，贵州贵阳人，副教授，硕士，研究方向为算法与程序。