成都气溶胶散射吸湿增长因子多变量影响分析

佟景哲，倪长健①，杜云松，陈云强，张城语 (1.成都信息工程大学大气科学学院，四川 成都 610225；2.高原大气与环境四川省重点实验室，四川 成都 610225；.四川省生态环境监测总站，四川 成都 610091；.四川省气象服务中心，四川 成都 610072)

大气气溶胶是由大气介质和混合于其中的固体或液体颗粒物组成的体系[1]，由于气溶胶中的硫酸盐、硝酸盐、铵盐和海盐等无机成分及部分有机物粒子具有吸湿性，在不同水汽条件下，其粒径、质量、密度和折射指数等微物理参数会发生变化，致使气溶胶粒子群宏观上的物理、化学和光学性质不断改变[2]。气溶胶散射吸湿增长因子为相同波长条件下“湿”状态气溶胶散射系数与“干”状态气溶胶散射系数的比值[3]。作为表征气溶胶吸湿性光学效应的重要参数，气溶胶散射吸湿增长因子不仅能反映大气能见度的变化，也是用来评估气溶胶直接辐射强迫不确定性的重要因子[4-5]。

气溶胶散射吸湿增长因子随相对湿度的变化存在多种参数化方案。早在1969年，KASTEN[6]就提出气溶胶散射吸湿增长因子的γ-模型，它已经被广泛应用于卫星遥感、辐射传输模型和全球气候模式中的因子计算。SONG等[7]对γ-模型进行改进，构建了基于二次多项式的散射吸湿增长模型，可提升北京市气溶胶吸湿性模拟效果[8]。KOTCHENRUTHER等[9]提出双参数形式的散射吸湿增长模型，刘新罡等[10]基于该模型探讨了广州市海洋型、海洋/城市混合型和城市型气溶胶散射吸湿增长因子特点。此外，CHEN等[11]指出，幂指数形式的散射吸湿增长模型在天津市武清区等地区秋、冬季具有更好的适用性。综上分析可见，目前气溶胶散射吸湿增长因子模型均是以相对湿度为基础构建的单变量模型，不同模型拟合效果对气溶胶类型和区域变化具有较强敏感性。

黑碳气溶胶(BC)自身不具有吸湿性，由于其能吸附大量吸湿性物质(硫酸盐、硝酸盐和铵盐等)而对气溶胶吸湿性产生影响。研究[12-13]表明，黑碳老化可导致黑碳颗粒物在混合态、形貌、粒径和化学组成等方面发生显著变化，进而可能造成气溶胶吸湿光学效应发生显著改变。张城语等[14]基于相对湿度和黑碳质量浓度(ρBC)构建了成都地区气溶胶散射吸湿增长因子的双变量模型，显著提升了气溶胶散射吸湿增长因子的模拟精度。另外，刘凡等[15]发现，相对湿度增加会促进硫氧化率和氮氧化率，导致PM1质量浓度(ρPM1)/PM2.5质量浓度(ρPM2.5)和ρPM2.5/PM10质量浓度(ρPM10)随相对湿度增加而增大。结合气溶胶等效复折射率的实部与ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10的相关性分析成果[16]，气溶胶吸湿性在影响其粒径分布的同时，也会改变气溶胶等效复折射率的实部，从而诱发气溶胶散射吸湿增长因子的复杂响应。

气溶胶散射吸湿增长因子的演化是多变量综合作用的结果，具有高维、非线性和不确定性等特点。基于成都市2017年10—12月浊度计、黑碳仪和环境颗粒物监测仪逐时观测数据，以及该时段同时次大气能见度(V)、相对湿度(RH)和二氧化氮(NO2)监测资料，采用光学综合法计算气溶胶散射吸湿增长因子，利用广义可加模型(generalized additive model，GAM)分析相对湿度和不同气溶胶组分的协同作用对气溶胶散射吸湿增长因子的影响。

1 材料与方法

1.1 数据来源

数据包括成都市2017年10—12月浊度计、黑碳仪和环境颗粒物监测仪地面逐时观测资料，以及该时段同时次大气能见度，相对湿度和NO2质量浓度等环境气象监测数据。相关仪器如下：

(1)525 nm波长处“干”状态下气溶胶散射系数由浊度计(AURORA-3000型，Ecotech公司，澳大利亚)进行观测，采样频率为5 min·次-1，采用TSP切割头，检测范围为>0.25 Mm-1，每24 h进行零点检查，24 h零点漂移<±1%，每周采用R134a气体进行跨度标定，通过内部温湿度传感器来控制浊度计内部加热系统，使得仪器内部腔室中气溶胶相对湿度控制在40%以下，将其作为气溶胶的“干”状态。

(2)等效黑碳质量浓度(ρBC)数据由黑碳检测仪(AE-31型，Magee Scientific公司，美国)获取，其有7个测量通道，波长分别为370、470、520、590、660、880和950 nm，数据采集频率为5 min·次-1。黑碳仪采用TSP切割头，采样头与仪器连接处增设硅胶管以减少水分对黑碳测量值的影响。

(3)大气中PM10、PM2.5和PM1颗粒物质量浓度(ρPM10、ρPM2.5和ρPM1)数据由环境颗粒物监测仪(GRIMM-180，GRIMM公司，德国)实时测量，数据采集频率为5 min·次-1。

(4)大气能见度和相对湿度等气象要素由一体式气象站(LUFFT WS600，德国)进行监测，气态污染物NO2浓度由氮氧化物(NO-NO2-NOx)分析仪(Thermo 42i型，美国)进行监测。

观测点位于成都市环境保护科学研究院综合大楼楼顶(30°39′ N、104°02′ E)，距离地面高度21 m，四周2 km内无高大建筑物，视野开阔；观测点在成都市一环路以内，周围为集中居住区，5 km范围内无明显工业大气污染源。将上述监测数据统一处理为小时均值数据。首先，剔除出现降水、沙尘和大风现象所在日的全部数据；其次，剔除仪器烘干后相对湿度仍大于40%的异常数据，以排除水汽影响；最后，剔除超出界限值数据、连续无变化数据和缺测数据，由此获得匹配样本1 221个。

1.2 气溶胶散射吸湿增长因子的计算

大气消光系数为光线在大气中传播单位距离时的相对衰减率，当对比感阈值(ε)为0.05时，550 nm波长处环境大气消光系数〔bext(RH)，Mm-1〕与大气能见度(V，km)的关系式[17]为

(1)

对550 nm波长处大气消光系数进行分解，计算公式[18]为

bext(RH)=bsp(RH)+bap+bsg+bag。

(2)

式(2)中，bsp(RH)为550 nm波长处气溶胶散射系数，Mm-1；bap为550 nm波长处气溶胶吸收系数，Mm-1；bsg为大气散射系数，Mm-1；bag为吸收系数，Mm-1。

由于浊度计观测的是525 nm波长处“干”状态下气溶胶散射系数(bsp,525，Mm-1)，根据文献[19-20]，需对bsp,525进行修订得到550 nm波长处“干”状态下气溶胶散射系数(bsp)，订正计算公式为

(3)

式(3)中，α为成都市Angstrom波长指数，为1.36[21]。

黑碳检测仪直接观测得到未经订正的为880 nm波长处等效黑碳质量浓度(ρBC，μg·m-3)。参照BERGSTROM等[22]提出的订正公式，先利用ρBC反演得到532 nm波长处吸收系数(bap,532，Mm-1)，再由bap,532进一步订正得到550 nm波长处吸收系数(bap，Mm-1)，上述计算公式为

bap,532=8.28ρBC+2.23，

(4)

(5)

参照PENNDORF[23]的研究成果，550 nm波长处bsg取值一般为13 Mm-1。

bag一般仅考虑NO2的吸收，参照SLOANE等[24]计算方法，550 nm波长处bag计算公式为

bag=0.33ρNO2。

(6)

式(6)中，ρNO2为NO2质量浓度，10-9g·m-3。

基于式(1)～(6)的计算结果，采用光学综合法计算气溶胶散射吸湿增长因子(f)，其计算公式为

(7)

1.3 广义可加模型(GAM)的计算

GAM模型是加性模型的扩展，具有解释响应变量与影响因子之间非线性关系的能力。GAM模型基本形式[25]为

g(μ)=β+s1(X1)+s2(X2)+…+si(Xi)+ε。

(8)

式(8)中，g(μ)为连接函数；s1，s2，…，si为连接解释变量的平滑函数，主要包括样条平滑函数、局部回归平滑函数和三次样条函数等，该文采用样条平滑函数；Xi为解释变量；β为截距；ε为残差。为保证所建立GAM模型可靠性，采用R软件gam.check函数和压轴回归法(reduced major axis regression，RMA)对结果进行验证。

2 结果与讨论

2.1 气溶胶散射吸湿增长因子模型解释变量的选取

CHENG等[26]研究表明，颗粒物质量浓度之比在一定程度上可用来表征气溶胶组分结构信息。另外，基于文献[27]的研究成果可知，气溶胶散射吸湿增长因子(f)不仅与相对湿度变化密切相关，也对气溶胶结构和组分变化较为敏感，因此，将RH、ρBC、ρBC/ρPM1、ρBC/ρPM2.5、ρBC/ρPM10、ρPM1/ρPM2.5、ρPM1/ρPM10和ρPM2.5/ρPM10共8个因子作为f因子的初始解释变量。

由于选取的初始解释变量较多，各变量之间通常会存在多重共线性问题。多重共线性问题指回归模型中自变量之间存在高度相关性而造成模型估计失真或拟合过度，在进行GAM模型建模前应剔除可能存在多重共线性问题的解释变量。采用相关性分析和方差膨胀因子(VIF)相结合的方法对变量间多重共线性问题进行诊断。容差为某变量不能由方程中其他自变量解释的方差的占比，其值的倒数即为方差膨胀因子(VIF)。VIF是衡量多元线性回归模型多重共线性严重程度的一种度量，VIF值大于1。VIF值越大，多重共线性问题越严重。通常认为，当VIF>3时，存在严重的共线性问题，并将导致模型参数估计不稳定[28]。

由表1可知，ρBC/ρPM1与ρBC/ρPM2.5、ρBC/ρPM2.5与ρBC/ρPM10、ρPM1/ρPM10与ρPM2.5/ρPM10之间相关系数分别为0.821、0.715和0.783(均通过α=0.001的显著性检验)。解释变量间的相关系数较大时，解释变量间通常存在严重的共线性关系，在模型构建时通常只选取1个变量作为解释变量。由于气溶胶等效复折射率的实部与ρBC/ρPM2.5和ρPM1/ρPM2.5呈一定正相关关系，与ρPM2.5/ρPM10呈一定负相关关系[29]。因此，剔除解释变量ρBC/ρPM1、ρBC/ρPM10和ρPM1/ρPM10，保留解释变量ρBC/ρPM2.5和ρPM2.5/ρPM10，从而降低解释变量间的共线性问题。由表2可知，剔除解释变量ρBC/ρPM1、ρBC/ρPM10和ρPM1/ρPM10后，所有解释变量的VIF值均小于3，故以RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10这5个因子构建气溶胶散射吸湿增长因子的解释变量集。与文献[14]相比，该研究新增的ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10这3个解释变量集中反映了气溶胶结构变化和二次化学反应对气溶胶组分的影响，因而能更加全面地表征气溶胶散射吸湿增长因子受多变量影响的复杂性。

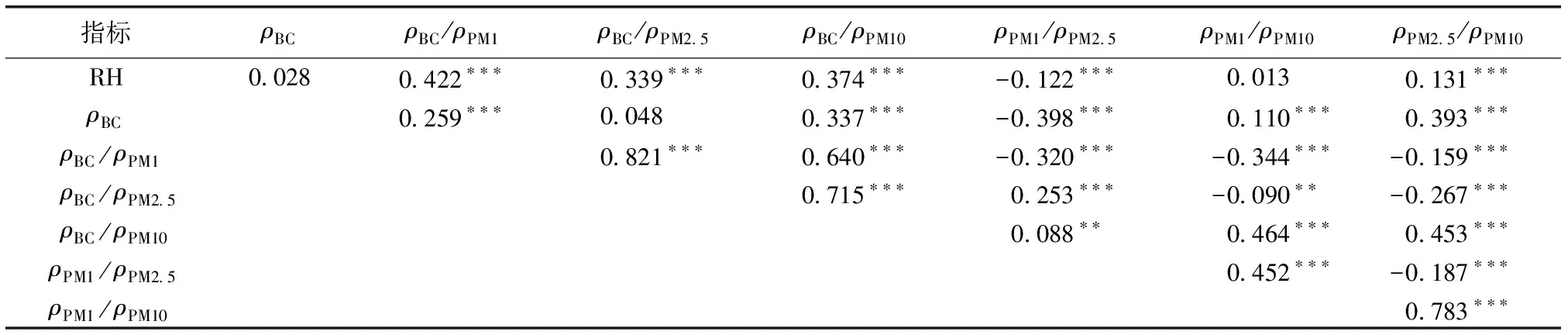
表1 解释变量的相关系数矩阵

表2 解释变量的多重共线性诊断结果

2.2 气溶胶散射吸湿增长因子单变量GAM模型分析

将气溶胶散射吸湿增长因子作为响应变量，每次在解释变量集中选取1个变量作为解释变量，利用GAM模型分析各变量对气溶胶散射吸湿增长因子的影响(表3)。表3中，变量F统计值越大，其重要程度越高；P值越小，分析结果越显著；调整后的判定系数(R2)为回归平方和与总离差平方和的比值，用于判定回归方程的拟合效果，值越大表明拟合效果越好。此外，当解释变量的自由度为1时表明解释变量与响应变量呈线性关系，自由度大于1时呈非线性关系。

由表3可知，RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10变量均对气溶胶散射吸湿增长因子存在显著影响(通过α=0.01的显著性检验)，且每个变量自由度均大于1，即气溶胶散射吸湿增长因子与解释变量集中每个变量之间均存在显著非线性关系。若响应变量与解释变量R2≥0.09，即可认为两者具有相关性[30]。由表3可知，RH和ρBC的R2分别为0.688和0.150，其值均≥0.09，表明这2个变量对气溶胶散射吸湿增长因子变化影响相对较大；ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10的R2较小，分别为0.023、0.088和0.015，表明这3个变量对气溶胶散射吸湿增长因子变化影响相对较小。ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10对气溶胶等效复折射率实部的变化具有很好的指示意义，它们反映了气溶胶组分变化同样也会导致气溶胶散射吸湿增长因子显著响应。综上可知，气溶胶散射吸湿增长因子是多变量影响下的复杂序列，具有高维、非线性和不确定性等特点。

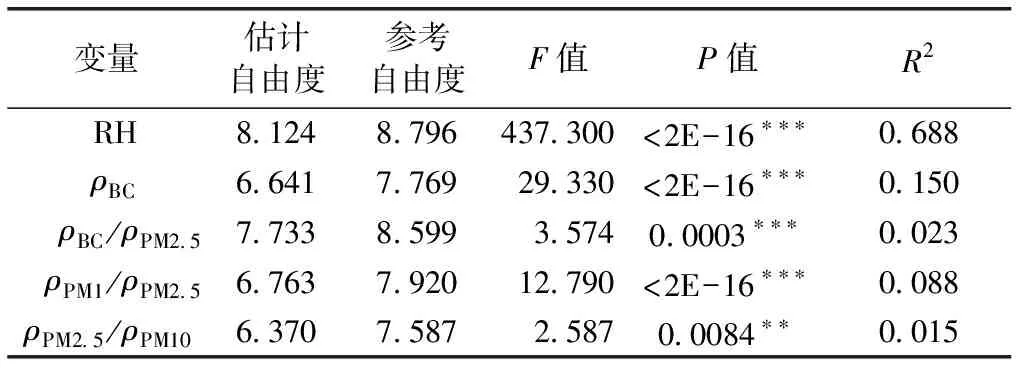
表3 气溶胶散射吸湿增长因子与单变量GAM模型的拟合结果

2.3 气溶胶散射吸湿增长因子多变量GAM模型的构建

基于解释变量集进一步构建气溶胶散射吸湿增长因子多变量影响的GAM模型，拟合结果见表4。由表4可知，RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10均通过α=0.001的显著性检验，即这5个解释变量均具有显著统计学意义；另外，结合各变量参考自由度可知，气溶胶散射吸湿增长因子与RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10均存在显著非线性关系。各解释变量F统计值结果表明，变量对气溶胶散射吸湿增长因子影响程度由高到低依次为RH>ρBC>ρPM2.5/ρPM10>ρBC/ρPM2.5>ρPM1/ρPM2.5，其相对贡献率分别为87.42%、9.66%、1.27%、1.14%和0.51%。这表明，除RH外，气溶胶组分(ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10)也是影响气溶胶散射吸湿增长因子的重要因素，其中，ρBC的影响尤为明显。气溶胶散射吸湿增长因子多变量GAM模型调整后的判定系数为0.787，模型拟合效果良好。

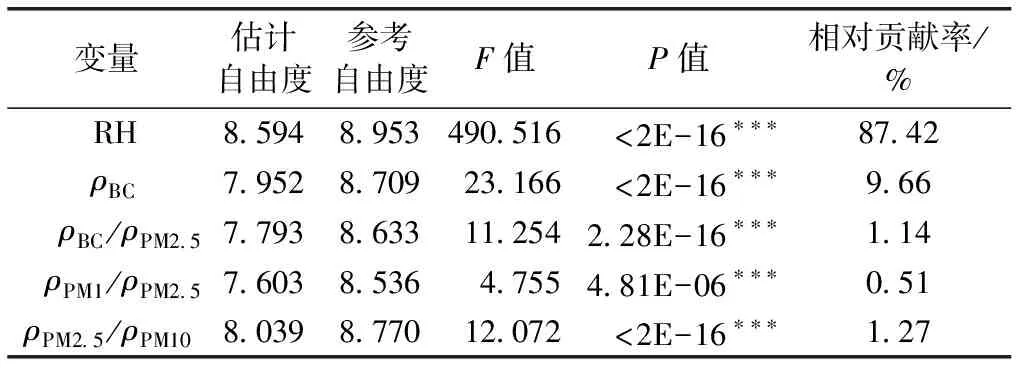
表4 气溶胶散射吸湿增长因子与5个解释变量的GAM模型的拟合结果

通过对多变量GAM模型的分析，获得解释变量的平滑回归函数，并得到各变量对气溶胶散射吸湿增长因子的影响效应图(图1)。由图1(A)可知，气溶胶散射吸湿增长因子与RH呈非线性正相关，当RH>80%时，气溶胶散射吸湿增长因子随RH增加呈快速上升趋势，这与刘新罡等[10]的研究结果一致。由图1(B)可知，气溶胶散射吸湿增长因子与ρBC呈非线性负相关，当ρBC>2.6 μg·m-3时，气溶胶散射吸湿增长因子下降趋势变缓。由于黑碳可吸附大量硫酸盐和硝酸盐，从而使气溶胶粒子尺度增加，根据凝结增长公式，粒子越大，其粒径增长过程越缓慢，这可能是气溶胶散射吸湿增长因子随ρBC升高而下降的原因。由图1(C)可知，气溶胶散射吸湿增长因子随ρBC/ρPM2.5升高呈波动下降趋势，这可能与黑碳的非吸湿性和黑碳的混合态有关[31]。由图1(D)可知，气溶胶散射吸湿增长因子随ρPM1/ρPM2.5升高总体变化较为平缓，当ρPM1/ρPM2.5>0.86时，气溶胶散射吸湿增长因子随ρPM1/ρPM2.5增加呈较明显上升趋势，反映超细颗粒物(PM1)在细颗粒物(PM2.5)中占比的升高对气溶胶散射消光的重要作用。由图1(E)可知，当ρPM2.5/ρPM10<0.75时，气溶胶散射吸湿增长因子随ρPM2.5/ρPM10增加大体呈较弱的波动下降趋势；当ρPM2.5/ρPM10>0.75时，气溶胶散射吸湿增长因子随ρPM2.5/ρPM10增加呈一定上升趋势。研究[32]表明，成都地区秋冬季PM2.5组分中有机碳(OC)、硫酸盐和硝酸盐比例明显占优，PM2.5在粗颗粒物(PM10)中占比增加会导致气溶胶吸湿性增强，这可能是气溶胶散射吸湿增长因子随ρPM2.5/ρPM10变化呈复杂形态的原因。

2.4 气溶胶散射吸湿增长因子多变量GAM模型的验证

采用R软件gam.check函数对气溶胶散射吸湿增长因子多变量GAM模型的拟合结果进行残差检验，以验证气溶胶散射吸湿增长多变量GAM模型的适用性。由图2可知，样本分位数与理论分位数(QQ图)图中点大致位于y=x直线上，且残差分布在“0”附近的频率较高，可以认为残差基本符合正态分布；另外，由散点图可见，残差分布随机，无明显趋势，模型的可信度较高。

当模型拟合值和观测值不是固定变量而是随机变量时，因变量和自变量通常不容易严格区分，而且自变量的离散性同样不能忽视。因此，在选取回归分析方法时，不应只偏重优化因变量的拟合效果，还应同时兼顾因变量和自变量的拟合偏差。压轴回归法(RMA)的优化准则是数据点与回归趋势线构成的三角形面积之和最小，该方法可同时兼顾因变量和自变量的拟合偏差。采用RMA方法评估气溶胶散射吸湿增长因子的多变量GAM模型(模型1)、基于RH的单变量GAM模型(模型2)、基于RH单变量的二次多项式模型[7](模型3)以及基于RH和ρBC的双变量参数化模型[14](模型4)的适用性(图3)。由图3可知，模型1、2、3和4的压轴回归决定系数分别为0.797、0.691、0.697和0.763，对应的平均相对误差(MRE)分别为10.04%、14.80%、15.67%和14.28%，即气溶胶散射吸湿增长因子的多变量GAM模型拟合效果最佳。进一步分析表明，模型2和模型3只考虑RH对气溶胶散射吸湿增长因子的影响，尽管两者统计方法不同，但拟合效果总体差别不大。模型4引入RH和ρBC双变量，因而气溶胶散射吸湿增长因子模拟效果显著提升。研究[15]表明，RH增加会诱发颗粒物化学组分发生变化，并导致ρPM1/ρPM2.5和ρPM2.5/ρPM10增大；另外，黑碳占比可反映黑碳外貌、混合状态和黑碳对气溶胶化学组分的影响[12,33]，模型1采用GAM模型综合考虑RH和气溶胶组分协同变化对气溶胶散射吸湿增长因子的影响，进一步降低了拟合误差，这为气溶胶散射吸湿增长因子模型构建提供了方法论。针对气溶胶散射吸湿增长因子模型在高湿条件下的不确定性，分别计算模型1、2、3和4在高RH(RH>85%)条件下的气溶胶散射吸湿增长因子，模型1、2、3和4拟合值与观测值的决定系数分别为0.684、0.524、0.538和0.637，对应的平均相对误差分别为19.76%、24.85%、24.11%和22.42%。由此可见，模型1和模型4拟合效果明显优于模型2和模型3；另外，相较于模型4，模型1进一步改善了在高RH(RH>85%)条件下气溶胶散射吸湿增长因子的模拟效果。

RH为相对湿度，ρBC为等效黑碳质量浓度，ρPM1、ρPM2.5和ρPM10分别为PM1、PM2.5和PM10质量浓度；s表示解释变量对气溶胶散射吸湿增长因子的平滑拟合值。 虚线表示拟合可加函数逐点标准差，即置信区间上、下限；实线表示解释变量对气溶胶散射吸湿增长因子的平滑拟合曲线。

图2 模型残差检验结果

模型1为多变量GAM模型，模型2为基于RH的单变量GAM模型，模型3为基于RH单变量的二次多项式模型， 模型4为基于RH和ρBC的双变量参数化模型。R2为压轴回归决定系数，MRE为平均相对误差。

3 结论

(1)采用相关性分析和方差膨胀因子相结合的方法构建了气溶胶散射吸湿增长因子的解释变量集(RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5、ρPM2.5/ρPM10)，发现气溶胶散射吸湿增长因子与RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5、ρPM2.5/ρPM10均存在显著非线性关系(均通过α=0.01的显著性检验)，其中，RH和ρBC对气溶胶散射吸湿增长因子的影响相对较大，ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10的影响相对较小。

(2)作为一种非参数统计方法，GAM模型可以很好地表征RH和气溶胶组分协同变化对气溶胶散射吸湿增长因子的影响，提供了气溶胶散射吸湿增长因子建模的方法论。

(3)基于RH、ρBC、ρBC/ρPM2.5、ρPM1/ρPM2.5和ρPM2.5/ρPM10构建的气溶胶散射吸湿增长因子多变量GAM模型能显著提升气溶胶散射吸湿增长因子的模拟效果，深化对气溶胶散射消光系数演化复杂性的认识，也为开展气溶胶辐射强迫的后续研究奠定基础。