基于ALK-MCS 算法的航空发动机轴承可靠性分析

黄洪钟，童 辉，邓智铭，钱华明，李彦锋，郭 超

(1. 电子科技大学机械与电气工程学院 成都 611731；2. 电子科技大学系统可靠性与安全性研究中心 成都 611731；3. 中国航空发动机研究院 北京 顺义区 101304；4. 重庆大学机械传动国家重点实验室 重庆 沙坪坝区 400044)

新轴承的研制需要进行可靠性试验，以验证轴承的可靠性指标是否达到规定的要求，从而为轴承的设计定型提供依据。滚动轴承可靠性的传统评价方法，是从当前批次产品中随机抽样并对样本进行可靠性试验，再依据相关标准对试验数据进行分析，进而确定当前批次轴承产品的可靠性指标。国家相关标准中规定，一般定时截尾试验失效套数不应少于轴承样品容量的2/3(最少应该保证6 套)[1]。在样本量充足的情况下，上述方法可以较为精确地对轴承的寿命与可靠性进行评估。然而，航空发动机主轴圆柱滚子轴承具有长寿命、高可靠、高成本等特点，由于研发成本、试验周期和条件等因素的制约，通常不能进行大量试验，导致无法获得足够多的可靠性数据[2]。在小样本情况下，航空发动机主轴圆柱滚子轴承的可靠性分析面临极大的挑战。

针对上述问题，文献[3]研究了在试验性能退化量有缺失的情形下的无失效小样本轴承试验，应用数据模拟方法对样本退化量进行补全，通过自助法对样本进行扩充，实现了基于性能退化轨迹方法的轴承可靠性评估。文献[4]在用自助法和Bayes方法实现小样本滚动轴承寿命分布参数估计的基础上，运用Copula 函数实现了滚动轴承在不同失效模式下竞争失效的可靠性建模，并对Copula 函数进行了参数估计。文献[5]应用Bayes 方法研究滚动轴承的可靠性，在充分利用先验信息的基础上，实现了在小样本少失效数据情形下对滚动轴承寿命的快速评估，通过实例给出了轴承序贯试验方案和判定标准。文献[6]基于无失效试验数据对滚动轴承可靠性进行了研究，在小样本无失效数据的情形下，建立了滚动轴承耐久性寿命的可靠性数学模型，给出了几种不同的可靠性评估方法。文献[7]基于长寿命轴承的性能退化数据，提出了一种小样本情形下的结合退化模型和蒙特卡洛方法的轴承可靠性评估方法，并通过实例验证了方法的有效性。文献[8]通过可靠性试验获得了某零部件的寿命数据，基于威布尔分布拟合其寿命分布类型，并对其进行了可靠性分析。文献[9]对威布尔分布参数估计和零故障数据情况开展研究，开发了一种新的参数估计方法，得到了具有较好的威布尔分布尺度参数的无偏估计量。此外，文献[10-15]还提出了一些轴承的可靠性评估方法，此处不再赘述。

尽管已有很多关于轴承的可靠性分析方法，但当轴承的功能函数未知时，目前的大部分方法都不适用。此时，如何高效地利用轴承的仿真数据进行功能函数拟合并进行可靠性计算，是当前开展轴承可靠性分析面临的严峻挑战。鉴于此，本文对航空发动机主轴圆柱滚子轴承进行有限元仿真分析，并结合Kriging 模型对轴承仿真数据进行近似建模，进一步联合主动学习Kriging 模型(active learning kriging, ALK)和 蒙 特 卡 洛 模 拟 法(Monte Carlo simulation, MCS)进行可靠度计算，形成了求解可靠度的高效高精度ALK-MCS 算法。

1 ALK-MCS 算法

1.1 Kriging 模型基本理论

Kriging 模型的本质是针对少量样本的函数插值拟合。假定根据拉丁超立方试验设计方法得到输入样本点，并基于相关试验或有限元仿真得到输出样本，具体如下：

1.2 ALK-MCS 算法

1.2.1 MCS

1.2.2 学习函数和选点规则

图1 ALK-MCS 算法流程图

2 圆柱滚子轴承有限元仿真

2.1 圆柱滚子轴承三维建模

作为高速旋转部件，滚动轴承通常对内圈、外圈与滚珠的要求较高，应具有良好的冲击韧性与耐磨性，以及较高的强度和硬度。同时，对滚动轴承的保持架要求具备良好的导热性、耐磨性、刚度和弹性。本文以某型号的航空发动机主轴轴承为对象，其内外圈和滚动体的材料采用全淬透型高碳铬轴承钢(GCr15)，保持架则通过#J 钢板冲压而成，材质为08#低碳钢板；圆柱滚子与滚道为线接触轴承。对于该圆柱滚子轴承，最终构建的三维模型如图2 所示。

图2 圆柱滚子轴承三维模型

2.2 圆柱滚子轴承有限元仿真分析

使用ABAQUS 软件对轴承进行仿真，具体步骤如下。

1) 通过SOLIDWORKS 三维建模软件与ABAQUS 有限元分析软件间的配合，实现模型装配的直接传递，将初始三维模型输入ABAQUS中。在ABAQUS 软件中，有多种单位制可供选择，如表1 所示，本实例选用SI(mm)制单位。在仿真分析模型中，材料参数设置如表2 所示。

表1 仿真软件ABAQUS 中SI 单位制

表2 有限元分析中的材料参数

2) 装配。装配时轴承的内外圈应保持同轴心，并以计算的游隙为输入，在装配界面通过圆周阵列，将滚动体等间距地装配至轴承内。

3) 网格划分。网格划分在有限元分析模型中极为重要，本实例采用C3D8 六面体进行网格划分，图3 为网格划分后的有限元分析模型。

图3 轴承仿真模型网格划分

4) 设置轴承套圈运动的边界条件。在仿真分析中，仅释放内圈沿X轴径向位移自由度，外圈完全固定。

5) 载荷条件的设定。径向载荷设置为800 N。

6) 接触条件的设定。在实际中，内外圈与滚动体之间有润滑油油膜的作用，使其并未直接接触。润滑油种类不同，其摩擦系数也不一样。选用常用Andok C 润滑油，平稳运转、寿命长，摩擦系数约为0.08。故本实例中在初始分析步设置通用接触属性，法向设定为硬接触，切向设定摩擦系数为0.08。

7) 约束条件的设定。本实例通过耦合约束控制轴承内圈内表面与外圈外表面，从而通过控制内圈内表面耦合点与外圈外表面耦合点的运动状态来约束整个轴承的运动状态。

8) 分析步设定。分析步的设定在ABAQUS 中十分重要，考虑到轴承中多种因素对应力响应的影响，本实例通过软件中显式动力学分析方法进行求解。设定总分析时长为1 s，最小增量步为0.01 s，稳定最大增量步为0.02 s，最终输出帧数为65 帧。

通过以上流程，可以得到圆柱滚子轴承的有限元仿真分析结果整体应力分布图，如图4 所示。

图4 轴承整体应力分布图

3 圆柱滚子轴承可靠性分析

对航空发动机主轴圆柱滚子轴承进行有限元仿真分析得到轴承内的最大应力。当最大应力小于材料的屈服强度时，说明圆柱滚子轴承安全可靠。然而，在工程实际中，圆柱滚子轴承受到各种不确定性因素的影响，从而造成轴承内的最大应力存在一定的波动性。鉴于此，本文将圆柱滚子轴承材料性能(摩擦系数)、载荷等参数视为随机变量，如表3所示。从而，基于抽取的随机变量样本数据改变有限元分析过程中所施加的边界条件，得到不同随机变量下的最大应力，进而进行圆柱滚子轴承可靠性分析。同时，考虑到轴承单次仿真耗时长，以及直接通过仿真应力求解可靠度时计算量大，本文引入ALK-MCS 算法来计算圆柱滚子轴承的可靠度。

表3 滚子轴承中的随机变量

采用ALK-MCS 算法对航空发动机主轴圆柱滚子轴承进行可靠性分析，具体计算结果如表4 所示，图5 为提出方法在迭代过程中对应的有限元分析得到的某一迭代点下的最大应力云图。

表4 基于ALK-MCS 算法的计算结果

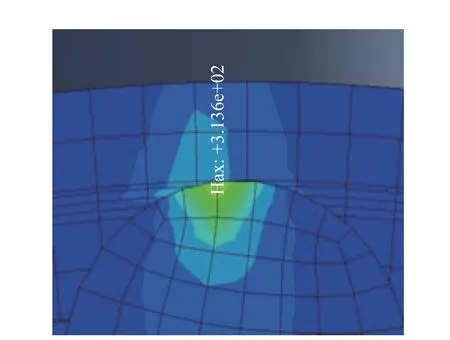
图5 滚子轴承最大应力值

从表4 可知，采用ALK-MCS 算法在迭代43次后就能得到轴承的失效概率，说明了该方法对涉及有限元仿真时的可靠性分析是有效的。同时，采用该算法最终得到轴承的失效概率为0.0002，可靠度为0.9998。需要特别指出的是，本文做一次轴承的仿真大概需要25 min，直接采用MCS 算法需要仿真2000000 次，计算成本无法接受，从而再次说明了本文提出的ALK-MCS 算法对涉及有限元仿真时的可靠性计算问题的有效性，同时由于该轴承失效寿命数据有限，通常的基于寿命分布的可靠性评估方法并不适用，本文所得结果可为决策者提供参考。

4 结 束 语

本文对航空发动机主轴圆柱滚子轴承进行了有限元仿真分析，并基于ALK-MCS 算法对轴承的可靠性进行了计算。

1)将Kriging 代理模型引入航空发动机主轴圆柱滚子轴承的可靠性分析中，提出了一种联合主动学习Kriging 和MCS 的ALK-MCS 可靠性分析方法，有效解决了MCS 方法效率低，不适用于可靠性仿真分析的问题。

2)通过SOLIDWORKS 三维建模软件建立了某型号航空发动机主轴圆柱滚子轴承的三维模型，并导入有限元仿真软件ABAQUS 中，完成相关参数设定、模型网格划分与约束加载，从而求解得到了该轴承内的最大应力，为验证提出的可靠性分析方法提供了仿真数据支撑。

3)基于ALK-MCS 算法，对某型号航空发动机主轴圆柱滚子轴承进行了可靠性分析，得出其可靠度为0.9998，验证了ALK-MCS 算法是一种高效的结构可靠度计算方法，适用于功能函数为隐函数的情形。