基于逐步回归分析的民机静压源误差修正

张 鹏，白彦辉

（中国民航大学a.适航学院；b.电子信息与自动化学院，天津 300300）

飞机在飞行过程中无法直接测得空速、气压高度等参数，获取这些重要参数要通过大气数据系统采集大气全压、静压、总温、迎角和侧滑角等数据[1-2]，再利用空气动力学原理解算出所需飞行参数[3]。 为了能够获得精确的空速、气压高度，必须保证大气数据系统测量数据的误差足够小（又因机身流场影响，静压测量值必然存在误差），因此校正静压测量误差十分必要。1998年至今，有各类静压源误差的修正方法被提出，主要包括表格插值修正法[4]、拖锥试飞校正法[5]、风洞试验校准法[6]、释放气象探空气球法[7]、大气数据系统的模糊逻辑建模法[8]及人工神经网络校准法等[9]。 以上方法中，表格插值修正法需要在大气数据计算机中存储大量表格数据，耗费存储资源；拖锥试飞校正法、风洞试验校准法及释放气象探空气球法实验成本较高、周期较长；大气数据系统的模糊逻辑建模法要求样本数据覆盖全部飞行状态，同样导致实验成本较高；人工神经网络校准法需要调整合适的网络深度和结构，并需要使用大量数据进行训练。 基于以上问题，通过逐步回归分析方法建立结构简单、计算精度高的回归方程以修正静压源误差。

采用计算流体力学（CFD，computational fluid dynamics）仿真实验方法测量静压数据，所得结果与飞行试验结果具有较强相似性，能克服飞行试验复杂实验条件的限制，且具有方便快捷、实验周期短及实验成本低的特点。文中主要针对仿真实验模型有效性验证、静压源误差变化规律及误差修正方案展开研究。

1 仿真实验模型有效性验证

有效性验证需要确定仿真实验与实际飞行数据具有较强一致性，即仿真数据有效，可用作后续误差修正实验。以B777 机型为例，根据文献[10]提供的飞机各项尺寸参数，以及波音公司发布的B777 三视图，利用Solidworks 创建飞机三维模型。 使用ICEM CFD软件在三维模型外部创建半径为20 倍机身长度的球形计算域，并对该计算域进行网格划分。

根据文献[11]，B777 飞机左右2 个主静压孔站位（STA，station）、水线（WL，water line）分别为（STA748，WL195）和（STA765，WL195），2 个备用静压孔站位、水线分别为（STA688，WL196）和（STA664，WL196），换算为以机头为原点的实验模型空间坐标系中的位置分别为左侧主静压孔（-367，-31.4）、右侧主静压孔（-358，-31.4）、左侧备用静压孔（-325，-30.5）、右侧备用静压孔（-312，-30.5）（单位：mm）。通过仿真实验确定三维模型中静压孔安装区域坐标，并与该组坐标进行对比，判断模型有效性。

在FLUENT 软件中，计算模型采用二阶迎风差分格式，基于压力、定常的3D 求解器，湍流模型选择RNG k-ε。边界条件：球形流域边界设置为自由来流边界条件[12]，假设来流为10 km 高空的理想气体，来流温度223 K，来流压强26 418 Pa。 根据文献[13]，静压孔气动布局主要影响因素是马赫数Ma 和迎角α， 据此设计两组实验计算工况： 第一组， 计算工况为Ma=0.6，α 取值范围-5°～20°，步长为5°；第二组，计算工况为α=0°，Ma 取值范围0.4～0.8，步长为0.1。 两组计算工况中侧滑角β 均为0°。

通过软件处理后结果可知，α 较大时静压在机身前部呈条带状分布，α 较小或为负值时静压在机身呈片区分布。 确定静压孔安装区域步骤如下。

（1）综合分析静压云图，框选一个大致区域，如图1 所示，由图1 可知，框选区域在α、Ma 变化时其静压偏差值小于其他区域。

图1 框选区域图示Fig.1 Selection diagram

（2）将框选区域沿水线方向分割为4 个条状面，自上而下分别以面1、2、3、4 标记。

（3）分别计算各工况下4 个条状面的静压源误差ΔP 平均值，分析平均值随Ma、α 的变化规律。

静压孔布局原则要求ΔP 随Ma 变化规律简单，对α 变化不敏感[13-14]。图2 表示ΔP 随Ma 变化情况，由图2 可知，4 个条状面ΔP 随Ma 变化规律均较为简单；图3 表示ΔP 随α 变化情况，由图3 可知，面3 静压对α 变化最不敏感。因此，仿真模型中静压孔的最佳安装位置可从面3 中选取。 该面4 个定位点坐标分别为（-280，-30），（-280，-40），（-400，-30），（-400，-40）。

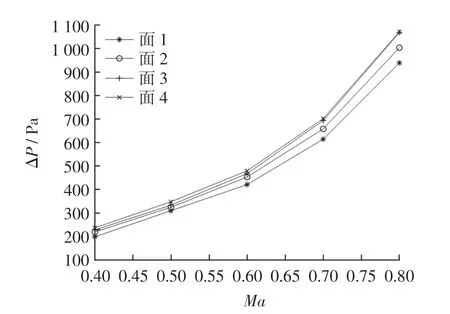
图2 静压源误差随Ma 变化情况Fig.2 Coordinate lines of static source error vs.Ma

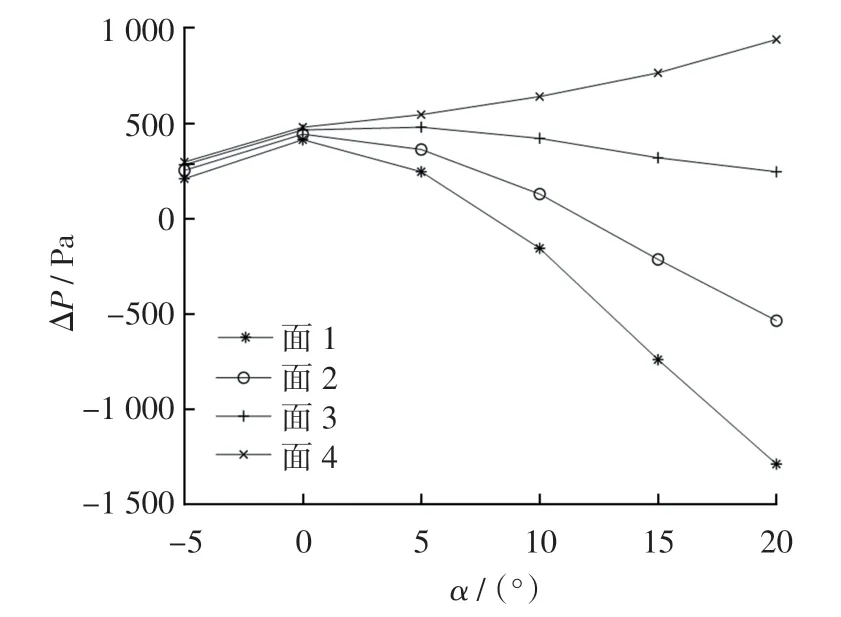
图3 静压源误差随α 变化情况Fig.3 Coordinate lines of static source error vs.α

（4）将面3 沿站位方向均分为6 段，分别计算每段ΔP 平均值随α 变化情况，如图4 所示。

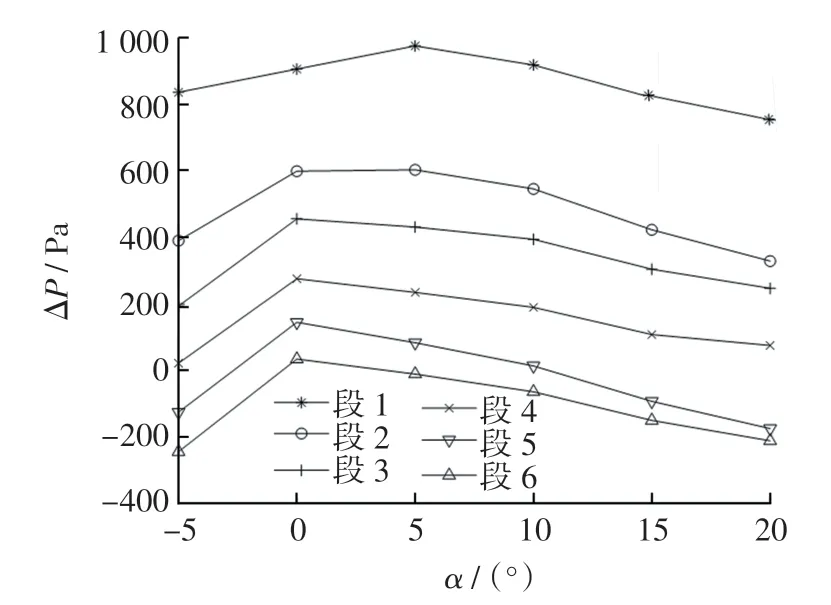
图4 各段静压源误差随α 变化情况Fig.4 Coordinate lines of static source error vs.α in each phase

由图4 可知， 在α 变化时， 第2～6 段的ΔP 相比第1 段更小，该区域更适合安装静压孔，其坐标为（-280，-30），（-280，-40），（-380，-30），（-380，-40）。

（5）重复步骤（2）～（4），进一步缩小选区，最终得到模型中静压孔适宜安装区域为（-370，30），（-370，-32.5），（-300， 30），（-300， -32.5）。该选区与实际安装区域基本重合，可认为该模型与真机具有一致性，模型有效。

2 静压源误差变化规律分析

为了研究ΔP 随Ma、α 变化情况， 并对其加以修正。 同时考虑到误差修正模型应该在一定范围的高度层中具有一定的泛化能力，故本实验计算工况选择3 个高度层10、11、12 km。 每个高度层Ma 取值范围为0.4～0.8，步长0.1，α 取值范围为-5°～20°，步长5°， β 为0°。 利用CFD-Post 软件对上述工况进行仿真实验结果导出，得到相关实验数据。

以10 km 高度层为例，绘制右侧主静压孔ΔP 随α 和Ma 的变化趋势，如图5 所示，后续误差修正均以右侧ΔP 数据为拟合目标。

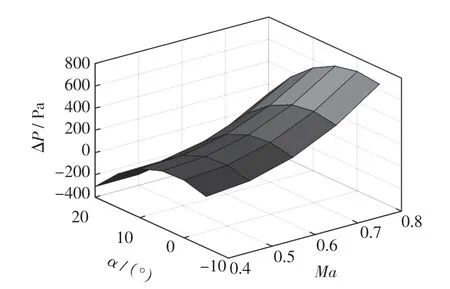
图5 10 km 高度层时静压源误差随α、Ma 变化情况Fig.5 Static source error vs.α，Ma altitude of at 10 km

表1 为当Ma 固定为0.6 时，3 个高度层的ΔP随α 的变化规律情况。 由表1 可知，3 个高度层的ΔP变化规律相似，均随α 的增大先增大后减小，最大值出现在α=0°附近。

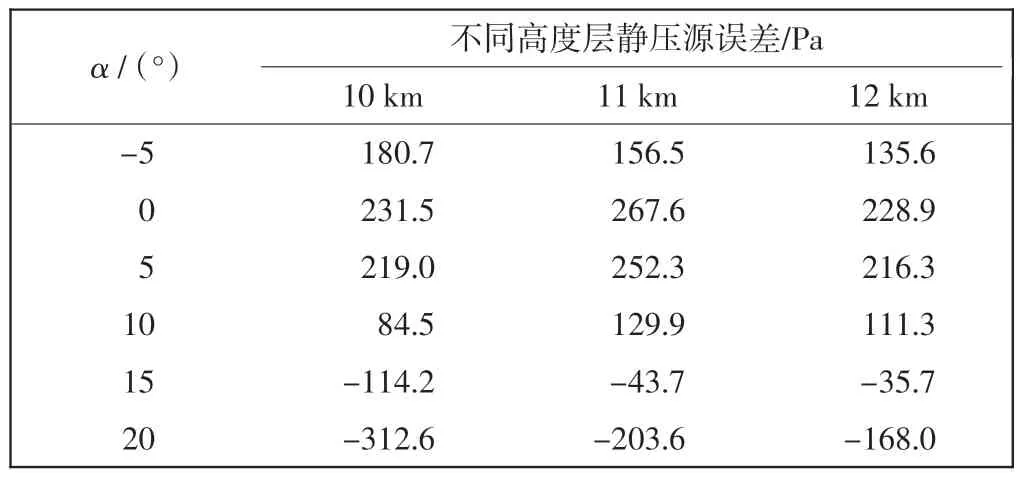
表1 不同高度层静压源误差随α 变化情况（Ma=0.6）Tab.1 Static pressure source error vs.α at different altitudes（Ma=0.6）

表2 为当α 固定为0°时，3 个高度层ΔP 随Ma 的变化情况。 由表2 可知，3 个高度层的ΔP 均随Ma 增大而增大。

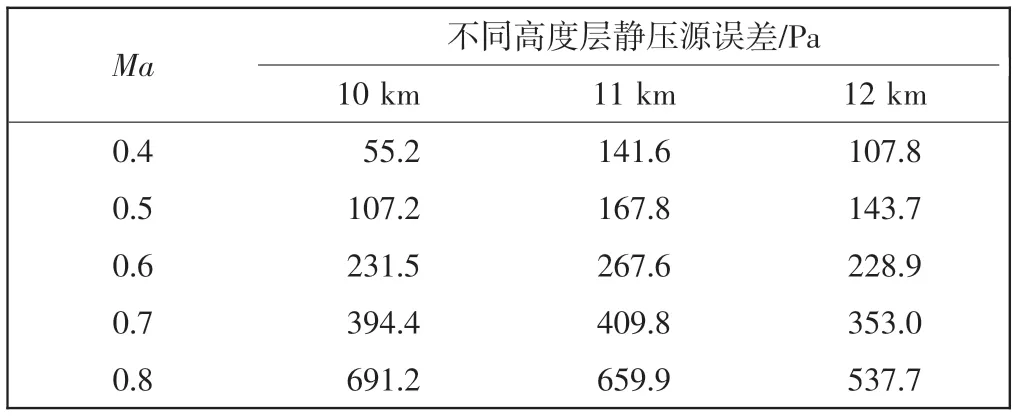
表2 不同高度层静压源误差随Ma 变化情况（α=0°）Tab.2 Static pressure source error vs.Ma at different altitudes（α=0°）

以上数据表明：不同高度层状态下，ΔP 变化规律具有相似性，后续实验可使用同一误差修正方案来校正多工况下的ΔP。

3 误差修正方案

3.1 逐步回归分析

逐步回归分析用于建立最优或合适的多元回归模型，能够较为深入地研究变量之间的依赖关系，且逐步回归分析所得的回归方程变量较少，并保留了影响最显著的重要变量，预测精确度较高[15]，可有效规避计算复杂度高的问题。

3 种常用逐步回归分析如下。

1）前向选择

将自变量逐个引入模型，若当前引入的自变量使模型发生显著性变化，则将该变量保留在模型中，否则忽略该变量，直至遍历所有变量。

2）后向剔除

将所有变量放入模型，逐个剔除，若剔除当前自变量后模型发生显著性变化，则保留该变量，否则确定剔除，直到留下所有对模型有显著性变化的因素。

3）双向剔除

在引入一个变量后，对整个模型中的所有变量进行检验，剔除作用不显著的变量，直到回归方程仅包含显著性解释变量，得到一个最优的变量集合。

3.2 回归方程建立

建立单一回归方程，校正不同高度层下的ΔP，则回归方程的自变量应包含α、Ma 和气压高度H，因在ΔP得到校正前H 无法直接获得，又知全压Pq隐含空速V 和H 的信息，故使用全压Pq间接表征H，并结合α 和Ma参与计算。利用80%的实验数据，通过逐步回归分析，由低阶向高阶逐步分析α、Ma、Pq对ΔP 的影响程度，并根据逐步回归分析所计算出统计学信息R2、F、p 及回归方程系数，确定并建立表征相关关系的最简回归方程。

统计学信息中，R2是回归方程的方差解释能力，R2越接近1，回归方程的方差解释能力越强，表示如下

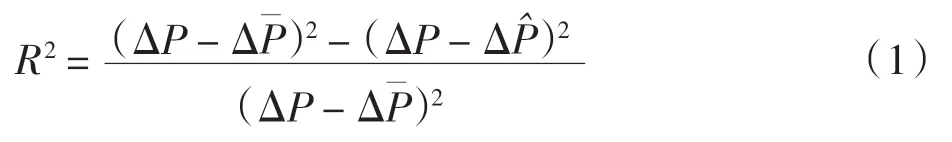
一阶回归方程共有7 种实现形式，进行双向剔除逐步回归分析实验，并记录相关信息于表3 中。

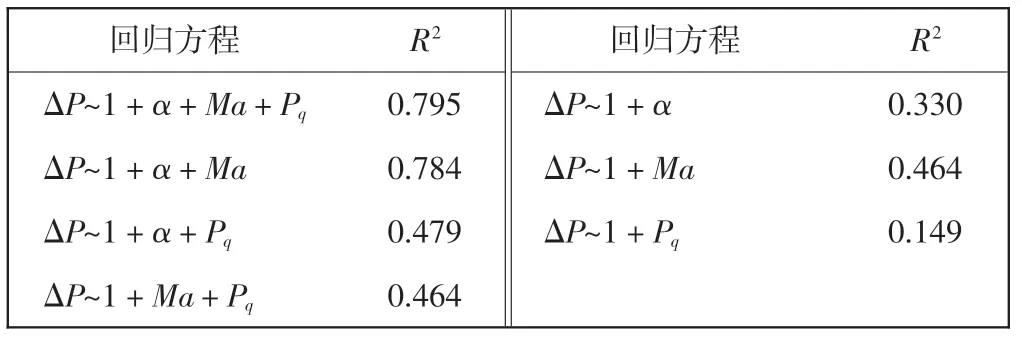
表3 一阶回归方程及R2 值Tab.3 First-order regression equation and R2 value

由表3 可知，7 组一阶回归方程均无足够的方差解释能力， 其中回归方程ΔP～1+α+Ma+Pq的方差解释能力优于其他回归方程。 进而在该回归方程基础上考虑二阶回归方程形式，使用后向剔除将所有变量均引入方程，逐一剔除，并观察模型显著变化情况，得到R2最大的回归方程形式为

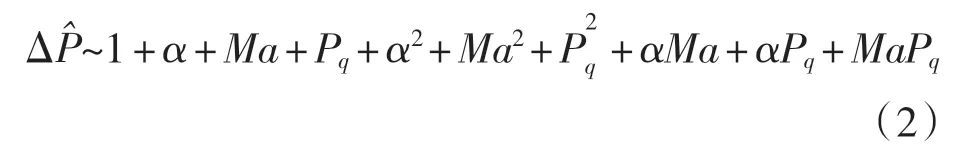
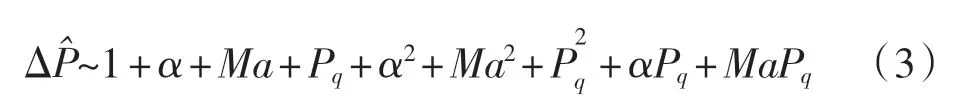
回归方程的统计信息如表4 所示。

表4 二阶回归方程的统计学信息Tab.4 Statistical information of the second-order regression equation

由表4 知，两组回归方程都已具有足够的方差解释能力，对比其余两项参数可知，式（3）相比式（2）具有更好的拟合能力和更高的可信度，因此选用式（3）作为静压源误差回归方程的最终形式，将逐步回归分析所估计的回归方程系数代入式（3）得到

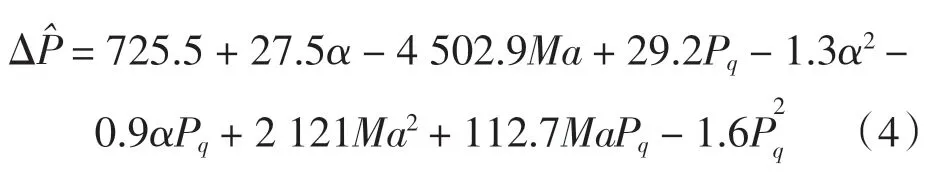
利用未参与逐步回归分析实验的剩余20%实验数据分析该模型误差校正后残差分布情况，回归模型残差如图6 所示。 由图6 可知，回归模型校正后的残差分布具有随机性。 残差的正态概率分布如图7 所示。

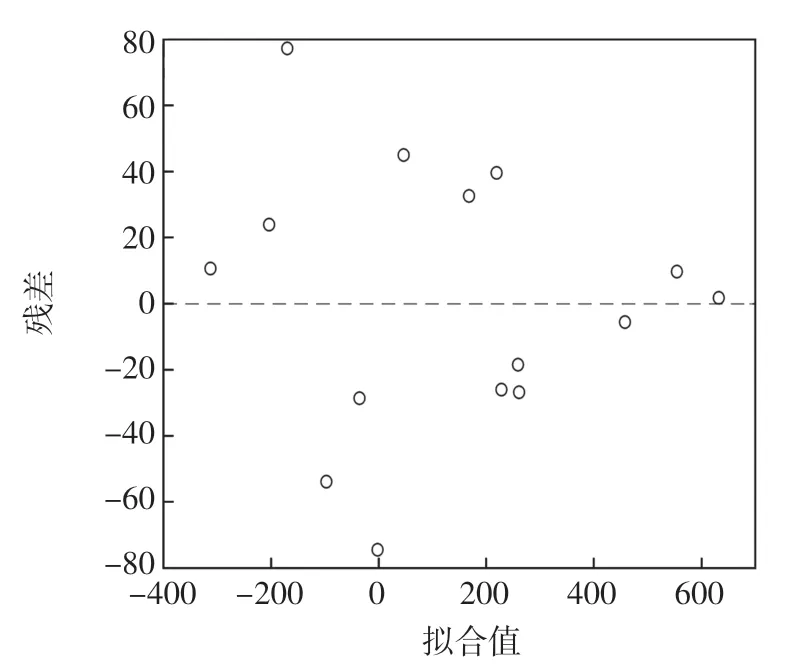
图6 回归模型残差图Fig.6 Residual plot of regression model

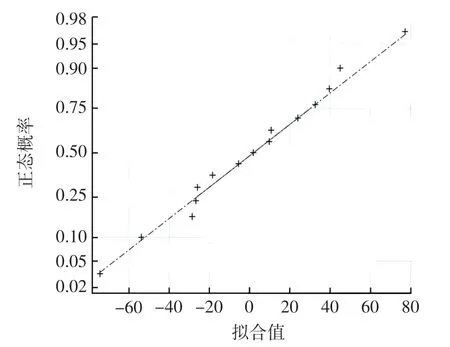
图7 残差正态概率分布Fig.7 Normal probability distribution of residual

由图7 可知，残差分布基本呈直线分布，服从正态分布。

综上可知，该回归模型具有合理性，模型的实际校正效果还需从误差方面进一步分析。

4 修正方案有效性验证

以11 km 高度层处α=0°时不同Ma 对应的ΔP 修正结果为例， 分析使用逐步回归模型修正误差的效果。如表5 所示，该高度层自由来流静压为22 700 Pa，可见测量误差已得到修正，保持在0.2%以下。 使用校正后的静压来解算空速，结果如表6 所示，解算所得的校准空速误差小于3%。经验证回归方程在修正10、12 km 高度层处ΔP 同样具有较好的误差修正能力，校准空速误差均小于3%，符合适航条款要求[16]，因此该修正方案有效。

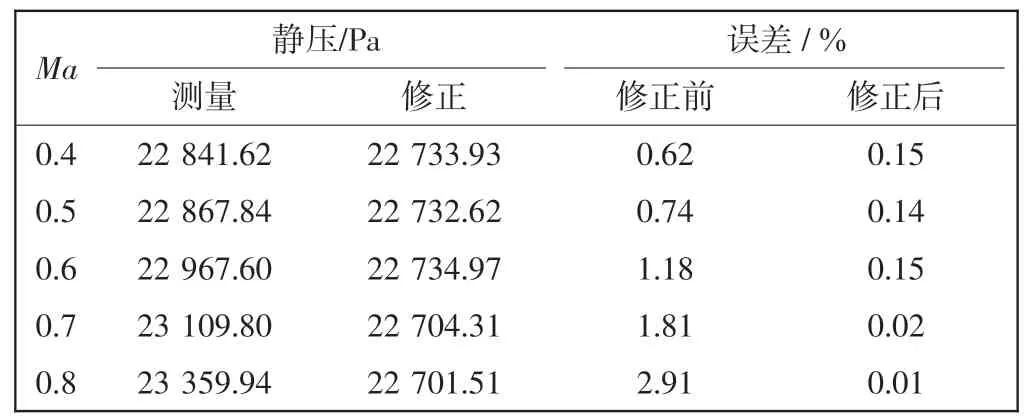
表5 11 km 高度层处不同Ma 的静压源误差修正结果（α=0°）Tab.5 Static pressure corrected by regression model with different Ma at 11 km altitude（α=0°）

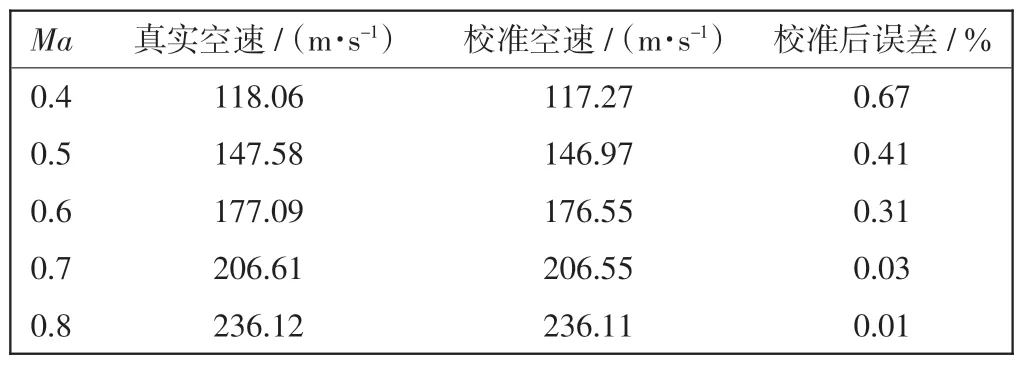
表6 校准空速及校准后误差Tab.6 Calibration airspeed and error after calibration

5 结语

在采用仿真建模方法确定模型静压孔布局有效的前提下进行一系列误差修正实验，根据实验结果得出如下结论。

（1）在尝试使用更高阶回归方程拟合误差时，通过实验结果随阶数增高而变差可知，在回归实验中不能盲目追求高阶数，追求高阶数可能无法保证结果准确性，同时也会耗费计算资源。

（2）该误差修正方案克服了表格插值修正法需要存储大量数据及人工神经网络模型需要复杂训练过程等不足。

（3）使用逐步回归分析校正静压源误差，校正后的残差分布具有随机性，残差正态概率符合正态分布，证实误差修正方案具有合理性。通过校正后的静压解算的空速误差均小于3%，符合适航条款要求，证实误差修正方案的有效性。故该方案可为民机静压源误差修正余度设计提供一定的参考。

在后续的研究中，可尝试进一步考虑侧滑角的影响，对爬升、下降阶段进行仿真及误差分析与修正研究，完善误差修正方案，进而在飞行的全阶段修正静压源误差。