“保险+期货”的套期保值比率和绩效评估研究——以黄玉米为例

姚定俊，张 路，程恭品

（1.南京财经大学 金融学院，江苏 南京 210023；2.南京财经大学 经济学院，江苏 南京 210023）

一、引言

“保险+期货”是指农业经营者或企业为规避市场价格风险向保险公司购买期货价格保险产品，然后保险公司通过向期货经营机构购买场外期权将风险转移，期货经营机构再利用期货市场进行风险对冲的业务模式。自2015 年大连商品交易所首倡“保险+期货”项目以来，该模式已连续六年写入中央“一号文件”。2021年出台的《中共中央国务院关于全面推进乡村振兴加快农业农村现代化的意见》明确提出，要发挥“保险+期货”在服务乡村产业发展中的作用。截至2021年6月，“保险+期货”试点工作已累计开展930 多个项目，涉及27 个省份、459 个县，扩展到14个品种，现货量接近1400万吨，服务农户141万户，实现赔付超过13亿元。目前，“保险+期货”模式正在推进产业风险保障向更宽领域、更深层次延伸和拓展。当前我国“保险+期货”的实际运作模式如图1 所示，是由保险公司、期货公司的资管子公司或投资子公司、养殖户、政府、交易所、银行等多个主体共同构成的完整网络链条。“保险+期货”在现行运营模式下，可使保险公司、期货公司和农户等多方获利，实现互惠共赢，其主要优势包括如下几个方面。

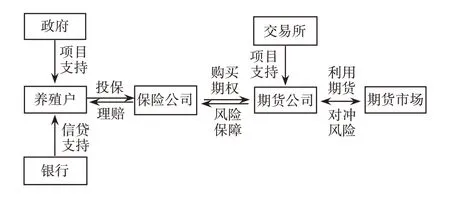
图1 “保险+期货”运作模式示意图

第一，“保险+期货”模式帮助保险公司分散了原来农业保险难以化解的巨灾风险，提高了保险公司的风险管理能力，是除再保险之外的另一种风险转移方式，丰富了风险管理工具，为我国保险行业健康运转提供了有力保障。

第二，政府可以通过补贴保费的方式替代农业直接补贴政策，有利于粮食战略储备和农业增产增收。由于补贴保费的成本低于临储政策和农业直接补贴政策的财政支出，减轻了政府财政的负担。“保险+期货”模式把风险转化到资本市场，比原来的直接转移支付的政策更高效；同时也规避了国际市场对农业直接补贴的限制。

第三，保险公司可利用其分支网点分布广泛的优势，将农业保险市场做大做强。“保险+期货”体量的扩大可以有效促进期货公司业务量的增大，有利于期货公司的经纪业务发展，有利于提高期货市场上机构投资者的权重占比，从而在有效性、流动性和规范性等方面促进我国期货市场的可持续健康发展。

第四，虽然农业生产单位可通过金融衍生品市场进行套期保值，但是我国的农业生产单位大多由家庭构成，生产规模较小，产量未必能达到期货一手的最低限；同时，金融衍生品市场对投资者存在文化水平、专业技术等较高的隐性门槛，因此绝大多数农户难以直接参与金融衍生品市场。而“保险+期货”模式可以直接通过保险销售来服务广大农户，大大降低了技术壁垒和参与门槛，可以让农户轻松享受到金融衍生品市场带来的服务。

我国金融实务的快速发展亟须理论研究的配套支撑，部分学者已经开始了“保险+期货”领域的研究。通过知网查询可知，截至2022年1月底，标题含“保险+期货”的中文论文共315篇，其中绝大多数文献研究集中在定性分析上，而定量研究的文献仅5篇左右。定性研究的文献主要关注我国现有“保险+期货”试点项目的运行机制优化以及相关经验借鉴。董婉璐等（2014）[1]以美国玉米产业为例，分析了农业保险和农产品期货对农民收入的保障作用，为我国提供了经验借鉴。李正强（2015）[2]在分析大连商品交易所“保底租地协议+场外期权+期货”新模式的基础上，提出了加大政策扶持力度，为新型涉农主体管理价格波动风险提供财政补贴，支持试点推广等建议。李亚茹和孙蓉（2017）[3]认为期货价格保险是大宗农产品和鲜活农产品价格调控的重要市场化工具，提出了增加农产品期货品种、建立再保险体系等建议。

定量研究的文献极少，可以分为两种类型。

一类是分析“保险+期货”试点产生的相关影响。如方蕊等（2019）[4]研究了试点与我国现有农业补贴政策的影响关系，张子健等（2021）[5]研究了试点对农户农资投入和经营规模的影响，潘方卉等（2022）[6]研究了饲料成本“保险+期货”模式对猪肉市场价格波动的影响。

另一类是从技术层面研究精准定价问题。如吴开兵等（2021）[7]从保险公司的视角出发对“保险+期货”中的定价问题展开了讨论。迄今为止，在“保险+期货”框架下，从我国保险公司角度出发对分散承保风险的研究几乎还是空白。基于上述背景，本文以黄玉米为例，在“保险+期货”的框架下尝试为保险公司探索最优的套期保值比率，以达到最大限度分散保险公司承保风险的目的。该问题研究可为“保险+期货”项目未来的健康发展提供参考。

（一）研究方法

在套期保值研究方面，我们发现随着经典方法到静态套期保值方法再到动态套期保值方法的演变，虽然模型越来越复杂，在不少品种上也取得了一些优化效果，但是在农产品的相关研究中，套期保值绩效仍然偏低，且套期保值绩效指标值最高的仍是经典的OLS模型。Alexander和Barbosa（2007）[8]很早就指出，在成熟活跃的市场中，没有任何证据可以证明后来这些更加复杂的计量模型比OLS模型估计的套期保值比率更加有效，过分追求复杂模型可能背离了研究服务于市场的初心。近年来伴随着我国金融市场的整体发展，无论是保险行业还是期货行业都取得了长足的发展，采用何种恰当的估计模型处理最新的市场数据，以达到套期保值绩效最大化的目标，是本文重点关注的内容之一。

本文对于“保险+期货”的研究分为三个阶段。

首先，采用传统的OLS模型研究套期保值比率。由于OLS 模型没有解决残差自相关问题，继而使用能够克服该缺点的B-VAR 模型再次估算套期保值比率。但协整关系仍未被考虑，从而忽略了协整关系会使套期保值比率过低继而影响套期保值效果。

其次，考虑期货、现货价格的协整关系再使用ECM 模型进行估计，加入期货价格时间序列的异方差性，使用GARCH模型进行估计。

再次，使用复合的ECM-GARCH 模型再次估计，以获得实际效果最佳的套期保值比率。

1.传统回归的套期保值模型（OLS）

OLS 模型是最常用的传统回归模型，Witt 等（1987）[9]最早用它估计方差最小的套期保值比率。他们将期货价格和现货价格的增量分别当作解释变量和被解释变量，再做OLS的一元线性回归，即：

其中St是黄玉米在t 时刻的现货价格，ΔSt=St-St-1是它在t 时刻的现货收益；Ft是黄玉米在t 时刻的期货价格，ΔFt=Ft-Ft-1是它在t 时刻的期货收益；εt是OLS 的随机扰动项，α 是OLS 回归方程的截距项，β1是OLS 回归方程的斜率项，它刚好就是最小收益方差目标下的套期保值比率h，即：

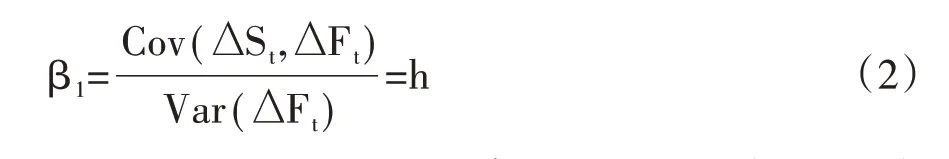
2.双变量向量自回归的套期保值模型（B-VAR）

Herbst 等（1989）[10]及Myers 和Thompson（1989）[11]在使用OLS模型研究最优套期保值比率时发现了残差自相关问题，以及解释变量过少而导致信息量受损的风险，并提供了使用B-VAR模型估计最优套期保值比率的方法。B-VAR 模型包含了两个变量，这两个变量的当前数据同时受到历史数据的影响，它们丰富了模型的信息量，也克服了残差自相关问题。

此外，B-VAR 模型的前提假设较少，适用性更强。在B-VAR 模型下，黄玉米期货市场收益率与现货市场收益率之间影响关系的表达式为：

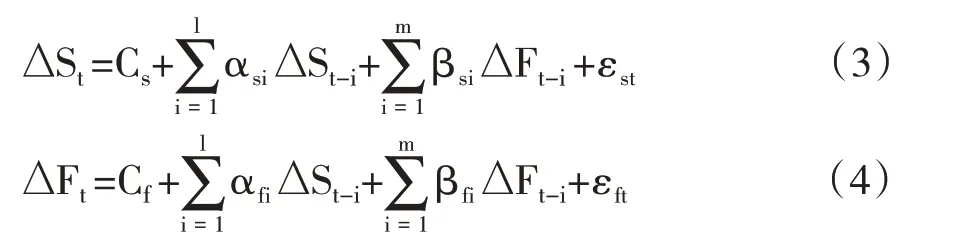
其中，Cs、Cf分别为B-VAR 模型回归方程各个对应变量的截距项，αsi、βsi、αfi、βfi分别为B-VAR 模型回归方程各个对应变量的回归系数，εst、εft分别为B-VAR 模型回归方程各个对应变量的随机扰动项，且独立同分布。

该模型进行实证研究时，首先要确定可以消除残差自相关关系的最优滞后阶数，将现货收益率序列的方差记为Var(εst)=σss，将期货收益率序列的方差记为Var(εft)=σff，将期货市场和现货市场价格收益率序列的协方差记为Var(εst,εft)=σsf，这样就得到方差最小时的套期保值比率h，表达式为：

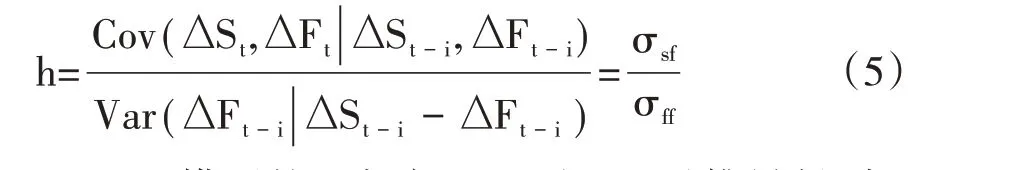
B-VAR模型的回归方程还可以通过推导得到：

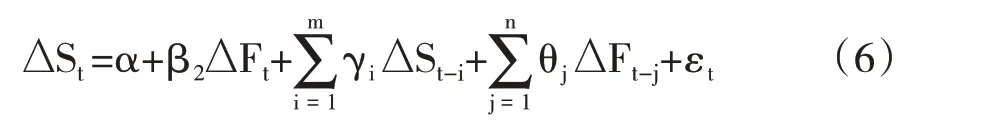
方差最小化目标下的套期保值比率h 就是式（6）中ΔFt项的系数β2。

与OLS 模型相比，B-VAR 模型的优势在于可以处理期货、现货市场收益率残差序列自相关的问题。但是美中不足的是，期货市场和现货市场价格序列可能内含协整关系及长期均衡关系，但B-VAR模型没有考虑这种可能，也没有考虑异方差性对套期保值比率产生动态影响的可能性。

3.误差修正的套期保值模型（ECM）

Granger 和Engle（1987）[12]在研究发现OLS 模型和B-VAR 模型的缺陷后，提出协整关系的概念，并丰富发展为协整理论。该理论同时包含了时间序列的解释变量和被解释变量之间的短期动态关系与长期均衡关系两个方面。他们指出，即使时间序列是不平稳的，但是仍然有可能存在一种线性组合通过平稳性检验，此时就称原序列具有协整关系，具有协整关系的变量之间可以用一个误差修正项Zt-1来表示。这样处理后，可以发现变量间潜在的长期均衡关系，既丰富了回归模型的信息，同时也解决了残差自相关问题。

Ghosh（1993）[13]首次利用ECM 模型来研究方差最小时的套期保值比率。该研究首先对期货市场价格和现货市场价格进行OLS回归；然后将基差，即期货、现货价格之差记为误差修正项；最后进行ECM模型回归。

ECM模型的表达式为：

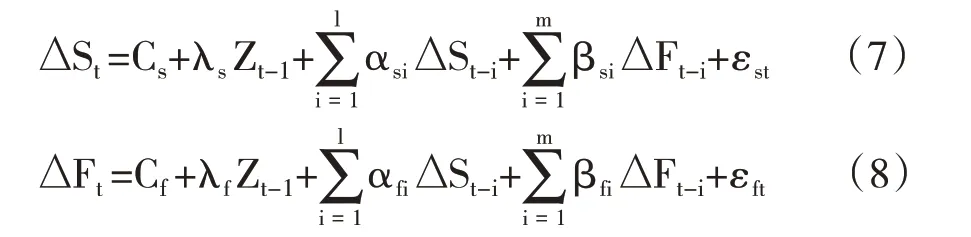
其中，Cs、Cf分别为ECM模型回归方程各个对应变量的截距项，αsi、βsi、αfi、βfi分别为ECM 模型回归方程各个对应变量的回归系数，εst、εft分别为ECM模型回归方程各个对应变量的随机扰动项，且独立同分布，Zt-1为误差修正项，λs和λf至少有一个不等于零。

通过推导，ECM模型的回归方程还可以导出：

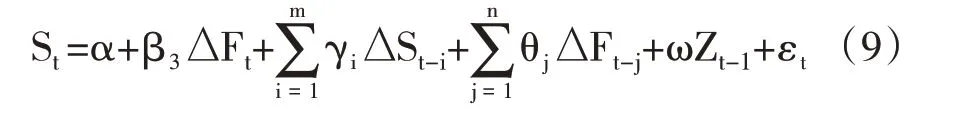
方差最小化目标下的套期保值比率h 就是式（9）中ΔFt项的系数β3。

学者们通过大量的实证研究发现，在成熟市场中可以用基差近似Zt-1，即用期货价格与现货价格之差Bt-1=Ft-1-St-1代替。但是由于我国金融衍生品市场的成熟性、规范性和有效性较成熟市场仍存在差距，直接以基差作为近似值并不可靠，所以本文采用残差项的一阶滞后项来替代Zt-1。

4.误差修正GARCH 的套期保值模型（ECMGARCH）

Cecchetti 和Figlewski（1988）[14]使用ARCH 模型估计了联邦国债期货的最优套期保值比率，指出国债期货的套期保值比率并非定值，而是动态数值。Baillie 和Myers（1991）[15]最先使用GARCH 模型研究了美国的玉米和大豆期货、现货市场的套期保值比率。Lien 等（2002）[16]发现，GARCH 模型虽然考虑了动态性，但未考虑协整关系，套期保值比率的估计值偏小，套期保值绩效明显下降，而加入修正误差项后的ECM-GARCH 模型套期保值效果更好。该模型放宽了期货、现货价格各自变化量的条件方差以及它们之间的条件协方差为定值的要求，加入了期货、现货市场价格变化的协整关系和波动率之间的联动关系。此时ECM-GARCH（1,1）模型的表达式可以通过式（7）和式（8）进一步推导得到，即：

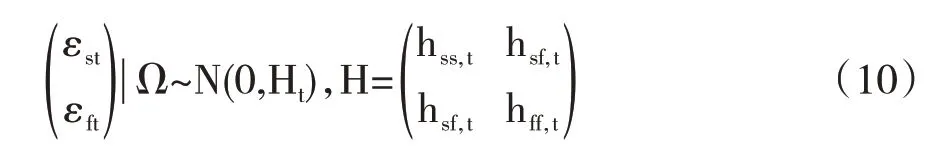
其中，hss为GARCH 模型回归后的均值方程中现货序列对应的残差项εst的条件方差，hff为GARCH模型回归后的均值方程中期货序列对应的残差项εft的条件方差，而hsj为GARCH 模型回归后的均值方程中期货、现货序列对应的残差项εst和εft的条件协方差。

根据Bollerslev 等（1988）[17]研究时推导出的简化模型，可将表达式简化为：

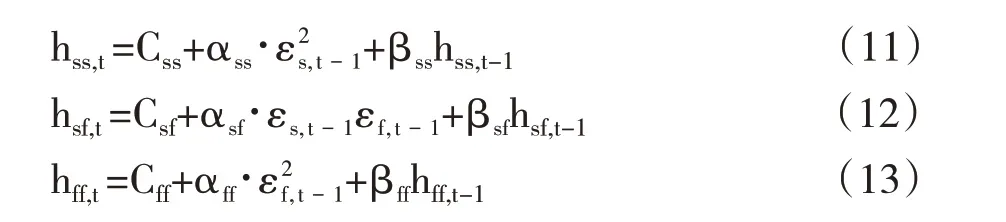
此时，现货序列的条件方差hss只受到自己的误差项εs,t-1与滞后项的影响，期货序列的条件方差hff同样只受到自己的误差项εf,t-1与滞后项的影响，而期货、现货序列的条件协方差hsf同时受误差项εs,t-1和εf,t-1以及滞后项的影响。ECM-GARCH 模型下收益方差最小化时的套期保值比率为：

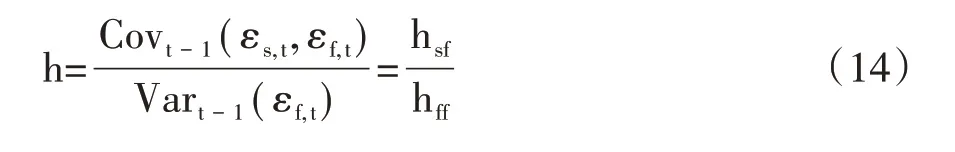
（二）黄玉米“保险+期货”绩效评估的指标

参与套期保值的收益为Ht=ΔSt-hΔFt，其对应的方差表达式为：

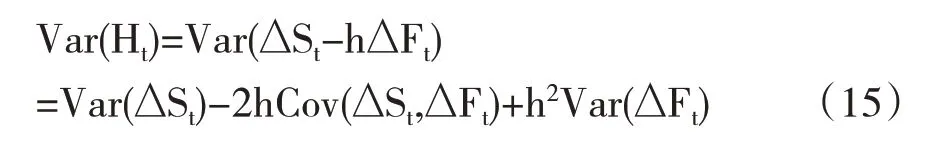
而未参与套期保值的收益相对更简单，就是现货市场的收益，即Ut=ΔSt，其对应的方差表达式为：

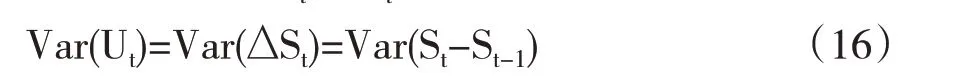
按照Ederington（1979）[18]，可以将参与套期保值前后收益方差的降低程度H 作为指标，衡量套期保值的绩效。H的计算公式如式（17）所示：

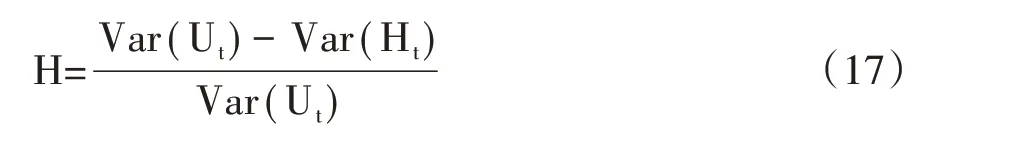
本文首先在上述5 个模型下分别计算套期保值比率h，以及对应的套期保值绩效H。然后选出最大的H 值，以及对应的套期保值比率h，此即为在“保险+期货”模式下应采用的最优套期保值比率，它对保险公司的风险保障效果最高。为了使结果更加可信，本文在对样本区间内时间序列进行套期保值绩效的计算和比较后，选出最优的套期保值比率，然后应用在样本区间外数据上进行套期保值效果检测，对比论证。

二、样本选取及处理

本文选取的数据来源于Wind 数据库，是2015年1 月5 日至2020 年2 月28 日的黄玉米期货和现货的价格时间序列，其中又以2019 年1 月1 日为界，分为样本区间内数据和样本区间外数据，合计1223 组日度数据、267 组周度数据、62 组月度数据。其中，样本区间内952 组日度数据、206 组周度数据、48 组月度数据；样本区间外271组日度数据、61组周度数据、14 组月度数据。使用样本区间内数据来估计套期保值比率，在实证分析中对2015 年1 月5 日至2018 年12 月28 日的样本进行套期保值比率估计的实证研究，对2019 年1 月2 日至2020 年2 月28 日的样本进行套期保值绩效评估的实证研究。

在选取黄玉米期货合约时，考虑到期货合约价格与股市价格等市场价格最大的差异之一就是不连续，即期货合约都有到期日，到了交割月时必须选择平仓或是实物交割，无法长期连续持有，所以本文不能像其他市场的研究方法那样直接获得连续数据。以大连商品交易所的黄玉米期货合约为例，每年有1 月、3 月、5 月、7 月、9 月、11 月交割的六个合约；除此之外，期货合约还有一个特别之处，即在同一个交易日当中，会存在多个不同交割月的期货合约同时交易。可以归纳为，同一交易日内的同一期货品种会并存多个不同交割月的期货合约。为了获取便于实证研究的连续时间序列，把即将交割、距离现在时间最短的期货合约作为基准，一旦其进入交割月份，就更换至下一个时间最短的交割月期货合约。以此类推，将这些期货市场黄玉米收盘价的价格时间序列数据汇总即可获得可供实证研究的连续时间序列数据。而在选取黄玉米现货合约时，选取中华粮网公布的含水分14%的三级黄玉米现货报价。需要特别说明的一点是：节假日等原因导致了一些没有开盘的日期，这些日期的数据将被剔除处理。

（一）描述性统计量分析

在2015年1月5日至2020年2月28日时间段以内，为了方便对比分析，服务下文的计量模型，对日度、周度、月度数据及其一阶差分的序列，还有期货、现货市场对应的对数收益率进行描述性统计量分析。

根据输出结果可知：日度、周度、月度数据及其一阶差分和对数收益率的序列在平均值、中位数、最大值、最小值、标准差、偏度和峰度所对应的几组数值较为接近，说明对应的二者之间应该存在着一定的函数映射关系，存在协同性的可能。

再看各列的J-B统计量及其对应的p值，日度数据和周度数据的J-B 统计量都远大于11，且所对应的p 值都近似为0，说明这些时间序列的正态性不足，都不服从正态分布。日度数据、周度数据、月度数据序列的偏度都大于0，所以是右偏的；而日度数据、周度数据、月度数据序列的一阶差分序列和对数收益率序列的偏度都是小于0 的，结果是左偏的。日度数据、周度数据序列的峰度都小于3，所以密度函数图像较为平坦；而日度数据、周度数据序列的一阶差分序列和对数收益率的序列的峰度都大于3，所以密度函数图像较为尖耸。

为了检验是否可以通过套期保值降低风险，对日度数据、周度数据、月度数据序列分别进行相关系数矩阵的运算。结果显示，日度数据、周度数据、月度数据序列的相关系数矩阵的相关性分别是0.959176、0.958757、0.954617，都在0.95 以上。这说明二者之间的相关性很大，所以理论上可以通过套期保值组合的方式来降低风险。

（二）数据样本的单位根检验

如果时间序列存在单位根的话，就会使得回归结果产生伪回归的情况，所以需要通过单位根检验来判断时间序列数据是否平稳。综合考虑后，本文分别对日度数据、周度数据、月度数据的期货、现货价格序列及其各自对应的一阶差分序列进行了完整的ADF检验，如表1所示。

表1 的结果显示：日度数据、周度数据、月度数据的原始价格序列的t 值在5%的显著性水平下都不能拒绝原假设，所以不能排除单位根存在的可能性。基于此，选取的日度数据、周度数据、月度数据的原始价格序列都不平稳；日度数据、周度数据、月度数据的一阶差分序列的t 值在5%的显著性水平下都能够拒绝原假设，可以排除单位根存在的可能性，认为不存在单位根。因此，选取的日度数据、周度数据、月度数据的一阶差分序列都通过了平稳性检验，都是I(1)过程。

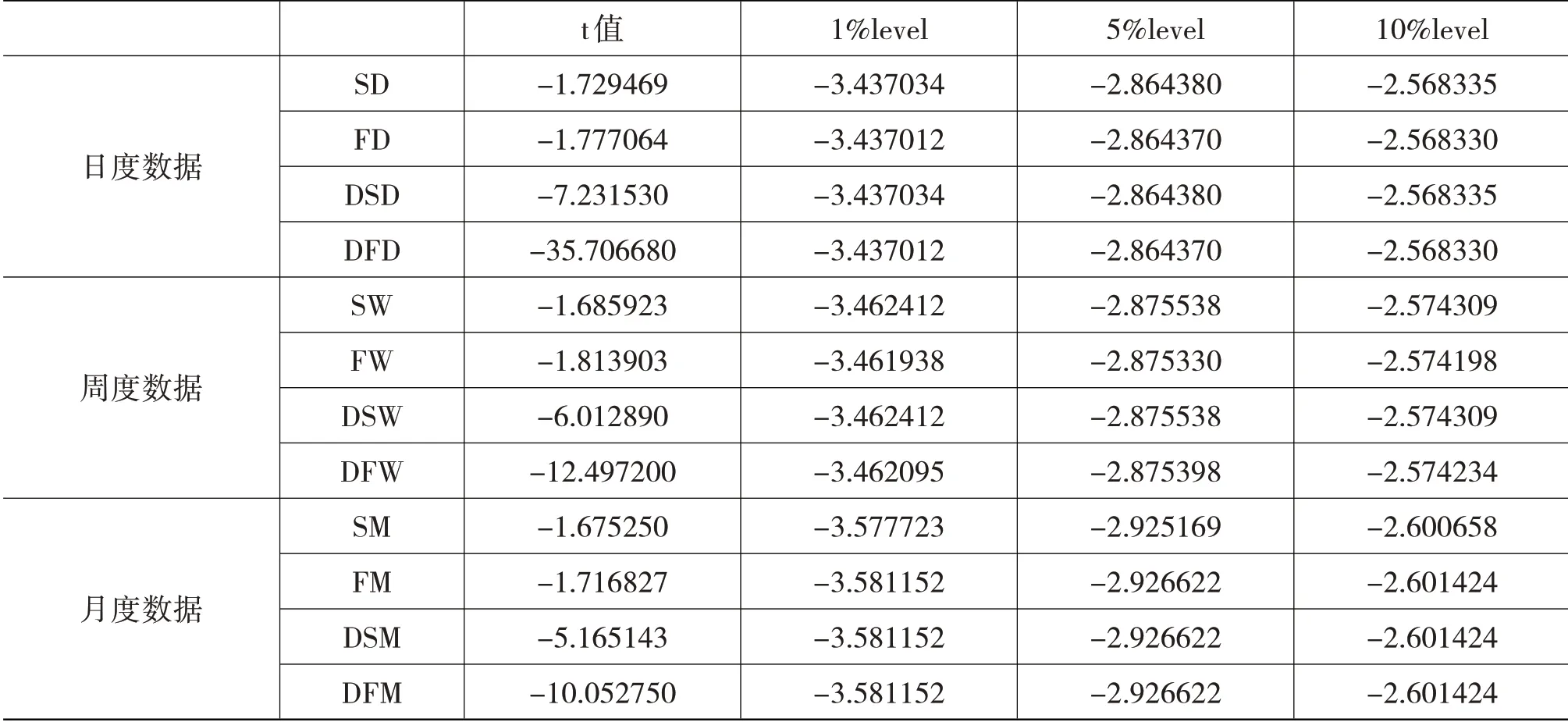
表1 单位根检验结果

（三）协整性检验

在进行ECM 的研究之前，我们需要对黄玉米现货价格和期货价格数据做协整性检验，协整向量需要满足的一个前提是解释变量和被解释变量需要相同的单整阶数。先对现货价格和期货价格的数据进行回归得到函数方程，产生残差序列ETD、ETW、ETM，进而对这些序列进行平稳性检验。若残差序列ETD、ETW、ETM 可以通过平稳性检验，则说明不存在单位根，表明变量间存在长期均衡的函数方程，该方程所代表的就是解释变量和被解释变量之间的协整关系。在前文中，我们已经知道黄玉米现货价格和期货价格的日度数据、周度数据、月度数据均为一阶单整序列，都是I(1)过程，满足协整检验的前提，可以对黄玉米现货价格和期货价格的日度数据回归方程产生的残差序列ETD、ETW、ETM 进行单位根检验。本文协整检验采用的方法是E-G 两步法，结果见表2。

表2 协整性检验结果

三、套期保值的实证研究

（一）套期保值比率估计

根据上文中给出的方法和相关数据进行实证研究，我们将所有模型估计得到的套期保值比率h 的数值汇总于表3。

表3 的结果如下：日度数据下，GARCH 模型得到的h值0.015889最小，ECM模型所得的h值0.041390最大，中间是OLS 模型所得的h 值0.034873；周度数据下，GARCH 模型得到的h 值0.040672 最小，ECM模型所得的h 值0.150323 最大，中间是OLS 模型所得的h值0.130476；月度数据下，GARCH模型得到的h值0.248685最小，而B-VAR模型所得的h值0.368315最大，中间是ECM模型所得的h值0.359604。

表3 套期保值比率h结果

结果表明：在三种不同时间间隔的数据下，GARCH模型所得到的套期保值比率始终最小；日度数据和周度数据下，ECM 模型所得的套期保值比率最大；月度数据下，ECM 模型所得的套期保值比率是第二大的。这很可能是由于自回归条件异方差对套期保值比率的影响较小，而充分考虑了期货、现货价格时间序列之间的协整关系的误差修正项的ECM 模型以及ECM-GARCH 模型的结果都非常出色。

另外，所有模型下，随着数据时间间隔从日度、周度再到月度的逐步增大，套期保值比率也同步增大。换言之，随着套期保值操作间隔时间的拉长，套期保值操作的效果越来越好，更有必要进行套期保值；同时也证明了套期保值比率与收益变动的增量之间存在负相关关系。

（二）套期保值绩效计算

如表4 和表5 所示，可根据表3 以及式（15）—式（17）计算出样本区间内和样本区间外的套期保值绩效h值。

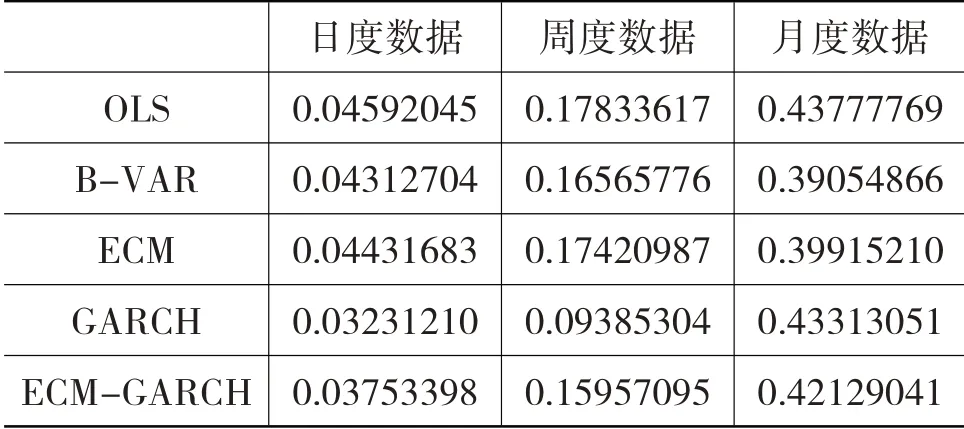
表4 样本区间内的套期保值绩效h值

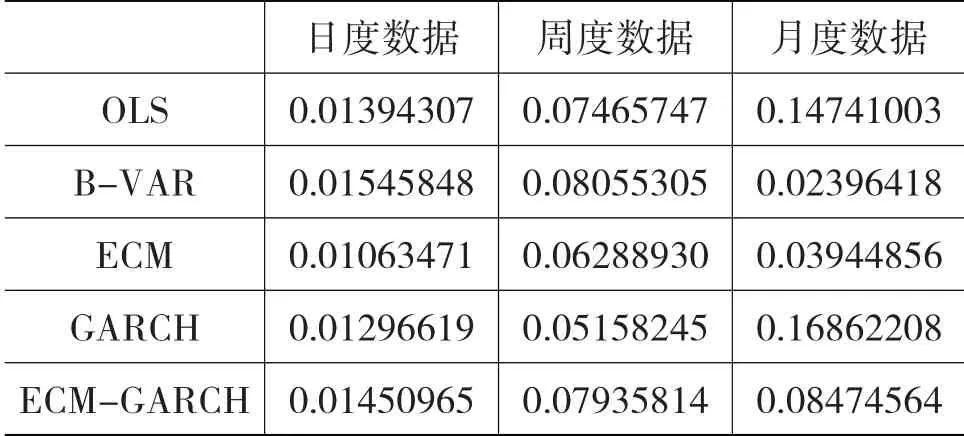
表5 样本区间外的套期保值绩效h值

表4 显示的是期货合约到期前相对较长的时间段所对应的套期保值绩效，计算过程中的套期保值比率值h和变量的方差、协方差是利用2015年1月5日至2018 年12 月28 日这个样本内数据计算而得。表5 显示的是期货合约到期前相对较短的时间段，即临近交割前一段时间所对应的套期保值绩效，计算过程中所使用的套期保值比率值h与表4相同，但变量的方差和协方差是利用2019年1月2日至2020年2月28日这个样本区间外数据计算所得。

表4 显示，套期保值的确降低了保险公司的收益风险。在同一个模型下，随着操作时间间隔从日度到周度，再到月度的逐步增大，套期保值绩效也同步增大。无论是日度、周度还是月度时间间隔，套期保值绩效最高的均为OLS模型或ECM模型。

表5 同样验证了套期保值的确降低了保险公司的收益风险。与表4 相比，在相同的模型和样本时间间隔下，样本区间内数据计算所得的套期保值绩效要比样本区间外数据计算所得的套期保值绩效低，这种现象与理论不一致。因为，从理论上讲，在有效市场上随着到期日的临近期货价格会趋近于现货价格，套期保值应该更为有效，h 值应该更高。反常现象的背后原因可能是目前我国衍生品市场的投机因素还比较多，市场有效性还不够高，削弱了“保险+期货”的部分功能。

四、研究结论及相关建议

本部分将对前文套期保值绩效评估结果进行综合分析，确定最优的套期保值比率，分析“保险+期货”模式在降低保险公司风险方面的效果。最后从保险行业、期货行业、监管机构以及国家政策等四个层面给出建议，为推动“保险+期货”模式良性发展提供参考依据。

（一）研究结论

本文有如下四点主要结论。

第一，保险公司只要参加套期保值，无论选用本文中哪种模型确定套期保值比率，都可以在一定程度上降低风险。这表明“保险+期货”模式下套期保值的确可以分散和转移保险公司面临的价格波动风险，切实提高保险公司抗风险的能力。

第二，样本区间内数据下，OLS模型确定的套期保值比率均为最优；样本区间外数据下，B-VAR 模型确定的套期保值比率基本是最优的。这与其他学者相关的研究结论是一致的：利用农产品期货进行套期保值时，使用OLS 等静态套期保值方法所产生的风险降低程度往往最大。因此，在保险公司利用“保险+期货”模式进行套期保值时，可以优先考虑使用快捷的静态套期保值方法。

第三，其他变量相同时，随着“保险+期货”套期保值的时间周期从日度到周度直至月度的增长，套期保值的效果也会随之逐渐增加。这一特点对于保险公司而言非常利好，因为农业保险所需要对应的“保险+期货”的套期保值期限一般都远长于经销商、加工商等套期保值者，可以使得“保险+期货”模式降低保险公司风险的效果更为显著。

第四，样本区间内数据代表的是距离期货合约到期交割时间较远的数据，样本区间外数据则代表临近交割的数据，研究结果显示样本区间内数据的套期保值绩效均高于样本区间外数据，这一现象与有效市场下的理论结果不符。理论上讲，如果市场是有效的，临近交割时期货价格和现货价格逐渐趋同，基差风险应该逐渐降低，套期保值效果随之提高，后者样本计算的h 值应当大于前者。理论和实践的差异从一个侧面反映了我国农产品期货市场有效性不足的问题，原因可能包括过度投机导致价格的异常剧烈震荡。因此，保险公司在参与“保险+期货”时须保持谨慎态度，及时关注市场行情，动态监督合作伙伴交易行为等。

（二）相关建议

“保险+期货”模式是基于我国当前农业发展和金融发展需要而催生的一项创新产品，其积极作用毋庸置疑。但是在试点阶段难免会出现一些问题，有些问题已经出现端倪，如李铭和张艳（2019）[19]就指出“保险+期货”模式仍存在实际赔付率较低、交易成本较高等问题，并建议可以学习美国农业保险与期货行业合作的成功经验，更好地服务于我国经济发展。有些问题虽未显现，但存在潜在的风险隐患，如套期保值效率有待提高等。我们希望通过相关主体的紧密配合，不断优化“保险+期货”的运行模式，力促农业发展和金融市场完善。本文试图从以下角度提出一些政策建议以供参考。

首先，对于保险行业来说任重而道远，可以从如下三个方面予以改进完善。

一是提高参与意识，注重人才储备。不少保险公司员工对“保险+期货”模式了解程度不够，套期保值、风险防控的理论水平有待提高，阻碍了保险公司的参与积极性。这种现状不利于“保险+期货”模式的全面推进，也不利于保险公司的业务创新。建议保险公司通过增加培训普及“保险+期货”模式知识，培育和引进相关人才，组建专门负责团队等，多方推动“保险+期货”项目，力争早日实现盈利。

二是发挥自身优势，促进市场繁荣。保险公司可以发挥其地缘优势和信息优势，配合政府和商品期货交易所做好“保险+期货”模式的宣传工作，吸引更多农户参与到“保险+期货”市场。例如从整个农产品价格行业上下游进行纵向覆盖，吸引农产品加工商、养殖户、经销商等客户，既能增大保险业务量，增强经营稳定性，也能提高金融衍生品市场的交易量和流动性，促进各金融市场共同繁荣发展。

三是创新保险产品，做好风险防控。一方面，保险公司应当保持对新技术、新概念较高的敏感度，不断创新产品，服务时代发展要求。借力国家对“保险+期货”模式的扶持政策，做好“保险+期货”模式的支持和对接工作，进一步发展完善价格保险和收入保险等农业保险产品。另一方面，保险公司需要加强与期货公司的联动，保持沟通联系，加强关注监督，设立专门准备金应对可能出现的潜在风险。在我国金融衍生品市场的价格波动风险仍然较高的情况下，要为防范系统性金融风险、期货公司的操作风险等做好预先准备。

其次，对于期货等金融衍生品行业而言，主要有如下三个方面的建议。

一是重视员工培训，树牢服务意识。“保险+期货”模式在我国推行时间相对较短，在大众视野中相对陌生，甚至从业人员也未必完全熟悉。作为“保险+期货”的主体之一，期货等金融行业同样需要重视员工培训，促使大家不断丰富专业知识，树牢服务意识，总结实践经验，共同推进“保险+期货”模式的发展。

二是配合产品推广，提高服务水平。配合保险公司和政府，做好“保险+期货”产品的推广工作。指导下属投资子公司或资产管理子公司加强人才储备，增强自身在金融衍生品市场的投资交易水平、风险控制水平以及审核监督水平，帮助保险公司合法合规地分散农业保险的既存风险。

三是丰富衍生产品，完善金融市场。为了日后更完善地服务于“保险+期货”模式，各交易所需要根据市场交易需求和农业保障需求创新期货和期权品种，进一步提升我国金融衍生品市场发展水平，为日后进一步的金融创新开放夯实基础，做好准备。

再次，对于政府和监管机构，本文也有如下三点建议供参考。

一是动态调整政策规定，完善监管制度。为了控制保险公司风险，相关规定对于保险公司直接参与金融衍生品二级市场的交易限制较为严格。在特定历史阶段，这些规定的确保障了保险公司和投保人缴纳保费的资金安全，但是随着经济的快速发展，一些规定可能会渐渐成为束缚业务创新的“阻力”。尽管保险公司采取“保险+期货”模式已经进行了一定的创新，原有政策也进行了一定的调整，但是还有一些制度需要及时进行补充完善，建议相关监管制度及时进行动态调整，以推动我国金融市场不断成熟完善。

二是把握补贴标准，激发市场活力。众所周知，政府补贴会起到释放政策信号、刺激金融市场的作用。如果补贴力度过大，就会弱化市场自主调节的功能；如果补贴力度过小，则起不到激发农户投保和保险公司承保的作用。因此，政府需要把握好补贴尺度，用好政策工具。

三是客观评价成效，促进持续发展。当前某些试点地区习惯性简单地以保险赔付金额作为衡量“保险+期货”模式成效的指标，以此彰显“保险+期货”模式的优势。赔付较少的保险公司，有可能在以后的“保险+期货”招投标过程中处于劣势地位，这种现象可能会增加保险公司的风险隐患，挫伤它们的参与积极性。因此应当逐渐完善评价机制和方法，客观评价保险公司服务地方经济的成效，支持和鼓励保险机构不断创新产品和服务。