黑龙江某地热响应试验数值计算模型研究及应用

高阳，张延军，2，潘逸轩 ，袁学兵

1.吉林大学 建设工程学院，长春 130026；2.吉林大学 地下水资源与环境教育部重点实验室，长春 130026

0 引言

地源热泵技术是利用地表浅层地热能资源作为冷热源进行供暖、制冷的环保技术，因其运行效率高，温室气体排放少，近年来逐步作为传统供热制冷技术的替代[1]。而在地源热泵系统设计过程中，获取准确的岩土体导热系数，钻孔内岩土体温度分布对设计至关重要,影响地源热泵建设成本。确定土壤导热系数的方法有几种，如类型识别、稳态试验、探针试验和热响应试验[2]，其中热响应试验被认为是确定土壤导热系数的最有效方法[3]。

岩土热响应试验最早由Morgensen[4]提出，它将测试设备与埋入地下的U型管相连接形成回路，使经过不断加热的流体在回路中循环，并将热量输入到周围土壤中，实时测量入口和出口水温以及流速。根据实测结果，对数据进行一定处理得到岩土体导热系数。该试验最早用于欧洲地区及美国，瑞典和美国的俄克拉荷马州做了较多实践与研究[5]，国外对于热响应试验数值模型研究一直在进行，Marcotte et al.[6]利用三维数值模型计算的流体平均温度与其提出的p-linear平均值比较，避免了钻孔热阻估计中的偏差；Raymond et al.[7]利用三维数值模型进行了对比TRT模拟，再现了分层地下的传导传热和沿GHE管道的垂直热对流；Simon et al.[8]开发出既能表示短时间尺度又能表示长时间尺度的传导和流体循环过程的钻孔热交换器模型，研究强调了模拟热传递随深度变化的重要性，以及在短时间尺度内模拟管道和灌浆之间动态相互作用的重要性；Franco et al.[9]等利用数值模拟来展现具有不同材料特性、尺寸和管道配置的合成能量桩系统的热响应测试结果；Gashti et al.[10]基于COMSOL MultiphysicsTM构建了三维数值模型模拟了钢桩基地埋管换热器的加热/冷却过程。

中国热响应试验的研究与应用较晚，主要出现在2000年后[11],邓军涛等[12]对岩土初始平均温度和综合导热系数的不同获取方法进行对比分析，结果表明无功循环平均温度及现场热响应试验得出导热系数值作为系统设计参数更为接近实际工况；官燕玲等[13]建立了岩土热响应试验的三维数值计算模型，研究了岩土热响应试验放热与取热方法对结果的影响、试验结束后土壤温度场的恢复以及试验初始时刻值的舍去对分析结果的影响；李新华等[14]利用数值模拟技术研究了热扩散变化规律；王沣浩等[15]建立了三维数值模型，采用不同的参数识别方法计算了土壤的导热系数，还分析了测试时间、可变数据质量、钻孔半径、初始地温和热注入速率的影响; Li et al.[16]建立二维模型研究了地埋管两支管间的传热特性，给出了短路热阻的最佳拟合表达式，并建立一个三维等效矩形数值模型来评价流体沿管道的温度变化，分析了流速和浆液电导率以及钻孔深度对外部温度、钻孔流量和单位长度短路损失率的影响;李锦堂等[17]建立了岩土热响应试验动态仿真模型，研究了试验持续时间的影响、加热功率、加热功率波动、管内流速和数据记录间隔的影响。

笔者基于COMSOL MultiphysicsTM软件，在前人研究基础上，建立三维岩土热响应试验数值计算模型，并利用实测的热响应试验数据进行验证，探究回填材料性质、加热功率对热响应试验结果的影响以及地埋管周围温度场的变化，为原位岩土热响应试验提供参考。

1 场地条件

热响应试验场地位于黑龙江北部，测试时间为11月上旬，试验符合DZ/T0225—2009《浅层地热能勘察评价规范》和GB50366—2005《地源热泵系统工程技术规范》，方法是通过地埋管对钻孔施加恒定的热流，测量加热功率、地埋管内换热流体的进出口温度、流量等参数。

1.1 原位岩土层结构

原位岩土层结构图如图1所示。

1.2 试验条件及参数

本次试验地埋管选用直径26 mm的U型HDPE管，钻孔直径16 cm，埋深100 m，钻孔回填材料为细砂+膨润土，设备加热功率设定为4 200 W。其余参数见表1。

表1 热响应试验参数

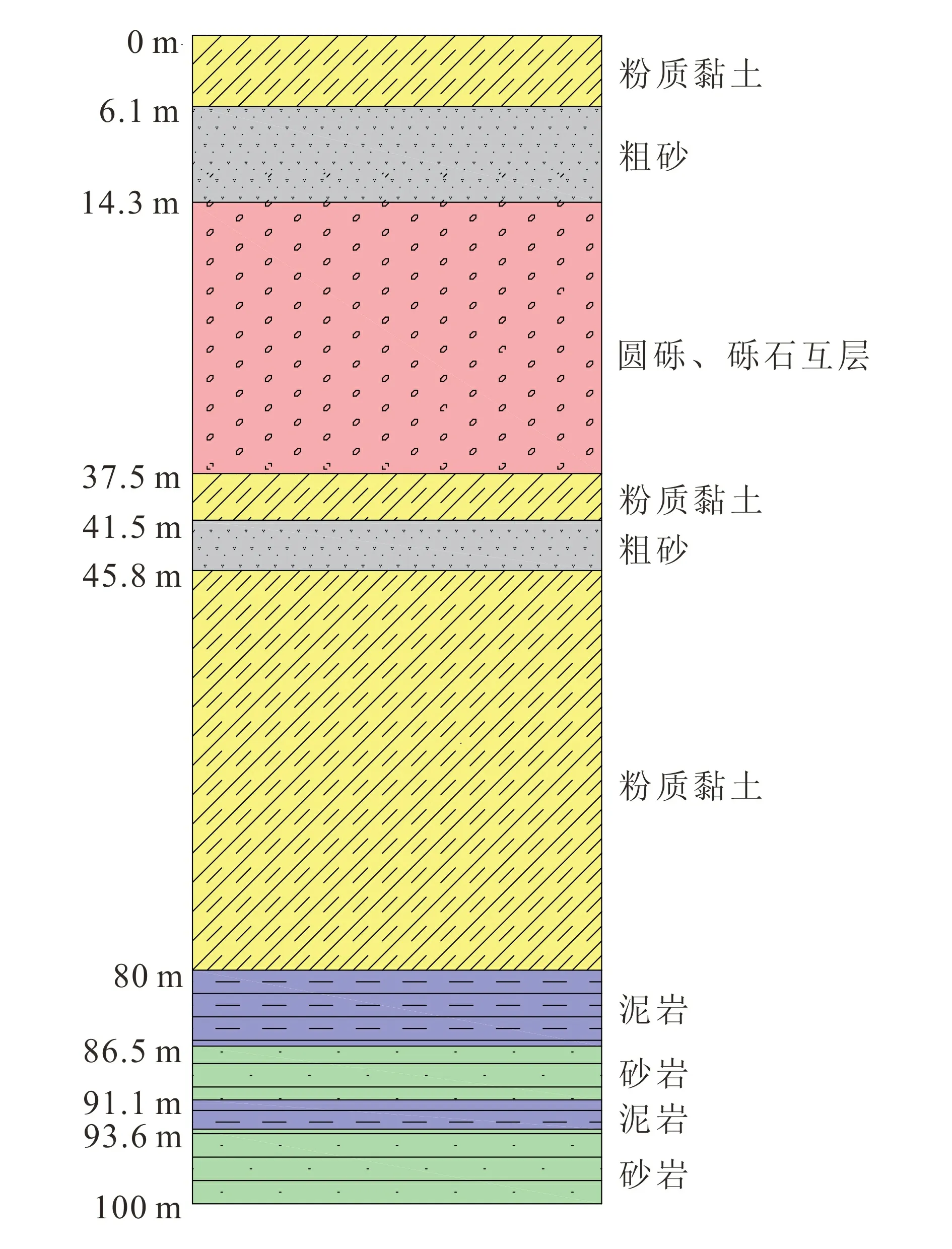
图1 原位岩土层结构Fig.1 In situ structure of rock and soil

1.3 岩土热物性参数

根据《地源热泵系统工程技术规范》GB50366—2009[18]中附录C的公式，岩土热物性参数包括岩土综合导热系数、岩土比热容可根据式(1)、(2)进行计算。

(1)

(2)

其中式(1)可改写为：

Tf(t)=k·ln(t)+m

(3)

(4)

式中：Tf为τ时刻循环介质平均温度，℃；Tff为无穷远处土壤温度，℃；ql为每延米换热量，W/m；Rb为钻孔内传热热阻，K/W；db为钻孔直径，m；do为埋管外径，m；di为埋管内径，m；D为埋管中心距，m；λp为埋管导热系数，W/(m·K)；λb为回填材料导热系数，W/(m·K)；h为循环介质与管壁对流换热系数，W/(m2·K)。

Tf(t)可以由(埋管进口温度+埋管出口温度)/2得到，进出口温度曲线如图2所示。通过式(3)对Tf(t)曲线进行拟合得到岩土综合导热系数为2.93 W/(m·K),然后计算岩土比热容cs为545.5 J /(kg·K)。

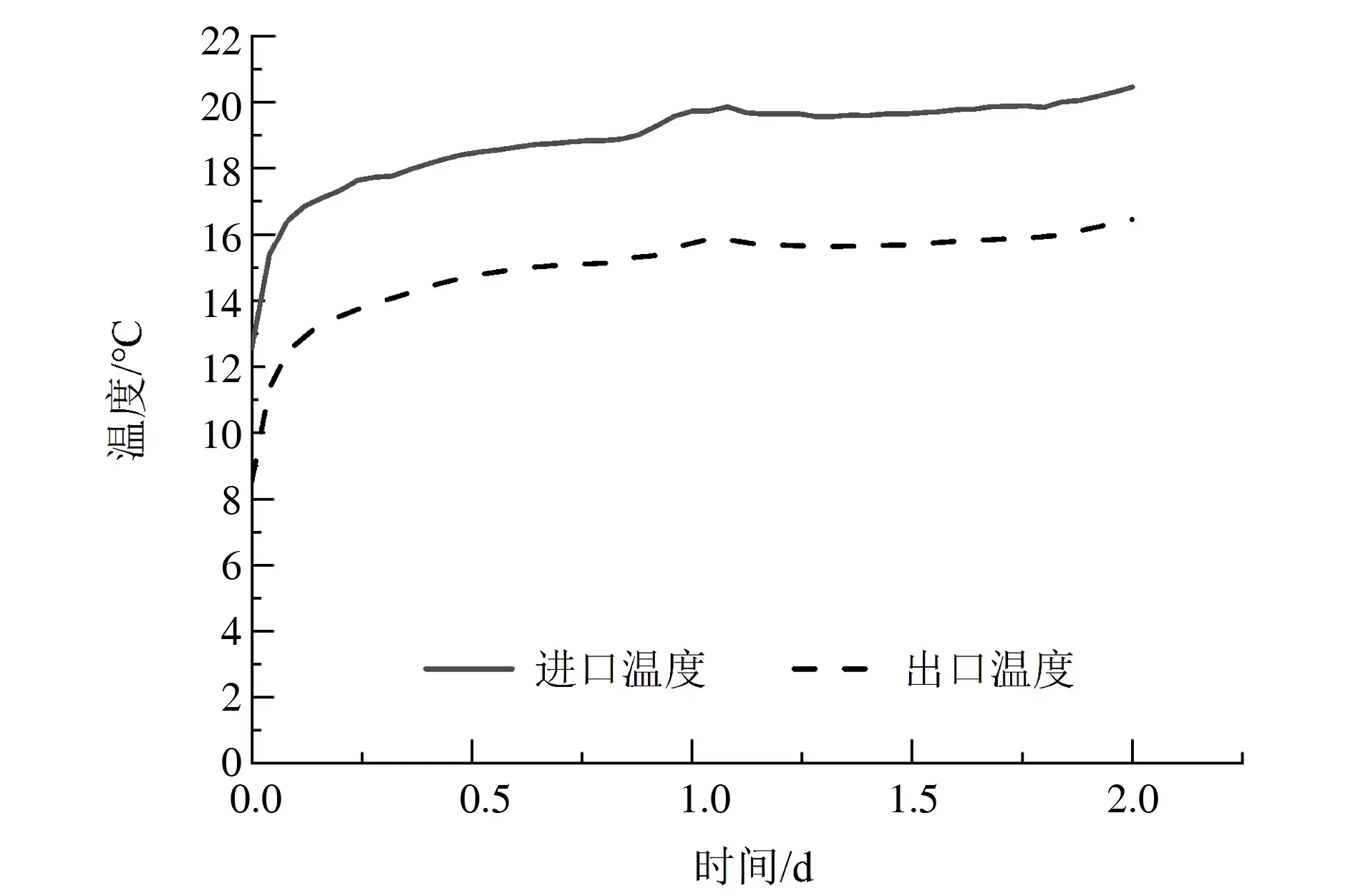
图2 埋管进出口温度Fig.2 Inlet and outlet temperatures of bured pipes

2 数值模拟

2.1 初始条件与边界条件

根据现场岩土体温度测量，初始平均温度为6.5℃，设模型表面温度(z=0)为大气环境温度，值为-5.8℃，其余边界均为热绝缘边界。设地埋管进口温度为Tin,出口温度为Tout,二者之间的关系[19]:

(5)

式中：power为加热功率,W；ρ为循环介质密度,kg/m3；Cp为循环介质比热容,J/(kg·K)；v为循环介质流速,m3/s，其中循环介质流速恒定为2.7e-4 m3/s。

2.2 岩土-地埋管耦合传热模型

如图3所示，构建了尺寸为(5×5×100)m的三维数值模型，其中钻孔深度100 m，半径0.08 m，U型管弯曲部分被简化为直角，模型基于COMSOL MultiphysicsTM中非等温管道流以及多孔介质传热模块，其中非等温管道流将U型管简化为一维线性单元，通过非等温管道流模块中壁传热的选项，将管道流与周围土壤耦合起来。

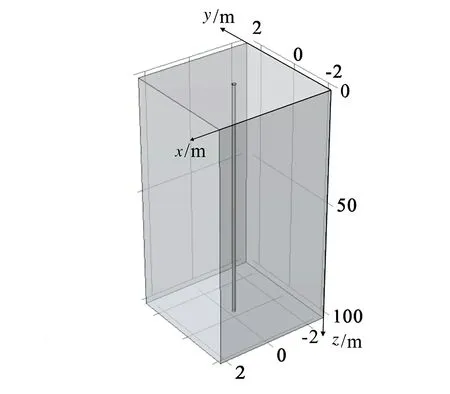
图3 几何模型Fig.3 Geometric modeling

2.3 控制方程

对于不可压缩流体，管内流体与管壁之间的热平衡方程为[20]：

(6)

式中：Cp为循环介质比热容,J/(kg·K)；u为流体切向速度,m/s；k为导热系数；fD为黏性系数；dh为平均水力直径,m；Q为广义热源,W/m；Qwall为流体与管壁热交换,W/m，其中Qwall可用以下公式计算：

Qwall=(hZ)eff(Text-T)

(7)

Text为管壁外侧温度；(hZ)eff为对流换热系数与管壁周长乘积的有效值,W/m·K。

2.4 模型验证

为确保模型可靠性需要对其进行验证，在岩土热响应试验中，最直观反映结果的数据为进出口温度，因此将试验的进出口温度与模拟结果进行对比。如图4所示，经计算，模拟值与试验数据之间绝对误差平均值为 0.18℃，因此可以认为模拟结果基本可靠。

图4 数值模拟进出口温度与试验结果对比Fig.4 Comparison of inlet and outlet temperatures between numerical modeling and thermal response test results

3 模拟结果与相关问题讨论

3.1 地埋管换热对岩土体温度场影响

在热响应实验进行过程中，地埋管周围的岩土体温度也会不断变化，分别给出试验进行0.5 d、1 d、1.5 d、2 d时钻孔周围截面温度云图(图5)。

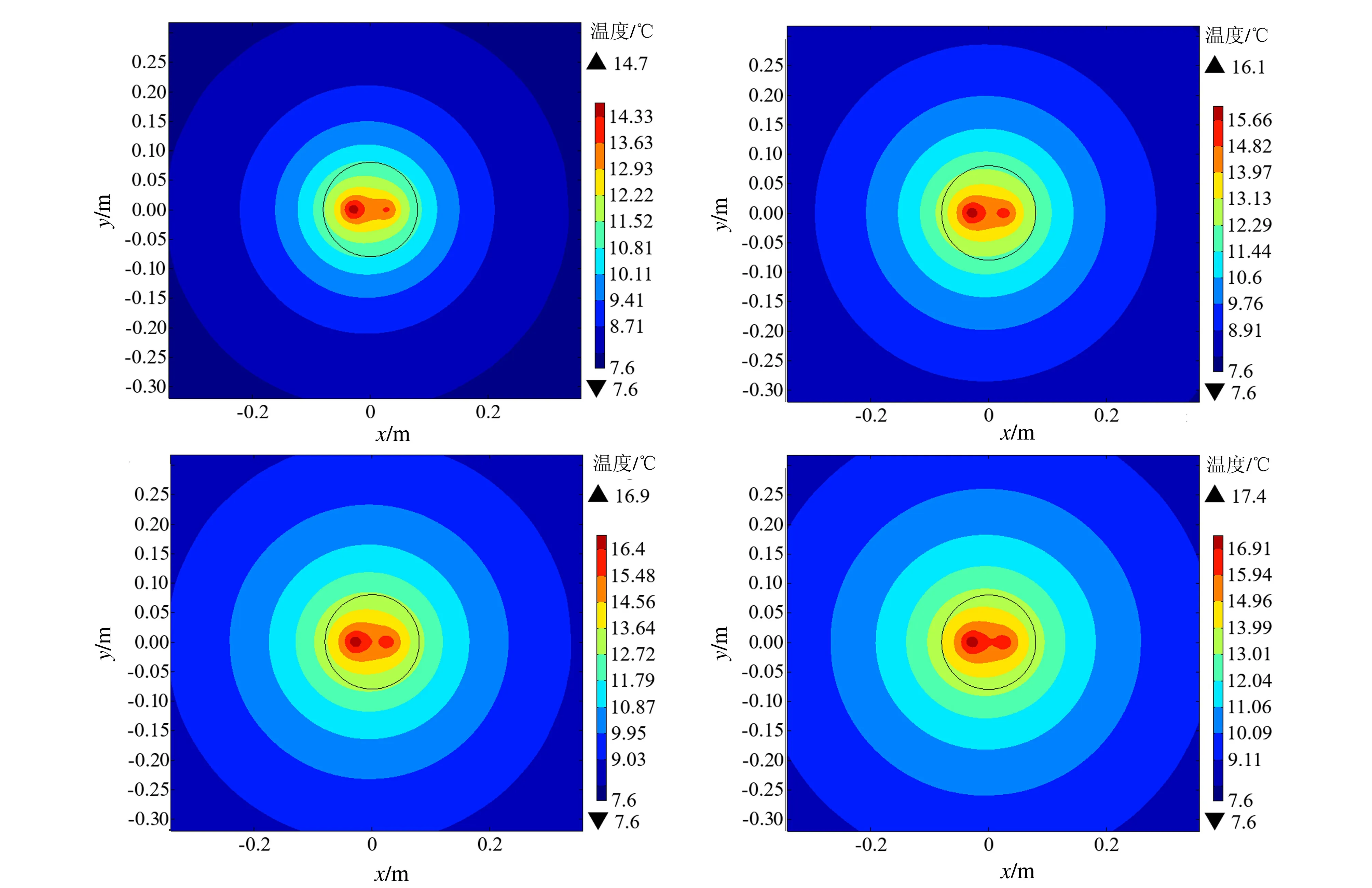
图5 钻孔周围温度变化云图 Fig.5 Cloud maps of temperature changes around borehole

在试验时间持续2 d时间内岩土体温度场最大的影响范围约为2.4 m。根据模拟结果，在距离钻孔中心2.4 m外的点温度变化曲线基本趋于平缓，变化值<0.01℃(图6)。

图6 距钻孔不同距离的温度变化曲线Fig.6 Temperature change curves at different distances from borehole

同时也给出了从试验开始到结束，再到结束后地温恢复阶段的温度变化曲线，图7中显示出该点在试验结束后8 d内温度基本恢复，尤其在2 d内最快，但始终无法恢复到岩土体初始温度，若要进行下次试验，最好在结束后8 d后进行。

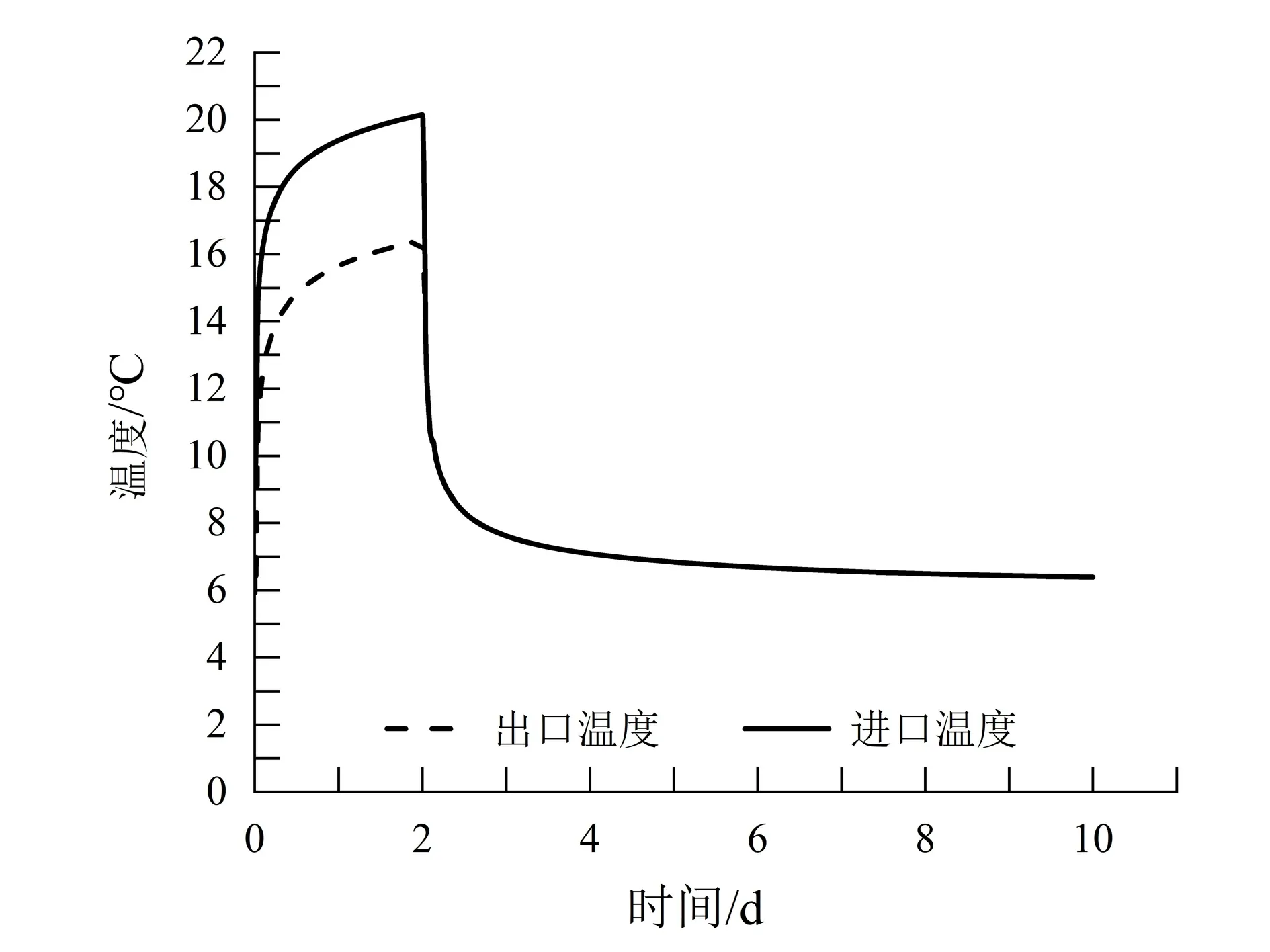
图7 温度恢复曲线Fig.7 Temperature recovery curves

3.2 回填材料性质对岩土体导热系数的影响

为探究钻孔回填材料性质对岩土体导热系数的影响，在其他要素不变的条件下，改变回填材料的恒压热容，分别取1 880、1 580、1 280、980、680 J/(kg·K)，得到地埋管换热器平均温度的变化曲线，同理，控制其他要素不变，改变钻孔回填材料的导热系数，分别取2.3、2.1、1.9、1.7、1.5 W/(m·K)，需要注意的是钻孔回填材料导热系数改变会引起变化进而导致岩土比热容发生变化，表2给出了不同导热系数下的岩土比热容的值，总体影响较小。最后根据公式(3)、(4)进行拟合，得到不同条件下岩土体综合导热系数，观察其变化，总结回填材料性质对岩土体导热系数的影响。由于在试验初期换热工况未达到稳态，故删除前0.6 d数据进行拟合。

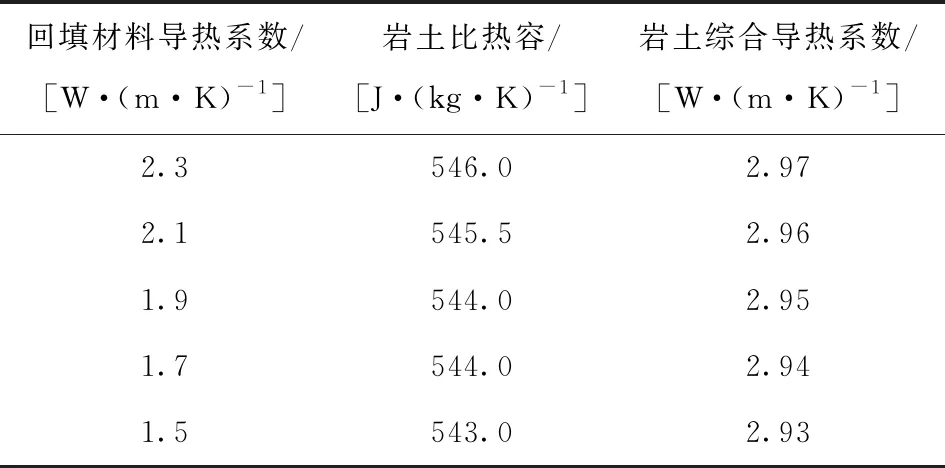
表2 回填材料导热系数的影响

表3 回填材料比热容的影响

计算结果已在表3、4中列出，由结果分析可得：回填材料每增加0.2 W/(m·K)，岩土综合导热系数平均增加0.01 W/(m·K);回填材料恒压热容每增加300 J/(kg·K)，岩土综合导热系数平均减少0.105 W/(m·K)，总体来说回填材料性质对热响应试验有一定影响。

3.3 加热功率对热响应试验的影响

如图8所示，加热功率的变化会引起地埋管内循环流体平均温度发生变化，但是对岩土综合导热系数的影响还需要进行分析，因此控制其他因素不变，加热功率设置为4 200 W、4 900 W、5 600 W、6 300 W和7 000 W，根据线热源模型公式分别计算其岩土综合导热系数。

图8 不同加热功率下的循环流体平均温度Fig.8 Average temperature of circulating fluid under different heating power

根据表4进行分析，可以看出加热功率对岩土综合导热系数几乎没有影响。

表4 加热功率的影响

4 模型应用

为探究地埋管换热在冬季工况下对岩土体温度变化以及换热量的影响，本文利用已经过验证的模型对冬季工况进行模拟。

黑龙江地区冬季供热期达6个月，约180 d，取地埋管进水口温度1℃，每天运行12 h，循环流体流量为0.97 m3/h，模型几何尺寸为(6×6×100)m。

根据模拟结果如图9所示，在设备运行期间，其最低温度随时间不断降低，但降低的温度在不断减少，趋于平缓；设备停运期间温度在恢复，然而每日停运期最大温度也在不断降低，变化趋于平缓。经分析产生该结果的主要原因是随着地埋管换热，钻孔及其周围岩土体温度不断降低，且影响范围不断增大，相同进水温度下换热量不断减少，同时从外部岩土体得到的温度恢复量及速度也在变小。

图9 前30 d出口温度变化Fig.9 Outlet temperature changes in the first 30 days

最终在运行180 d后，出口温度为2.21℃，在整个运行期间，埋管进出口平均温度为1.66℃，经计算U型管每延米换热量为33.7 W/m。

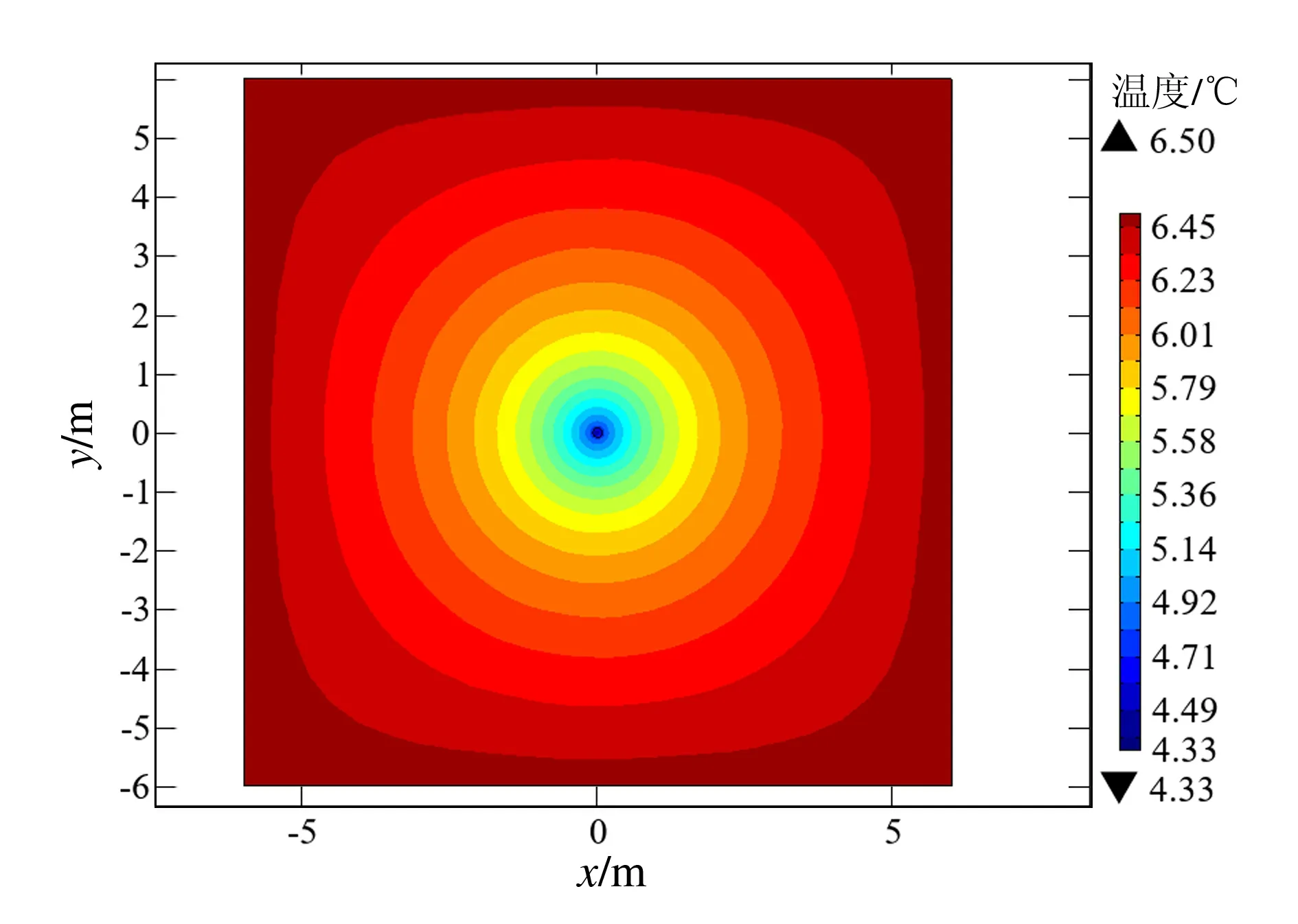
图10 供暖期180 d后的温度云图Fig.10 Temperature cloud diagram after 180 days of heating period

图10为温度影响范围，180 d后温度影响范围达到5.7 m，因此地埋管间距应>6 m。温度影响范围内岩土体平均温度为6.18℃，降低了0.32℃；钻孔内最低温度为4.33℃，平均温度为4.42℃，降低了2.08℃。

5 结论

(1)通过COMSOL中的非等温管道流模块与多孔介质传热模块结合现场试验数据建立三维岩土热响应试验数值模型，经验证，该三维模型及数值方法可以实现对现场热响应试验的模拟。

(2)岩土热响应试验持续2 d时间内，其温度场影响范围可以达到2.4 m，且在试验结束后，温度在2 d内恢复最快，8 d内基本恢复。

(3)回填材料导热系数每增加0.2 W/(m·K)，岩土综合导热系数平均增加0.01 W/(m·K); 回填材料恒压热容每增加300 J/(kg·K)，岩土综合导热系数平均减少0.105 W/(m·K)。同时，加热功率对岩土综合导热系数几乎没有影响。

(4)在冬季运行工况下，设备每日运行期间最低温度及非运行期最高温度不断降低，运行180 d后，出口温度为2.21℃，在整个运行期间，埋管进出口平均温度为1.66℃，经计算U型管每延米换热量为33.7 W/m；180 d后温度影响范围达到5.7 m，因此地埋管间距应>6 m。温度影响范围内岩土体平均温度为6.18℃，降低了0.32℃；钻孔内最低温度为4.33℃，平均温度为4.42℃，降低了2.08℃。