低温工质润滑螺旋槽止推轴承中空化现象研究

颜少航，赖天伟，刘玉涛，杨申音，丁文静，侯 予

（1.西安交通大学能源与动力工程学院，西安 710049；2.北京航天试验技术研究所，北京 100074；3.北京卫星环境工程研究所，北京 100029）

0 引言

高速离心泵在低温工质的输送领域已有广泛的应用[1]，工质自润滑轴承凭借无污染、可靠性高、体积和质量较小的优点，在液氢、液氧高速离心泵中广泛应用[2]。由于螺旋槽止推轴承在稳定性和承载力方面具有优势，使其成为最为常用的自润滑轴承之一。然而低温工质润滑轴承中的空化现象会对轴承的运行性能产生极大地影响。

空化是液体工质在局部压力降低的情况下，由压力驱动而发生的内部产生蒸气气泡或空穴的过程[3]。空化的形成和溃灭过程将导致液体自润滑轴承工作面出现凹坑和剥蚀[4]。当轴承发生空化时，会出现噪音、振动和效率降低等问题[5]，影响机械系统运行的可靠性。因此，基于Rayleigh-Plesset方程建立了许多空化模型来模拟和预测水力机械中的空化现象。空化气泡的生长过程与流体黏性、表面张力和相界面的热质传递过程密切相关[6]。现有的常用空化模型在推导过程中没有考虑热力学效应的影响，虽然能较好地模拟常温非热敏感型工质（如水等）的空化现象，但很难模拟液氮、液氢等低温工质空化过程。为了衡量流体工质的热敏感程度，引入热力学标准温度降[7]，水在空化过程中的热力学标准温度降远小于液氮和液氢，同时其液/气密度比远高于液氢和液氮。由此可知，对于低温流体，当形成与水相同尺寸的气泡时，需要更多的液体工质气化，这一过程将吸收大量的气化潜热，导致气泡内温度下降。因此热敏感型低温工质的空化过程对热效应更为敏感，需要考虑热效应对空化模型进行修正。

常用的空化模型在推导过程中假设空化发生在无限大空间，忽略表面张力。液体自润滑轴承具有高转速、高剪切等特点，几何特征明显与空化模型推导时所采用的假设不符。Canedo等[8]在1993年使用两个高速相对转动的同心圆柱进行实验，观察到气泡在高速剪切作用下，受表面张力影响的变形过程，并引入毛细管数Ca。实验表明：当毛细管数Ca＞1时，气泡生长过程中的表面张力不可忽略。

本文采用Rayleigh-Plesset方程，综合考虑表面张力、热力学效应和湍流效应的影响，对现有的ZG-B空化模型进行修正；基于Hord的实验结果[9]，对液氮和液氢绕流二维翼型空化流动进行数值模拟，验证修正空化模型的正确性；最后将修正空化模型应用于液体自润滑止推轴承中，研究修正空化模型作用下和不考虑空化条件下轴承中承载力随转速的变化规律。

1 空化模型修正

本文选取Z-G-B空化模型进行修正。Zwart等[10]提出的Z-G-B空化模型是根据Rayleigh-Plesset方程建立的关于蒸汽相体积分数输运方程。Rayleigh-Plesset方程描述了液相中气泡的生长过程：

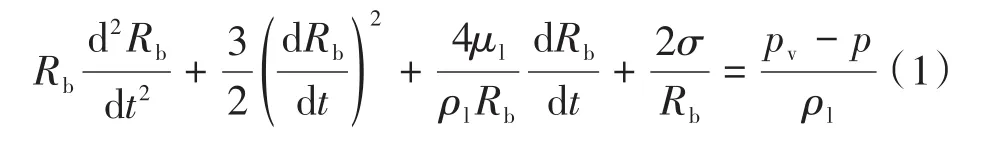
式中：Rb为气泡半径；μl为液相动力黏度；σ为表面张力系数；ρl为液体工质密度；pv为液体工质饱和蒸气压；p为气泡生长的环境压力；t为时间。保留式（1）中的表面张力项并忽略二阶导项和黏度项，可得到气泡半径的生长速率。根据气泡的生长速率可求得气泡体积的增长速率，分别与蒸发、冷凝系数及蒸气密度相乘后可求得气液两相间的质量传输率：

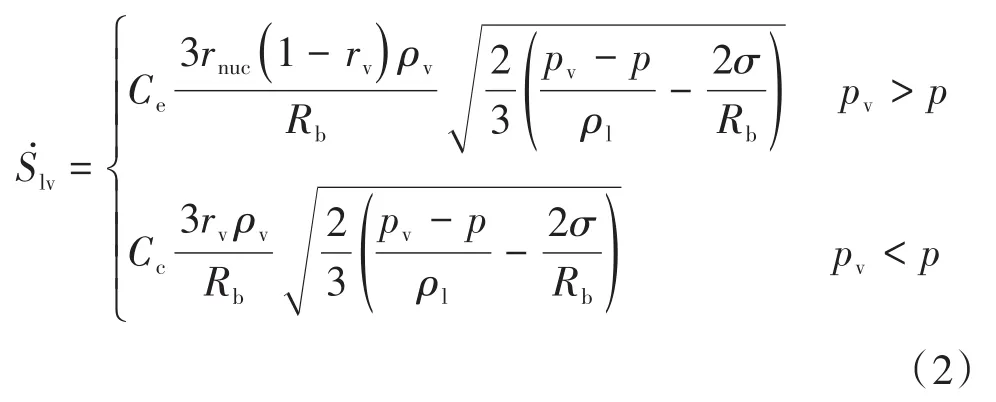
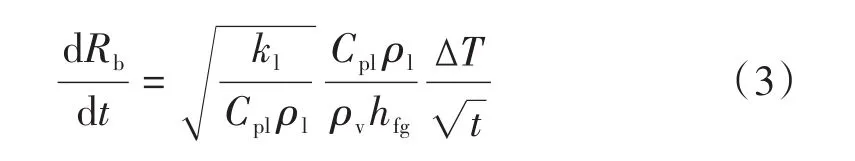
式中：Cpl为液体的定压比热容；kl为液体导热率；hfg为液体的相变潜热；ΔT为液体工质和气泡的温差。此外，空化流动中的湍动能会对空化流动产生重要影响，一般会增大空化效应，无法忽视。根据Merkle等[12]所提出的方法对空化过程中的饱和蒸气压进行修正。综合考虑表面张力、热力学效应和湍动能对空化的影响，可以得到修正空化模型：

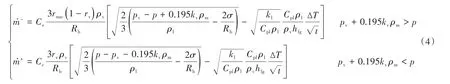
2 空化模型验证

为了对比修正空化模型和Z-G-B空化模型的计算结果，使用Fluent软件编写UDF（User Defined Function）程序对两种模型进行验证。统一采用Realizable k-ε湍流模型，模型参数一致，采取压力入口和压力出口条件，具体压力参数采用参考文献[9]的实验条件。根据参考文献[11]，设置式（4）中蒸发系数Ce=5，冷凝系数Cc=0.001。选取Hord水翼绕流实验中的248C、258C、290C和296B四个工况对模型进行验证。

以液氮为工质的296B工况的模拟结果与实验结果对比如图1所示。从图中可看出，液体工质在翼型头部滞止，此处温度高于入口温度；液体工质进入空化区域，发生空化吸收相变潜热，温度骤降；液体工质离开空化区域后，温度回升并沿翼型表面逐渐减小。压力作为空化的驱动力，其低压区域与空化区域基本一致。修正空化模型计算的温度和压力曲线基本都在实验结果的误差限内，而Z-G-B模型计算的温度曲线和压力曲线与实验所测得的温度和压力差别较大（图1虚线圈中所示）。这表明原有Z-G-B空化模型计算得到的低温和低压区域长度明显大于实验结果，而修正空化模型对空化区域长度的计算结果明显优于Z-G-B模型。

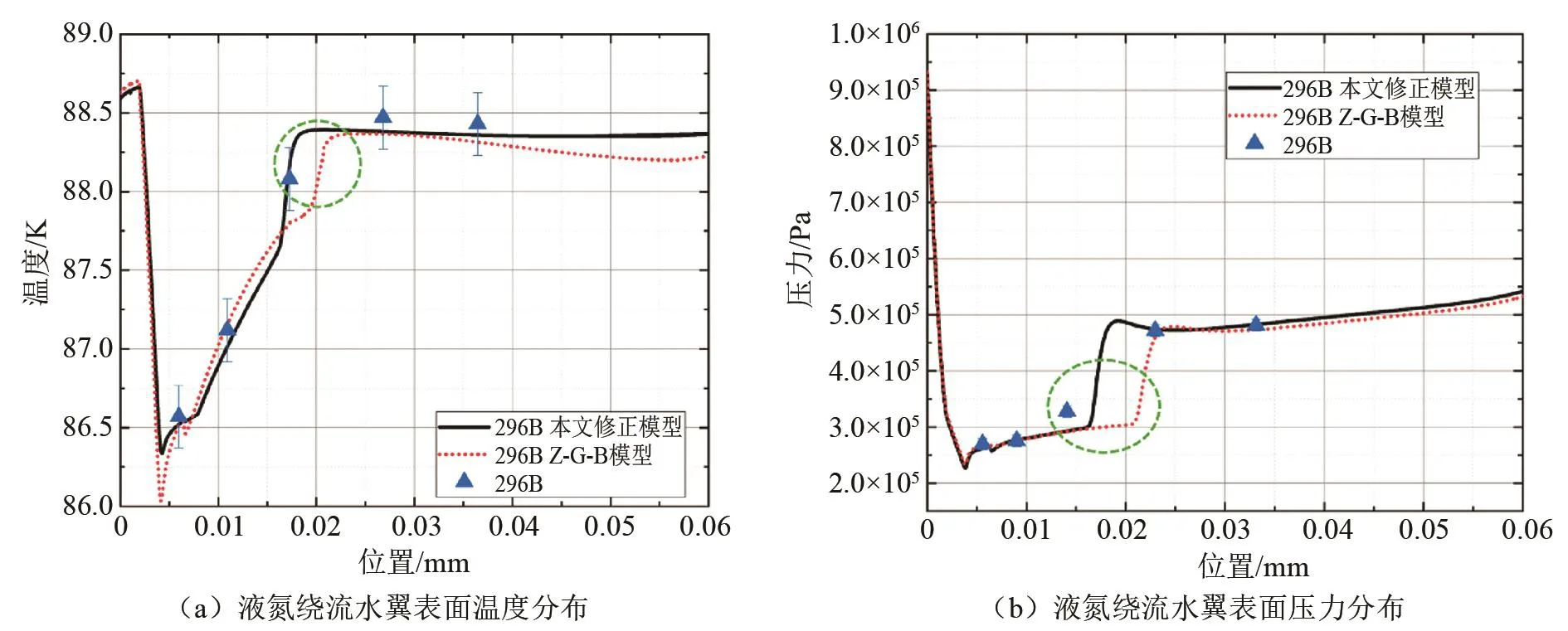
图1 液氮296B工况的温度和压力数值模拟结果与实验结果对比Fig.1 Comparison of temperature and pressure numerical simulation results with experimental results for liquid nitrogen 296B

参考文献[13]的空化模型与修正空化模型的计算对比结果如表1所列，空化区域长度分别由文献[13]模型和修正空化模型计算得到，并与Hord水翼绕流空化实验结果[9]进行对比。从表1可以看出，修正空化模型计算得到液氮的空化区域明显缩短，与实验结果更接近。修正空化模型计算所得的空化区域长度与实验结果之间的偏差比参考文献[13]模型计算的偏差低一半，表明修正空化模型更适用于液氮和液氢低温工质的空化模拟。

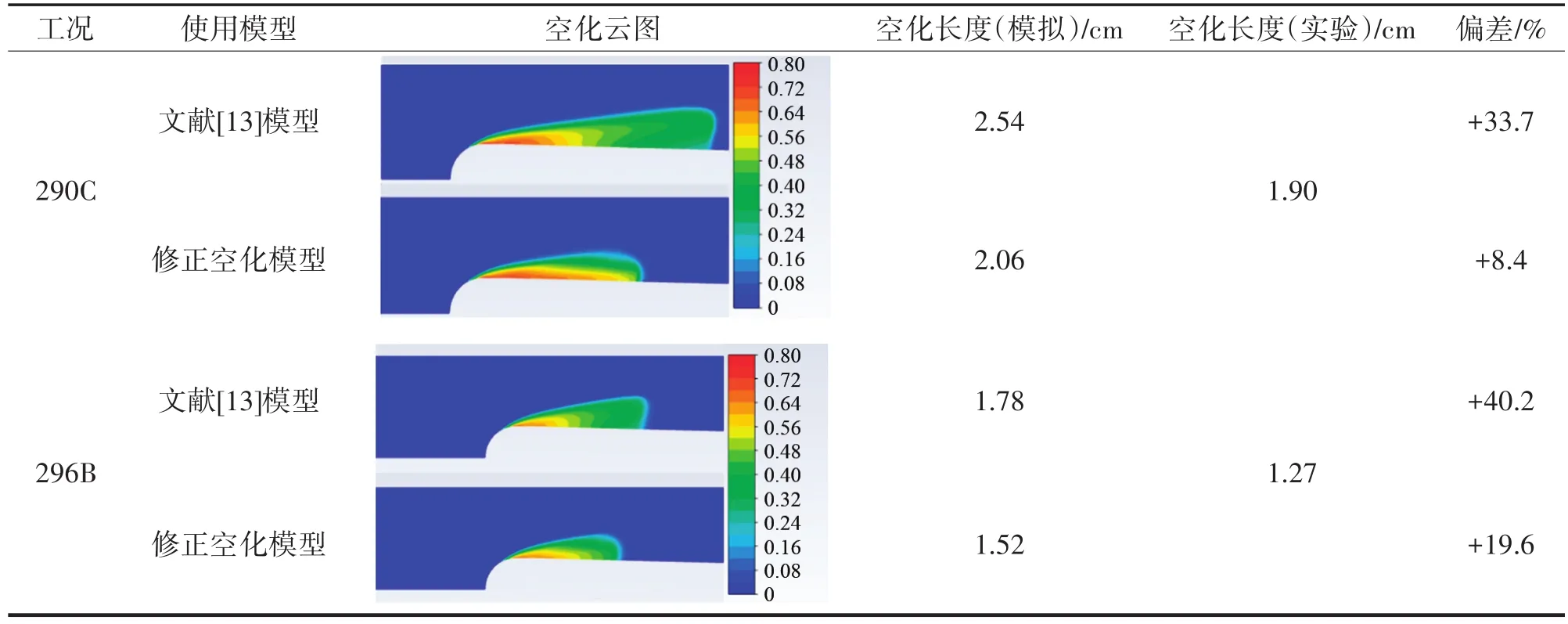
表1 不同空化模型计算空化长度与实验空化长度对比Tab.1 Comparison of cavitation length calculated by different cavitation models and experimental cavitation length

3 修正空化模型在止推轴承中的应用

将修正空化模型应用于液氮润滑的螺旋槽止推轴承中。轴承止推盘设有10条沟槽，槽深与气膜厚度均为10 μm，槽台比为1∶1，止推盘半径为30 mm。使用结构化网格和非结构化网格混合的方法对轴承流域进行网格划分，并进行网格无关性验证，结果如图2所示。网格数160万时计算得到承载力为589 N，网格数192万时计算得到承载力为606 N，两者相差3%左右，可认为此时计算结果与网格数目无关，为了节省计算时间，最终选取160万网格数进行计算。

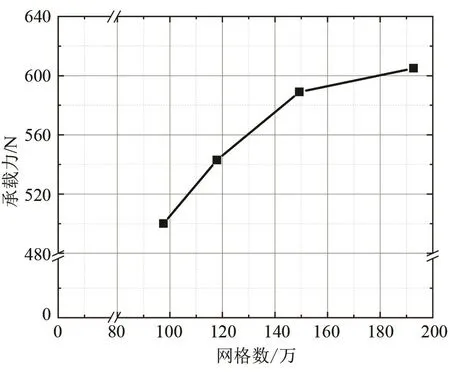
图2 轴承网格无关性验证结果Fig.2 Verification results of bearing mesh independence

轴承的运行温度为80 K，出入口压力均为0.15 MPa。当轴承转速为10 000 r/min时，止推盘压力分布、空化区域分布和温度分布如图3所示。止推轴承的高压区域出现在中心槽角位置，高压区域面积较其他模型的计算结果更大。图3（b）中轴承空化出现的位置与图3（a）中轴承低压区位置基本重合，空化沿着沟槽由止推盘周围向中心发展，而止推盘沟槽前缘的空化较后缘更为严重。由于空化相变过程吸收气化潜热，因此图3（c）所示轴承的低温部分与图3（b）的空化位置基本重合，空化程度越深，温降越大。在非空化区域，使用不同模型计算得到温度分布基本相同。

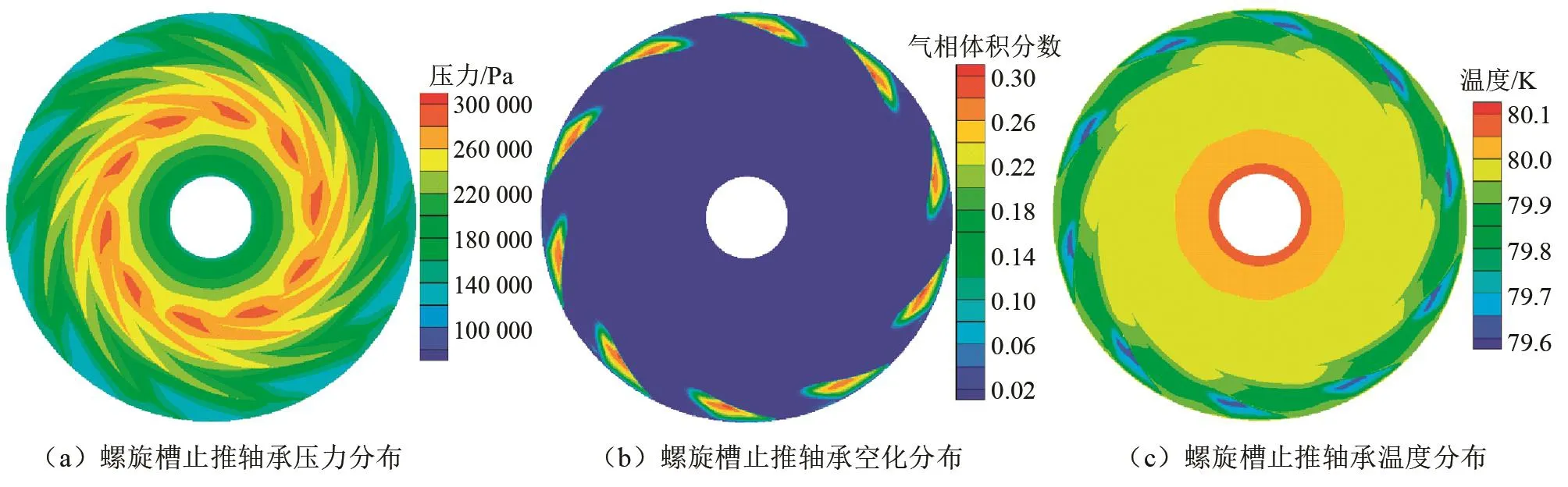
图3 应用表面张力修正空化模型的螺旋槽止推轴承的数值计算结果Fig.3 Numerical results of spiral groove thrust bearing using cavitation model corrected by tension

对轴承承载力和摩擦力矩随转速的变化规律 进行了研究，如图4所示。从图中可看出，由于空化的存在，轴承的承载力明显低于未考虑空化的轴承，并且随着转速的增加和空化程度的加深，两种方法计算的承载力差异逐渐增大。轴承摩擦力矩的变化趋势与承载力类似，空化现象导致轴承的摩擦力矩减小。

图4 螺旋槽止推轴承承载和摩擦力矩随转速变化Fig.4 Spiral groove thrust bearing capacity and friction torque change with speed

4 总结

推导得到修正的空化模型，并以高速离心泵中的低温介质自润滑螺旋槽止推轴承为研究对象，对轴承的承载力和摩擦力矩进行数值研究，并与无空化条件下的轴承运行性能进行对比，得到以下结论：

（1）根据轴承高剪切力和受限空间的特点，基于Rayleigh-Plesset方程，综合考虑表面张力和热力学效应对空化的影响，对Z-G-B空化模型进行了修正得到修正空化模型；

（2）修正空化模型数值计算结果与Hord实验结果的温度、压力场基本一致，此外，本文空化修正模型和原有模型相比，模拟计算所得到的空化区域长度、温度和压力分布与实验结果更接近；

（3）修正空化模型应用于螺旋槽止推轴承的模拟中，结果显示：由于空化的存在，螺旋槽止推轴承的承载力与摩擦转矩均会出现明显下降。