基于反向学习改进人工蜂群算法的分水闸门控流优化

贺弘扬

（杨凌职业技术学院 水利工程分院，杨凌712100）

灌区渠道控制结构通常都是选择平板闸门，但在实际使用过程中平板闸门对控水精度不足，容易产生过量放水或放水量不足的极端情况[1-2]。只有在掌握准确流量的条件下，才能计算出特定时间中的水量数据。当分水闸门处于不同的出流程度下时，需要采用合适的流量方法，前期已有资料论述了闸门控流的模型。目前主要存在平底坎堰流与闸孔出流两种主要的闸门出流形式，其中，闸孔出流包含了自由与淹没出流两种形式[3-4]。

对于闸门处于不同的上下游液位区间内时，实际流量调节范围也存在一个合适的范围，根据上述区间范围设置相应的流量，可以运用终端处理器并结合具体表达式计算获得合适的闸门开度，利用处理器设置编码程序来实现对步进电机的控制，再设置合适的闸门开度，由此实现调节流量的效果[5]。当闸门的上下游处于不同的液位状态下时，将会对流量大小也产生影响，这就要求处理器按照实时参数调节闸门开度，从而与闸门的上下游液位形成良好匹配状态，确保整体流量保持定状态[6]。

当闸孔保持自由出流的控制状态时，可以利用设定闸门开度的方式实现流量的调控功能；在闸孔保持淹没的出流状态下时，虽然可利用调控闸门开度的方式获得所需的流量，而处于淹没出流情况下形成射流或处于不同流速系数下时都会引起计算结果的变化，无法达到对流量的准确调控效果；进入堰流阶段时，不同闸门开度并不会引起闸门流量变化[7-8]。为实现流量的稳定调控功能，应通过控制器对闸门开度进行准确调节，使闸门一直保持闸孔自由出流的状态，防止造成淹没出流或堰流的情况，确保不会对控流准确性造成干扰，最终获得稳定流量[9]。

根据闸孔自由出流计算表达式中的各物理量关系可以发现，闸门开度是影响流量变化的最主要因素。当实际流量相对设定流量之间存在较大差异时，只能根据流量测试与阀门开度调控的反馈方式进行，导致实际调节效率非常低，并且需花费大量处理时间[10-11]。

针对以上分析结果，为提升阀门与流量的调节效率，可以结合实际流量与上下游的液位参数，利用合适的算法计算获得合适的闸门开度，从而将闸门开度快速调控至计算目标位置，接着继续通过负反馈方式进行精确控制，按照以上方式可以实现控制效率的显著提升。本研究选择经过改进处理的人工蜂群算法来计算得到闸门开度最优值。

1 将反向学习运用于人工蜂群算法

不同于其它智能算法，采用ABC 算法进行搜索时的范围包括局部与整体部分，非常适合蜜源的问题分析，有助于更快获取最优解。以ABC 算法进行控制时只需少量几个关键参数便可以实现，能够通过多种类型的编程语言进行处理，并且可以达到理想的收敛状态，因此可以利用ABC 算法来实现各项参数的高效优化[12]。

为人工蜂群算法引入反向学习的过程时，具体方式是在种群初始化期间，已经完成蜜源的初始化情况下，对反向蜜源也实施初始化，此时蜂群依次采集初始与反向蜜源，由此获得最佳适应度蜜源，从而计算得到最优解。

上述研究结果表明，在初始化蜜源过程中加入反向学习方法时，有助于获得更多样化的蜜源，对于计算最优解也具有良好的帮助。以下为反向蜜源计算式：

图1所示为设置反向学习模式时的人工蜂群算法流程。

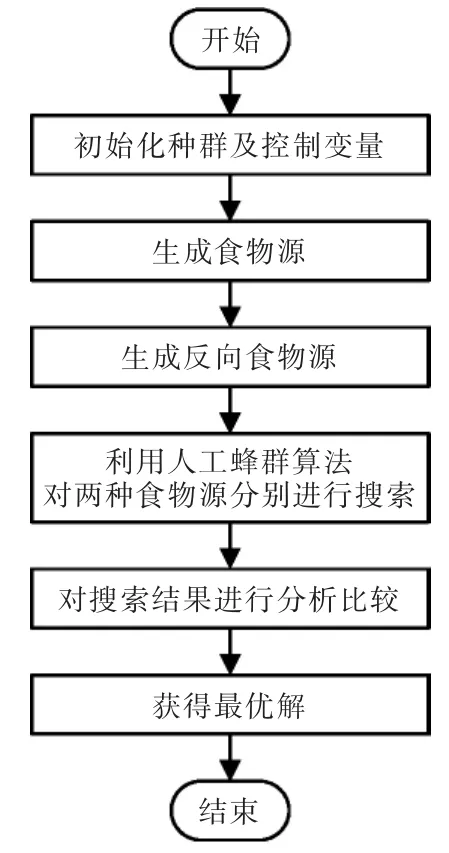
图1 反向学习改进人工蜂群算法流程Fig.1 Flow chart of reverse learning to improve artificial bee colony algorithm

通过人工蜂群算法同时搜索正向蜜源与反向蜜源，之后跟正、反向蜜源最优解实施对比，由此确定最优解。

2 最优闸门开度应用分析

当闸孔保持自由出流状态的条件下时，利用闸门上下游液位与闸门开度可以计算得到闸门流量。为快速调控实时流量到达设定目标，需对闸门开度进行适当调节达到合适的范围。进入淹没阶段时，闸门下游和上游形成了相近的液位，此时阀门流量将会受到射流的显著影响，各运行状态下的流速系数选择也会引起计算结果产生偏差，无法达到准确调控的效果；并且处于堰流阶段时，设置不同开度的阀门时并不会造成流量的明显改变。因此分水闸门呈现自由出流的状态，有助于更精确计量与调控闸门流量。为实现闸门的自由出流，本实验通过堰闸结合模式来达到这一控制目标。

根据给定流量Q0与计算流量Q差值ΔQ对目标进行约束控制，计算出目标函数最低值，获得最优闸门开度。以下为目标函数计算式：

将某渠道分水闸门设定在0～0.3 m 的开度内，其宽度等于0.5 m，闸门上游与下游的液位分别位于0.8 m 与0.4 m 的位置，形成了闸孔出流的状态。结合流态判断依据可知，当闸门介于0～0.16 m 的开度范围内时，呈现淹没出流状态，介于0.16～0.3 m之间时，保持自由出流状态，如图2所示。

图2 闸门流态判断Fig.2 Flow pattern judgment of gate

获得闸门的上、下游液位及其开度参数，便可以计算出闸门流量大小。此时用户只需在特定区间中设置合适的流量值便能够利用阀门开度调节模式来完成。为计算出上述条件下的最佳开度值，本研究选择反向学习模式的人工蜂群算法进行处理。对于需求流量的设置，则按照上下游水位进行确定，系统将会设置一个合适的区间，在此范围内调节到合适的流量值，达到闸门开度对流量的准确控制效果。闸门上游液位等于0.8 m 的情况下，处于自由出流的条件下，可以在0.16～0.32 m3/s 的范围实现流量调控功能，如图3所示。

图3 自由出流流态下的流量范围Fig.3 Flow range under free outflow flow pattern

当闸孔保持自由出流的状态时，以设置了反向学习模式的人工蜂群算法经过10 次迭代获得最优解，获得相近的计算和给定流量，同时满足收敛速率的要求，得到图4 的结果。

图4 自由出流状态相关计算Fig.4 Calculation of free flow state

处于自由出流的阶段时，为获得所需给定流量Q0，利用最优闸门开度e获得计算流量Q，可以控制计算和给定流量达到1%以内的误差，可以认为本文算法达到了所需精度标准。结果如表1所示。

表1 计算流量与给定流量关系Tab.1 Calculates the relationship between the traffic and the given traffic

根据表1 可知，利用改进人工蜂群算法进行处理时对于各输入状态都能够计算得到精确闸门开度，确保误差不超过1%，表现出了优异的跟随性能。

3 控制方案

为分水闸门控制过程采用上述算法进行处理时主要是根据给定流量计算合适的闸门开度，之后由控制器按照计算值调节到合适的闸门开度。在人工蜂群算法中加入反向学习后，可以同时满足收敛速率与计算稳定性的要求，符合计算过程的控制需求。但也需注意以上述算法进行处理时需先确定合理的流量来保证后续计算得到准确结果，结合现有环境状态设置合适的流量区。

图5 给出了具体控制原理。将闸门控制在自由出流的状态下时，需要设置堰闸的形式来完成。本次选择曲线外形结构的实用堰，由此获得更高的上游水位，经过以上方式综合处理后使堰顶达到闸孔出流的效果，从而确保下游水位必须比堰体更高的情况下才会引起闸门出流的变化并形成淹没出流。

图5 堰闸系统结构示意图Fig.5 Schematic diagram of weir gate system structure

4 结语

当闸孔保持自由出流的状态时，以设置了反向学习模式的人工蜂群算法经过10 次迭代获得最优解，获得相近的计算和给定流量，满足收敛速率要求。以控制计算和给定流量达到1%以内的误差，可以认为本文算法达到了所需精度标准。

利用改进人工蜂群算法进行处理时对于各输入状态都能够计算得到精确闸门开度，确保误差不超过1%，表现出了优异的跟随性能。

选择曲线外形结构的实用堰，获得更高的上游水位，经过以上方式综合处理后使堰顶达到闸孔出流的效果，确保下游水位必须比堰体更高的情况下才会引起闸门出流的变化并形成淹没出流。