乙炔加氢反应器分布参数动态模拟中空间集总化时滞分析及其对控制性能的影响
程卓欣 许 锋 罗雄麟
(中国石油大学(北京)信息科学与工程学院)
工业过程中,许多系统同时具有时间特性与空间特性,其行为必须依赖时间和空间,这些系统的时空过程被称为分布参数系统[1,2]。国内外学者对分布参数系统的研究大多是利用描述分布参数系统的偏微分方程,运用时空分解思想和模型逼近理论,将分布参数系统转化成集中参数系统来建立模型[3]。 为了方便对分布参数系统进行控制,一般只离散空间变量,保留时间变量,即进行空间集总化。
由于分布参数系统呈现多维甚至无限维特性,这就不可避免地会出现时滞现象,时滞现象会大幅提高建模难度, 目前已报道的分布参数模型大多没有考虑时滞的影响, 导致现有动态模型中各个空间位置状态变量的变化时刻都比实际情况相对提前。 也有学者研究了分布参数系统中的时滞现象,用反馈控制器抵消了部分时滞影响[4]。
乙炔加氢反应器的主要作用是通过乙炔的加氢反应将高浓度乙烯流中的少量乙炔转化为乙烯, 反应器中的多个状态变量同时具有时间特性与空间特性,是典型的分布参数系统。 当反应器入口温度改变时, 反应器内的温度和出口温度不会及时变化, 导致反应器内各个状态变量都不会及时改变。 目前,已有学者建立了乙炔加氢反应器的一维拟均相模型[5,6]、二维非均相模型[7,8]等,但这些模型大多忽略了实际工业生产过程中的时滞现象,导致系统的控制性能下降。 也有学者将所有时滞的总和加入输出变量中, 但是没有考虑每个状态变量的时滞[9]。 由于乙炔加氢反应器有多段床层,时滞现象分布在反应器的各个位置,仅考虑输出变量的时滞往往与现场实际情况有一定误差。虽然已有学者提出带有纯时滞的分布参数系统的PID控制器[10],但是针对动态响应带来容量时滞的分布参数系统的PID控制器还未见报道。
笔者将乙炔加氢反应器现有模型采用有限差分法进行模型逼近[11],获得了便于控制的集总化模型。 对比加入时滞后的时滞精细化模型与不加时滞的现有模型,分析空间集总化对状态变量时滞的影响。 入口温度改变后导致乙炔加氢反应器动态过程长达数分钟, 而时滞往往只有数秒,为了探究短时滞对系统控制性能的影响,用现有乙炔加氢反应器模型设计无时滞PID控制器并应用于时滞精细化乙炔加氢反应器模型中,分析模型与控制器失配情况下,时滞对系统的影响。
1 问题的提出
乙炔加氢反应器同时具有空间特性与时间特性,是具有时滞特性的。 时滞的产生是由于乙炔加氢反应器中存在气体对流,气体对流速度为v,气体从位置z-Δz(Δz为离散的空间步长)处流动到位置z所需的时间τ即为时滞(τ=Δz/v)。 但是,在空间离散化的过程中,学者们忽略了时滞这一特性,造成仿真模型与实际不相符。 因此,笔者在空间集总化过程中加入时滞模块,以逼近实际过程的动态特性。
空间集总化法即保留模型时间变量、离散模型空间变量,在离散空间变量时加入时滞的紧致差分节点如图1所示[12]。 在理想模型下,Δz无限趋近于零,即现有乙炔加氢反应器模型通常默认时滞τ为零,在进行模型逼近时,离散空间所使用结点为B和C。 在实际工业过程中,出于经济等方面的考虑,Δz往往是一个不容忽略的值, 即气体从当前位置流动到下一位置所需的时间τ无法忽略,因此离散空间变量时应使用结点B与C1。
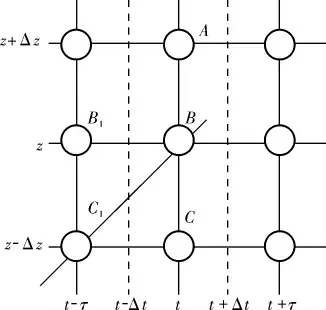
图1 紧致差分格式结点
现场装置的控制回路如图2所示, 若控制器与模型失配,使用现有的无时滞模型设计的控制器直接应用于实际工业现场时,控制系统会振荡甚至不稳定。

图2 装置控制回路
笔者使用针对原模型设计的控制器对时滞精细化模型进行控制,通过仿真结果分析模型存在时滞时对控制效果的影响。 不同控制器对现有模型装置与时滞精细化模型装置的控制效果预测见表1。 使用现有模型装置设计的无时滞控制器在实验仿真中可以获得很好的控制结果,然而将无时滞控制器应用于工业现场时,入口温度每变化一次,时滞都会累积影响到反应器中段和出口温度,控制器的控制周期越短,时滞对系统的影响越大。 想要令控制器直接应用于工业现场,就要针对时滞精细化模型装置来设计时滞控制器。

表1 控制效果预测
2 分布参数系统空间集总化时滞精细化模型的建立与仿真分析
2.1 乙炔加氢反应器模型时滞精细化方法
乙炔加氢反应器是一个典型的分布参数系统,反应器内发生如下反应[13,14]:

乙炔加氢、乙烯加氢以及生成低聚物(绿油)的化学反应本征动力学模型为:

由式(1)~(3)可知,温度T越高,主反应速率r1越快,同时副反应的反应速率r2和r3也会加快。
反应器内各个状态变量同时与时间、空间有关,因此在对乙炔加氢反应器进行建模时,时滞对模型的影响不可忽略。 在建模过程中,考虑流体热量衡算式:

对模型进行精细化修正时,由于反应器半径R较小,所以忽略温度径向对流的时间,仅考虑温度轴向对流的时间;忽略扩散传热的时间,仅考虑对流传热的时间。 催化剂失活周期过长,在较短时间内催化剂活性不发生变化,所以本研究中催化剂活性保持不变。将系统空间长度L划分为m段,空间步长Δz=L/m。 使用泰勒展开对比中心差分、前向差分、后向差分逼近模型的截断误差[15],后向差分的截断误差较小,且隐式差分格式是无条件稳定的[16,17]。 将流体热量衡算式中温度对轴向空间位置求导的偏微分方程进行空间集总化后变换为:

2.2 时滞对状态变量影响分析
以第一床层为例,在反应进行稳态模拟的基础上,将入口气体温度阶跃增加1 ℃,其他操作条件保持不变,观察反应器内加入时滞后各个位置温度变化、出口处乙炔摩尔分率和出口处乙烯摩尔分率的变化,如图3所示。

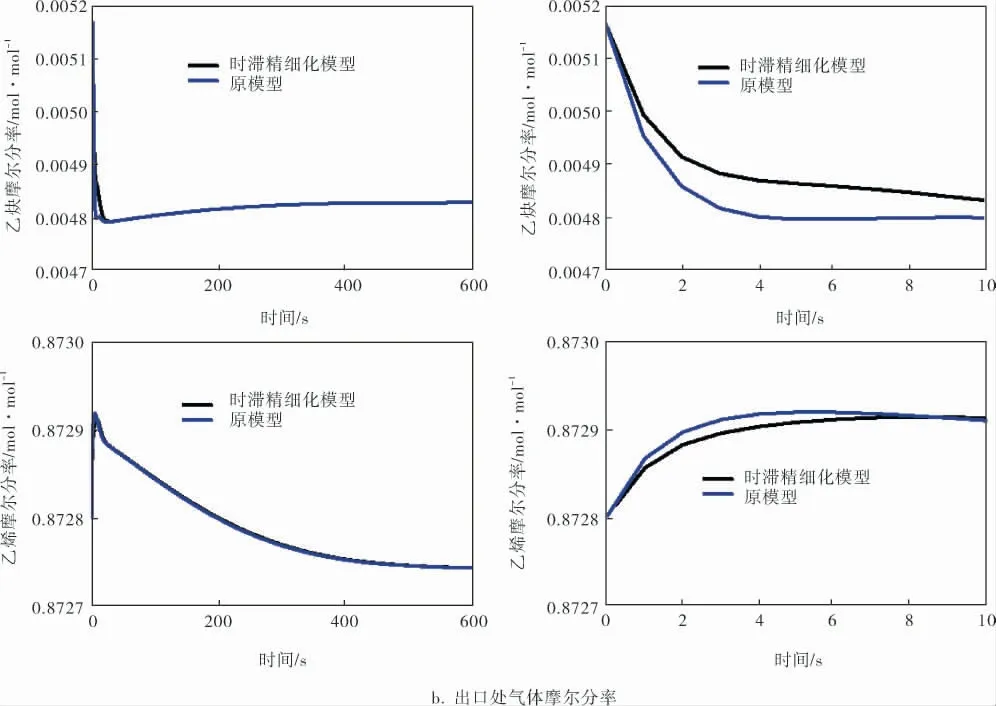
图3 加入时滞的反应器动态响应
由图3a可以看出,将入口处气体温度阶跃升高1 ℃,入口处气体温度无时滞,由于入口处不发生反应,所以入口处固体温度的升高只能通过相间传热,在600 s后升高1 ℃;在入口温度变化后,短时间内精细化模型各个位置的温度会出现纯时滞的现象,由于时滞随着空间位置累加,导致时滞对出口处温度的影响较大。 当系统进入稳态后,乙炔加氢反应器时滞精细化模型中各位置温度会逐渐逼近现有模型温度曲线。
入口处温度阶跃增加导致反应器中部反应剧烈,消耗大量氢气,出口处由于氢气减少,反应速率降低,则放热减少,温度下降,只有当反应器中段的反应热传递到出口,此时副反应乙烯加氢增剧,出口处温度随之上升,致使出口位置温度的变化呈现先上升后下降再上升的趋势。 从图3a可知,反应器中段的气固温差远大于反应器出口处的气固温差。 原因是催化剂活性较高,乙炔加氢反应集中在反应器中段,相间传热阻力导致两相温差较大[18]。
由图3b可得,在整个动态过程中,时滞始终影响着系统状态变量。 出口处乙炔摩尔分率在反应进行到10 s时进入稳态, 此时出口处温度仍在持续上升, 原因是反应进行到10 s后出口处乙炔加氢反应几近停止,而乙烯加氢反应加剧,导致10 s后乙炔摩尔分率不变而乙烯摩尔分率降低。由此得知,在催化剂活性较高的情况下,当前的反应器管长过长,会出现入口温度越高,反应器后段副反应就越剧烈的现象。 因此,当入口温度升高,出口处乙烯摩尔分率反而降低。
在长达600 s的动态过程中,时滞对开环系统的影响并不大。 但是对于闭环系统,在控制回路中,即使很小的纯滞后也会造成稳定性能的大幅下降。 所以,有必要针对此类系统整定常规控制回路参数,改善控制效果。
3 时滞精细化模型装置对常规控制回路参数整定的要求
现有工业乙炔加氢反应器有两个被控变量(出口处温度和乙炔转化率)和两个控制变量(入口处温度、入口处加氢量)[18],控制变量都处于入口,被控变量都处于出口,输入对输出存在较大的滞后,如果使用传统模型,则无法体现这种滞后。 而基于笔者提出的时滞精细化模型设计控制回路的参数,将可以改善控制效果。 本研究选取入口温度作为控制变量,乙炔出口摩尔分率为被控变量。 在实验过程中发现,当控制变量只选取入口温度时,只要入口温度变化趋势相同,则被控变量的选取不影响系统各状态的稳态值。
入口处温度每变化一次,反应器内各位置的温度和出口处温度都会有延迟,由式(5)可得,系统总时滞为mτ,设PID控制周期为CC,则前期控制器会进行mτ/CC次的无效控制后才会进行一次有效控制, 且控制器接收的反馈总存在mτ的滞后,在动态过程中,控制器始终无法收到当前控制效果影响下的反馈值。
使用现有的模型设计无时滞PID控制器输出u(0),整定PID参数,控制第1段床层出口处乙炔摩尔分率达到设定值0.005 130 mol/mol, 同时将无时滞控制器应用于时滞精细化模型。 如果想使加入时滞的模型获得更好的控制效果,就需要重新设计控制器输出u(2),增加时滞控制器中的积分时间,增加的积分时间要大于反应器总时滞,以抵消时滞对出口温度带来的影响,减少系统超调与振荡。 参数整定后不同控制器的PID参数列于表2中。

表2 整定后的控制器参数
由图4所示的控制效果可知, 使用无时滞控制器对时滞精细化模型出口温度进行控制,由于无时滞控制器是基于现有模型设计的,导致控制时出现模型失配的现象,反应器内各段温度变化趋势振荡幅度较大,增加了乙烯的损耗。 使用时滞控制器对时滞精细化模型进行控制,控制效果较模型失配情况下的控制效果好, 振幅减小,系统到达稳态的时间更短。 相比现有模型,时滞精细化模型在模型与控制器适配情况下到达稳态所需的时间更长, 但这种控制效果更加接近实际。

图4 控制效果对比
由图3得知, 入口温度突增会使得反应器中段的反应加剧,消耗大量氢气,出口处反应速率降低,减少反应热。 用PID调节入口温度缓慢上升时,反应器中段也会增加部分氢气的消耗,令反应器后段反应速率变缓,反应热有所降低,然而出口处温度受反应热与传热同时影响, 导致图4中出口处温度在反应前期无明显变化。
4 结束语
乙炔加氢反应器是一个典型的分布参数系统,在空间离散化后,气体的流动会体现为状态变量间的滞后,入口变量发生变化后,通过状态变量滞后的累积, 体现为输入对输出的较大滞后。 当前应用广泛的乙炔加氢反应器模型缺少对这种时滞的考量,基于现有模型设计的控制器偏离实际生产,应用于工业现场中会造成系统较大幅度振荡,且控制器的控制周期越短,振荡幅度越大。 本研究针对时滞精细化模型改进了PID控制器的参数,通过增加积分时间,削弱了滞后的影响,仿真结果获得了较好的控制效果。

