路网时窗排序的回归模型树轨迹索引
韩京宇,陆 维,武 凡,刘 阳,葛 康,朱 曼,陈 伟
1(南京邮电大学 计算机学院,南京 210023)
2(江苏省大数据安全与智能处理重点实验室,南京 210023)
1 引 言
随着车载传感网、智能手机和移动计算技术的飞速发展,大量轨迹数据源源不断地产生,构成智能交通、智慧城市的基础信息源.高效的轨迹数据查询和分析是支撑应用的关键,这依赖于有效的时空数据索引结构[1-3].轨迹数据查询根据目标时间分成3大类,即未来、当前和历史查询[1,4].本文重点关注历史轨迹数据的查询,它是各种轨迹查询和分析的基础.支持历史轨迹查询的索引分成基于时空划分的、基于数据划分的和基于映射的方法.第1类方法直接对时空进行划分,不考虑数据的聚簇性,如KDB树[5,6]、SWST(Sliding Window Spatio-Temporal)索引[7]等.第2类方法根据数据的临近性来划分索引节点,以R树的变体为代表,如MV3R-Tree[8],DSTR-Tree[9],T-PARINET[10]等.第3类基于映射的方法把多维时空数据降维后进行查询.如根据希尔伯特(Hilbert)曲线、Z曲线等降维后支持查询[11,12].传统索引的主要问题在于,为了支持细粒度的查询,索引大小随数据量增长,降低查询性能.同时,以树为主的多维索引结构由于节点覆盖区域重叠,一个查询会牵涉多个搜索路径,查询性能不尽如人意.
针对传统索引的问题,最近的学习型索引提供了全新的解决思路[13,14],即通过机器学习训练键和存储位置的映射模型,取代传统的索引结构,不仅可以减少空间占用,而且可以保障及时的查询响应[15].多维数据学习型索引的性能主要依赖于模型选择和数据布局[16,17].根据数据布局策略的不同,多维数据学习型索引分成布局决定模型和模型产生布局两大类.前者先基于一定的顺序如希尔伯特,Z-order顺序,确定多维点的一维顺序,然后根据这个数据布局训练从数据到存储位置的预测模型[18-20];后者首先确定数据布局模型,然后根据这个模型来放置数据[21].
多维数据的学习型索引并不完全适用于支持历史轨迹的查询[18],原因在于:1)轨迹点是路网时空中的点,路网和时间维度呈现不同特性,存储顺序要兼顾轨迹点的路网邻近性和时间临近性;2)不同时空范围的数据疏密程度差异巨大,个别稀疏区域的点会扭曲预测模型的精度,需要寻找适应不同区域数据分布的模型;3)需要寻找有效的索引维护方法,保证预测精度的前提下,降低数据插入时的维护代价.
针对轨迹数据,提出了一种基于路段时窗排序的回归模型树(Regression Model Tree,RMT)以支持历史轨迹数据查询,分两阶段构建.第1阶段,轨迹点在路段时窗空间进行优化排序:第1步,结合希尔伯特曲线和路网连通性,通过组合优化算法,发现最优的路段排序;第2步,根据路段排序,通过双层划分来确定轨迹点的序号,上层保证所有路段时窗区域的一维顺序,下层保证每个局部区域轨迹点的优化顺序.第2阶段,历史数据被划分成若干周期,提出了两种训练存储位置预测模型的模式,一种是批量加载模式,即对每个周期训练一个单独的回归模型树来预测轨迹点的存储位置;一种是周期更新模式,采用间隙数组来存储所有周期的轨迹点,只训练初期的模型,后续周期的数据在数组的预留位置插入,从而避免多次训练模型.
本文的主要贡献如下:
1)提出了一种分层的轨迹点排序方法,上层根据路段连通性划分区域,下层根据路段内的时空邻近性来优化轨迹点排序,保证存储顺序和轨迹点的时空连续性一致.
2)采用回归模型树对数据的存储位置进行建模,在树的叶结点使用模型拟合局部数据分布,不仅能适应不同的数据分布,而且减少树的层数,降低模型复杂度.
3)在周期更新模式中,提出采用密度依赖间隙数组来存储数据,采用AdaBoost训练存储位置预测模型[22],提高精度的同时,保证模型泛化性,避免训练各期数据.
2 相关工作
2.1 多维数据索引
多维数据索引方法分为基于数据划分和基于空间划分的两大类.基于数据划分的方法根据数据的聚簇来组织索引节点,让邻近的数据放在相同的节点,主要以R树及其变体为代表[23,24].R树是一个多维的平衡树,能够支持数据的动态插入和删除.数据在R树中的节点,不仅受本身坐标的影响,而且受插入顺序的影响,为了减少节点覆盖的死空间(dead space),紧凑R树(packed R-tree)采用批量加载解决这个问题[24].为了减少目录覆盖重叠,降低查询的多路搜索代价,R*树每次选择使目录重叠最小的节点进行数据插入[25].
基于空间划分的方法递归地对嵌入数据的空间进行划分,直到每个划分中的数据量在一个叶节点可以容纳.网格文件(grid file)是典型的基于空间划分的索引[26],空间划分成单元格,查询时通过目录映射到对应的桶,寻找数据.另外k-d树[5]和四岔树(Quad tree)[27]也是检索多维数据的常用索引.k-d树是检索k维空间点的二叉树.由于索引层级多,并且不平衡,为此K-D-B树[6]用B+树和k-d树结合,实现索引平衡.四叉树作为一种树结构,每一个节点递归地划分成4个子树,其主要弱点是,数据层数比较多,不能保证树的平衡[27].
2.2 历史轨迹数据索引
移动对象的轨迹点是路网时空中的多维点.为支持点查询、范围查询和kNN(k-Nearest Neighbour)查询,其索引分成3类,即基于数据聚簇的、基于时空划分和基于映射的方法.
基于数据聚簇的方法根据轨迹点的邻近性来创建索引节点,以R树及其变体为代表.MV3R-Tree支持历史时空数据查询[8],使用一个多版本的R树和一个3维R树的组合来索引时空数据.SETI(Scalable and Efficient Trajectory Index)采用两层索引结构,将空间和时间分开,索引从过去到最近的移动对象位置[28].
基于时空划分的方法直接对时空进行划分,不考虑数据的聚簇性.SWST(Sliding Window Spatio-Temporal)是一种基于磁盘的两层滑动窗口索引[7],它将区域划分成不重叠的单元格(cell),每个单元格都有一个时间索引,该索引由两棵B+树组成,分别对应不同的时间范围.基于布隆过滤器(Bloom Filter)的轨迹查询方法首先对时空按照网格划分,每个单元格被分配一个独立的地理编码.每个单元格中的点被视为一个签名(signature),形成到布隆过滤器的位数组映射,从而查询到对应的轨迹段[29].
基于映射的方法首先将多维数据降维,进而索引定位.通常在多维空间中寻找有效的空间填充曲线,如希尔伯特曲线、Z-order曲线等[11,3,12]实现空间转换.希尔伯特曲线方法用每个路段的中点代表整个路段,然后根据希尔伯特曲线排序,确定各个路段的一维序号[11].文献[3]将时间和空间维度分离,通过希尔伯特曲线对空间坐标分配唯一序号,把时间当作另外一个维度,构建一个二维的R树来索引时空轨迹点.文献[12]采用Z曲线顺序将含多个属性的数据按序存储,从而加快范围查询.
2.3 学习型索引
学习型索引把索引看作键和存储位置的映射模型[13],根据目标数据的维度,分成一维学习型索引[13,15,30,67]和多维学习型索引[18-21].
一维数据的学习型索引,根据模型构建顺序,分成自上而下和自下而上两类方法.自上而下的方法,如采用递归模型索引(Recursive Model Index,RMI)取代B-Tree[13].它自上而下,迭代求精,逐层减小训练误差.自下而上的方法,如RadixSpline策略[30],首先扫描所有的数据点,根据误差阈值确定一系列的折线段点(spline point),然后在折线段点上构建基数表(radix table),以支持对折线段的快速定位.分段几何模型(Piecewise Geometric Model,PGM)也是采用自下而上的方式逐层构建模型[31].
多维数据学习型索引的效果主要取决于数据布局和模型选择,可分成布局决定模型和模型产生布局两大类方法.第一类方法,先基于一定的顺序如希尔伯特、Z-order顺序等确定各个轨迹点的顺序,然后根据这个排序训练从数据到存储位置的映射模型[18-20].RSMI(Recursive Spatial Model Index)方案首先根据Z曲线确定各个轨迹点的序号,然后再训练多层感知机(Multi-Layer Perceptron,MLP)以支持空间数据查询[18].ZM(Z-order Model)首先确定Z曲线,然后分阶段训练模型,其中每层是神经网络或者是线性模型[19].文献[20]用ML(Multidimensional Learned)索引支持多维数据查询.为了寻找全序,首先选定若干个参考点,每个数据相对于最近的参考点计算距离,从而为每个数据点在距离空间分配唯一的序号.第二类方法,首先确定数据布局,根据这个布局放置数据,然后在此基础上训练模型,以LISA(Learned Index for Spatial dAta)为代表[21].LISA首先构建一个偏序函数实现键值到一维顺序值的映射,然后学习一个单调的、由分段线性函数构成的碎片(shard)预测函数,负责把映射后的空间分割成碎片.然后在每个碎片中构建本地模型把碎片所属的数据组织成块.最后根据学得的模型来安排数据的存储布局.
3 问题描述和轨迹点排序
3.1 问题描述和方法概述
每个移动对象在路网上运动,向数据中心发送轨迹点.
定义1.(路网)路网是路段和交叉口的图,记为NT=(V,E),其中V是交叉口集合,E是路段集合.
定义2.(轨迹点)轨迹点是一个三元组,记为le=(x,y,t),其中x是经度,y是纬度,t是时间戳.
本文中时间轴被划分成一系列等长的周期

表1 论文中使用的关键符号
定义3.(路段时窗网格)给定时窗长度r,路段时窗网格沿路段E和时窗T建模,记为RW=(E,T),E是所有路段的集合,T是所有时窗的集合,每个时窗t∈T持续时长r.
给定轨迹点集合D,要支持两种基本查询,即点查询和范围查询,这两种查询是其它查询和分析的基础.
·给定点查询q(x,y,t),返回D中与(x,y,t)具有相同坐标的轨迹点.
·给定范围查询q(sr,dr),其中sr=[(x1,yb),(xr,yt)]表示目标空间矩形的左下角和右上角坐标,dr=[t1,t2]表示目标时间窗口,返回结果是被sr和dr包围的轨迹点集合.
为了支持最近时间以前的历史数据查询,每经过一个周期Pj,对所有属于Pj的轨迹点建立索引,以支持点查询和范围查询.首先对所有的轨迹点进行映射,获得一维的全局序号;然后,按照两种模式构建轨迹点的存储位置预测模型,即批量加载模式和周期更新模式.对于批量加载模式,每个周期的数据单独训练,学得一个模型支持该周期的数据查询.对于周期更新模式,采用密度依赖间隙数组存储各期数据,由于各期数据符合相同的数据分布,在P0周期训练预测模型,以后各期数据根据预测插到间隙位置.
3.2 计算轨迹点的全局序号
每个轨迹点在路网时空产生,先用唯一的标识符指示每个路段,然后将所有轨迹点映射到路段时空,从而确定轨迹点的全局序号.
中小企业的划分标准是由国务院负责企业工作的部门根据企业职工人数、销售额、资产总额等指标,结合行业特点制定,对于不同的行业,划分标准也有所不同。中小企业大多雇用人数与经营额都不大,多数上由业主直接管理。[1]其特点主要包括:经营产品单一,风险较高;所有权与经营权很难分离;会计及内部控制从业人员素质较低。
3.2.1 计算路段的全局序号
路段映射应使两个相邻路段的序号尽可能靠近,通过两步获得:采用文献[11]的方法初始化路段排序,然后通过模拟退火来优化排序[32].初始排序通过如下步骤完成:1)在欧几里得空间中,用路段的中点表示每个路段;2)构建覆盖所有点、分辨率足够细的网格,确保网格的行列相等,并且每个点都落入唯一的网格单元;3)将网格用一条遍历所有单元的希尔伯特曲线填充,每个点获得唯一的希尔伯特曲线序号,根据曲线序号排序,获得每个路段的初始序号.
该路段排序给出了欧氏空间中的排序,但个别相邻的网格单元可能希尔伯特序号并不邻近[33],同时没有考虑路网连通性.为了进一步优化路段排序,定义路段距离:
定义4.(路段距离)给定NT中的两条路段e1和e2,其路段距离jd(e1,e2)是连接路段e1和e2的最短路径中包含的交叉口数目.
一个路段不同程度的邻近路段集合用m阶邻边集定义:
定义5.(k阶邻边集)一个路段e的m阶邻边集是路网上与e的路段距离等于或小于m的路段的集合,记为mN(e).
给定路段排序IS,设路段e的序号为rn(e),其排序误差是
se(IS)=∑e∈IS∑j∈mN(e)|jd(e,j)-dif(e,j)|
(1)
其中,jd(e,j)是e和j的路段距离,dif(e,j)=|rn(e)-rn(j)|.要优化IS,使式(1)达到最小,保证路段在路网上的距离和序号距离尽可能接近.这是一个NP问题,采用模拟退火来解决.为支持对m阶邻边的快速查找,建立一个倒排表NIL(np,jd)存储每个路段的所有m阶邻边,其中np是路段对,jd(jd≤m)是它们的路段距离.整个过程如算法1所示:
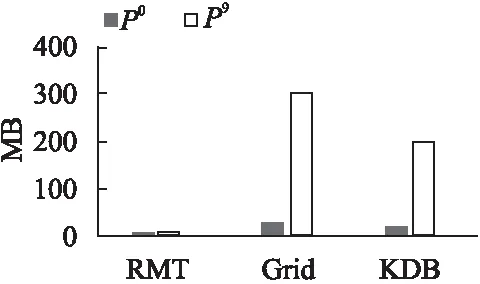
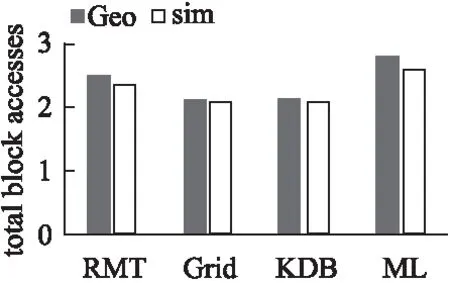
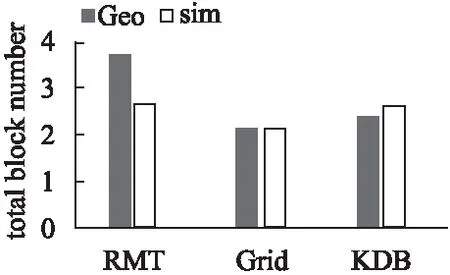
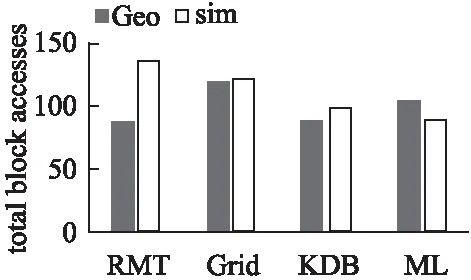
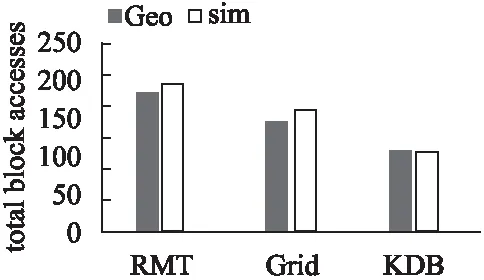
输入:基于希尔伯特序号的初始路段排序IS,m阶邻边表NIL,初始温度tl(tl>0),冷却率cr(0 输出:优化的路段排序 1.while tl>0 do 2.S←randomly choosesspositions fromIS; 3.foreachiinSdo 4.produceISnewby interchangingIS[i]andIS[i+1]; 5.θ←se(IS)-se(ISnew); 6.ifθ>0 then 7.IS←ISnew; 8.end 9. else 10.p←exp(-θ/tl),pth←random(0,1); 11.ifp>pththen 12.IS←ISnew; 13.end 14. end 15. end 16.tl←cr×tl; 17.end 18. returnIS; 该算法的基本思想是,优化后的排序中尽量保持所有路段对间的路段距离.算法的时间复杂度为O(ss×logcrtl),其中tl是初始温度,cr是冷却率,ss是每个温度阶的大小. 3.2.2 确定轨迹点的全局序号 采用隐马尔可夫模型(HMM)[34]将每个轨迹点映射到对应的路段.为获得轨迹点在路段上的序号,按照如下规则确定路段起始点:给定路段两个端点的坐标,选择x坐标小的路段端点为起始点;如果x坐标相同,则选y坐标小的端点为起始点.这样,每个匹配到路段的轨迹点le有唯一的路段位置坐标,记为sp(le)=(ei,off),其中ei是路段序号,off是轨迹点相对起始点的规范化偏移量,满足0≤off≤1. 给定一个轨迹点,提出采用两层策略确定它的全局序号(global order number,gon).第1层,通过水平或垂直合并相邻的路段时窗单元格,以获得行列数目相等的融合路段时窗网格,进而根据希尔伯特排序,每个融合单元格获得一维编号,这个序号同时兼顾了欧式空间的邻近性和路网连通性.第2层,在每个融合单元格内采用G树排序编码方法[35],获得融合单元格内所有轨迹点的局部序号.结合第1层的融合单元格序号和第2层的局部序号,获得所有轨迹点的全局序号. 1)构建融合路段时窗网格 合并路段时窗网格的单元格,形成融合路段时窗网格. 定义6.(融合路段时窗网格)给定路段时窗网格RW=(E,T),其融合路段时窗网格MRW=(ME,MT),每个me∈ME对应E中的一个或多个路段,每个mt∈MT对应T中的一个或多个时窗.同时,|ME|=|MT|=2i(i∈N并且i>0). 使用算法2构建融合路段时窗网格.它首先沿路段维度划分单元格,然后沿时间维划分,最终形成行列数目相等的融合路段时窗网格. 算法2.mergedSegmentTimeGrid 输入:路段时窗网格RW=(E,T) 输出:融合路段时窗网格MRW=(ME,MT) 1.m←|E|,n←|T|; 2.fl←the largest integer satisfyingfl=2iandfl≤min(m,n); 3.r1←⎣m/fl」,k1←mmodfl; 4.forj←0,j 5.ifj 6.ME[j]=E[j×(r1+1),…,(j+1)×(r1+1)-1]; 7.end 8. else 9.ME[j]=E[k1×(r1+1)+(j-k1)×r1,…,k1×(r1+1)+(j-k1+1)-1]; 10.end 11. end 12.r2←[n/fl],k2←nmodfl; 13.forj←0,j 14.ifj 15.MT[j]=T[j×(r2+1),…,(j+1)×(r2+1)-1]; 16.end 17. else 18.MT[j]=T[k2×(r2+1)+(j-k2)×r2,…,k2×(r2+1)+(j-k2+1)-1]; 19.end 20. end 21.MRW←(ME,MT); 22.returnMRW 该算法对路段时窗分别遍历,因此时间复杂度是O(m+n),其中m、n分别代表路段时窗网格的行列数目. 一旦确定了融合路段时窗网格,根据希尔伯特空间填充曲线为每个融合路段时窗网格单元MRW[i,j]确定一个希尔伯特序号,记为hn(MRW[i,j]). 2)确定轨迹点序号 首先,在每个融合单元格中确定轨迹点的局部序号,然后根据局部序号和每个合并单元格的希尔伯特序号确定全局序号. 定义7.(局部序号)给定一个轨迹点le,其局部序号lon(le)是其在融合路段时窗单元MRW[i,j]中的序号. 按照如下步骤获得局部序号:由于每个轨迹点le都有一个路段位置坐标sp(le)=(ei,off),先对所有路段序号排序,然后对具有相同的路段序号的轨迹点按照off进行排序,从而获得每个轨迹点唯一的融合位置编号mln(le).因此,所有轨迹点都嵌入在由融合位置编号和时间组成的二维空间中.进一步,在每个融合单元格中计算局部序号,包括分区和编码序号生成两步: 1)分区:在位置时间空间中交替沿两个维度划分,每次把原区间均分,直到每个分区最多有一个轨迹点.对于每次分割,左侧(或底部)区域编码为0,右侧(或顶部)区域编码为1.根据划分顺序,从左到右拼接所有对应的0或1,形成每个划分对应的位串. 2)编码序号生成:每个轨迹点用对应的位串表征.设最大位串长度为m,对于长度小于m的位串bs,在位串的右端拼接m-s个0,其中s是bs的长度,从而使所有轨迹点对应等长的位串.位串对应的十进制数就是轨迹点的局部序号.注意,相邻的局部序号间是有空隙的. 全局序号(gon)按照如下定义确定. 定义8.(全局序号)给定一个轨迹点le,其全局序号gon(le)递归计算如下:1)若hn(MRW[i,j])=0,其中MRW[i,j]是le所属的融合路段时窗单元格,le的全局序号和其局部序号相同;2)设MRWpre是le对应的融合路段时窗单元的前一个单元格.如果MRWpre中轨迹点的最大全局序号为n,则le的全局序号为n+lon(le). 每个周期创建一个新的回归模型树,支持本周期数据的查询. 每个周期Pi建立一棵回归模型树(Regression Model Tree,RMT),它不同于分类回归树(Classification And Regression Tree,CART):首先,叶子节点使用线性函数,而不是常数值,来拟合数据分布.其次,当拟合误差低于给定阈值时,分裂停止.其优点在于:1)能够适应不同的数据分布,减少树的层数和模型节点数;2)提高每个叶节点的拟合精度.具体来说,给定一个含n个样本{le0,…,lei,…,len-1}的内部或叶节点tn及模型M,节点的拟合误差是: (2) 其中yi是lei的存储地址,M(lei)是预测存储地址. 采用排序数组来存储所有轨迹点.给定n个轨迹点,如果直接根据它们的全局序号排序,它们的存储地址范围是[0,n-l].然而,由于数据分布倾斜,个别稀疏区域的孤立点会扭曲拟合模型.为了解决这个问题,提出在排序数组中保留少量间隙进行平滑.为此,定义前向间隙如下: 定义9.(前向间隙)将所有轨迹点样本按照全局序号进行排序 给定所有轨迹点的排序 训练回归模型树时,每个样本的输入是(x,y,t),输出是其存储地址addr(x,y,t).回归模型树递归分割数据,并在每个分区内拟合线性函数.对于每次分割,必须确定分割维度j和分割点s.每次分割成两个划分R1(j,s)={le|le.j≤s}和R2(j,s)={le|le.j>s},分割元组(j,s)须满足 minj(mins(∑le∈R1wle·(addr(le)-M(le))2+(∑le∈R2wle·(addr(le)-M(le))2)) (3) 其中wle是样本le的权重(默认是等权重);M是线性函数 M(le)=θ0+θ1·le.x+θ2·le.y+θ3·le.t (4) 其中θ0、θ1、θ2、θ3是待拟合的参数.给定最大误差阈值eb,当误差低于eb时,分裂停止. 给定点查询q(x,y,t),假设RMT(x,y,t)=pt.在[pt-eb,pt+eb]中搜索排序数组,找到与(x,y,t)具有相同坐标的样本作为查询结果.给定一个范围查询q(sb,tr),其中sb=[(xl,yb),(xr,yt)]表示目标空间,tr=[t1,t2]表示目标时间.根据sb和tr,可以得到时空立方体的8个顶点(xl,yb,t1),(xl,yt,t1),(xr,yb,t1),(xr,yt,t1),(xl,yb,t2),(xl,yt,t2),(xr,yb,t2),(xr,yt,t2).根据RMT,它们映射到8个存储地址(pt1,…,pt8).进而,在[min{pti-eb|1≤i≤8},max{pti+eb|1≤i≤8}]内搜索过滤,可以得到查询答案. 提出基于间隙数组一次提升(Gapped-Array based Boosting-once,GAB)的周期更新模式:采用密度依赖间隙数组存储所有周期的数据;用P0的数据训练预测模型,该模型兼容未来周期的数据插入,具体论述如下. 定义10.(密度依赖间隙数组)给定期望的周期数L和预分配比例因子a(a>1),密度依赖间隙数组是一个与L、a和每个样本密度1/fg(lei)成比例地预分配空槽的数组. 具体来说,设P0的所有样本根据全局序号的排序是 addr(lei)=∑j (5) 其根据样本密度为将来的插入腾出空间:a越大,预分配的空槽越多;fg(lei)越小,lei周围的样本密度就越大,在样本周围分配更多的空槽.一旦分配了整个间隙数组的存储空间,在P0数据上使用Adaboost训练含多个回归模型树的集成模型,各个周期的数据插入和查询都根据集成模型来预测存储位置,不仅可以提高预测精度,而且避免单个模型过拟合的问题. 在P0的数据上训练集成模型的步骤如算法3所示. 算法3.boostTraining 输入:Training dataD,segment-time gridRW,the number of regression model treesk 输出:An ensemble model{ (M1,w1),…,(Mk,wk)} 1.initialSampleWeight(D,RW); 2.for(i←1 tok) 3.{ 4.derive modelMiwithDi; 5.compute the error factoref(Mi)according to Equation (8); 6.for(j←1 to |D|) 7.{ 9.} 10.w(Mi)←ln(1/ef(Mi)); 11.} 12.return{(M1,w(M1)),…,(Mk,w(Mk))}; 第i次迭代中每个样本lej的相对误差 ei,j=(|yj-M(lej)|)/max{|yj-M(lej)‖lej∈D} (6) 模型Mi的误差为: (7) Mi的误差因子是: ef(Mi)=err(Mi)/(1-err(Mi)) (8) 每次迭代期间,每个样本lej的权重更新为: wi+1,j=(wi,j/Zi)·ef(Mi)1-ei,j (9) 在训练模型中,应确保每个有数据的单元格都被采样,并且采样率与单元格内样本的密度成正比.另外,根据全局序号排序时,若样本与其前后样本的全局序号差较大,则指示该样本周围数据少,要加大该区域样本被采样到的概率,提高模型精度,算法4给出样本的初始权重确定方法. 算法4.initialSampleWeight 输入:Training datasetDwith every sample′s segment-time cell identifier,segment-time gridRW 输出:Weights of all the samples 1.initialize the weight of every sample to be 1/|D|; 2.for(i←0 to |RW.E|-1) 3.{ 4.for (j←0 to |RW.T|-1) 5.{ 6.if(RW[i,j] has data) { 7.ws[i,j]←0; 8.gs[i,j]← 0; 9.foreach(le∈RW[i,j]) 10.{ 11.ws[i,j]←ws[i,j]+le.w; 12.gs[i,j]←gs[i,j]+log2(fg(le)+fg(follow(le))); 13.} 14.forEach(le∈RW[i,j]) 15.{ 16.le.w←ws[i,j]×(log2(fg(le)+fg(follow(le)))/gs[i,j]); 17.} 18.} 19.} 20.} 21. return all the samples with their weights; 算法4中,follow(le)表示根据全局序号紧跟le的样本. 训练完成后,获得了一个集成模型PM={(M1,w1),…,(Mk,wk)}.给定一个样本le,其存储地址预测为 (10) 最后,在D上统计最大误差阈值eb,在后续周期插入时,如果超过了这个误差阈值,要修改eb. 当一个新的轨迹点在Pi(i≥1)期到达时,首先调用预测模型返回一系列预测地址(pt,p1,…,pi,…,pk).其中,pt是集成模型的预测结果,而pi是第i个回归模型树的返回结果.将轨迹点放置在尽可能接近pt的空槽,从而降低未来的查询代价,具体步骤如算法5所示:如果pt位置已经占用,将p1,…,pi,…,pk中不同的地址按照模型的累加权重降序排序,选择最靠前的空位置插入样本. 算法5.incrementalInsertion 输入:预测模型PM,轨迹点le,密度依赖间隙数组DY,最大误差阈值eb 输出:le的存储地址 1.(pt,p1,…,pk)←PM(le); 2.ifDY[pt]is empty then 3.placeleatDY[pt]; 4.returnpt; 5.end 6. else 7.SS←SortingByWeights(PM,(p1,…,pk));//降序排列 8.fori←0 to |SS| do 9.addr←SS[i]; 10.ifDY[addr]is empty andaddris in[pt-eb,pt+eb]then 11.placeleatDY[addr]; 12.returnaddr; 13.end 14. end 15.if there is no qualified address then 16.pnew←find an empty slot nearest topt; 17.placeleatpnew; 18.ifpnewis outside[pt-eb,pt+eb] then 19.updateebwith the enlarged error bound; 20.end 21. returnpnew; 22.end 23. end 如果误差阈值范围内的预测位置全部占满,则寻找离pt最近的空位置pnew插入,如果|pnew-pt|超过eb,就需要修改eb.由于集成模型调用时,在内存中进行.算法的复杂度主要取决于搜索时的磁盘I/O数目,设一个外存块存储B个数据点,则算法的时间复杂度为O(eb/B). 给定一个点查询q=(x,y,t),调用算法6回答. 算法6.pointQueryEnsemble 输入:密度依赖间隙数组DY,点查询q=(x,y,t),最大误差阈值eb,预测模型PM 输出:DY中和(x,y,t)具有相同坐标的轨迹点 1.(pt,p1,…,pk) ←PM(q); 2.rg←[pt-eb,pt+eb]∩[min(p1,…,pk),max(p1,…,pk)]; 3.ret←scanrginDYto find the position which has the same coordinate asq; 4.returnret; 算法先在内存对模型访问,然后访问数组,时间主要由访问外存的磁盘I/O决定,最坏情况的时间复杂度为: O(2×eb/B)=O(eb/B) 给定一个范围查询,用算法7来回答. 算法7.rangeQueryEnsemble 输入:密度依赖间隙数组DY,范围查询q(rr,tr),最大误差阈值eb,预测模型PM 输出:满足要求的轨迹点 1.ret←0,RG←[],S←rr×tr; 2.foreach tuplevt∈Sdo 3.(pt,p1,…,pk) ←PM(vt); 4.rgvt←[pt-eb,pt+eb]∩[min(p1,…,pk),max(p1,…,pk)] 5.RG←RG∪rgvt 6.end 7.foreach samplelefound by scanningRGdo 8.ifleis enclosed byrrandtrthen 9.ret←ret∪{le}; 10.end 11. end 12. returnret 时间复杂度主要取决于磁盘访问的I/O,共要访问8个区域,每个区域的最大长度是2·eb,最坏的情况下要8个I/O,因此时间复杂度是O(16·eb/B)=O(eb/B). 实验在一台32核处理器(Intel Xeon,2.83GHz)和64GB RAM的台式机上运行,程序使用Python实现.轨迹数据存储在外存上,每个外存块存储 1000个轨迹点,即B=1000.提出的回归模型树RMT与以下工作进行了比较. K-D-B-Tree(KDB)[6]:作为k-d-Tree的一维版本,结合了k-d-Tree和B-Tree的优点,以获得平衡搜索深度. ML-Index(ML)[20]:ML-Index是一种支持点、范围和k-NN查询的多维学习(Multidimensional Learned)型索引.它选取若干参考点,数据相对参考点计算距离,从而映射到一维空间进行索引和查询处理. 实验使用真实和模拟轨迹数据集.真实轨迹来自Geolife项目[36],选取了北京市的公交、汽车和出租车轨迹,共计1200万个点,代表了有偏斜的数据分布,记为Geo.模拟数据通过调用Brinkhoft移动对象生成器产生[37],记为sim.路网使用www.openstreetmap.org网站提供的北京四环内的道路,由17948个节点和27036个边组成.按照如下规则生成均匀分布的2000万个轨迹点: 1)所有路段的限制最大速度分为6类,所有移动对象的最大速度分为3类.模拟移动对象的运行速度要小于该移动对象类的速度限制和路段类的速度限制. 2)在路网上根据均匀分布选取一个位置作为轨迹起点,结束位置按照同样规则确定. 3)共生成5000个移动对象,每个移动对象采样4000次,每秒采样一次. 在每个数据集上,分别生成500个点查询和500个范围查询.除特别说明,RMT的最大误差阈值是1000,周期更新模式中划分从P0~P9共10个周期,Adaboost策略中选取k=5.汇报的是6次实验的平均值. 6.1.1 批量加载模式下方法的比较 Geo和sim数据集分成10个周期.对于批量加载模式,每个周期构建一个索引模型.图1比较了RMT、Grid、KDB和ML各周期索引的平均大小.由图1的结果可知,RMT索引远小于传统索引Grid、KDB和学习型索引ML:在Geo数据集上,RMT的大小是Grid的1/131,是KDB的1/88,是ML的1/14;在sim数据集上,RMT是Grid的1/92,是KDB的1/83,是ML的1/15.这主要由于RMT的每个叶节点用模型拟合不同的数据分布,能容纳更多的轨迹点,从而减少树的深度和大小.ML学习型索引采用神经网络,耗费空间要大于RMT. 图1 批量加载模式中索引大小的比较 6.1.2 周期更新模式下方法的比较 对于周期更新模式,在P0周期数据上建立索引,后期索引进行增量维护.由于ML没有给出增量插入方法,不和该方法比较.图2报告了在Geolife数据集上,P0周期末RMT,Grid,KDB的索引大小和P9周期末RMT、Grid、KDB的索引大小.在周期更新模式中,RMT的Adaboost策略选取k=5,即包含5个回归模型树.从图2可以看出,P0周期末,Grid和KDB的大小分别是RMT大小的4.3和2.9倍. 图2 周期更新模式中的索引大小比较(Geolife) 在P9周期末,Grid和KDB的大小分别是RMT的41.8倍和28.4倍.这是因为RMT采用间隙数组,在P1~P9周期中,索引不增大,而Grid和KDB会随着数据的插入而增大. 以下比较不同方法的点查询和范围查询的外存访问块数,这是影响查询响应时间的主要因素. 6.2.1 点查询访问块数比较 图3报告了在批量加载模式下,两个数据集上点查询的平均访问块数的比较.可见RMT的平均访问块数略高于Grid和KDB,这是由于RMT索引节省空间,但近似误差会导致搜索块数的少量增大.但相比于同类的ML索引,RMT由于通过叶子节点的模型拟合数据分布,提高了预测精度,平均访问块数要少10%. 图3 批量加载模式中点查询访问块数的比较 图4比较了周期更新模式下点查询的平均访问块数.可见在均匀分布的sim数据集上,RMT的外存访问块数和Grid和KDB基本持平;在倾斜分布的Geo数据集上,RMT访问的块数要多于Grid和KDB,主要因为在周期更新模式中,RMT在维护周期不再训练模型,倾斜大的数据会导致误差阈值变大,要搜索更多的块. 图4 周期更新模式中点查询访问块数的比较 6.2.2 范围查询性能比较 下面比较平均外存访问块数.对于周期更新模式,所有查询在最后一个周期末执行.由于ML没给出增量插入策略,在周期更新模式下,不和ML比较. 图5和图6分别报告了在批量加载模式和周期更新模式下,范围查询的平均外存访问块数.从图5可知,在批量加载模式下,RMT的访问块数和其它几种方法完全可比.从图6可见,在周期更新模式下,RMT的平均访问外存块数要小幅高于Grid和KDB.主要因为RMT的周期更新策略,在后期数据插入时,误差阈值的维护,会带来搜索范围的扩大. 图5 批量加载模式中范围查询访问块数的比较 图6 周期更新模式中范围查询访问块数比较 随着大数据、通讯技术的飞速发展和移动设备的普及,轨迹数据查询和分析的需求无处不在.轨迹索引作为支撑查询的核心技术,面对源源不断的数据,如何降低索引大小,保障查询效率是焦点.近几年,结合机器学习技术,采用学习型索引改进传统索引受到广泛关注,但时空数据由于其维度的不同性质和普遍存在的数据倾斜,设计适合路网时空数据查询的学习型索引亟待研究.本文提出了一种基于路段时窗排序的回归模型树,可以有效地支持路网轨迹数据查询.本文的主要意义在于: 1)提出回归模型树索引,在保证查询精度的同时,可以大幅度降低轨迹数据索引的空间代价,这对智慧城市、智能交通中的巨量轨迹数据管理意义深远; 2)提出一种新的基于Adaboost的学习型索引增量维护方法,在基于密度依赖的间隙数组的支持下,只需要训练一次模型,大大降低了索引维护代价.在真实和模拟数据集上的实验表明,相比于传统索引,不仅大大减少了存储空间,而且查询性能完全可比;相比于同类的学习型索引,具有更少的空间占用和更优的查询性能.后续工作将研究通过捕捉数据分布模式,降低查询代价.4 批量加载模式和查询
4.1 回归模型树训练
4.2 点查询和范围查询
5 周期更新模式和查询
5.1 基于初始周期数据训练集成模型
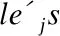
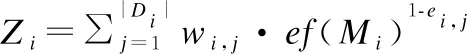
5.2 未来周期数据的增量插入
5.3 点查询和范围查询
6 实 验
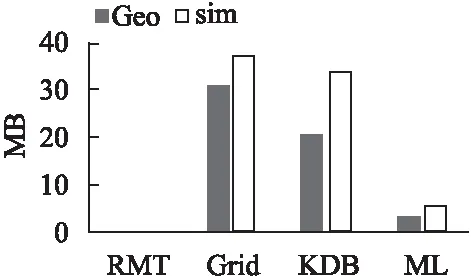
6.1 索引大小对比
6.2 查询性能比较
7 结 论

