学“整式乘法与因式分解”, 从读教材开始
钟鸣
同学们,教材是我们学习的根本。在学习本章之前,先浏览一遍,你会发现,本章由两部分构成——“整式乘法”和“因式分解”,它们是互逆变形。在本章的学习中,我们要学着从两个方向(顺向与逆向)看问题,培养逆向思维。
例如:乘法公式(a+b)(a-b)=a2-b2,顺向看是“整式乘法”,两个一次多项式的积变成了一个二次多项式;逆向看是“因式分解”,一个二次多项式分解成了两个一次多项式的积。
深入阅读各节内容,我们还会发现这样的结构:“用不同的方法从不同的角度计算同一个图形的面积,获得等式”→“利用归纳,合情推理,得出法则或公式”→“依据运算律,通过演绎推理,证实结论”。这是贯串全章的基本方法,也是代数领域非常重要的学习方法。我们完全可以将这一基本方法拓展到对完全立方公式的研究中。
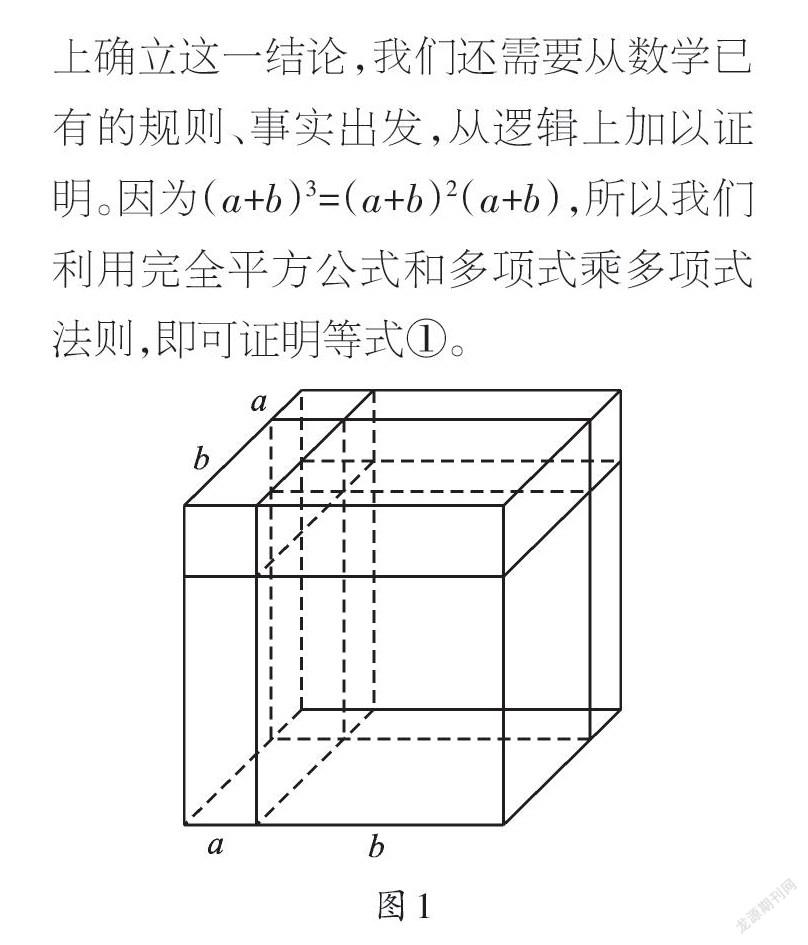
如图1,已知一个边长为a+b的正方体。对于其体积V,我们可以直接整体计算,得到V=(a+b)3;还可以利用两个小立方体的体积与6个小长方体的体积之和计算,即a3+b3+3a2b+3b2a。于是,我们得到等式①(a+b)3=a3+b3+3a2b+3b2a。
上述结论中,a、b的取值局限于正数。为了得到一般的结论,我们不妨假设以下三类情况:1.a、b中有一个是负的;2.a、b都是负的;3.a、b中有一个(或两个)取值为零。我们将这3种情况分别代入等式①的左右两边,通过验证、归纳,猜想等式①对于任意实数都成立。但是,这只是猜想。为了在更一般意义上确立这一结论,我们还需要从数学已有的规则、事实出发,从逻辑上加以证明。因为(a+b)3=(a+b)2(a+b),所以我们利用完全平方公式和多项式乘多项式法则,即可证明等式①。
读完这一章,我们再回头想一想便能感觉:在知识形成的过程中,图形(几何)直觀、符号意识、推理能力是比较重要的。
图形直观指画一个图形,直观表示所思考对象的数学特征(关系),以便分析问题。其指导思想就是数形结合。我们所熟知的表格、线段图、条形图、扇形图以及点和线段的表示等,都是图形直观。在本章中,图形直观体现在画一个图形来表示两个可以画等号的代数式,这既可以解释“整式乘法”,也可以解释“因式分解”。
符号意识就是主动使用符号的意识。我们在数学学习中,接触的数学符号主要有两类:1.数字、字母、图像(表)等对象符号;2.加、减、乘、除、等于、不等于等运算符号。运用符号,我们可以表示数、数量关系和变化规律,还可以进行运算和推理。在本章中,用符号表示规律,发现公式(等式①),就是主动运用符号表示的过程;对所发现的公式,依据运算律和法则进行证明,就是符号操作的过程。
如果想把一般的规律揭示出来,你就不得不进行符号表示;如果想证明规律的正确性,你就不得不进行符号操作。这两个过程既是代数运算的过程,也是初中代数与小学算术的最大不同。
进入初中后,我们更加重视由合情推理和演绎推理构成的完整推理过程。合情推理用于探索思路,发现结论;演绎推理用于证明结论。合情推理和演绎推理是相辅相成的两种推理形式,是学习本章以及全部“数与代数”领域知识的有效工具。我们在阅读教材的同时,要留意去体验、认识、经历这样的推理过程,在进行合情推理时思考“合情”的理由,在进行演绎论证时注重寻找合理的证明思路。
总之,学习数学要阅读教材,要重视知识形成的过程,把握一章的主线,总结基本方法,更要锤炼数学能力,增强数学意识,体悟数学思想,感受数学趣味。
(作者单位:江苏省无锡市西漳中学)
——兼论数学证明中的推理

