关于列车时刻表效用值优化问题的求解研究
沈 洁,祖天琪,宋雨徽,太文芳
(辽宁师范大学 数学学院,辽宁 大连 116029)
0 引言
优化问题是基于现有资源使效益最大或为实现某目标使成本最低的问题[1].本文研究的列车时刻表效用值问题是非光滑优化问题[2],求解方法通常包括最速下降法、黑盒子方法、束方法等[3].最速下降法需要对次微分有整体地全面了解,黑盒子方法无法保证目标函数的下降,二者的不足较明显,而束方法结合了最速下降法的下降性和黑盒子方法的稳定性[3],效果较好.常规的束方法有水平束方法、信赖域束方法、惩罚束方法等[3].在实际运算中,目标函数值往往不能被精确算出,通常得到的是近似值,故近几年有多名学者利用目标函数近似值对束方法展开研究,如:张清叶等[4]提出了一种求解非光滑凸规划问题的混合束方法;董小霞等[5-7]利用目标函数的近似信息研究非精确束方法;沈洁等[8-9]利用惩罚束方法解决通信数据网络优化问题近似模型的相关问题并研究了非光滑无约束凸规划的混合束方法;U.Brannlund等[10]介绍了一种针对列车时刻表优化问题的拉格朗日松弛方法;A.A.Abderrahman等[11]介绍了一种针对列车时刻表优化问题的聚集束方法.列车时刻表效用值优化问题是指寻找一个科学可执行的列车时刻表来使轨道运输产生的效用值达到最大的问题.本文针对列车时刻表效用值优化问题提出了一种改进的束方法,即通过使用指示函数将约束问题转换成无约束问题,利用束方法基本思想构建了切平面近似模型,在此基础上以对偶理论为基础,给出了原规划与对偶规划最优解的显式表达,并得到了近似优化模型的一些相关结论,为后续算法构造奠定了基础,对于轨道交通运营效率的提高具有重要的客观参考价值.
1 预备知识与模型构建
首先给出非光滑优化基本概念、束方法相关理论和列车时刻表优化效用值优化问题的近似模型.
定义1(次微分) 设f(x)是Rn上的凸函数,f(x)在x点处的次微分定义为
∂f(x)={s∈Rn|f(y)≥f(x)+sT(y-x),∀y∈Rn}.
定义2(εk次微分) 设f(x)是Rn上的凸函数,εk>0为常数,f(x)在x点处的εk次微分定义为
∂εkf(x)={s∈Rn|f(y)≥f(x)+sT(y-x)-εk,∀y∈Rn}.
定义3(法锥) 设S⊂Rn非空,集合S在点x∈S处的法锥NS(x)定义为
NS(x)={d∈Rn|dT(y-x)≤0,∀y∈S}.
列车时刻表效用值问题(TTP)是指寻找一个科学可执行的列车时刻表来使轨道运输产生的效用值达到最大的问题.科学可执行意味着既要满足每列列车在特定的时间段内不发生冲突,又不能超出铁路系统的基础设施与轨道容量的限制.优化列车时刻表主要考虑的效用值规划问题是[9]:
(1)
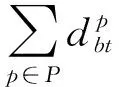
只考虑问题(1)中的第一个约束,引入对偶变量y∈Rn,则问题(1)的拉格朗日函数为
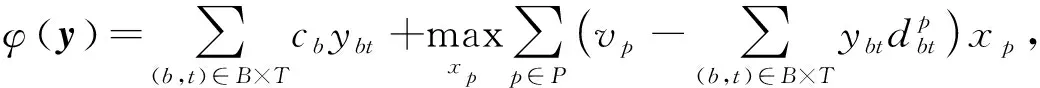
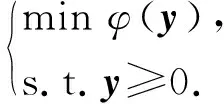
(2)
引入指示函数
其中D={y|y≥0},y≥0表示y的每个坐标都大于或等于零,文中类似情形不再说明.则问题(2)可改写为一个无约束优化问题,具体为
(3)
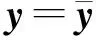
为避免步长较大,问题(3)中增加二次项,引入控制参数uk调整步长,相应效用值子问题为
(4)
定义额定下降为
(5)
2 基于近似模型对偶问题最优解的表达及相关性质研究
定理2.1设yk+1是列车时刻表近似模型子问题(4)的最优解,那么
(6)
证明将问题(4)写成一个带有额外标量r的二次规划问题,具体为
(7)
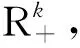
整理后得到
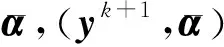
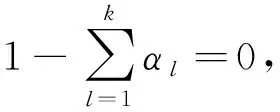
其中
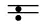

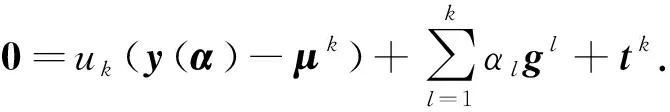
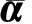
因此
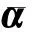
(8)
定理2.2对于时刻列车表效用值优化模型近似问题(4),有以下结论成立:
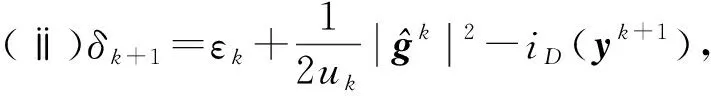
证明(ⅰ) 根据问题(4)的最优性条件和k的定义,有
故
(ⅱ) 由于没有对偶间隙,原规划(4)与对偶规划(8)最优值等价,即
由式(4)和式(5)有
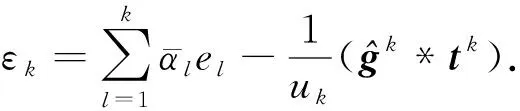
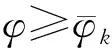
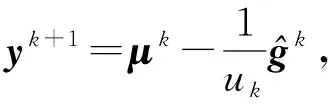
由于μk为稳定中心,yk+1为最优解,则iD(μk)=0,iD(yk+1)=0.应用式(5)额定下降的定义和(ⅱ)的结论,有
因此
φ(y)+iD(y)≥φ(μk)+iD(μk)+k*(y-μk)-εk.
故
k∈∂εkφ(μk)+∂εkiD(μk).
3 结语
本文采用传统惩罚束方法对列车时刻表效用值优化问题展开了研究.通过增加指示函数构建目标函数的近似模型,利用束方法基本思想构建了切平面近似模型,以对偶理论为基础,给出了原规划与对偶规划最优解的显式表达以及近似优化模型的一些相关结论,为后续算法构造奠定了基础.

