基于虚拟线路补偿的主动配电网混合仿真接口实现方法
鄂涛, 尹忠东, 王群飞
(新能源电力系统国家重点实验室(华北电力大学),北京 102206)
0 引言
含有风电、光伏等多种分布式电源的主动配电网已经成为未来智能配电网发展重要的方向[1—3]。新能源的接入使配电网各环节特性及其相互作用机理都发生了深刻变化[4—7],因此,有必要对新能源设备运行特性及其对电网的影响进行研究。传统的数字仿真难以精确模拟分布式电源的动态特性[8],而物理模拟仿真造价高、灵活性差,难以对主动配电网的多种工况进行模拟[9]。数字物理混合仿真将两者优势相结合,将大规模的电力网络运行于实时仿真器中,而需要准确模拟的分布式电源物理设备则通过功率接口接入[10—13],这种方式又称为功率硬件在环(power-hardware-in-the-loop,PHIL)仿真,是未来主动配电网仿真分析的重要手段[14—15]。
连接数字侧与物理侧的功率接口是PHIL系统中的关键环节。受延迟、噪声等原因影响,功率接口中引入的误差会影响仿真系统的精度与稳定性[16—17]。针对不同的仿真对象,应选用合适的接口算法,目前最为常用的有理想变压器模型(ideal transformer model,ITM)法和阻尼阻抗法(damping impedance method,DIM)2种[18]。在应用于主动配电网混合仿真时,这2种方法主要存在如下问题:(1) ITM法实现简单,但稳定性较差[19],一旦发生失稳,会损坏物理设备,且接口延时会对ITM的精确性产生影响;(2) DIM的关键在于阻尼阻抗与物理侧阻抗的实时匹配[20],但主动配电网系统物理侧的阻抗难以实时测量与跟踪。
针对以上问题,文献[21]在ITM法的基础上,选择在物理侧串入电抗器,以解决稳定性问题,但该方法在增加成本的同时会降低仿真精度。文献[22—23]加入了虚拟电阻和虚拟阻抗对ITM的反馈电流进行补偿。该方法需要提前对阻抗取值进行设计,以保证接口性能,但主动配电网运行工况复杂难以预测,阻抗取值计算十分困难,故无法直接应用于主动配电网的混合仿真中。文献[24—25]基于DIM,通过采集物理侧电压和电流实时计算等效阻抗,但该方法无法应用于主动配电网这类有源系统。文献[26]将简化后的DIM与ITM法相结合得到了一种改进接口算法,但该方法需要在仿真器中建立2套相同的仿真模型,而主动配电网仿真系统规模较大,现有仿真器的运算速度难以满足该需求。
由上述分析可知,现有的功率接口算法均无法迎合主动配电网混合仿真的需求。因此,文中提出一种基于虚拟线路补偿的改进ITM法,在ITM法的基础上,在数字侧与物理侧间增设了一条虚拟线路。在线路上的虚拟电流对系统进行稳定性补偿的同时,根据虚拟功率对接口两侧的相位差进行补偿。该方法消除了接口延迟及稳定性补偿所引入的误差,简化了接口参数选取过程,既保证了系统稳定性又提升了仿真精度。与现有方法相比,该方法能适应物理侧有源、非线性等多种情况,且不必额外增加物理设备,实现简单。仿真和实验结果表明,所提方法在主动配电网混合仿真的不同工况下效果均良好。
1 PHIL系统结构及稳定性分析
1.1 配电网混合仿真系统结构
主动配电网PHIL仿真系统主要由数字仿真系统(digital simulation system,DSS)、物理仿真系统(physical simulation system,PSS)及功率接口三部分组成,PHIL仿真系统具体结构如图1所示。

图1 PHIL仿真系统结构Fig.1 Structure of PHIL simulation system
DSS是运行于实时仿真器上的主动配电网数字模型,PSS是模拟线路、可编程负载、风电光伏模拟器、无功补偿装置等的物理模拟装置,两者通过功率接口相连进行数字物理混合仿真。DSS中电压、电流数字信号经D/A转换器转换为模拟信号后,经四象限功放放大为功率流,并作为激励送入PSS侧。电压/电流互感器采集到实际物理设备的电压和电流模拟信号后,经A/D转换器反馈回DSS侧,用于求解下一仿真步长的系统状态。
功率接口部分中硬件装置存在不可避免的传输延时,数模转换装置和互感器的延迟一般很小,可以忽略,但功放的延时较大,会对系统的稳定性及仿真精度产生影响。文中以ITM法为例对PHIL仿真系统的稳定性进行分析。
1.2 ITM稳定性分析
ITM法是最基本、实现最为简单的一种接口算法,分为电压型和电流型2种。电压型ITM接口结构如图2所示,基于替代定理将物理侧在数字侧等效为受控电流源,通过互感器采集功放输出的电流i2进行控制;数字侧电压U1作为功放的控制信号,功放等效为受控电压源,在物理侧施加电压U2。i1为受控电流源所在支路的电流;Td为功放的传输延时;Z1,Z2分别为数字侧和物理侧的等效阻抗;US,UH分别为数字侧和物理侧的等效电源。

图2 电压型ITM接口结构Fig.2 Interface structure of voltage type ITM
由于延时的存在,在同一时刻U1和U2间存在误差量ε,电压误差会在物理侧形成电流误差Δi。
Δi=ε/Z2
(1)
误差Δi传回数字侧,进一步导致数字侧出现电压误差ΔU。
ΔU=-(Z1/Z2)ε
(2)
当|Z1/Z2|>1时,误差量将在循环过程中不断放大,最终导致系统失去稳定。ITM的开环传递函数为:
GITM=(Z1/Z2)e-sTd
(3)
根据奈奎斯特稳定性判据也可以获得ITM稳定的充要条件为|Z1/Z2|<1,即数字侧阻抗小于物理侧。但对主动配电网混合仿真而言,数字侧一般为含有分布式电源的复杂配电网数字仿真模型;物理侧为分布式电源、多条模拟线路及多个负载。物理侧接入位置的选择、分布式电源及负荷的投切、故障的发生,均会使数字侧和物理侧等效阻抗比值发生变化。当两者之间关系不再满足稳定条件时,系统会失稳,因此需要在ITM法的基础上针对稳定性及延迟问题进行改进。
2 基于虚拟线路补偿的改进ITM法
假设在数字侧和物理侧之间存在一条如图3所示的虚拟线路,线路的首末端电压分别等于U1和U2;线路阻抗为Z*;虚拟线路的压降即为误差量ε。由于两端电压差的存在,线路上会产生虚拟电流I*和虚拟功率S*。I1为受控电流源输出电流;I′1为流过数字侧阻抗的电流;I2为受控电压源输出电流;I′2为流过物理侧阻抗的电流;T为系统的总传输延迟。

图3 基于虚拟线路补偿的接口结构Fig.3 Interface structure based on virtual line compensation
文中所提的基于虚拟线路补偿的改进ITM法包含接口稳定性改进和精确性补偿两部分。精确性改进策略能消除系统固有延迟和稳定性补偿引入系统的误差,保证了接口的精确性。而当系统状态发生突变后,精确性补偿策略在短时间内无法实现对相位的完全补偿,系统可能发生失稳。此时,便需要通过稳定性改进算法使系统在仿真过程中一直保持稳定。改进算法的两部分相辅相成,共同保证了接口的精度与稳定性。
2.1 稳定性改进
由ITM稳定的充要条件可知减小数字侧等效阻抗或增大物理侧等效阻抗均可达到增强稳定性的目的。在频域内对系统稳定性进行分析,虚拟线路的引入会产生虚拟电流I*,此时I1,I′1,I2,I′2具体数量关系变为:
(4)
受控电流源的控制量由I2变为:
I1=I′2=I2+I*
(5)
其中:
I*=(U1-U2)/Z*
(6)
由图3可得,含虚拟线路功率接口的交互方程为:
(7)
当UH=0时,可得:
(8)
联立式(4)—式(8),可得:
(9)
引入虚拟线路后,接口开环传递函数为:
(10)
由奈奎斯特稳定性判据可知,引入虚拟线路后,接口稳定条件为:
(11)
加入虚拟线路后,系统的稳定性不光取决于Z1和Z2的比值,Z*的取值变化同样会影响系统稳定性。令s=jω,则数字侧、物理侧及虚拟线路阻抗值分别为:
(12)
式中:R1,L1分别为数字侧的等效电阻与电感;R2,L2分别为物理侧的等效电阻与电感;R*,L*分别为虚拟线路阻抗的电阻与电感;且有X1=ωL1,X2=ωL2,X*=ωL*。将式(12)代入式(11)中,化简后稳定条件变为:
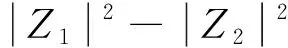
(13)
令:
(14)
将式(14)代入式(13)中,根据数字侧阻抗Z1和物理侧阻抗Z2的大小关系不同,稳定条件可转化为以下3种情况。
(1) 当|Z1|>|Z2|时,稳定条件为:
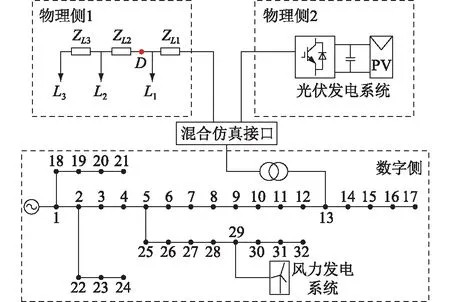
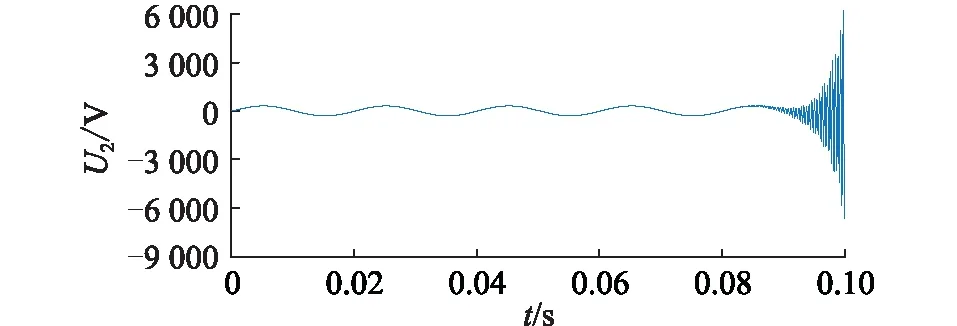
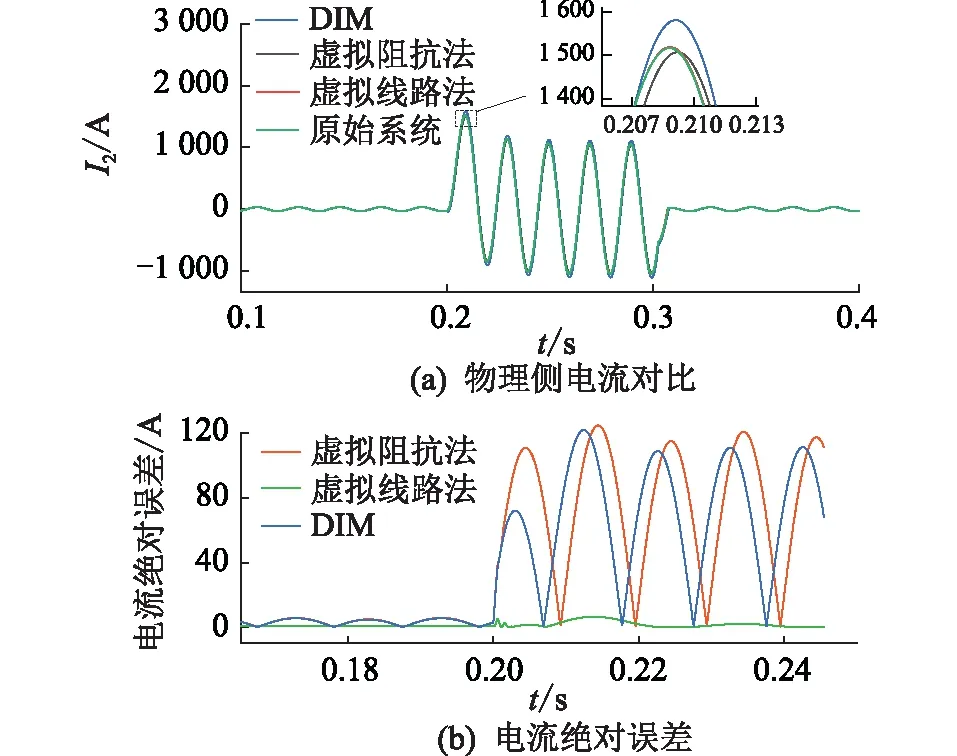
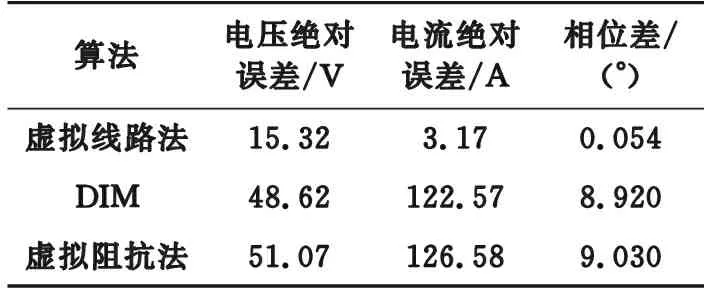
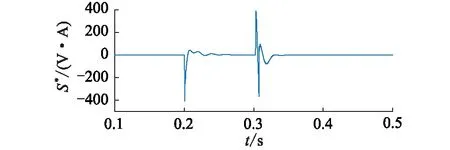
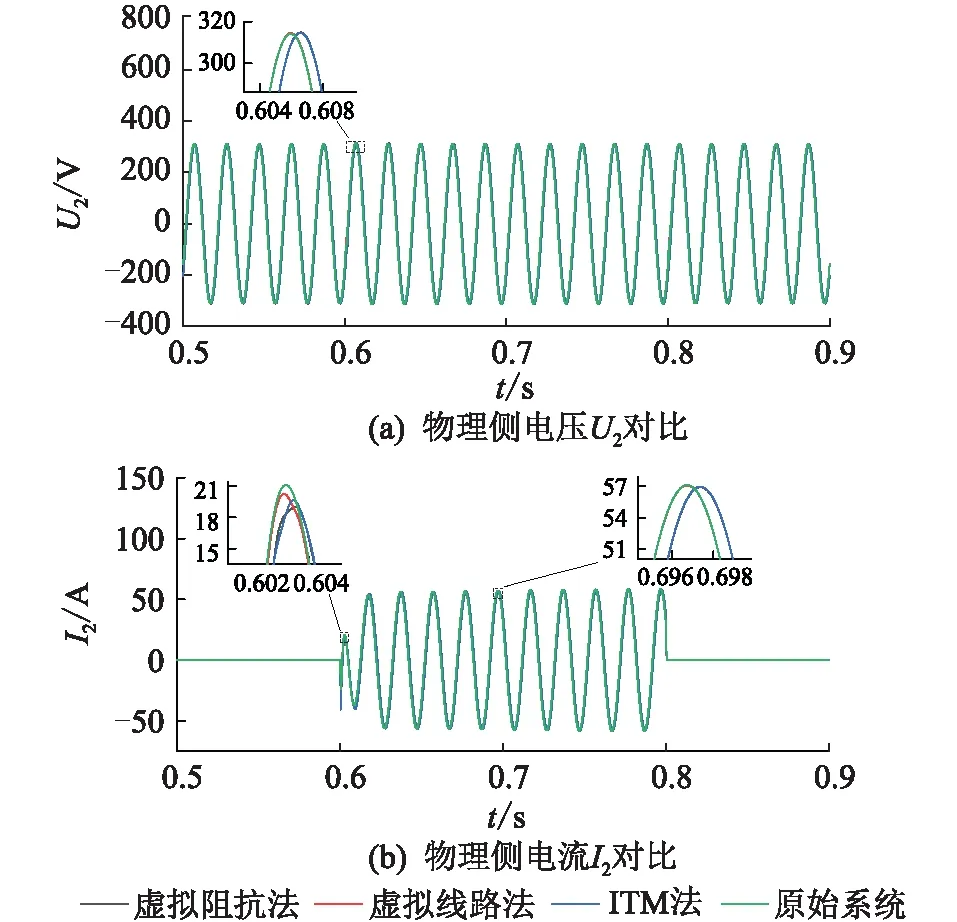
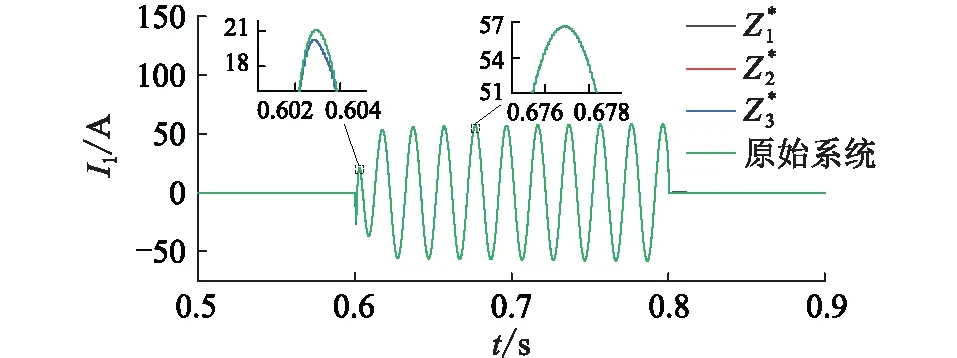
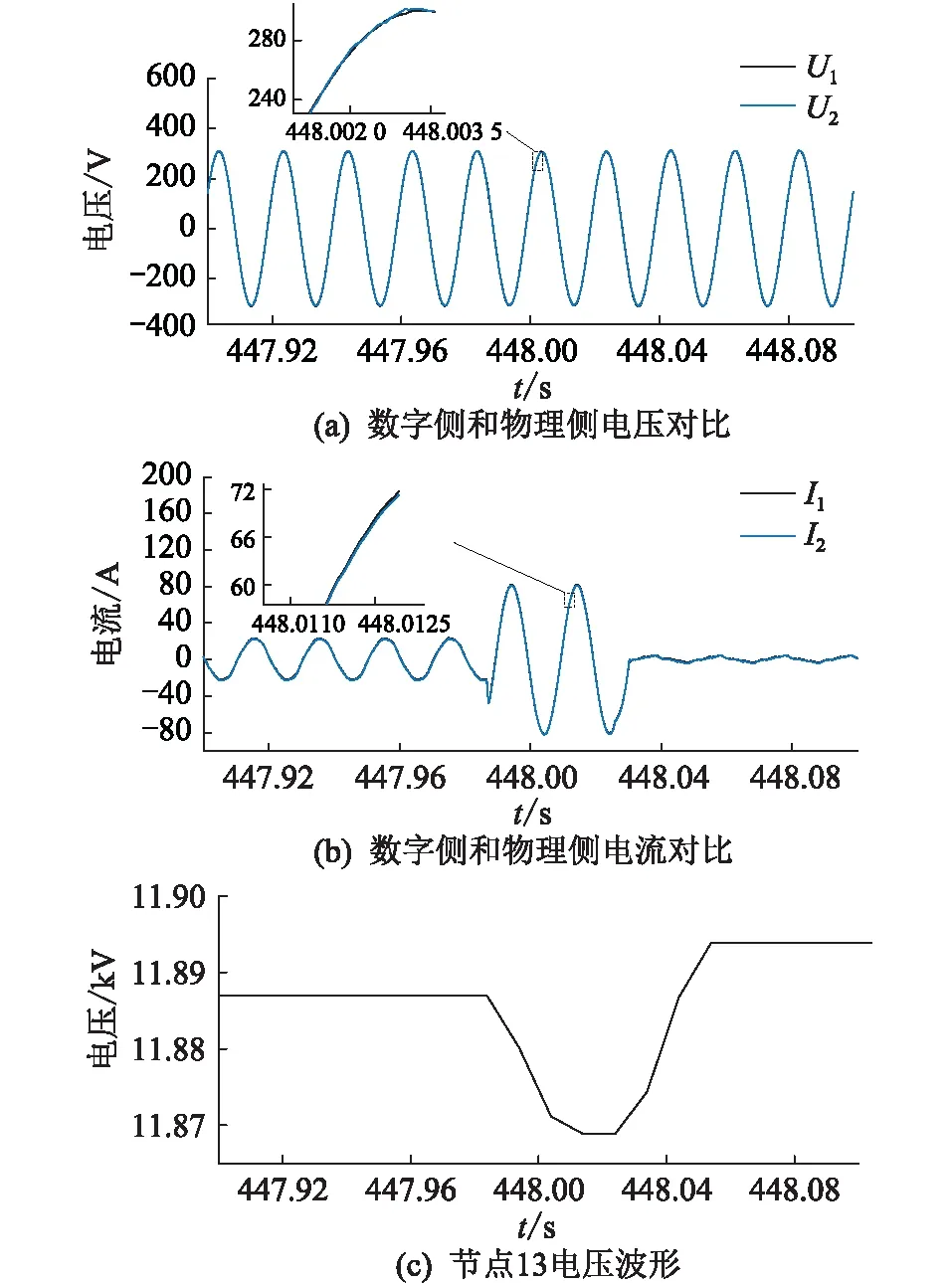
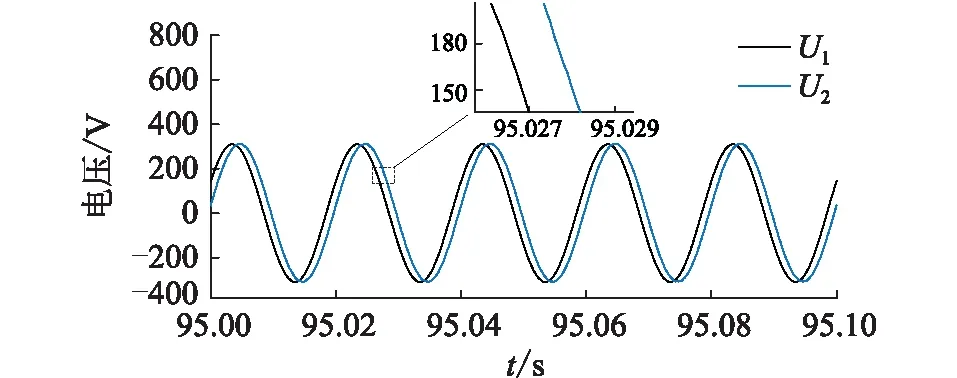
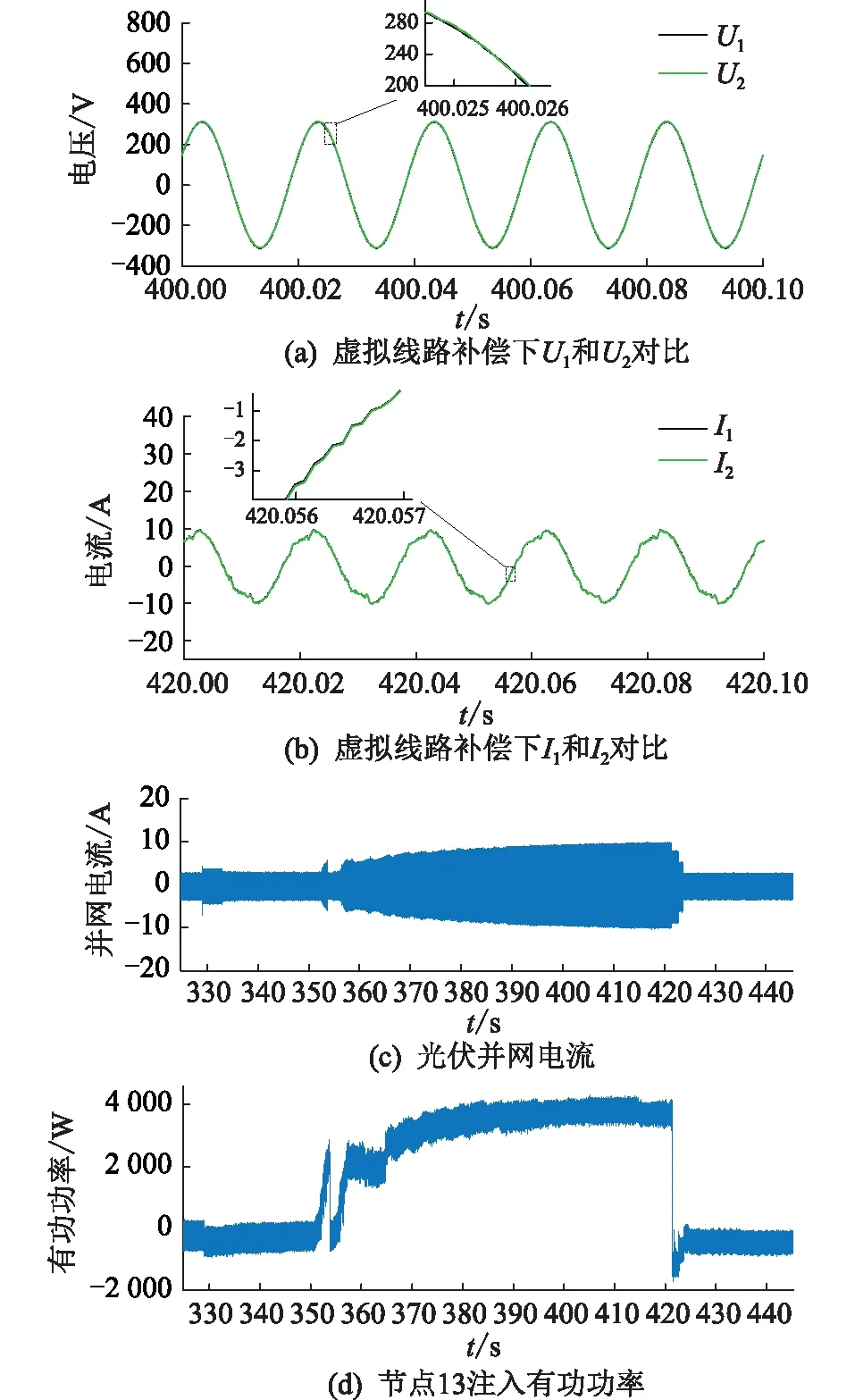
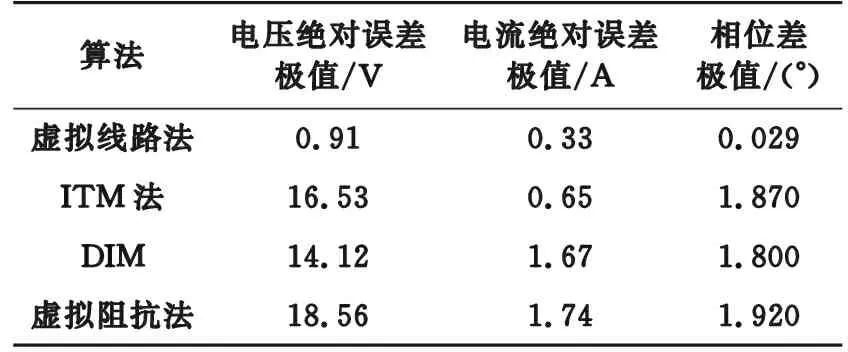
(R*-a)2+(X*-b)2 (15) (2) 当|Z1|<|Z2|时,稳定条件为: (R*+a)2+(X*+b)2>a2+b2 (16) (3) 当|Z1|=|Z2|时,若满足R*>0,X*>0,式(13)恒成立。 虚拟线路阻抗取值范围示意见图4。当|Z1|>|Z2|时,虚拟阻抗取值在圆O1内稳定;当|Z1|<|Z2|时,虚拟阻抗取值在圆O2外的区域稳定;当|Z1|=|Z2|时,虚拟阻抗取值在第一象限内稳定。所以只要虚拟线路阻抗值在3种情况取值范围的交集内,即图中的深色区域内时,混合仿真系统就可以一直保持稳定。 图4 虚拟线路阻抗取值范围Fig.4 Value range of virtual line impedance 虚拟线路的引入在改变系统稳定性的同时,也会影响系统的仿真精度。在理想状态下,数字侧受控电流源输出电流I1和物理侧实际电流I2应相等,但观察式(5)、式(6)可以发现,虚拟阻抗Z*的引入会使两者之间产生偏差,虚拟阻抗的模越小,偏差越大。为尽量减小误差,应将虚拟阻抗设置为稳定范围内的最大值。但在进行主动配电网混合仿真时,往往需要在多种工况间进行切换。为保证系统在切换前后及过程中一直保持稳定,接口需要拥有较大的稳定裕度,因此虚拟线路阻抗的取值Z*应满足: (17) 功放的延时会导致同一时刻的U1和U2不再相同,在频域表现为交流信号的相位滞后,因此对延迟产生的电压相位差进行补偿可起到减小误差量ε,增强系统稳定性和精确性的效果。主动配电网混合仿真的实际过程中,由于分布式电源、噪声干扰等原因,电压信号中会含有一定量的谐波,加大了获得准确相位差的难度。通过傅里叶分解,对各次谐波相位分别进行计算是获取精确相位差最为常用的方法。但此方法计算复杂,耗时长,无法满足实时补偿的要求[27—28],因此文中提出了基于虚拟线路的相位补偿策略。当延时存在时,由于线路两端电压相位差,线路上会产生虚拟功率S*。 (18) 当相位差被完全消除时,S*= 0。虚拟功率的变化只受两端电压相位差Δθ影响,因此可以通过跟踪线路上虚拟功率的变化得到需要补偿的相位大小。基于虚拟线路上功率的延时补偿原理见图5,ωt为初始相位,通过数字系统仿真的同步时钟获得;U′abc为重构后三相电压信号。。 图5 基于虚拟线路的相位补偿原理Fig.5 Principle of phase compensation based on virtual line 通过式(18)计算获得虚拟功率S*后,将其作为误差信号送入比例积分(proportional-integral,PI)调节器,调节器输出需要补偿的相位补偿信号Δθ。对虚拟线路首端电压U1进行Park变换,变换得到dq坐标系下的直流量Ud,Uq,U0。 (19) 式中:P1为变换矩阵;Ua,Ub,Uc分别为U1的三相电压分量。 (20) 将初始相位与补偿信号相加后,逆变换矩阵P2变为: (21) 再对Ud,Uq,U0进行Park逆变换,经过相位补偿后即可重新生成电压信号U′a,U′b,U′c。 (22) 将经过逆变换后的电压信号作为功放的输入信号,物理侧即可获得一个相位相同的信号。当相位被完全补偿时,虚拟阻抗的取值对系统仿真精度的影响被完全消除。此时,Z*可以在图4深色区域内任意取值,不同取值对仿真精度影响极小。相位补偿的加入使虚拟阻抗值取值变得相对自由,系统在获得较高稳定裕度的同时,精确性也获得了保证。 为验证基于虚拟线路补偿的改进ITM法应用于主动配电网混合仿真系统的有效性,及相对于现有算法在稳定性和精确性上的提升,在Simulink中搭建了如图6所示的主动配电网数字物理混合仿真系统模型。 图6 主动配电网混合仿真结构Fig.6 Hybrid simulation architecture for active distribution network 数字侧为IEEE 33节点标准配电网,在配电网的节点22接有永磁同步机风力发电系统;物理侧通过功率接口接入配电网节点13,物理侧分为无源的配电网馈线和光伏发电系统2种情况。仿真步长为10 μs;功放的延时设置为500 μs。 为模拟实际情况,物理侧线路阻抗参数采用实验室现有的10 kV模拟线路实际参数,具体数值为: (23) 负荷L1,L2,L3的有功功率均设置为3 kW,设置无功功率为3 kvar;线路电压等级为800 V,通过变压器接入数字侧配电网13节点。图7为ITM法下物理侧电压U2的仿真波形。 图7 ITM法下物理侧电压Fig.7 Physical side voltage in ITM method 由图7可知,在功率接口采用ITM法时,由于数字侧阻抗大于物理侧,不满足ITM稳定的条件,仿真系统在约0.08 s后失去稳定。 虚拟线路阻抗中设定R*=1 Ω,L*=0.01 H。0.2 s时在D点设置三相直接接地短路故障,0.3 s时故障切除。分别将DIM、虚拟阻抗法、虚拟线路法与未添加功率接口的原始系统相对比。其中虚拟线路法为文中所提的基于虚拟线路补偿的改进ITM法;虚拟阻抗法为仅加入相同虚拟阻抗值的稳定性补偿,未使用精确性补偿的情况。以原始系统为标准,结合式(24),将绝对误差作为衡量精确性的指标,对接口处电压电流进行分析。 Δx=|x-xorig| (24) 式中:x为需要进行对比的变量;xorig为变量在原始系统中的值。不同算法间物理侧输出的仿真电压U2波形及故障前后绝对误差分析结果如图8所示,输出电流I2波形及故障前后绝对误差分析结果如图9所示。 图8 故障前后不同接口算法电压对比Fig.8 Voltage comparison of different interface algorithms before and after fault 图9 故障前后不同接口算法电流对比Fig.9 Current comparison of different interface algorithms before and after fault 相对于原始系统,不同算法的接口电压、电流绝对误差及电压相位差对比结果如表1所示,其中绝对误差均取仿真过程中的最大值。 表1 不同算法性能对比Table 1 Performance comparison ofdifferent algorithms 由图8和图9可知,当接口为只采用稳定性补偿的虚拟阻抗法时,系统在故障前后可以一直保持稳定,说明了利用虚拟线路上流过的电流对数字侧受控电流源控制信号进行补偿,可有效提升仿真系统的稳定性。再结合表1分析可以发现,由于相位差的存在,只采用稳定性补偿时,接口处电压、电流存在较大的误差,并且稳定性补偿的加入会使电流误差进一步扩大。在根据虚拟线路上流过的虚拟功率对接口两侧的相位差进行补偿后,输出电压、电流波形与原始系统几乎重合,误差相对于其他2种算法显著降低,说明精确性补偿环节成功消除了稳定性补偿及固有延迟所引入的误差,大幅提升了仿真精度。虚拟线路上虚拟功率的流动情况如图10所示。 图10 线路虚拟功率Fig.10 Line virtual power 可以发现当系统处于稳态时,虚拟功率趋近于0。系统状态发生突变时,线路上产生大小为400 V·A的虚拟功率,在相位补偿环节的作用下经短暂的振荡后迅速衰减为0,证明虚拟线路法能高效补偿相位差,且具有良好的鲁棒性。 光伏发电系统的额定功率为30 kW,设置光伏发电系统0.2 s时并入配电网,0.4 s时离网。虚拟线路阻抗设定R*=10 μs,L*=0.05 H,分别将ITM法、虚拟阻抗法、虚拟线路法与原始系统作对比。不同算法间物理侧输出的仿真电压U2波形如图11(a)所示,电流I2波形如图11(b)所示。 图11 不同接口算法物理侧仿真波形对比Fig.11 Comparison of simulation waveforms on physical side of different interface algorithms 观察图11(a)可知,在光伏发电系统并网的暂态过程及并网后的稳态过程中,虚拟线路法的物理侧电压和原始系统的完全重合,而虚拟阻抗法和ITM法受到功放延迟的影响,电压均出现了相位的滞后与数值上的偏差。观察图11(b)可知,光伏并网的暂态过程中,虚拟线路法的电流在开始阶段与原始系统存在偏差,偏差随时间减小,并在4个周期后完全消除;而虚拟阻抗法和ITM法在暂态和稳态过程中均与原始系统存在较大偏差。在离网过程中,虚拟线路法的精确性也远高于其他2种算法。说明虚拟线路法在物理侧有源且含有非线性元件的情况下,依然具有良好的补偿效果。 图12为采用虚拟线路法时,3种不同阻抗取值下受控电流源控制信号I1与原始系统的对比,其中: (25) 图12 不同虚拟阻抗电流对比Fig.12 Comparison of different virtual impedance currents 从图12中可以看出,当线路阻抗在稳定范围内取不同数值时,电流波形几乎没有变化。经计算,仿真过程中,不同阻抗取值下,电流绝对误差均保持在1.6 A以内,且相差不大。说明虚拟线路阻抗对仿真精度的影响被精确性补偿环节消除,线路阻抗的参数可在稳定范围内任意取值,不必再针对不同场景进行参数优化,大幅简化了接口参数选取过程。 实验数字部分采用IEEE 33节点标准配电网,物理仿真子系统为800 V模拟10 kV电压等级的3条电缆线路,线路阻抗如式(23)所示,线路上带有3个可编程负载,有功功率均设置为3 kW,无功功率均设置为3 kvar。每条线路上都设有过流保护,在图6中的D点设有故障模拟器,可以实现物理侧多种故障模拟,物理侧通过功放接入物理侧节点13。在D点设置三相短路故障,短路电阻设置为20 Ω。故障过程数字侧电压U1和功放实际输出电压U2对比如图13(a)所示,数字侧等效电流I1及功放实际输出电流I2波形对比如图13(b)所示,节点13的电压波形如图13(c)所示。 图13 物理侧三相短路故障实验Fig.13 Experiment of three-phase short circuit fault on physical side 由图13可知,在物理侧发生三相短路故障后,数字侧及物理侧电流升高,电压降低,节点13电压降低。过流保护动作后,负荷L2,L3及其所在线路被迅速切除,数字侧及物理侧电流比故障前有所减小,节点13电压升高。观察图13(a)和图13(b)可发现,当采用虚拟线路法时,系统可以一直保持稳定,物理侧和数字侧的电压电流波形保持一致。 为量化对比分析,文中对ITM法[19]、DIM[20]及虚拟阻抗法[23]也进行了实验。以实验过程中接口两侧电压、电流绝对误差极值、数字侧与物理侧电压相位差极值作为评价指标,与文中所提的虚拟线路法进行对比,对比结果如表2所示。 表2 故障实验时不同算法性能比较Table 2 Performance comparison of different algorithms during failure experiments 由表2可知,文中方法相对于ITM法具有更强的稳定性,且精确性大幅优于DIM和虚拟阻抗法。虚拟线路法有效降低了电压、电流绝对误差,使用的相位补偿方法能高效补偿延时所引入的相位差,解决了虚拟阻抗引入带来的精确性问题。 实验数字部分采用IEEE 33节点标准配电网,物理仿真子系统为380 V的光伏发电系统,最大输出功率设置为4 kW。选用ITM法和虚拟线路法2种接口算法进行实验。图14为光伏并网、离网过程中数字侧电压U1和功放实际输出电压U2的对比。 图14 ITM法下数字侧和物理侧电压对比Fig.14 Voltage comparison between digital side and physical side in ITM method 由图14可以看出,使用ITM法时,在接口处电压存在100 μs左右的延迟,混合仿真系统存在较大误差。选用虚拟线路法的光伏并网过程中,数字侧电压U1和功放实际输出电压U2波形对比见图15(a),数字侧等效电流I1及功放实际输出电流I2波形对比见图15(b),功放输出电流波形见图15(c),注入配电网的有功功率见图15(d),。 图15 光伏并、离网实验Fig.15 Photovoltaic grid-connected and off-grid experiments 对比图14和图15(a)可发现,使用了虚拟线路法后,功放及信号传输过程中产生的相位差被有效消除。文中方法与已有算法的实验数据量化分析对比结果如表3所示。 观察表3可以发现,虽然4种接口算法在实验过程中均能保持稳定,但ITM法、DIM、虚拟阻抗法的误差较大,物理侧与数字侧存在明显的相位差,仿真精度低。虚拟线路法的3项指标均明显优于其他3种算法,精确性更高。由表3、图15(a)和图15(b)可知,虚拟线路法的精度能满足主动配电网混合仿真要求,实现了数字侧和物理侧同步运行,仿真接口“透明”。观察图15(c)和图15(d)可知,采用了虚拟线路法的主动配电网数字物理混合仿真系统,可以将分布式电源真实的动态响应反映到电网中,为今后相关研究打下了良好的基础。 表3 光伏并、离网实验不同算法性能比较Table 3 Comparison of the performance of different algorithms in photovoltaic grid-connected and off-grid experiments 文中提出了一种基于虚拟线路补偿的数模混合仿真接口算法,并以主动配电网混合仿真为应用场景对该方法进行了理论分析、仿真计算及实验验证,得到了如下结论: (1) 当虚拟线路阻抗取值在稳定范围内时,虚拟线路的加入能提升混合仿真系统的稳定性。但只采用稳定性补偿时,虚拟阻抗的加入会降低系统的仿真精度。 (2) 精确性补偿策略在保证稳定性的同时,可以弥补稳定性补偿在精确度方面的缺陷。通过相位补偿,能使线路阻抗的取值变得相对自由。 (3) 在主动配电网故障,光伏并、离网混合仿真时,虚拟线路法相对于其他算法具有更高的稳定性和精度性。且所提方法实现简单,在实际硬件在环实验中能达到良好的效果。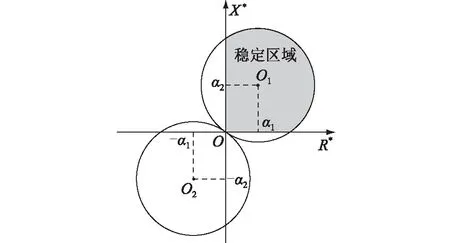
2.2 精确性补偿
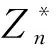

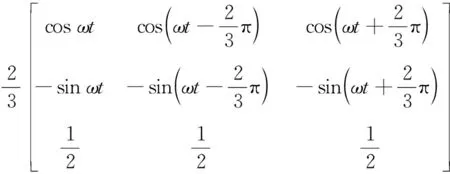

3 接口稳定性及精确性仿真分析
3.1 主动配电网稳态及暂态仿真

3.2 光伏并、离网过程仿真
4 实验验证
4.1 物理馈线故障实验

4.2 光伏并、离网实验
5 结论

