基于自适应NSGA-Ⅱ算法的配电网多故障抢修优化决策

陈楚昭， 孙云莲

(武汉大学电气与自动化学院，湖北 武汉 430072)

0 引言

当配电系统由于自然因素或者人为因素发生停电事故时，各级对应的抢修部门应当快速反应，及时组织人员以及物资前往故障点进行抢修工作[1]。但是，当自然灾害或者某些人为因素引发的区域性多故障点、大面积的停电事件发生时，依据人工经验分派抢修任务的方式很难真正合理有效地在最短的时间、尽可能小的停电影响范围内完成抢修任务。

目前，对配电网故障抢修的研究主要集中在对抢修路径优化，抢修任务分配和优化算法的改进，以及对模型和目标等的改进[2—3]。文献[4]提出通过遗传算法寻优和拓扑分析算法判断故障失电区域相关信息，综合迭代得到最佳抢修方案，但仅考虑了单抢修小队的情况而未考虑多小队同时抢修的情况。文献[5]利用电网应急指挥系统的信息，以增强电网运行稳定的裕度和减少停电损失为目标，考虑资源保障率，建立对电网应急抢修资源的调度方案。文献[6]将故障抢修与故障恢复相结合，考虑了多抢修小队协同抢修的工作模式，采用改进的多目标细菌群体趋药性(bacterial colony che￣mo￣taxis,BCC)算法研究计算应急抢修策略。文献[7]考虑到抢修小队不能满足每个故障点对抢修资源的需求，提出将适应度作为外化指标，根据各抢修小队与各故障点之间的匹配程度进行最优任务分配。文献[8]考虑了抢修小队初始位置不同和协作效用，以轮盘赌的选择方式得到抢修方案集合，并采用改进的BBC算法，得出最佳方案和抢修顺序。文献[9]提出了多故障同时出现的应急情况下，单个资源中心无法满足当前资源需求的问题，并以最短的维修启动时间和最少的资源中心为目标建立多资源、多中心调度模型，得到最优的资源调度方案。

文中在配电网多故障抢修过程中考虑了任务分配和各队协同抢修等问题，建立了故障抢修的多目标数学模型。在多目标的处理方法上，考虑到不同地区的配电系统对各个目标的重要性存在差异，因此不预先设置各目标的权重，而是采用非劣解生成法得到Pareto集，避免因权重设置不合适而错过最优策略。算法上采用自适应参数的非支配排序遗传算法(non dominated sorting genetic algorithm,NSGA)-Ⅱ进行求解，同时为了方便决策者从一系列方案中选出最优方案，文中设计了基于角度选择的拐点决策算法，使得多目标优化算法能够直接输出一个比较优秀的解。

1 配电网多故障抢修模型

1.1 配电网多故障抢修问题描述

配电网多故障抢修是一个以各班组的故障任务分配和故障抢修顺序为决策变量的多目标、多约束的非线性混合整数优化问题[10]。配电网多故障抢修问题描述如下：某地区有1个抢修中心，抢修中心有M个抢修班组(s1,s2,…,sM)，抢修中心负责的区域内有N个故障点(r1,r2,…,rN)。设Cm为带有抢修顺序的抢修班组sm所需要抢修的故障点集合，该抢修班组需要从抢修中心出发，顺次经过集合中的所有故障点进行抢修工作，最后返回抢修中心。如Cm={Cm1,Cm2,…,Cmh}，则抢修班组sm须按照o→Cm1→Cm2→…→Cmh→o的顺序进行抢修工作，其中，起点和终点o为抢修中心。每个故障点的抢修任务都可以任意分配给1个抢修班组，每个班组在任务分配后都可以任意安排完成抢修任务的顺序。

由于需要抢修的故障点较多，能够派遣的抢修班组数量有限，因此，须依靠构建的模型合理安排每个抢修班组对应的任务以及抢修的先后顺序，以提升配电网抢修效率，提高供电可靠性。实际抢修中，常对不同的目标进行优化，如最大完工时间、抢修成本、停电损失等，这些目标需要同时进行优化处理，而这些目标又往往是互相冲突的。在各种约束条件下，如何对多目标同时实现优化，合理安排任务分配和完成顺序，就是配电网多故障抢修需要解决的问题[11—13]。

1.2 目标函数的确定

根据上述分析，指定最终的优化目标为完成所有任务所需要的时间最短和故障引发的社会经济损失最小。

目标函数f1(X)为完成所有抢修任务需要的时间最短：

f1(X)=min{maxTm}m=1,2,…,M

(1)

式中：Tm为抢修班组sm完成故障抢修任务所需要的时间，是抢修班组完成任务在路上耗费的时间Tml与各故障点预估的抢修时间Tmy之和。

Tm=Tml+Tmy

(2)

目标函数f2(X)为故障引发的社会经济损失最小：

(3)

式中：K为受故障影响发生停电的负荷数量；bk为负荷k的停电时间；Lk为负荷k的功率；wk为负荷k的重要性权重系数。根据电力负荷的用电设施安全性及整体的供电可依赖性对负荷的重要性作出具体评估，根据其紧要程度分别为一、二、三级负荷，分别设置其权重为w1，w2，w3，则wk可表示为：

(4)

1.3 约束条件的确定

(1) 抢修任务约束。VMN为一个M×N的矩阵，vmn为矩阵中第m行第n列的元素，表示第m个抢修班组是否负责抢修第n个故障点。第m个班组被分配到抢修第n个故障点时，vmn的值为1，其他情况为0，即：

(5)

为满足每个故障点的抢修任务只分配给一个班组，将约束条件定为：

(6)

(2) 抢修时间约束。每个班组的抢修时间应当在合理范围内：

Tm≤TSmm=1,2,…,M

(7)

式中：TSm为班组最大允许抢修时间。

(3) 故障时间约束。每个故障点的修复时间应当在合理范围内：

tn≤tSnn=1,2,…,N

(8)

式中：tn为故障点rn从故障开始到完成修复的时间；tSn为系统规定的最大允许停电时间。

(4) 抢修资源及其他约束。抢修班组提供的抢修资源应当能够覆盖故障点的抢修资源需求，且满足抢修对时间、天气、路况等自然条件的要求。

1.4 模型假设

假设一：每个抢修班组都具备独立处理各类配电网中电力故障的能力，不需要别的抢修班组进行协助；

假设二：每个抢修班组的抢修效率相同，即处理相同故障所耗费的时间相同，且每个抢修班组在同一时间只能处理一个故障任务；

假设三：所有班组拥有的抢修物资相同，并假设抢修物资多数为耐用物资，而易损耗的抢修物资数量足够支持抢修班组不回调度中心连续抢修多处故障点；

假设四：多故障同时发生的情况下，在进行派单调度抢修班组之前，所有故障的地址、故障类型、所需抢修物资都是已知的；

假设五：故障点之间的距离以及故障点和供电所调度距离都按最短直线距离计算，且路上行驶的时间只与距离成正比，没有方向性；

假设六：各故障点的位置、故障原因及故障抢修预估时间都可以在抢修调度前估算得到。

2 基于角度选择的自适应参数NSGA-Ⅱ算法

2.1 NSGA-Ⅱ算法

进化计算是模拟自然界物种演化过程的优化方法，遵循适者生存的规则，目前已被大量应用到各类优化问题中。由于其并行计算的特点，多目标优化算法一般都是基于进化计算设计的。常用的优化算法有多目标遗传算法(multi objective genetic algorithm,MOGA)、小生境Pareto遗传算法(niche Pareto genetic algorithm,NPGA)和NSGA等。其中，NSGA基于Pareto最优的思想来解决多目标优化问题，已有学者引入精英策略和拥挤度计算对NSGA进行了改进，形成了NSGA-Ⅱ算法[14]。

NSGA-Ⅱ算法提出了快速非支配排序策略，简化了运算的复杂程度，并加入了精英策略和拥挤度的比较因子，保证了种群的优良性和多样性，适用于求解多目标优化问题。

2.2 基于角度选择的拐点决策算法

求解优化问题都是为了得出问题的最终方案。利用NSGA-Ⅱ算法往往可以得到多个可行方案，对于多目标优化问题而言，为了得出最终的解决方案，决策者可以根据自己的偏好以及不同目标的重要性做出选择。但研究发现，拐点在多目标优化问题求解得到的Pareto前沿中具有独特的意义[15]，通常被描述为各个区域内的最优解决方案，其主要特点是：从几何角度看，如果Pareto前沿的形状是弯曲的，那么拐点解决方案代表的是那些可以改善整体性能同时又在某些标准上作出微不足道的牺牲的方案[16]。换言之，拐点解决方案可以在某些目标上表现出显著的改进，而在其他目标上却没有明显的降低[17]。拐点的选择策略中比较有代表性的是基于角度的选择[18]，在只有2个目标的情况下，穿过每一个解及其2个邻域解的2条直线之间所形成的角可以作为解是否处于拐点的一个衡量指标，如图1所示。由图1可知，2条线之间的角度α越大，则该方案越趋向于拐点[19]。

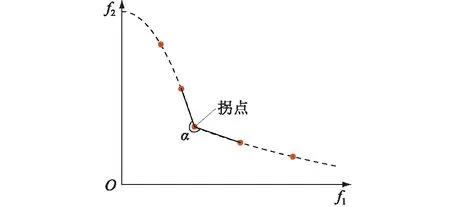
图1 基于角度选择的拐点Fig.1 Inflection point based on angle selection

因此，在没有任何先验知识的前提下，可以将拐点处的解决方案当作多目标决策的最佳方案，这样能够使算法最终输出一个满意解，而无需决策者的参与。

2.3 自适应参数的调整策略

文中采用基于进化阶段的自适应方法作为个体交叉率与变异率的调整方法[20—22]。将种群的整个进化过程分为3个阶段，不同阶段个体交叉率与变异率都随进化代数的增加呈线性下降走向，直至在数值上与下一阶段的初始交叉率和变异率相等。自适应交叉率和变异率的模型具体如下。

(1) 当非支配解个数小于20时，个体交叉率和变异率的模型分别为：

(9)

(10)

(2) 当非支配解个数大于等于20时，个体交叉率不变，而变异率模型为：

(11)

式中：Pc为个体交叉率；Pc1，Pc2，Pc3分别为设定的各阶段的交叉率参数；Pm为个体变异率；Pm1，Pm2，Pm3，Pm4分别为设定的各阶段的变异率参数；β为变异率模型调节参数；K为算法的最大进化代数，K1=αK，K2=(1-α)K。0～K1为进化初期阶段，K1～K2为进化中期阶段，K2～K为进化后期阶段。

在种群进化前期，优秀解距离Pareto最优前沿较远，为保证群体的参与性，需要采用较大的变异率Pm，提高全局搜索能力，防止种群早熟；在进化中期，需要兼顾全局与局部的搜索特性，以便提高收敛的速度；在进化后期，种群中优秀解的数量居多，采用较大的交叉概率Pc，以提高局部搜索能力[23]。算法的详细流程如图2所示。

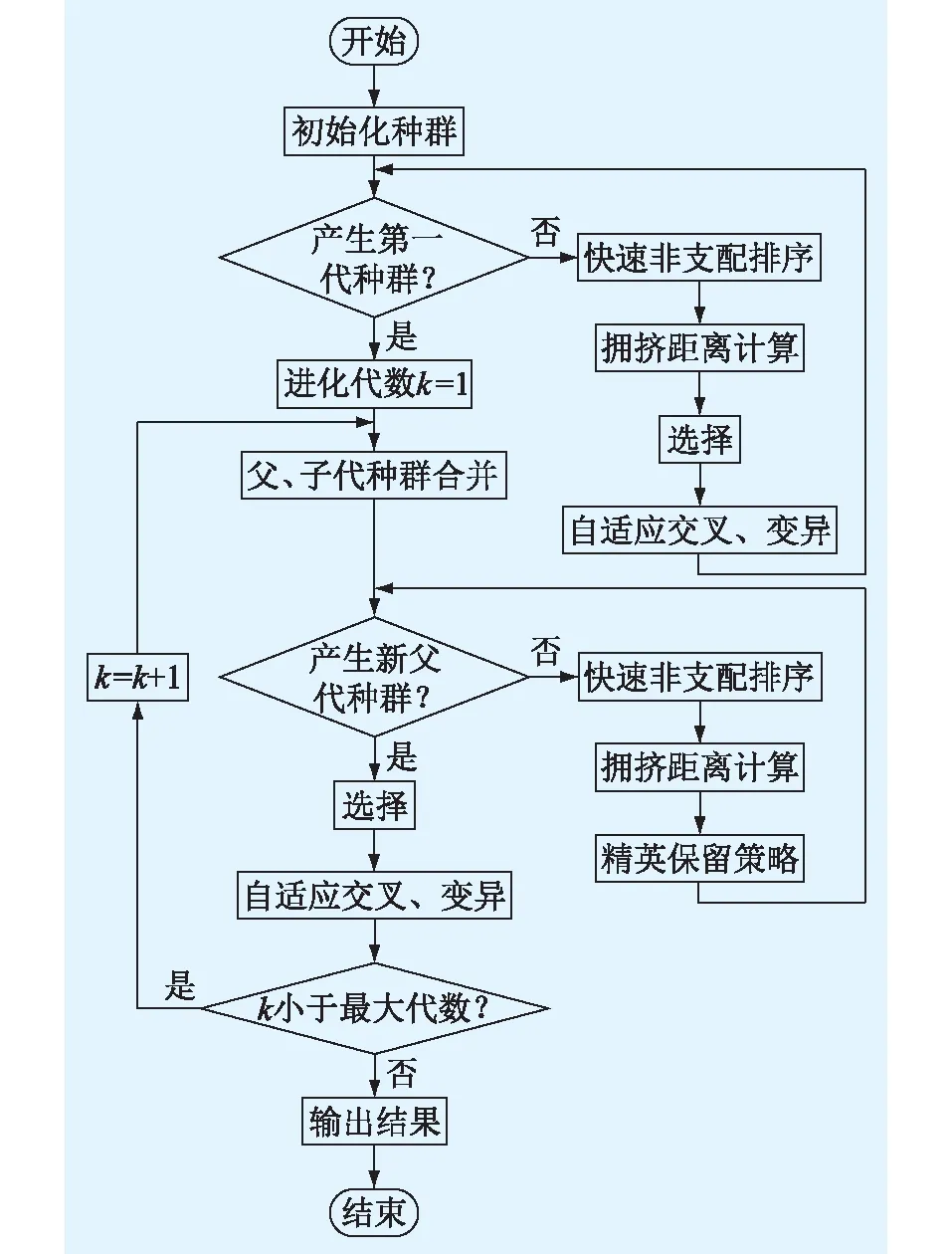
图2 改进的自适应NSGA-Ⅱ算法流程Fig.2 Process of improved adaptive NSGA-Ⅱ algorithm

3 算例分析

3.1 算例参数

以某镇某条实际配电线路为算例，图3为该线路简化图。假设某时间段配电网络中共发生10起故障，C1～C10为故障点所在位置，0为电源点，1～32为负荷节点。由于只有1个电源点，因此故障点后的节点将完全失电，各节点失电负荷功率和等级如表1、表2所示[24—25]。

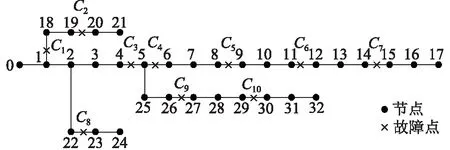
图3 某镇实际配电线路简化图Fig.3 Simplified diagram of actual distribution network in a town

对于各故障点后的负荷等级，按一级负荷权重w1=100，二级负荷权重w2=10，三级负荷权重w3=1设置。各故障点故障类型和预计抢修时间如表3所示[26]，故障点的地理坐标如表4所示，抢修中心o的地理坐标为(113.244 164,24.263 363)。

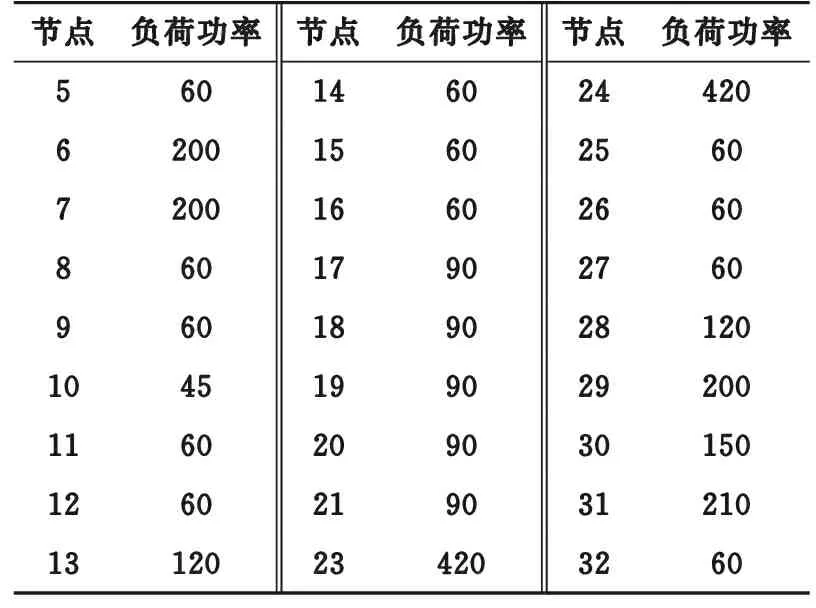
表1 各失电节点负荷功率Table 1 Load power of each power loss node kW

表2 各失电节点负荷等级Table 2 Load level of each power loss node

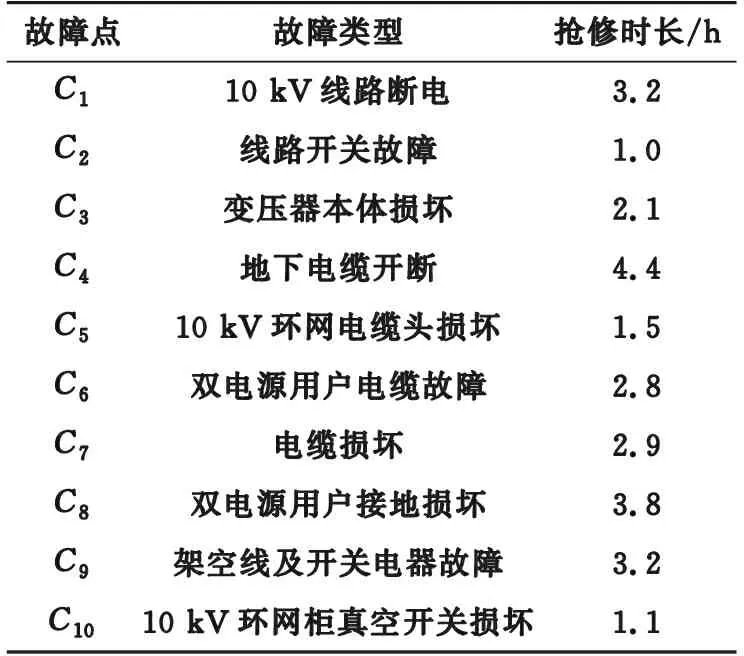
表3 各故障点故障类型和预计抢修时间Table 3 Fault types and expected repair time of each fault point

表4 各故障点地理坐标Table 4 Geographical coordinates of each fault point

3.2 算例求解

假设共有3个抢修能力相同的抢修班组，抢修班组在故障点间的行程速度为60 km/h，设置NSGA-Ⅱ算法的参数为[27—28]：种群规模100，最大进化代数200，自适应参数Pc1=0.6，Pc2=0.7，Pc3=0.9，Pm1=0.2，Pm2=0.4，Pm3=0.3，Pm4=0.1，α=0.25，β=0.6。运行算法程序，得到结果如图4所示。

图4 使用自适应参数策略的算法结果Fig.4 Results of algorithm using adaptive parameter strategy

图4(b)中，每一个点都代表一个Pareto最优解，每个最优解代表的抢修方案如表5所示。

表5 抢修方案展示Table 5 Emergency repair scheme

为得到最终的抢修方案，首先对表5中的2个目标函数值按式(12)进行标准化，标准化后的结果及每个方案的角度α如表6所示。

(12)

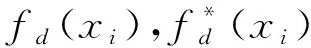
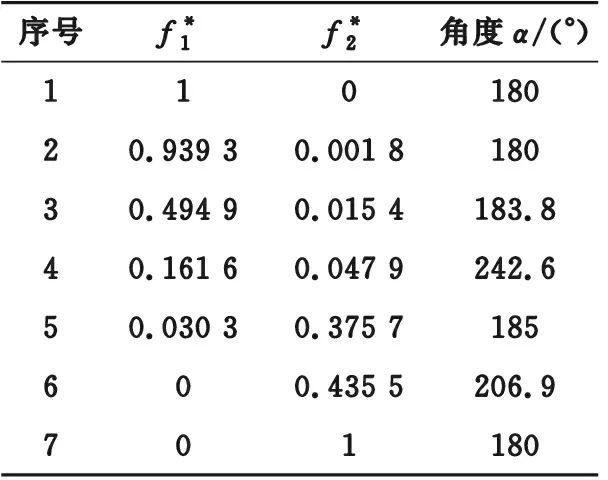
表6 标准化后的方案角度Table 6 The angle of schemes after standardization

根据前文所述的基于角度选择的拐点决策算法，显然点4为该优化问题的拐点，因此最终选择方案4为该抢修优化问题的最佳方案。

3.3 结果验证

3.3.1 基于角度选择的拐点决策的验证

从实际抢修经验来看，对高级别负荷的抢修程度更紧急。如图3和表2所示，故障点3、4、5、6、7、9的故障造成了一级负荷8、10、12、15、27失电，需要尽早修复。表5所示的7个可行方案中，方案1、2、3、4都将故障点3、4、5、6、7、9放入了各班组抢修顺序的前列，而方案5、6、7出于缩短抢修时间的考虑，都制定出了4→5→6→7的抢修顺序。

算例中最终选择方案4作为最佳抢修方案，与“对高级别负荷的抢修程度更紧急”这一实际抢修经验相符合。因此，文中所提基于角度选择的拐点决策算法适用于实际抢修工作，可以减轻决策人员的负担。

3.3.2 自适应参数调整策略的验证

若不采用自适应参数的调整策略，设置Pc=0.9，Pm=0.1，仿真结果如图5所示。由图5(b)可知，得到的Pareto最优解较少，分析图5(c)和图5(d)可知该算法早熟收敛，由于始终采用较大的交叉率和较小的变异率，容易陷入局部最优从而丢失部分Pareto最优解(与表5相比丢失方案1、2、3)。

图5 早熟收敛的算法结果Fig.5 Results of algorithm with premature convergence

设置Pc=0.6，Pm=0.4，仿真结果如图6所示。与表5相比丢失方案1、3，由于始终采用较小的交叉率和较大的变异率，搜索范围较大但是局部搜索性能不好，容易丢失某些Pareto最优解(得到了方案2、4，但丢失了方案3)。

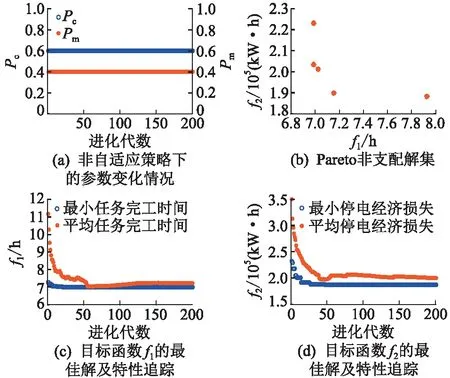
图6 局部搜索能力差的算法结果Fig.6 Results of algorithm with poor local search ability

根据2.3节所述，采用自适应参数的调整策略的搜索算法，在种群进化前期可具备较高的全局搜索能力，在进化中期可具备较高的收敛速度，在进化后期可具备较高的局部搜索能力。

4 结论

(1) 故障抢修任务中，不同地区的配电系统对各个目标的重要性存在差异。因此，不使用加权法而是采用非劣解生成法得到Pareto集，可以避免因权重设置的不合适而错过最优策略。

(2) NSGA-Ⅱ算法中引入自适应参数的调整策略，能提高种群进化前期的全局搜索能力以及进化后期的局部搜索能力，完成可行解的全面搜索。

(3) 在多目标优化中引入基于角度选择的拐点决策算法，可以直接从多个可行方案中选择最终的决策方案，从而减轻决策人员的负担，并且适用于实际抢修工作。