计及下垂控制的潮流计算研究综述

易文飞， 卜强生

(国网江苏省电力有限公司电力科学研究院，江苏 南京 211103)

0 引言

潮流计算是电力系统分析的基础。利用潮流计算得到的潮流分布，可对电网运行控制与电网状态进行在线分析与预测，因此电力系统要不断发展就必然要求潮流计算技术不断更新[1]。

随着电力市场化改革的不断推进、光伏与风力发电等分布式电源(distributed generation，DG)的大规模并网，以DG为代表的下垂控制设备占比逐渐增高，电力系统发生了以下变化：(1) 配电网潮流由辐射型网络变为多电源点型网络、由单向潮流变为双向潮流；(2) 运行特性的改变具有不确定性；(3) 以下垂控制方式运行时频率不再固定，相关线路参数随频率发生变化[2]。由此可见，DG接入虽给电网带来供电新活力，为电力负荷高峰提供支持，但其运行特性的多变性导致数学模型变得更为复杂，给潮流计算工作带来了挑战。当计算含有下垂控制特性设备的电网潮流时，现有研究都是先建立相应设备的精确模型[3]；再考虑不同类型的设备在运行特性上的区别，将具有下垂控制特性的设备或节点处理成常规潮流计算中的节点类型，即PQ节点、PV节点、平衡节点；最后列写潮流功率方程，选取合适的计算方法进行求解。

文中从电力系统中下垂控制的基本原理出发，首先分析了现有潮流计算对下垂控制节点的处理方法，然后从下垂控制模型、网络方程构建、元件参数频率变化、计算方法4个维度进行分析和总结，指出了现有建模和求解方法存在的问题。最后，结合电力系统潮流计算新需求，提出在建模方面建立统一化计算模型，在求解算法方面可采用数学规划方法进行求解，但须结合实际场景进一步完善。

1 电力系统下垂控制及其潮流计算

1.1 电力系统中的下垂控制

下垂控制是电力系统中微型电源的一种控制方式[4]，通过模拟传统同步发电机的外特性曲线(即有功-频率和无功-电压一次下垂曲线)，实现系统中各微型电源的功率平衡。

下垂控制方式运行下的设备只需要测量有功、无功、电压幅值、电压相角与频率等运行参数，按照给定的下垂控制曲线调整有功、无功输出，在无信息交互的情况下就可让电网频率稳定在给定数值范围内，同时各装置的电压符合各自的要求，并且有功、无功出力平衡；新增下垂控制的设备也只需按照该微电网参数制定下垂控制曲线，即可加入该网络运行。下垂控制是一种可以实现“即插即用”模式的控制方式[5—6]。

以正序网络中的P-ω、Q-V型下垂控制方式为例，其控制方程为：

(1)

式中：ωi为节点i的运行角频率值；Vi为节点i的电压幅值；ωi0，Vi0分别为节点i空载运行时的角频率与电压幅值；mPi，nQi分别为节点i的P-ω、Q-V型下垂控制系数；PGi，QGi分别为节点i注入电网的有功与无功功率。

由式(1)可知，下垂控制设备注入节点i的有功、无功功率为：

(2)

P-ω、Q-V型下垂控制特性曲线与控制框图分别见图1、图2。其中，f=ω/(2π)；U0，f0分别为空载运行时的电压和频率；Pin，Qin分别为输入有功和无功功率；ωout，Uout分别为输出角频率和电压。

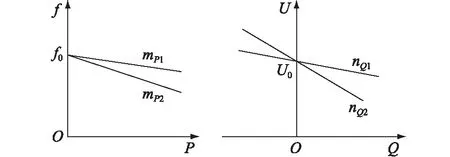
图1 P-ω和Q-V型下垂控制特性曲线Fig.1 P-ω and Q-V droop control characteristic curves

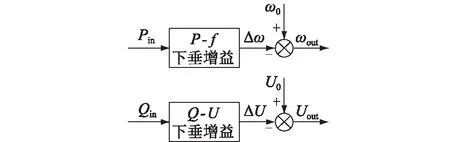
图2 P-ω和Q-V型下垂控制框图Fig.2 Block diagram of P-ω and Q-V droop control

此外，下垂控制还有P-V、Q-ω型控制方式，其特性曲线、控制方程及框图与上述类似。为建立更贴合电力系统实际运行的模型，下垂控制策略也在不断发展。文献[7]改进了P-ω型下垂控制，使得微电网孤岛运行中的瞬时有功功率分配更加合理；文献[8—9]考虑了设备下垂系数取值不固定，在求解过程中不断修正下垂控制系数；文献[10—12]则是针对不同类型的下垂控制设备，提出了计算与确定相应下垂系数的方法；文献[13]改进了下垂控制，使其能适应电力系统功率突变场景，保证系统平稳运行；文献[14]提出了在下垂控制曲线中设定合适的控制死区；文献[15]提出了应用于高压直流系统的改变电压基准的自适应下垂控制；文献[16]则是对引入虚拟阻抗的下垂控制进行了研究。

1.2 下垂控制潮流与动态潮流计算

对于一个给定网络结构、参数与运行限值的电力系统，常规潮流计算选取该系统稳态运行的某一时刻。假定该时刻系统频率为工频、系统中功率已由平衡节点平衡、各节点状态量遵循约束，则可通过常规潮流计算求解出这一时刻系统的详细运行状态[17]。

文中所述的计及下垂控制的潮流计算则是面向含有下垂控制设备的电力系统的详细运行状态求解。同样选取系统稳态运行的某一时刻，该时刻系统功率平衡，状态量遵循约束。不同于常规潮流，下垂控制潮流计算系统频率非固定，系统功率由有调节能力的电源共同平衡,且电源调节时遵循各自的下垂控制曲线。

同样涉及系统频率变化的还有动态潮流计算。动态潮流计算是假定在系统运行的某一时刻源-荷间仍存在不平衡功率，且不平衡功率由全体有备用容量的发电机与负荷共同调节，同时状态量满足必要约束，经过一个较小时间段后[18]，系统重新达到功率平衡这一过程的求解。

考虑下垂控制的潮流与动态潮流相同之处在于引起频率变化的不平衡功率不再由平衡节点单独承担[19]；动态潮流中不平衡功率的一次调频分配策略与文中所述的交流系统中的P-ω型下垂控制相似[20—21]。不同之处在于，动态潮流主要考虑电力系统中源-荷有功功率不平衡及频率变化，且主要针对电网中的交流系统，而在计算过程中较少涉及电网电压变化[22—23]；考虑下垂控制的潮流计算则是对加入下垂控制设备的系统在某一时刻详细运行状态的求取，包括系统电压和无功功率。计及下垂控制的潮流计算面向电力系统源网荷储的各个环节，如P-V型下垂控制的新能源发电系统[24—25]、主配一体化电网、交直流混合电网、储能电站等。

1.3 下垂控制潮流计算的应用场景

根据电力系统中不同的网络规模及运行方式，计及下垂控制的潮流计算主要应用于以下3种场景：

(1) 含下垂控制设备的配电网。下垂控制设备的规模相对较小，因此直接通过公共连接点(point of common coupling，PCC)接入配电网。下垂控制设备的接入对配电网运行影响较大[26—27]。

(2) 微电网并网运行。DG所在地理位置比较集中时，可以考虑用一定的控制策略将其与部分网络及负荷整合为一体，称为微电网[28]。微电网主要有交流微电网与交直流混合微电网2种类型。对于大电网而言，以微电网的形式接入配电网运行可视为只增加了一个节点，较为容易处理。

(3) 微电网孤岛运行。微电网自成独立系统，脱离大电网运行，此时微电网频率不再固定[29—30]。对于微电网孤岛运行中的下垂控制设备处理方式较多，现有研究表明孤岛运行时的计算方法已取得较多成果，但仍须改进。

2 下垂控制设备的模型与潮流方程

2.1 下垂控制设备及处理

电力系统中具有下垂控制特性的设备种类繁多，而在计及下垂控制潮流计算的现有研究中主要考虑风力发电、光伏发电、微型燃气轮机、燃料电池电站、分布式储能装置、电压源型换流器(voltage source converter，VSC)等。按照运行方式的不同，上述设备主要分为P-Q型、P-V型、P-I型、P-Q(V)型、下垂控制型5种类型[31—32]。

下垂控制型设备注入电网的有功、无功功率按式(2)计算，将式(2)进行变形得到：

mPiPGi=ωi0-ωi

(3)

由于稳态时系统中只有一个频率，故对于各个节点，式(3)必须成立，即同一系统内的下垂控制型设备需要满足如下条件：

mP1PG1=mP2PG2=…=mPiPGi

(4)

在常规潮流计算中，电力系统的节点一般按照运行特性分为PQ节点、PV节点、平衡节点3种[2]。在计及下垂控制的潮流计算中，对外呈下垂控制特性的节点可称为下垂节点，下垂节点的有功、无功功率可按式(2)加入网络方程。

2.2 考虑下垂控制的网络设备潮流模型

对考虑下垂控制的交流系统进行潮流计算时，所采取的数学模型与传统模型的设定基本一致，线路与变压器均采用π型等值电路。

交流系统中的负荷模型采用静态负荷模型[1]，引入下垂控制时须考虑频率与电压的变化，此时电网负荷模型表示为：

(5)

式中：PLi，QLi分别为节点i的负荷有功与无功功率；PiN，QiN分别为节点i的额定有功与无功功率；f，fN分别为节点i的实际频率与额定频率；Kp f，Kq f分别为频率对有功、无功的影响系数；α，β分别为电压对有功、无功的影响系数。直流系统中的负荷考虑电压变化，不考虑频率变化影响，即直流负荷模型为式(5)除去频率项的形式。

现有涉及下垂控制潮流计算的文献中，交直流混合系统的VSC设备均使用脉宽调制(pulse width modulation，PWM)技术，如图3所示，未见其他调制方式，其模型表示如下：

(6)

式中：UVSC,AC，δVSC,AC分别为交流侧的电压幅值与相角；UVSC,DC，δDC分别为直流侧的电压幅值与相角；M为PWM技术中的调制比。VSC的有功、无功功率可以参考发电机的功角特性方程进行求取。图3中，C为电容值;UDC为直流侧电压；ZAC为交流侧输入阻抗；S1、S2为VSC。

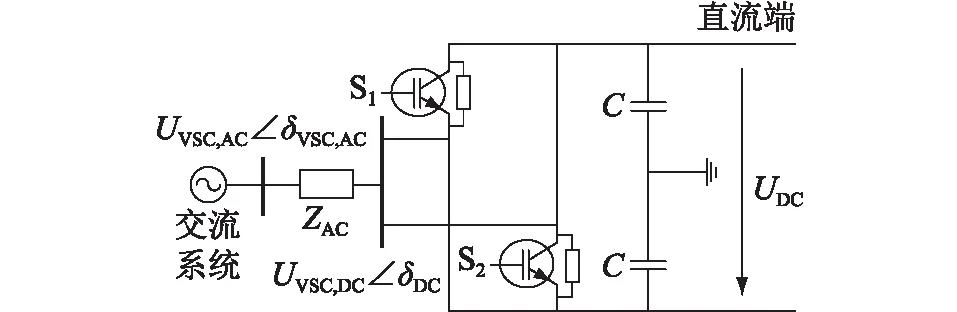
图3 VSC等效电路Fig.3 Equivalent circuit of VSC

2.3 计及下垂控制的潮流方程

电力系统中节点功率方程一般表示为：

(7)

式中：FPi，FQi分别为节点i注入的有功功率之和、无功功率之和；Pi，Qi分别为其余节点注入节点i的有功、无功功率。

交流系统的节点功率方程具体表示为：

(8)

式中：Pis，Qis分别为节点i电源有功和无功功率；Gij，Bij分别为支路ij阻抗和导纳；ei，fi为节点i电压的极坐标值；ej，fj为节点j电压的极坐标值。

下垂控制设备对所在节点注入如式(2)所示的功率，则该节点功率方程可以表示为：

(9)

式中：PDis，QDis分别为下垂控制设备输出的有功、无功功率。

当系统为交直流混合系统时，交直流系统联结处功率方程则变为：

(10)

式中：PGi,AC，QGi,AC分别为交流侧节点i注入的电源有功、无功功率；PLi,AC，QLi,AC分别为交流侧节点i注入的负荷有功、无功功率；Pi,AC，Qi,AC分别为交流侧其余节点注入节点i的负荷有功、无功功率；PVSC，QVSC分别为交直流系统联结处换流器的有功、无功功率(以VSC为例)。

3 下垂控制对潮流计算的影响

当电力系统考虑下垂控制后，潮流计算须考虑出现新变化量所产生的影响。直流系统中状态量较少，下垂控制对其潮流计算影响相对较小；而交流系统计及下垂控制后，常规潮流计算中平衡节点的电压与系统频率由恒定变为可变。第3章归纳了现有研究对交流系统中这2个变化的处理。

3.1 平衡节点问题

下垂控制设备并网运行或微电网并网运行时，不必考虑系统中的平衡节点问题。在计及下垂控制的潮流计算方法研究中，当含下垂控制设备的微电网孤岛运行时，按照有无常规潮流计算中的平衡节点可分为2种方式。

(1) 取消平衡节点的设定。方程列写方式与常规潮流计算方程有所不同，频率作为变量需要在潮流计算中求解，因此雅克比矩阵中也相应增加有功、无功关于频率的一阶偏导数[33]。此外，系统仍需一个电压相角参考节点作为潮流计算结束后各节点相角更新的参考，一般取节点编号完成后的1号节点，参考相角设为0或自定义[34—35]。

(2) 保留平衡节点的设定。该种方式在微电网孤岛运行时使用较少，并网运行时使用较多。文献[36]选取容量较大的DG节点作为潮流计算中的平衡节点，电压幅值与相角给定，与常规潮流计算的平衡节点一致；文献[37]也保留了平衡节点，但仅在潮流计算环节中设定平衡节点的电压幅值与相角不变，在下垂控制更新状态量环节中，平衡节点仍须修正电压幅值，即该文中的平衡节点对于整个计算过程而言仅作为其他节点的相位参考。

3.2 系统频率的更新

在电力系统潮流计算中，随着下垂节点的引入，常规潮流计算未提及的频率问题势必要纳入考虑范围。下垂控制的潮流计算主要分为下垂控制设备接入配电网运行、组成微电网后并网运行、组成微电网后孤岛运行3种情况。现有研究成果显示，仅最后一种运行方式考虑了系统的频率问题。

系统频率成为变量时，计算或迭代须及时更新系统频率。一个交流系统只有一个稳态频率[2]，在现有研究中，频率更新的主要方式有以下2种。

(1) 系统有平衡节点时，需要计算平衡节点的等效有功功率，根据平衡节点的下垂控制曲线更新系统频率。由上文可知，同一系统内以下垂控制特性运行的设备须满足式(4)，令下垂节点总数n>2，取其中一个下垂节点k作为平衡节点，则有：

(11)

每个等式两边各自同乘等式左边节点外剩余节点的有功下垂控制系数，并将所有等式的左右两边累加，整理得到PGk为：

(12)

式中：l为下垂节点数。算得PGk之后代入式(1)，更新系统的频率。

(2) 系统中无平衡节点，在列写潮流方程时，各元件模型均考虑频率特性，将频率作为一个变量加入方程进行求解，现有研究中这种更新方式使用较多。以一个总计n个节点的含下垂节点型DG的电网系统为例：系统中前m个节点是PQ节点，节点m+1到m+k是k个PV节点，节点m+k+1到n是d个下垂节点，取节点1作为系统电压相角参考点(可设δ1=0)，系统频率参与计算。

根据式(7)、式(8)可以得出上述系统的节点功率方程组为：

(13)

式中：FP(·)，FQ(·)分别为节点有功、无功功率的函数；ω，Um，δn分别为对应节点的角频率、电压和相角。式(13)的功率方程总数为n+m+d，系统待求量总数为n+m+d，两者数量相等，通过牛顿-拉夫逊法(简称牛拉法)或其他求解方法可以求得待求量，系统频率作为其中一个待求量能得到更新。

3.3 元件参数的频率变化特性

电力系统潮流计算中，交流网络的线路参数、变压器参数、电力负荷均与系统频率密切相关。含下垂控制设备的配电网或微电网并网运行时，不需要考虑频率变化的影响；而微电网孤岛运行时频率不再恒定，此时必须考虑参数随频率的动态变化。

当线路频率变化时，其参数变化为：

(14)

式中：ωN为电网额定频率；ωt-1为迭代t-1次后的频率；xl,t，bl,t分别为第t次迭代开始时的电抗与电纳值；xl,0，bl,0分别为额定频率下的电抗与电纳值。

变压器考虑频率变化时，其等值参数计算涉及到的短路电抗则同式(14)中的线路电抗一样处理。

现有研究在进行潮流计算时，对计及下垂控制时的元件参数随频率变化这一方面关注较少，大部分研究均默认线路参数(导纳矩阵)不变。文献[33]中电力负荷模型考虑了频率效应，但并未提及线路参数与频率的关系；文献[38]提及了线路参数随频率变化的关系，但后续给出的计算流程中并未体现出导纳矩阵随频率更新的环节。虽然计及下垂控制的潮流计算得到的是最终处于稳态时的各节点状态，可以一定程度上忽略频率对元件参数的影响，但应当考虑潮流计算过程中因频率变化所致的参数变化对单次迭代计算结果、计算速度及收敛性能造成的影响。

4 下垂控制的潮流方程求解方法

计及下垂控制的潮流计算方法是在常规潮流计算方法中考虑了下垂控制关系。含下垂控制设备的交流系统节点功率表达式中含有系统频率与节点电压，考虑到潮流计算是对某一时刻潮流分布的求解，一般默认这类节点的功率与电压在单次迭代中不发生变化，因此可在单次迭代过程中令有功功率与无功功率(或有功功率与电压幅值、电压幅值与相角)恒定。在求解过程中这类节点可被视为常规潮流计算中的PQ节点(或PV节点、平衡节点)，从而列写潮流方程进行求解。

如文中1.3节所述，计及下垂控制的潮流计算场景中微电网主要有并网运行、孤岛运行2种模式，因此现有研究多以某一种运行模式与某一系统类型为出发点，研究的计算方法有：以直接法、前推回代法、序分量求解法等为代表的计及配电网特性的计算方法；面向单一网络类型的经典牛拉法；以信赖域算法为代表的新型求解方法。上述求解方法所面向的对象存在一定程度的交叉与重合，故文中从数学方法角度将计及下垂控制的潮流计算方法分为统一迭代求解法、分步式求解法及数学规划求解法3类，如图4所示。

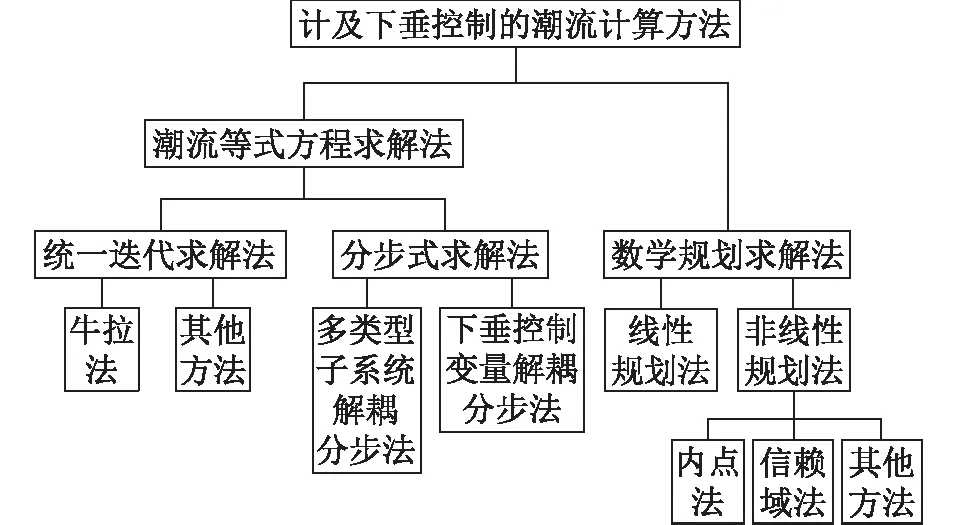
图4 下垂控制潮流计算方法Fig.4 Calculation methods for droop control power flow

4.1 统一迭代求解法

统一迭代求解法是将整个系统的状态量(包含系统频率)作为变量，建立统一的潮流方程，进行迭代求解。统一迭代求解法主要用于系统类型较少的大电网场景，最常见方法为牛拉法，其主要原理是将非线性方程逐次线性化逼近求解[39]，求解式(15)的线性方程。

F(X(t))=-J(t)ΔX(t)

(15)

式中：F(X(t))为潮流函数；J(t)为求解系数；ΔX(t)为状态变化量。若式(15)满足式(16)中任一条件即可判定为潮流收敛，完成潮流的求解。

(16)

计及下垂控制的潮流求解时，系统频率作为待求量在方程组中求解，计算时下垂节点可按先前所述，视为PQ节点、PV节点或平衡节点中的一种或几种，则牛拉法的潮流方程矩阵形式为：

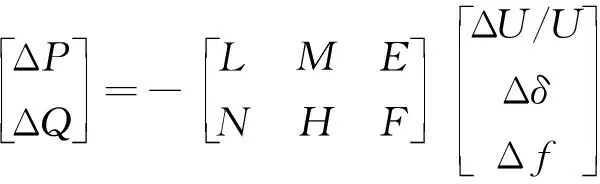
(17)

式中：ΔP，ΔQ分别为每次迭代过程中有功、无功变化量；ΔU，Δδ，Δf分别为迭代过程中电压、相角和频率变化量。矩阵方程中的雅克比矩阵元素L，M，N，H含义与常规潮流计算相同，新增元素E与F分别为：

(18)

式中：ΔPi，ΔQi分别为每次迭代过程中节点i的有功、无功变化量。系统有下垂节点时须相应增加功率修正方程，频率须在方程组中求解，所以状态变化量中多出Δf这一待求量。

在现有含下垂控制的潮流计算方法的研究中，文献[40]将牛拉法用于计算孤岛运行时的交直流混合微电网；但也有部分研究对牛拉法进行改进，使之更适合含下垂节点的潮流计算，如文献[33]在常规潮流计算节点的设定上去除了平衡节点，由具备调节能力的下垂控制电源共同承担不平衡功率，但在微电网孤岛运行中该方法可能存在雅克比矩阵奇异导致潮流不收敛的情况。文献[41]在牛拉法的基础上考虑潮流中的递阶控制，并对雅克比矩阵进行重新推导，提高了牛拉法的收敛性，但该方法单次计算量大、单次计算时间长。为应对牛拉法易出现的雅克比矩阵奇异问题，文献[42]提出了引入加权系数的牛拉法，单次计算时间略长于经典牛拉法，但迭代次数减少，整体收敛时间优于经典牛拉法；文献[43]则引入最小二乘求解的辅助因子，提升了计算效率与初值鲁棒性，减少了迭代次数。文献[44]提出了一种三相解耦的序分量求解方法，减少了雅克比矩阵的计算量，提高了求解速度。进行三相解耦的求解方法可以适应三相不平衡的配电网，但其求解对象为稳态潮流且未考虑微电网孤岛运行时节点状态量与元件参数变化，有进一步研究的空间。文献[45]以带新型线性搜索三步LM算法(three-steps Levenberg Marquardt algorithm with a new line search，NTLM)为基础建立统一潮流模型以解决雅克比矩阵可能发生奇异的问题。

统一迭代求解法作为系统整体迭代求解的方法，考虑了不同系统或状态量间的耦合关系，使得建立的统一模型更加精确，故单次迭代求得的解相比其他方法更靠近真实解。随着电力系统的发展，不同类型系统之间的耦合关系也更加复杂，建立统一模型的难度将不断增加，且单次迭代计算量较大。当系统规模扩大时，其计算量的迅速扩大将成为难题。对于复杂的下垂控制潮流，统一迭代求解法更适合为新的求解方法提供收敛速度与计算效率的参照。

4.2 分步式求解法

统一求解法对于含不同类型子系统的混合电力系统的建模难度较大，现有研究中提出一种将电力系统中的子系统解耦，以交替迭代方式进行求解的分步式求解法。该方法优势在于子系统解耦后单独建模难度显著降低，主要用于处理交直流电网耦合环节VSC以及交直流混合电网中含下垂控制设备的直流电网的场景。

文献[46]将直流系统的下垂控制以节点电流关系求解，从VSC处进行交直流系统解耦，与交流系统的牛拉法进行分步迭代；文献[47]则更充分地考虑了VSC模型与控制方式，解耦后分步交替迭代进行求解；文献[48]处理直流系统的下垂控制并进行交直流系统解耦后，交流系统使用改进XB型快速求解法，提升了整体的求解速度；文献[49]不仅对交直流系统解耦进行了分步求解，还对交流系统中的电压稳定与无功平衡进行了分步处理求解，更好地控制了混合电网的电压。

此外，还存在一种借鉴奔德斯分解思想的[50]、将处于下垂控制关系的变量进行解耦后交替迭代的分步式求解法。该方法主要面向考虑下垂控制的单一类型系统，根据计算过程中系统是否设置实际平衡节点，将其分为2类。

(1) 含实际平衡节点的分步式求解法。将单次迭代过程分解为2个步骤，即：步骤一，常规迭代计算；步骤二，系统频率更新与基于下垂控制方程的设备功率计算。为减少雅克比矩阵阶数以提升计算速度，在步骤一中可以选择一个下垂节点作为平衡节点，其余下垂节点均视为PV节点[37]。PV节点的有功功率与电压幅值、平衡节点的电压幅值与相角为上次迭代中步骤二的更新值；步骤二根据下垂控制曲线用步骤一求得的功率更新系统频率与节点电压。此外，第一次迭代时状态量为给定的系统初值。步骤二系统频率更新时使用的平衡节点有功功率按式(12)求得，求得系统频率后按式(2)更新PV节点的有功功率；步骤一中求得的无功功率根据式(2)更新PV节点的电压幅值，2个子问题交替迭代进行求解。

文献[37]使用了含平衡节点的解耦分步方法求解算例，如图5所示。潮流收敛所需迭代次数较少，在其第二步下垂控制更新中存在一个问题未交待清楚：含平衡节点的潮流计算可以直接求得平衡节点的功率，而文中却以推导得出的式(12)作为平衡节点的有功功率，并未说明2种方式所求有功功率的差异或直接求得的平衡节点有功功率不能用来更新频率的原因。

图5 含平衡节点的两步式求解Fig.5 Two-step solution with balance node

(2) 虚拟平衡节点的分步式求解法。该方法在系统中设置虚拟平衡节点，设置点一般为微电网并网点或微电网某一节点附近。求解时首先将虚拟平衡节点视为微电网的平衡节点，进行常规潮流计算，求得虚拟平衡节点功率；然后，由全体有调节能力的DG平衡该功率，按各自的下垂控制曲线进行功率分配；最后，完成系统频率与各节点电压幅值的更新，进行交替迭代，完成潮流的求解。该方法被用于计及下垂控制的配电网潮流计算中，如文献[51]在进行变量解耦后，以前推回代法进行计及下垂控制的配电网潮流计算；文献[35]则是分步后以直接法计算含下垂控制的配电网三相不平衡潮流。

如上所述，现有研究中的分步式求解法基本可分为子系统解耦与节点状态变量解耦2个维度。研究表明交直流系统解耦后的交替迭代求解法相比统一迭代求解法能更好建立模型与方程，更适合求解多类型子系统混合电网。将下垂控制变量进行解耦，降低了求解过程的复杂程度，在进行常规迭代计算时可借鉴现有的计算方法，仅须增加下垂控制功率分配与频率电压更新环节，减小了编程实现的难度。常规迭代计算部分可使用常规潮流计算方法，若用快速求解法可缩短潮流整体收敛时间。

4.3 数学规划求解法

数学规划求解法为在给定限制区域中寻求给定目标函数的最小或最大值的一种数学方法，一般可分为线性规划法和非线性规划法2种。

数学规划求解法稳定性高，主要用于无平衡节点或初值较差等原因导致等式方程求解类方法不易求解的潮流计算场景。计及下垂控制的潮流方程一般为非线性方程，可将潮流方程转化为目标函数，即将非线性方程求解问题转化为非线性规划极值的求解问题，此时可将非线性规划法的求解方式应用到下垂控制潮流计算中。现有研究中相关问题所使用的非线性规划求解法有内点法[52—53]、信赖域法[34,54]等。

潮流计算由非线性方程组求解问题转变成非线性规划问题，可表示为minF(X)。常规潮流求解时的潮流函数F(X)可由式(6)与式(9)的功率方程进行构造，而计及下垂控制的潮流计算新增了下垂节点，可将下垂节点按式(2)加入方程，参考式(12)进行构造，最终方程可表示为：

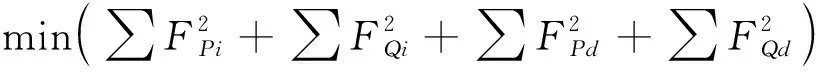
(19)

式中：X为状态变量矩阵，X=[x1x2…xn]；i为PQ节点、PV节点的编号；d为下垂节点的编号。

非线性规划法的特点为潮流求解过程不易发散，对初值敏感程度较低，在潮流方程为病态的情况下也易求得解，潮流无解时也会收敛至某个值或在可行域内不断寻解。该方法所呈现的求解结果可以为潮流有无解提供判断依据[39]。

文献[34]中的BFGS信赖域法就是一种无约束非线性规划求解方法，其收敛性能优异且对初值不敏感，避免了牛拉法初值不当无法求解的问题。但该方法须重新计算每次的海森矩阵，即使文中构造了海森矩阵的近似矩阵，计算量仍大于牛拉法的雅克比矩阵，且收敛判据精度高时迭代次数较多，因此求解效率低于牛拉法。文献[54]对信赖域算法进行了以雅克比矩阵代替海森矩阵构造信赖域子问题的改进，较文献[34]提高了收敛速度且保持了方法本身的其他优点。

数学规划求解法是在给定约束条件内找到极值或最优解，相对非线性潮流等式方程更易求得解，但该类方法计算效率较低，在寻解方式选择不当时更为突出，有进一步研究的空间。

5 未来研究展望

现有研究所提出的计及下垂控制的潮流计算方法各有优缺点，其精确建模与准确计算的方法正在日趋完善，可以进一步研究与考虑以下内容：

(1) 对于统一迭代求解法，可进一步研究迭代算法的优化处理，降低其对初值敏感度并缩短单次迭代计算时间。此外可研究PQ分解法、改进牛拉法等快速求解方法对于计及下垂控制的潮流计算的适应性；研究相应计算方法的具体改进措施，使之能在计及下垂控制的潮流计算中应用。

(2) 当下垂控制设备接入交流系统，认为系统频率可变时，对于某一种潮流计算方法，若计算时考虑元件参数频率变化特性，则每次迭代过程中导纳矩阵均随频率变化，其性能会受到一定影响。因此，须进一步研究这一情形对求解方法性能及导纳矩阵变化所得的计算结果的影响程度。

(3) 电动汽车、储能与新能源发电等设备大量并网。由于这些设备数量众多且分散地域广，不易统一控制，下垂控制成为这类新型设备参与电网互动的首选控制方式，因此未来计及下垂控制的潮流计算也需要将这些新型设备纳入计算当中。

(4) 虚拟同步发电机、虚拟电厂等技术的发展进一步拓展了下垂控制的应用场景，后续也需要针对性地开展相关研究。

6 结论

随着下垂控制设备的大规模并网、电网中的变化因素逐渐增多，一定程度上为电力系统运行与分析带来新考验，而计及下垂控制的潮流计算将是电网运行与状态分析的有效手段。文中从下垂控制模型、网络方程构建、元件参数的频率变化、计算方法4个方面对现有研究进行综述，可得出以下结论：

(1) 目前计及下垂控制的潮流计算的应用场景主要为孤岛运行模式的微电网。微电网中不同运行特性的下垂控制设备参与潮流计算需要不同的处理，但目前尚未有统一的下垂控制设备潮流模型构建方法。

(2) 对于单类型电网系统，可以使用变量解耦的方式将频率从控制关系中取出，单独进行求解更新，或将频率等下垂控制变量放进潮流目标方程以数学规划求解法进行求解。对于主配一体化、交直流等多类型混合电网可以使用统一迭代法、分步式求解法与数学规划求解法。

(3) 统一迭代求解法建模精度高，其中牛拉法应用较多、收敛速度快，但对初值要求较高且存在雅克比矩阵奇异问题。因此，需要进一步研究牛拉法的优化方法及其他适合统一迭代求解的计算方法。

(4) 分步式求解法对于混合系统而言建模难度低，解耦处理合适时潮流收敛效率高于统一迭代求解法，但存在交替迭代误差、迭代次数较多的问题，有进一步研究空间。

(5) 数学规划求解法目前在下垂控制潮流的应用较少，相对于非线性潮流等式方程求解类方法，对初值相对不敏感，更易求得有效解，但存在迭代次数多与计算量较大的问题，可进一步研究寻解与优化方式。

随着国家碳达峰与碳中和工作的稳步推进，新能源发电与电动汽车等新型设备在电网中的渗透率不断提高，下垂控制及其潮流计算方法将得到进一步完善与发展，未来有望在实际工程中得到广泛应用，为电力系统安全可靠运行提供有力支撑。