计算电容屏蔽电极位移测量的不确定度评估
王建波, 殷 聪, 钱 进, 刘忠有,黄 璐, 杨 雁, 陆祖良
(中国计量科学研究院,北京 100029)
1 引 言
基于“新”电磁原理(Lampard-Thompson原理)的计算电容装置,是电磁计量领域中基础的、不可或缺的精密实验系统[1,2]。它利用圆柱形电极对称排列形成的二维电场,通过测量屏蔽电极沿轴向的位移,实现对电容值的高准确度测量。它直接建立了SI单位中电容单位法拉与长度单位米之间的联系。2000年以来,国际计量局(BIPM)[3]、澳大利亚国家测量实验室(NMIA)[4]、美国标准技术研究院(NIST)[5]、中国计量科学研究院(NIM)[6~9]、法国国家计量院(LNE)[10]、加拿大国家研究院(NRC)等世界主要计量机构均着手研制新一代计算电容装置,以实现10-9量级甚至更优的测量不确定度指标,进一步提升电磁计量的水平[11]。
用计算电容装置实现微小电容值(0.2至 0.6 pF)精确测量的关键,在于对其屏蔽电极位移的高准确度测量。计算电容中采用锁定Fabry-Perot干涉仪来实现屏蔽电极在固定工作距离下位移变化的精密测量[12,13]。计算电容中使用的Fabry-Perot干涉仪,由安装于固定屏蔽电极顶部的凹面反射镜和可动屏蔽电极底部的平面镜构成,干涉仪的腔长,由私服锁定控制系统锁定在高稳定激光半波长的整数倍上[14,15]。因此,Fabry-Perot干涉仪在腔长改变情况下,其移动位移严格等于激光半波长的整数倍。即这种腔长锁定干涉仪能够实时补偿腔长的漂移,长时间保持腔长稳定,非常有利于计算电容值的精确测量。
本文建立了计算电容中屏蔽电极位移测量的模型;详细分析了位移测量中的各影响因素,并对其不确定度进行了评估和分析,最后获得了计算电容中屏蔽电极位移测量的总不确定度。
2 计算电容屏蔽电极位移测量方法
根据Lampard-Thompson原理,真空条件下,长度为L1和L2的导电柱面对应的交叉电容的平均值分别为C1和C2,且C1= ln 2×L1×ε0/π,C2=ln2×L2×ε0/π;交叉电容值仅与轴向长度L相关,如图1所示。

图1 计算电容中交叉电容示意图
工程实现中,由于准确测量长度L的绝对值难度较大,且存在端部效应的影响,所以通常采用测量电极位置的相对变化来精确测量电容的变化值,即:
ΔC=C1-C2=ln2×ΔL×ε0/π
=C0×ΔL
(1)
利用锁定Fabry-Perot干涉仪测量屏蔽电极位移ΔL的测量模型可表征为:
(2)
式中:λ为激光波长;ΔN为半波长的变化数;ε0为干涉仪锁定半波长整数倍的误差;εn为真空空气折射率的修正;εc为位移测量的余弦误差;εg为Gouy相移修正。
3 位移测量结果的影响因素分析
3.1 Fabry-Perot干涉仪锁定
计算电容中,Fabry-Perot干涉仪腔长锁定在λ/2的整数倍上,锁定效果是决定干涉仪性能的关键因素之一,锁定干涉仪的工作原理,可参考文献[12]。干涉仪锁定后的抖动越小,其腔长就越接近λ/2的整数倍。干涉仪锁定后的误差信号和透射峰的抖动如图2所示。干涉仪锁定引入的腔长相对标准不确定度可写为:

图2 干涉仪锁定后误差信号和透射光强的信号抖动
(3)
式中:δV为锁定后误差信号的抖动;Vp-p为误差信号的峰峰值;fFWHM为干涉仪透射峰的半高全宽;ν为激光频率。实验中,半高全宽和激光频率分别为50 MHz和474 THz,Vp-p为0.9 V,δV为0.013 V。计算得到,锁定引入的腔长相对标准不确定度为δLo/L=1.5×10-9。
2.2 激光波长
计算电容的Fabry-Perot干涉仪,采用经典兰姆凹陷稳频激光做直接入射光源,并引入碘稳频He-Ne激光实时测量兰姆凹陷稳频激光的波长[17]。与传统干涉仪不同之处在于,计算电容中的Fabry-Perot干涉仪处于锁定状态,其测量的位移为不连续的λ/2整数倍。在计算电容的一次测量过程(5次电容测量)中,需要完成4次干涉仪腔长的移动,每次腔长移动到电容电桥的工作点附件时,干涉仪锁定至兰姆凹陷稳频激光半波长的整数倍。此时,在不考虑其它因素干扰情况下,干涉仪腔长抖动与激光波长抖动成正比。在测量电容时,碘稳频激光同步测量并获得兰姆凹陷稳频激光波长的漂移曲线,如图3所示。激光的平均频差值为133.4 MHz,但在单次测量过程(6 min)中,激光波长漂移的标准为0.4 MHz。碘稳频激光自身引入的波长测量不确定度在10-11量级,对波长测量结果的影响可忽略。因此,由激光波长漂移引入的腔长测量不确定度为δλ/λ=0.4 MHz/474 THz=8.4×10-10。

图3 计算电容值测量过程中激光波长漂移结果
2.3 残余气体折射率
计算电容中的Fabry-Perot干涉仪工作在真空状态下。实验前,利用机械泵和分子泵组抽取密封腔内的真空度至10-4mbar。实验过程中,关闭泵组,整个密封腔的真空度维持在10-3mbar左右,根据Elden公式[18,19]:
(4)
式中:(n-1)tp为空气折射率;(n-1)s为标准条件下的空气折射率;p为气压,Torr(1 Torr=133.322 Pa);t为空气温度,℃。标准条件下的空气折射率(n-1)s满足:
(n-1)s×108=8 342.13+2 406 030·
(130-σ2)-1+15 997(38.9-σ2)-1
(5)
式中:σ为波数,μm-1。当激光波长λ=633 nm时,(n-1)s×108=2.765 2×104,将其代入式(4),得到(n-1)tp=3.6×10-10。因此,在测量计算电容屏蔽电极的位移过程中,残余气体引入的相对标准测量不确定度为:
(6)
2.4 测量余弦误差
余弦误差是指运动轴与激光束之间的夹角安装误差。测量位移与真实位移之间的差值可写为:
(7)
计算电容中Fabry-Perot干涉仪引入的余弦误差,包括有主体中心轴的复现、固定屏蔽电极的安装、辅助光路与实验光路的重合,以及可动电极的安装等4方面,下面分别介绍。
2.4.1 中心轴的复现
计算电容主体的安装调试过程中,以4根主电极的几何对称中心作为后续安装固定屏蔽电极和可移动屏蔽电极的唯一参考,如此,才能保证Fabry-Perot干涉仪的移动方向与主电极对称轴重合,最大程度地减小余弦误差。4根主电极安装于不锈钢圆筒内,并通过上、下圆形端板固定,如图4(a)所示。在上、下端板上的中心处,各有一个直径为7 mm的中心圆孔,4根主电极的安装调试就以上、下端板中心圆孔的中心线作为参考,利用特殊设计的电容传感器对4根主电极的平行性、相互之间的间距、倾斜量和扭摆角度进行大量、反复的测量和调整,最终可将主电极自身的安装误差控制在0.6×10-9以内。

图4 主电极中心轴复现
为了准确复现计算电容主电极的中心对称轴,以指导后续对Fabry-Perot干涉仪的安装,本文作者设计了如图4(b)所示的光路。可见,辅助激光器发出的光束穿过光阑后,利用光束提升装置将光束由上而下依次穿过两个定位圆片,产生的激光衍射光斑图像被CCD接收。两个定位圆片与不锈钢圆筒的上、下端板中心圆孔保持紧配合,且中心加工有直径为1 mm的小孔。当光束穿过第一个小孔时,衍射图像被CCD记录,并准确记录衍射图像中心坐标。装上第二个定位圆片后,通过CCD观察二次衍射的光斑图像,并记录衍射光斑中心坐标。根据惠更斯子波衍射理论,高斯激光束的小孔衍射特性在光轴附近可写为:
(8)

图5为经调整得到的衍射光斑在CCD的中心位置。当3种情况下,衍射光斑中心位置差小于20 μm时,辅助激光的入射方向与主电极的几何对称中心的夹角小于4×10-5rad。经过上述调试过程,可实现将计算电容的对称参考轴过渡至入射的辅助激光光线上。而后续的安装调试,将以辅助激光光线作为参考,进行屏蔽电极和可移动电极的调试。

图5 激光束的衍射光斑图像
2.4.2 固定电极的安装
固定屏蔽电极和主电极不锈钢圆筒的安装过程,如图6所示。对固定电极的安装,首先要保证固定屏蔽电极位于主电极的中心,然后,轻微调整屏蔽电极的角度,以确保其与辅助激光器的入射光垂直。实验中,利用特制的电容传感器实时测量屏蔽电极钉子头与主电极间中心的偏差,并反复轻微移动固定屏蔽电极的基盘,以使电极尽可能位于主电极的对称中心位置。
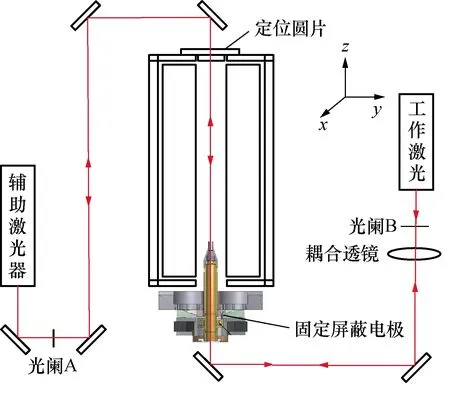
图6 固定屏蔽电极的调试示意图
对固定屏蔽电极反射镜角度的调节,是通过轻微移动球形凹面中的调节盘,使其围绕基盘的球心点轻微摆动来实现。通过观测反射圆环与光阑A中心孔的重合程度,可以判断凹面反射镜是否与辅助激光光线垂直。实验中,固定屏蔽电极凹面反射镜与光阑A的距离为3 m,反射圆环与光阑中心重合的判断不确定度在0.2 mm以内,因此,屏蔽电极凹面反射镜与辅助激光光线的夹角在0.067 mrad以内。
2.4.3 辅助光路与实验光路的重合
固定屏蔽电极安装调试完成后,需要将辅助激光光线的入射方向过渡到工作激光上,然后,才能进行可动屏蔽电极的安装和调试。由于固定屏蔽电极钉子头中凹面反射镜的反射率为85%,相当一部分辅助激光能透过反射镜片为工作激光入射方向的调整提供引导光线。由于固定屏蔽电极、可动屏蔽电极以及主电极在真空状态下工作,工作激光需经过带楔角入射窗(防止入射窗的前后表面产生寄生干涉)和45°反射镜(将光线由水平方向变为垂直方向)才能入射至Fabry-Perot干涉仪中。对工作激光与出射的辅助光线的共线调整,主要依靠光学平台上两个相距5 m的1 mm光阑来实现。两个光阑分别放置于辅助激光和工作激光的出射口处,以最大程度地增加光阑之间的距离,提高两束光重合程度的判断灵敏度。反复实验调整结果表明,工作激光和辅助激光与光阑中心重合的判断误差可以很好地被控制在0.3 mm以内,此条件下,两束光线的夹角在0.06 mrad以内,由该几何误差角引入的位移测量不确定度为1.8×10-9。
2.4.4 可动电极的安装
对可动屏蔽电极的安装调试,需要以工作激光的入射光线做参考,依据Fabry-Perot干涉仪透射光斑是否为TEM00模为标准,反复移动可动屏蔽电极,以保证在不同腔长(100~300 mm)下干涉仪的输出模式无变化。为了便于实时观测干涉仪的输出模式,及时通过真空电机调节可动屏蔽电极的倾斜角度,作者设计了如图7所示的安装调试系统。图7中,工作激光在PZT扫描电压作用下,能够大范围、周期性地扫描激光频率,使得Fabry-Perot干涉仪可周期性地透射出激光光斑。通过对透射光斑的分析,可以判断可动屏蔽电极在移动过程中的输出模式是否稳定,由此确定可动屏蔽电极的安装效果。
对可动屏蔽电极的调整,需要反复上、下移动,以观测干涉仪的透射光在移动过程中的透射曲线与输出光斑的形状。调整过程中,Fabry-Perot干涉仪的透射光强如图8(a)、图8(b)所示。若可动屏蔽电极底部的平面反射镜未与入射激光垂直,干涉仪的透射光强曲线会出现明显的多横模,如图8(a)所示,并在透过峰的旁边出现一系列较低的透过峰。此时,Fabry-Perot干涉仪因调整误差工作在多横模状态下会产生余弦调整误差,导致可动屏蔽电极位移的实际测量值将明显大于真实移动值。可动屏蔽电极调整到与入射光线垂直时,干涉仪的透射曲线呈系列尖峰状,如图8(b)所示,透过峰的底部无明显的寄生小尖峰。此时,Fabry-Perot干涉仪工作在基横模状态下,平面反射镜基本与入射光线垂直,可动屏蔽电极沿着4根主电极的对称轴上下移动。
为评估可动屏蔽电极的安装效果,取干涉仪的中间腔长L=200 mm进行计算。根据Fabry-Perot干涉仪的工作原理,干涉仪的透过率可写为:
(9)
正入射情况下,相位差与干涉仪的腔长相关,且Θ=4π L/λ。考虑干涉仪处于共振状态附近时,由平面反射镜安装误差引起干涉仪的透射率控制在T=95%以上,利用式(9)可计算得到:
Θ=2mπ ±δΘ; m=1,2,…
则计算得到δΘ=0.083rad。
假设平面反射镜与辅助光线存在安装误差角δθ,由此引起的腔长变化可写为δL=2ω′×δθ,其中ω′为干涉仪平面镜上通光孔径,则相位差的变化为:
δΘ=4πδL/λ=8π ω′δθ/λ
(10)
代入ω′=2.5mm,λ=633nm,得到δθ=0.02mrad,由此可知,可动电极安装误差对位移测量的影响为2.0×10-10。
2.4.5 整体安装的重复性
为了评估计算电容中光轴与计算电容机械轴重合性调整的方法,设计了如图9所示的模拟实验。小孔1和小孔2分别模拟实际调整过程中分别位于计算电容主体结构的上、下两端片。两个小孔的中心,在设计、加工和装调过程中均能保证与主体机械轴高度重合;加工和装配精度,可以保证两个小孔中心线与计算电容主体机械轴等效。因此,在调整实验中,只要能够做到准直光束穿过两个小孔中心,就可认为光轴与机械轴重合。考虑到光束的发散角及光强分布等因素,实验中采用He-Ne激光作为准直光束,实验过程如下:

图9 Fabry-Perot干涉仪轴向调整原理示意
调节反射镜1和反射镜2,使准直光束依次通过小孔1和小孔2的中心。如果小孔的孔径小于光斑半径时,则穿过小孔的光束会产生激光衍射环图样。如果衍射环不同心,则反复调整反射镜1和2,直至衍射环同心。反射镜3的作用,是为了将穿过小孔的激光束反射到更远处,使衍射图样变大,以便在接收屏上更准确地对衍射环进行观测。在实验中,通过一台光自准直仪对调整结果的角度值进行测量。图9中的反射镜1为双面反射镜,其正面作用是与反射镜2相配合,改变穿过小孔1和小孔2准直光束的入射角度,以保证每次调节完成后,在接收屏上看到对称的激光衍射环;其背面作用是将光自准直仪出射的光反射回来,以读取调整实验完成后反射镜角度的变化值。
对衍射环同心度的判断,实质上是对光轴与机械轴重合度的判断,也就是对光轴与机械轴之间夹角趋于零程度的判断。
实验中,采用孔径为1 mm的小孔,共进行11次重复性验证实验,实验结果如图10所示。由图10可知,采用准直激光加小孔衍射方法确定的光轴与机械轴夹角调整重复性的标准差为7.0″,由此引入的位移测量相对标准不确定度为5.8×10-10。

图10 Fabry-Perot干涉仪余弦误差模型实验结果
综合上述分析,计算电容中Fabry-Perot干涉仪的余弦误差为3.0×10-9。其具体分析示于表1。

表1 计算电容Fabry-Perot干涉仪余弦误差
2.5 Gouy相位修正
采用高斯激光束对屏蔽电极位移进行高准确度测量时,特别是当位移测量准确度达到10-8量级甚至更优时,高斯激光束弧形的等相位面对位移测量的影响就需要仔细评估。不同于理想的平面波光束传播,高斯激光束在传播过程中,其等相位面的曲率半径及其之间的距离,都会随传播距离的变化而改变。Fabry-Perot干涉仪中,高斯激光束的Gouy相移表示为腔内平面光场与高斯激光场之间的相位差。对于平行凹面腔,Gouy相移可写为:
φ(L)=arctan(L/zR)
(11)
式中:zR=π ω0/λ,为Fabry-Perot干涉仪的聚焦参数;ω0为高斯激光束的腰斑半径。式(10)可化简为:
(12)
式中:ρ为凹面反射镜的曲率半径。对式(11)进行曲率半径ρ的微分,可得到:
(13)
式(13)表示因干涉仪反射镜曲率半径ρ存在测量误差引起的Gouy相位的修正不确定度。取δρ/ρ=1%,ρ=5 000mm,λ=633nm,L1=111.3mm以及L2=316.3mm,计算得到δ(ΔLG)=0.15nm,δ(ΔLG)/ΔL=7.5×10-10。上述计算,要求对曲率半径的测量准确度要达到1%。对这个测量要求,采用激光共焦测量法完全可以满足。
2.7 计算电容测量结果的复现性
计算电容中的Fabry-Perot干涉仪是一种腔长锁定干涉仪。该干涉仪的腔长锁定至稳频激光器,因此腔长呈现台阶式状态,并严格等于激光半波长的整数倍。该干涉仪的位移测量就简化为测定激光半波长的整数倍。图11表示该干涉仪的台阶式位移过程。该干涉仪的位移以λ/2为步长,增加或减少λ/2的整数倍,并在任意的整数倍λ/2腔长上保持位置恒定。图11中的小插图,给出了该干涉仪保持腔长锁定时,其腔长的细微抖动,可见其抖动的峰峰值为0.4 nm。
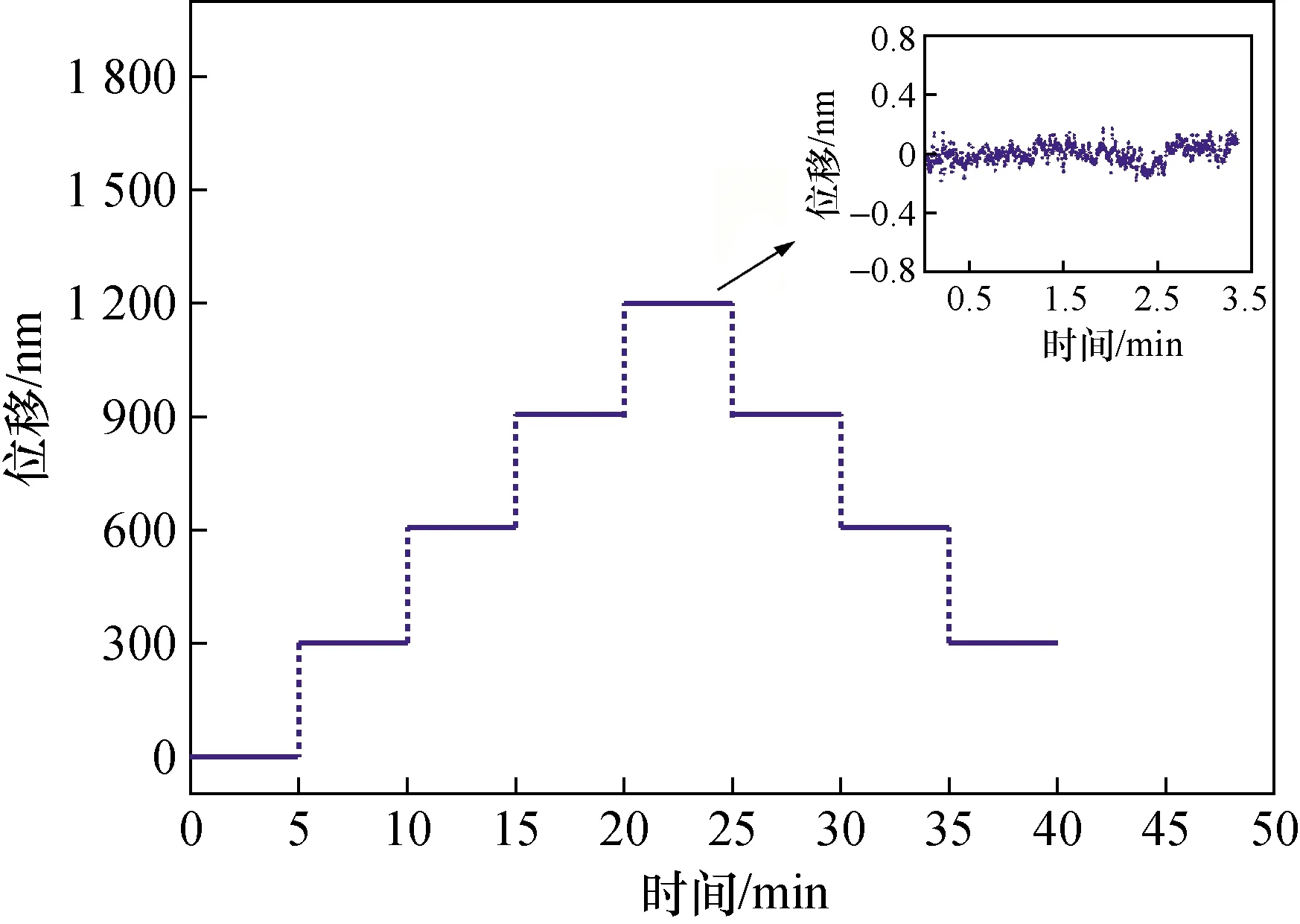
图11 锁定Fabry-Perot干涉仪台阶式位移过程
计算电容中,屏蔽电极干涉仪分别处于腔长111.3 mm和316.3 mm两种状态时,干涉仪的腔长锁定至高稳定激光,然后利用电容电桥对两种腔长下计算电容值(0.2 pF,0.6 pF)进行测量。为了评价屏蔽电极腔长锁定干涉仪位移测量的复现性,对计算电容传递至1 pF标准电容器的值进行了12次复现性测量,测量结果提供在表2中。依据计算电容值与干涉仪位移间的线性关系,如式(1)所示,计算电容值的复现性主要取决于干涉仪位移测量结果的复现性。实验结果表明,计算电容复现性的标准差为3.1×10-9。

表2 计算电容值测量1 pF标准电容器的复现性
4 屏蔽电极位移测量不确定度评估
依据上述不确定度分析,整理得到计算电容中Fabry-Perot腔长锁定干涉仪的位移测量不确定度各分量的大小,如表3所示,由其计算得到的合成总相对标准不确定度为4.7×10-9。

表3 位移测量不确定度分量大小
5 结 论
本文论述了计算电容中Fabry-Perot锁定干涉仪的不确定度分析和评定方法。具体围绕Fabry-Perot锁定干涉仪的5大影响因素,即残余气体折射率、余弦误差、激光波长、干涉仪锁定以及相位修正,逐项分析计算,并结合测量结果的重复性进行了综合评价。结果显示,计算电容中Fabry-Perot锁定干涉仪在200 mm移动距离下,其位移测量的相对标准不确定度为4.7×10-9。

