不同类型生态护坡在灌区渠道应用的多属性决策模型
肖合伟 裴文杰 谢高鹏
(江西省潦河工程管理局 宜春 330700)
在灌区开展渠道护坡建设的意义主要包括两方面:一是保护河道沿岸边坡,防止流水冲击、毁坏边坡;二是防止水渗入,降低水资源利用率。长期以来,灌区渠道普遍采用硬质化护坡技术,虽然有效地提高了边坡安全性和水资源利用率,但是同时也严重破坏了原有河岸生态转换、生物栖息地和绿色景观等功能。为了协调边坡安全、防渗、景观和生境条件等多方面,近年来生态护坡的概念被提出,并且得到了国内外普遍认可和广泛推行。本文基于多目标决策理论提出不同类型生态护坡在灌区渠道应用的多属性决策模型,以期为今后灌区渠道生态护坡建设工作提供借鉴参考。
1 生态护坡选择问题的数学概化
生态护坡选择问题可以概化成渠道、生态护坡两个集合中的个体根据相互间的适宜程度进行优化配置。决策者一方面需要考虑生态护坡与渠道的适宜程度,另一方面考虑在该渠道实施生态护坡后的效益,此外还需考虑实施的成本。
令 I={1,2,…,m},J={1,2,…,n},(m ≥ 2,n ≥2)。设有灌区渠道集合,记作A={A1,A2,…,Am},其中Ai为灌区渠道集合A 中第i 条渠道,i ∈I;设有生态护坡集,记作B={B1,B2,…,Bn},其中Bj为B中第j 项生态护坡技术,j ∈J。
就对渠道Ai而言,生态护坡技术Bj的效益为rij∈S,S=[smin,smax],其中smin、smax分别为对渠道而言,生态护坡效益的上、下限。此处效益通过生态护坡评价指标表征。灌区渠道A 关于生态护坡B 的效益矩阵为R=[rij]m×n。同理,就生态护坡集而言,每一项生态护坡技术对应每一条渠道也有一个应用的适宜程度,就生态护坡技术B 对灌区渠道A 的适宜度Bj矩阵为T=[tij]m×n,其中tij表示生态护坡技术对渠道Aj的适宜程度。
需要指出的是:生态护坡选择问题是灌区渠道与生态护坡技术之间的多对多匹配(m-n),可以将集合中的渠道或生态护坡技术视作多个具有相同属性的个体,这样就可以将多对多的匹配问题(m-n)转化成一对一(1-1)匹配,转化后的匹配问题的描述与计算将更加简便。
2 满意度、适宜度、成本矩阵的构造
本文采用将生态护坡措施实施效益与实施适宜程度进行排序和归一化处理,转化为满意度与适宜度,再进行排序的处理方式,这样处理的目的是:一是消除量纲不一致的情况;二是相同指标在不同渠道上的敏感程度可能存在较大差别,导致生态护坡匹配模型失效;三是为了描述和计算的简便,可以将集合中的渠道或生态护坡技术视作多个具有相同属性的个体,将多对多的动力匹配问题(m-n)转化成一对一(1-1)匹配,假设渠道2、渠道3(A2、A3)采用生态护坡技术B2 时的效益分别为6 和8,并且是渠道A2、A3 在诸多生态护坡技术中的最高,那么渠道A2、A3 对生态护坡技术B2 应该具有同等的匹配效力,进行动力需求满足排序计算可以实现。
在生态护坡选择匹配决策问题中,不失一般性,若渠道Ai将生态护坡技术Bj排在第1 位,那么记排序ai,j=1,渠道Ai对生态护坡技术Bj满意程度最高;渠道Ai将生态护坡技术Bk排在最末,那么记排序ai,k=n,渠道Ai对生态护坡技术Bk满意程度最低。此处的满意程度与适宜程度含义相似,采用如下公式计算渠道对生态护坡技术的满意度αi,j、生态护坡技术对渠道的适宜度βi,j:

在实际工程应用中,决策者除了需要考虑生态护坡技术实施的效用与适宜程度,还需实施的成本,在综合考虑生态护坡技术能够取得的效益与需要投入的成本的基础上,作出最优决策。设对渠道Ai实施生态护坡技术Bj的成本为ci,j,那么实施生态护坡技术的成本矩阵C 可以表示为:

考虑到下文需将生态护坡选择多目标优化模型转化求解,对重构措施成本也进行线性归一化,计算公式如下:

3 生态护坡选择多目标优化模型
3.1 目标函数
基于上文提出的渠道与生态护坡技术的满意度、适宜度、生态护坡技术实施成本等的定义与描述,可将生态护坡选择问题转化成如下多目标优化模型:
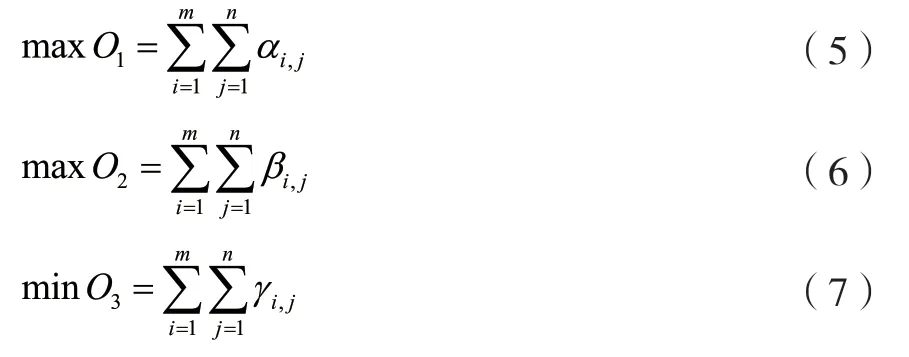
3.2 约束条件
生态护坡选择多目标优化模型的约束条件包括水量平衡约束、水位约束、流量约束、流速约束、水质约束、水质平衡约束、工程运行约束等。
3.2.1 水量平衡约束
灌区系统中,各单元需要遵循水量平衡约束,表达为下式所示:

式中:Wn,t为第n 个单元t 时段内的入流量;Qn,t为第n 个单元t 时段内的出流量;Sn,t+1为第n 个单元t 时段末的蓄水量;Sn,t为第n 个单元t 时段初的蓄水量;In,t为第n 个单元t 时段内的损失水量;Δt 为计算时段区间。
3.2.2 水位约束
灌区系统中,渠道等单元的水位在不同时期均需满足特定最低限和最高限要求,以满足防洪、供水、生态等需要,表达为下式所示:

式中:Zn,t为第n 个单元t 时段的水位;Zn,t,min为第n 个单元t 时段允许最低水位;Zn,t,max为第n 个单元t 时段允许最低水位。
3.2.3 流量约束
除水位约束外,渠道单元在不同时段也有相应流量、流速要求,一般与调度规则、工程特性等因素相关,表达为:

式中:Qn,t为第n 个单元t 时段的流量;Qn,t,min为第n 个单元t 时段允许的最小流量;Qn,t,max为第n个单元t 时段允许的最大流量。
3.2.4 流速约束

式中:Vn,t为第n 个单元t 时段的流速;Vn,t,min为第n 个单元t 时段允许的最小流速;Vn,t,max为第n个单元t 时段允许的最大流速。
3.2.5 水质约束

式中:qn,t为第n 个单元t 时段水质指标;qn,t,max为第n 个单元t 时段最低水质目标。
3.2.6 工程运行约束
主要包括灌区系统中诸多水利工程的过水能力、调度运行方式约束等。
3.3 模型求解
考虑到αi,j、βi,j、γi,j均为归一化值,因此可采用线性加权法动力匹配多目标优化模型转化为如下单目标优化模型求解:

在上述综合目标函数中,ω1、ω2、ω3为各分目标的权重系数,反映实际情况下各目标的重要程度,可依据实际问题给定,也可采用主观赋权法(如层次分析法)或客观赋权法(如熵权法)或者主客观相结合的方法确定。
转化后的模型求解可采用粒子群算法等求解方法或使用LINGO 软件求解。
4 结语
生态护坡技术在基本的保护边坡、提高水资源利用率功能的要求上,构筑能透水透气、生长植物的生态型护坡,强调安全性、稳定性、景观性、生态性、自然性和亲水性的协同。本文提出的不同类型生态护坡在灌区渠道应用的多属性决策模型可为今后灌区渠道生态护坡建设工作提供决策支持■

