铁磁板磁巴克豪森应力检测的解析模型*
张召泉 时朋朋 苟晓凡‡
1)(河海大学力学与材料学院,南京 211100)
2)(西安建筑科技大学土木工程学院,西安 710055)
作为评估铁磁材料性能及应力状态的重要无损检测技术之一,磁巴克豪森噪声方法可实现对材料早期结构损伤及相关应力状态的定量评价,应用前景广阔.此方法能否准确评估材料内部损伤及应力状态,关键在于能否建立合理有效的检测信号与材料内部应力分布之间的关系.为此,本文以铁磁板为例,沿板厚度方向激发信号,根据磁巴克豪森信号传播过程中的强度衰减效应,建立了铁磁板表面磁巴克豪森信号与材料内部应力定量关系的解析模型.基于已有实验结果的研究证实,本文理论模型能准确反映不同检测频率下铁磁板内部均匀应力值差异对检测信号的影响.而且,对于铁磁板内存在应力分布的情形,采用本文解析模型,研究得到了板内应力分布、铁磁板厚度、磁导率和电阻率等主要参数对铁磁板表面检测信号的影响规律.本文理论模型不仅揭示了基于磁巴克豪森噪声方法的铁磁材料应力检测机理,同时也为发展磁巴克豪森无损检测技术提供了合理有效的理论依据.
1 引言
铁磁材料具有良好的力学性能,被广泛应用于航空航天、道路桥梁、建筑工程等领域.材料在长期服役中形成的应力集中或局部损伤会直接影响工程结构的安全[1−3].采用先进应力无损检测方法,可在不影响材料及结构机械性能的前提下实现对其结构损伤和应力状态的准确评估,这对确保工程结构的服役安全[4−6]有着重要的理论和现实意义.磁巴克豪森噪声(magnetic Barkhausen noise,MBN)方法作为一种新型无损检测技术,通过磁畴不可逆运动激发的噪声信号,实现材料应力状态、损伤程度及微观组织变化特性的检测和评估[7−9].其主要优势在于可实现对材料疲劳、微裂纹等早期性能退化及应力状态的评估,应用前景广阔.
许多学者对MBN 的产生机制、影响因素等进行了研究[10−14].Kinser 等[10]通过测量和模拟研究了表面硬化钢的磁性能和微观结构的关系.Jr Aranas 等[11]对管道钢样品进行了维氏硬度测试,分析了不同钢管间硬度对MBN 均方根值的影响.学者还研究了材料应力状态对MBN 信号的影响.Jiles 和Suominen[12]提出了用于描述MBN 效应的磁滞模型,对材料表面压应力对MBN 信号峰值的影响进行了理论分析,理论分析得到的信号峰值随应力的变化规律和实验数据保持一致.Jagadish 等[13]通过厚壁管道实验发现当外加载荷与磁场方向相同时,压应力增大使得MBN 信号均方根值减小,拉应力增大使得MBN 信号均方根值增大.Krause 等[14]通过不同拉伸应力下MBN 测量实验分析了拉伸应力大小与方向对MBN 能量信号的影响规律.
上述研究多聚焦于材料表面的应力状态评价,学者们也针对应力状态沿厚度方向存在变化的问题开展了研究.Mierczak 等[15]基于应力与磁化关系,由非磁滞微分磁化率与应力的线性关系得到应力和MBN 信号峰值的线性表达式.Santa-aho等[16]在单轴逐步加载条件下对碳钢表面的MBN响应进行测量,分析了材料内部应力变化对MBN均方根值的影响.Desvaux 等[17]提出了一种基于MBN 信号的非破坏性残余应力分布评估方法,通过与残余应力的X 射线评估结果对比,验证了利用MBN 信号对应力分布评估的有效性.Lasaosa等[18]实验测量了沿深度方向不同应力分布情形下的MBN 信号.Kypris 等针对基于信号衰减效应对铁磁板具有恒定均布应力时的MBN 信号强度进行了理论分析[19],并针对两层复合板内具有不同残余应力的情形进行了讨论[20].
明确材料内部应力分布和检测信号之间的关系,可对基于MBN 信号的材料应力状态评估提供重要指导.本文通过考虑信号传播过程中的信号强度衰减效应,结合应力值相关的磁巴克豪森激发(magnetic Barkhausen excitation,MBE) 强度表达式,采用沿厚度方向分层的积分求解方法,获得了内部存在应力分布的铁磁板表面MBN 信号的解析解.基于已有实验结果,证实了本文模型能反映铁磁板内部均匀应力情形时MBN 信号随不同检测频率的变化规律.采用本文理论模型,研究得到了铁磁板应力分布、磁导率、电阻率、铁磁板厚度等参数对表面MBN 信号的影响规律.研究表明,基于MBE 信号强度衰减效应建立的解析分析模型,可以对应力检测的MBN 检测方法的基本实验现象和规律给出合理解释.
2 铁磁板表面MBN 信号解析模型
2.1 MBN 信号分析模型
在实际工程中,经加工强化处理得到的超高强度钢内部常存在残余应力.服役过程中,残余应力的大小及分布状态常对结构的安全性能和寿命有很大影响.本文探讨基于MBN 信号的板材残余应力检测方法,针对厚度为h(单位为m)的铁磁板,沿厚度方向存在非均匀分布的应力时,建立不同的von Mises 等效应力大小和分布状态下铁磁板表面MBN 信号的预测模型.图1 所示为铁磁板沿厚度方向存在残余应力分布时的MBN 检测示意图,铁磁板由均质且各向同性铁磁材料构成.建立如图1 所示坐标系,对矩形铁磁板进行应力检测时,在y=0 平面内进行MBN 信号检测探头的扫查检测.假设探头与铁磁板表面接触良好,MBN信号由探头附近区域的MBE 与电磁参数等决定,所以MBN 信号主要受到探头下方区域随厚度方向变化的应力分布的影响,可忽略与铁磁板表面平行的平面内应力非均匀分布的影响.
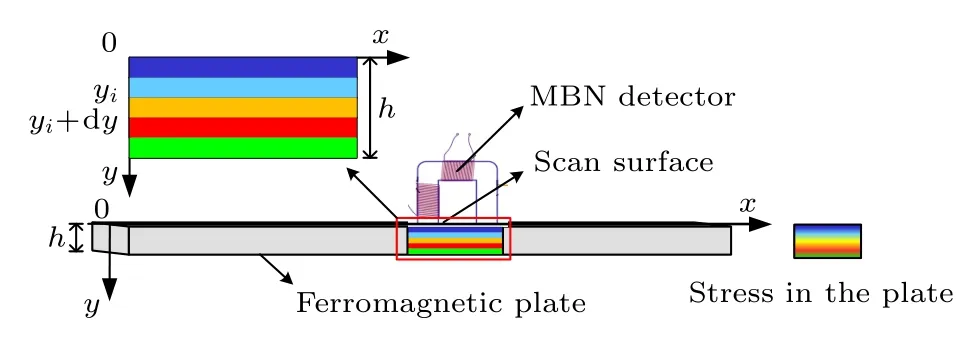
图1 铁磁板沿厚度方向应力分布诱导的MBN 信号模型图Fig.1.Model of MBN signal induced by the stress distribution along the thickness direction of a ferromagnetic plate.
受到磁化作用后的激发单元,由于磁畴运动诱导的MBN 效应,会产生不同频率的MBE.在距检测面y处取一微元 (yi,yi+dy),该激发单元产生的MBE 强度为Vorig(y,ω).由文献[19]可知,将MBE假设为白噪声,因此每个频率对应的Vorig(y,ω)具有相同的值.电磁信号是由激发位置传播到材料表面的,信号强度在这个传播过程中发生衰减.频率为ω(单位为Hz)的MBE 从激发单元传播到铁磁板表面的过程中会发生衰减,铁磁板表面产生的MBN 信号强度为[20]
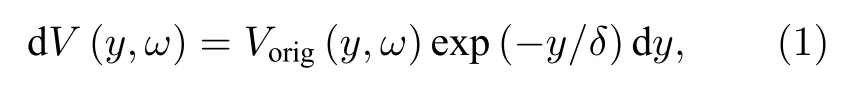
其中,dV(y,ω)为距离表面y(单位为m)深度处的频率为ω的MBE 所对应的MBN 信号强度,Vorig(y,ω)为距离表面y深度处的MBE 强度(单位为V),ω为该激发的频率(单位为Hz).
(1)式中参数δ反映信号强度衰减效应,由传播过程中信号强度衰减为1/e 时对应距离所确定[20]:

其中,ρ为材料电阻率(单位为 Ω·m),µ为材料磁导率(单位为H/m).材料磁导率满足µ=µ0µr,µ0=4π×10−7H/m 为真空磁导率,µr为材料相对磁导率,ω为信号频率(单位为Hz).
参考已有方案[20],不同频率下任意深度处的MBE 强度Vorig(y,ω) 可简化认为由该激发深度所对应的残余应力σ唯一决定.对于宽度为dy的铁磁板微元而言,可认为微元内部的应力是均匀的,等于激发深度y处的等效应力值.(1) 式可以表示为
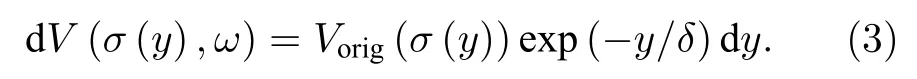
当已知不同深度y处的各个频率值ω所对应MBE 强度Vorig(σ(y)),基于(3)式,可以得到不同深度y处 MBE 在铁磁板表面所对应的MBN 信号.沿着深度y对MBN 信号进行积分,可以得到不同频率值ω所对应的MBN 检测信号.
2.2 应力相关的MBE强度模型
为确定铁磁板表面所对应的MBN 检测信号,需要首先建立不同深度y处的MBE 强度Vorig.由于Vorig受到该激发深度y处的应力状态σ所控制,本小节建立von Mises 等效应力σ在不同取值下的MBE 强度Vorig(σ)[20].
基于朗之万理论,非磁滞磁化强度Man(H)满足[21]:
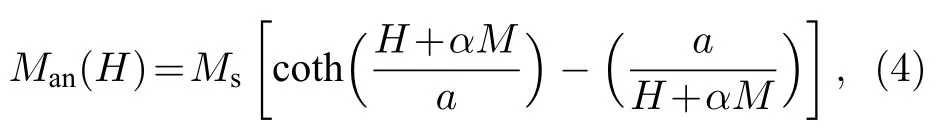
其中Ms是材料饱和磁化强度(单位为A/m),H为磁场强度(单位为A/m),α为内部磁畴间相互作用的耦合参数,a为初始磁导率决定的磁学参数(单位为A/m).
当材料内部存在应力作用时,可通过应力等效场来考虑应力状态对磁化强度影响.具体地,应力等效场Hσ和非磁滞磁化强度Man(H,σ)分别为[22,23]

其中λ是材料磁致伸缩应变,σ为该位置处的von Mises 等效应力值(单位为Pa).
由于磁致伸缩应变为磁化强度的偶函数,可以近似表示为[23]

其导数为

其中b为可实验标定的材料磁致伸缩系数.
MBN 检测中材料处于弱磁化状态,可对采用(6)式的线性简化形式进行处理[24],结合(5)式和(8)式可以得到非磁滞磁化强度Man(H,σ) 为
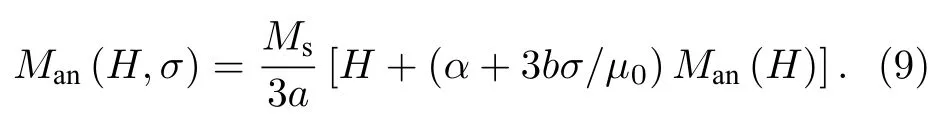
利用(9)式可以计算材料在不同外加磁场下的微分磁化率,进一步得到外加磁场为0 时的初始微分磁化率满足:
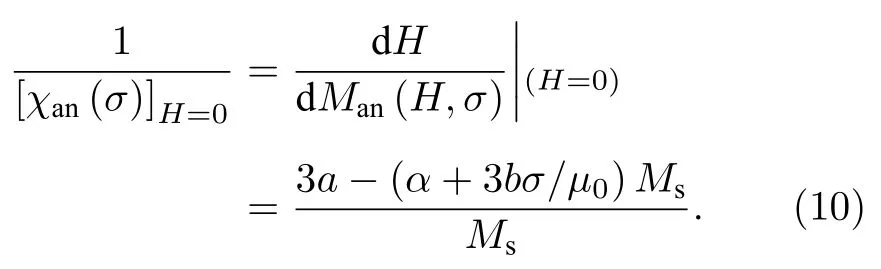
比较不同应力值下的初始微分磁化率,得到
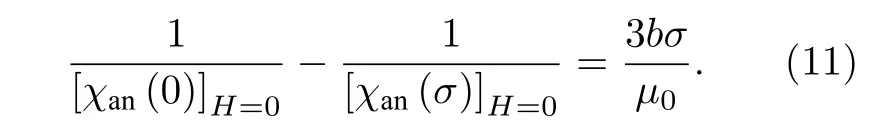
至此,确立了非磁滞情形下应力σ与初始微分磁化率之间的关系.
当材料存在磁滞效应时,最大微分磁化率常发生在矫顽点处.认为考虑磁滞效应的最大微分磁化率和非磁滞情形微分磁化率存在线性相关,即χmax≃χan.这样不同应力值下的最大微分磁化率满足如下关系:
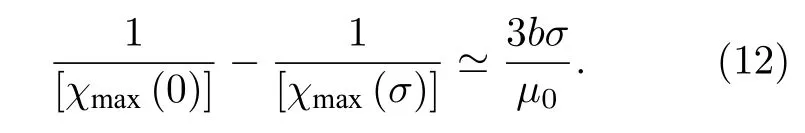
MBE 与相应位置处磁化状态正相关,假设MBE 强度与当地微分磁化率值存在线性关系,结合(12) 式,铁磁板内部MBE 强度Vorig(σ) 满足[20]:
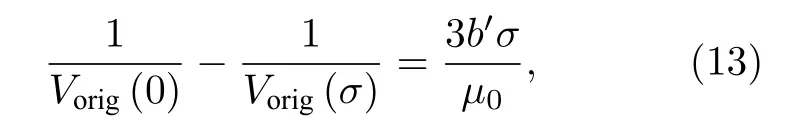
其中,b′为磁致伸缩系数b的线性修正值.
求解(13)式,得到不同应力σ值下MBE 强度Vorig(σ)的解析式:
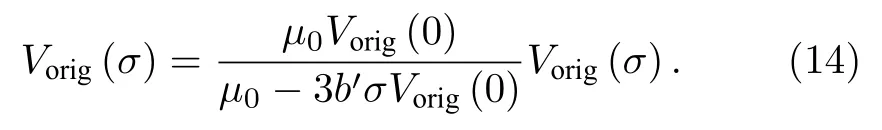
至此,已知铁磁板不同深度处的等效应力值时,可以由(14)式直接计算得到该深度处的MBE强度Vorig.
2.3 MBN 信号强度的解析模型
MBN 检测过程中,铁磁板内部任意深度处的MBE 传播到铁磁板表面,产生MBN 检测信号.铁磁板表面的MBN 检测信号强度为不同深度处MBE 所对应的信号强度的线性叠加.对(3)式在0到h的深度范围内进行积分,可得出给定频率ω下MBN 信号强度为

其中N为铁磁板沿厚度方向的分层层数,h为铁磁板厚度(单位为m),Vorig(σi) 为第i层MBE 强度(单位为V),σi为第i层的等效应力值(单位为Pa).
MBN 实际检测过程中,通常只采集和分析一定频率范围内的MBN 信号,检测信号存在频率上下限分别为ω0,ω1,单位均为Hz.对(15)式在检测频率ω∈(ω0,ω1) 范围内积分,可求得铁磁板检测中MBN 信号的总强度:

至此,已知铁磁板不同深度处的应力值时,由(15)式可以计算得到不同检测频率下的铁磁板检测中MBN 信号强度,由(16)式可直接计算得到铁磁板检测中MBN 信号总强度.
3 MBN 信号解析模型的分析与讨论
3.1 具恒定应力铁磁板问题的分析验证
针对铁磁板具有恒定应力的情形,通过与已有文献[16]实验结果进行对比,以证实本文解析模型的正确性.理论分析所采用的参数与文献[19]所采用的参数保持一致.如图2 所示,对厚度为h的矩形铁磁板进行应力检测,通过MBN 信号检测探头在铁磁板表面进行信号采集,探头与铁磁板表面接触良好,其中铁磁板内部存在恒定应力值σ.
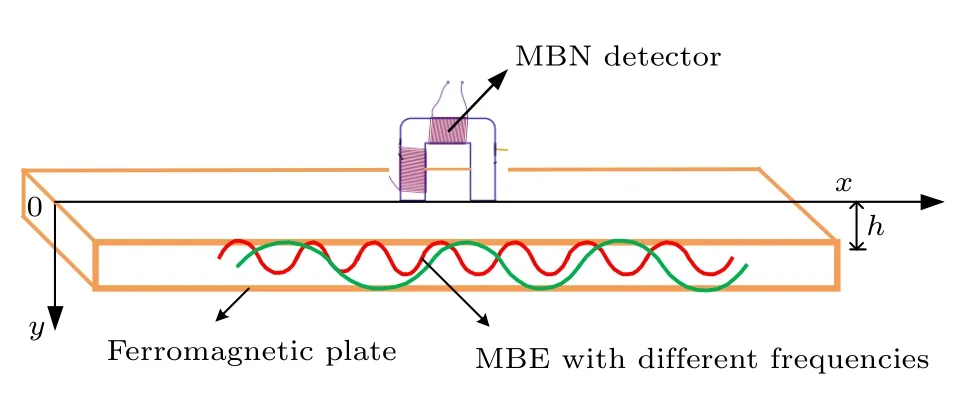
图2 铁磁板内部为恒定应力时MBN 检测Fig.2.MBN testing on the ferromagnetic plate under a constant stress.
基于本文解析(15)式和(16)式可以分析具恒定应力的铁磁板表面的MBN 信号强度和总强度.对于铁磁板内部存在恒定应力的情形[19],根据(15)式,在(16)式中取N=1,则铁磁板表面的MBN 信号强度和总强度为
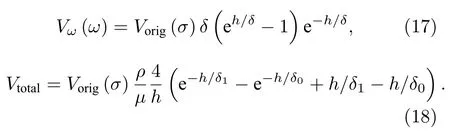
图3 给出了利用(17)式计算得到的铁磁板内为恒定应力时MBN 信号强度随着检测频率变化的理论分析结果与已有文献的实验数据的对比,对所有曲线进行了归一化处理.图3 理论分析所采用的参数为h=0.1×10−3m,µr=3000,ρ=0.6×10−7Ω·m,b′=6×10−16m2/(V·A2),铁磁板内恒定应力的取值为0 Pa 和120 MPa.从图3 可以看出,铁磁板内应力相同时,MBN 信号强度随着检测频率的增大而减小;相同检测频率的MBN 信号强度随着应力的增大而增大.本文理论模型预测的MBN 信号强度随应力和检测频率的变化规律与文献[19]报道的基本规律保持一致,证实本文解析模型的正确性.值得注意的是,文献[19,20]仅分析了单层和双层板存在恒定残余应力的巴克豪森频谱强度.本文后续的分析表明,本文模型可处理任意N层复合板或者任意形式应力分布情形的磁巴克豪森噪声检测信号.
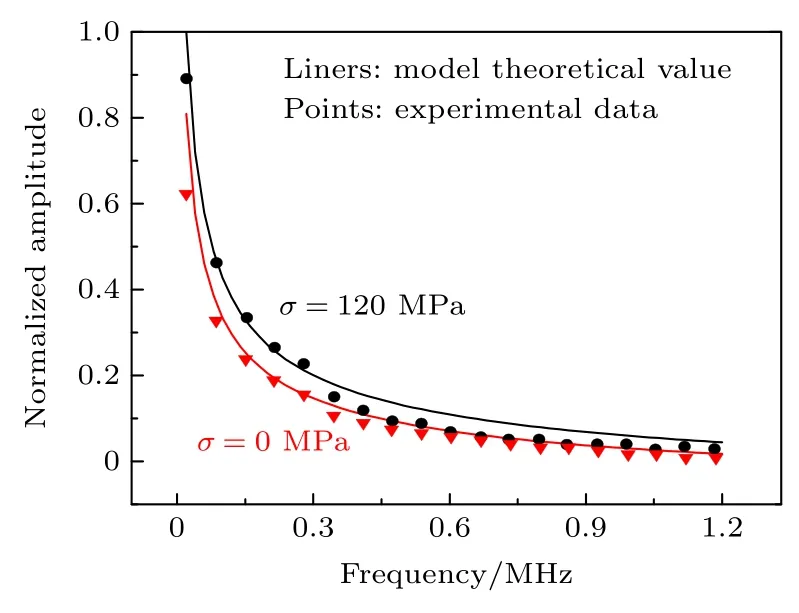
图3 不同应力下MBN 信号强度随频率变化的对比分析[19]Fig.3.Comparison of the theoretical results of MBN signal intensity versus frequency with experimental data[19].
3.2 铁磁板电磁参数对MBN 信号的影响
图4 分析了材料电阻率对铁磁板表面MBN信号强度和总强度的影响.此处假设铁磁板内应力沿厚度方向呈线性变化σ(y)=σ0+my,其中应力沿厚度方向的变化梯度m=Δσ/h,h为铁磁板的厚度(单位为m);Δσ为上下表面的残余应力差值(单位为Pa),其值为8 MPa.铁磁板表面应力σ0取值120 MPa,材料电阻率ρ取值范围为0.6×10–7—1.8×10–7Ω·m,解析求解中取分层层数N=100,检测频率上限ω1为10 kHz,检测频率下限ω0为1 kHz,模型计算所采用的其他参数与图3所采用的参数保持一致.图4(a)给出了材料电阻率参数对MBN 信号强度的影响,其中铁磁板厚度为2×10–3m.从图4(a)可以看出:电阻率ρ相同时,MBN 信号强度随着检测频率ω的增大呈现逐渐减小并趋于稳定的现象;相同检测频率的MBN信号强度随着电阻率ρ的增大逐渐增大.这种变化规律符合文献[19]报道的MBN 信号强度随频率的变化规律.图4(b)给出了铁磁板厚度h变化时,材料电阻率参数对MBN 信号总强度的影响.铁磁板厚度h为0.2×10–3—2×10–3m.从图4(b)可以看出:电阻率ρ相同时,MBN 信号总强度随着铁磁板厚度h的增大呈现逐渐增大并趋于稳定的现象;铁磁板厚度h相同时,MBN 信号总强度随着电阻率ρ增大逐渐增大,这种变化规律与信号传播过程中的强度衰减现象相吻合.
图5 进一步分析了材料磁导率参数对铁磁板表面的MBN 信号强度和总强度的影响,铁磁板电阻率ρ=0.6×10−7Ω·m,铁磁板相对磁导率µr为1000—4000,模型计算所采用的其他参数与图4 所采用的参数保持一致.图5(a)给出了频率变化时,材料磁导率对MBN 信号强度的影响,铁磁板厚度h为 2×10−3m.从图5(a)可以发现:磁导率µ相同时,MBN信号强度随着频率ω增大呈现逐渐减小并趋于稳定的现象,相同检测频率的MBN信号强度随着磁导率µ增大逐渐减小,这种变化规律符合信号传播过程中的强度衰减现象.图5(b)给出了铁磁板厚度变化时,材料磁导率参数对MBN 信号总强度的影响.从图5(b)可以发现:磁导率µ相同时,MBN 信号总强度随着铁磁板厚度h增大呈现逐渐增大并趋于稳定的现象;铁磁板厚度h相同时,MBN 信号总强度随着磁导率µ增大逐渐减小.实验发现随着磁导率减小的铁素体含量增大,MBN 信号强度增大,这反映了磁导率对MBN信号的影响[25].这与本文理论得到的MBN 信号强度随磁导率增大而减小的变化趋势保持一致.
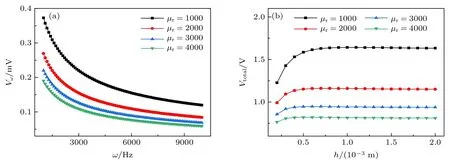
图5 磁导率对MBN 信号强度的影响 (a)信号强度与频率的关系;(b) 信号总强度与板厚的关系Fig.5.Effect of magnetic permeability on the MBN signal strength:(a) The signal intensity versus frequency;(b) the total signal intensity versus thickness of the ferromagnetic plate.
图6 进一步分析了Vorig(0) 对铁磁板表面的MBN 信号强度和总强度的影响.Vorig(0) 为铁磁板内部应力σ=0 时,铁磁板内部MBE 强度,取值如图6 所示.铁磁板电阻率ρ=0.6×10−7Ω·m,模型计算所采用的其他参数与图4 所采用的参数保持一致.图6(a)为频率变化时,Vorig(0) 对MBN信号强度的影响,铁磁板厚度h为 2×10−3m.从图6(a)可以发现:Vorig(0) 相同时,MBN 信号强度随着频率ω增大呈现逐渐减小并趋于稳定的现象,相同检测频率的MBN 信号强度随着Vorig(0) 增大逐渐增大.图6(b)为铁磁板厚度变化时,Vorig(0)参数对MBN 信号总强度的影响.从图5(b)可以发现:Vorig(0) 相同时,MBN 信号总强度随着铁磁板厚度h增大呈现逐渐增大并趋于稳定的现象;铁磁板厚度h相同时,MBN 信号总强度随着Vorig(0)增大逐渐增大.
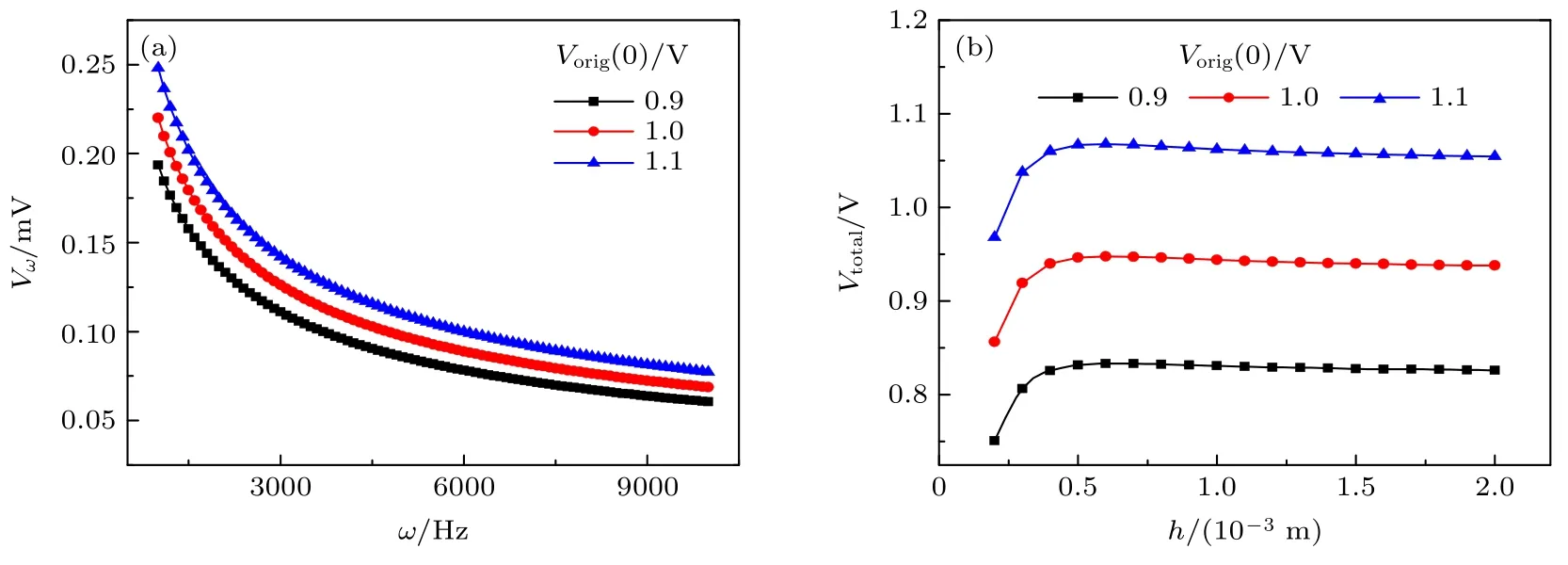
图6 Vorig(0) 对MBN 信号的影响 (a) 信号强度与频率的关系;(b) 信号总强度与板厚的关系Fig.6.Effect of Vorig(0) on the MBN signal strength:(a) The signal intensity versus frequency;(b) the total signal intensity versus the thickness of the ferromagnetic plate.
3.3 检测参数对MBN 信号的影响
图7 给出了不同铁磁板厚度条件下,检测频率上、下限值对铁磁板表面的MBN 信号总强度的影响,铁磁板厚度为0.2×10–3—2×10–3m,材料电阻率ρ=0.6×10−7Ω·m,模型计算所采用的其他参数与图4 所采用的参数保持一致.图7(a)中检测频率上限ω1取10000 Hz,检测频率下限ω0取500—1500 Hz,图7(b)中检测频率上限值ω1分别为9000—11000 Hz,检测频率下限值ω0取1000 Hz.从图7(a)和图7(b)可以看到:检测频率上下限值相同时,MBN 信号总强度随着铁磁板厚度h增大呈现逐渐增大并趋于稳定的现象;铁磁板厚度相同时,MBN 信号总强度随着频率下限值ω0的减小逐渐增大,随着频率上限值ω1的增大逐渐增大.这表明,随着检测频率范围增大,铁磁板表面的MBN信号总强度逐渐增大,这一变化规律符合实验中滤波频率对MBN 信号的影响结果[26].

图7 不同板厚下,检测频率(下、上限)对MBN 信号总强度的影响 (a) 检测频率下限;(b) 检测频率上限Fig.7.The MBN signal strength varying with thickness of the ferromagnetic plate in three cases of different (a) the low and (b) upper limits of the detection frequency.
3.4 应力分布对MBN 信号的影响
图8 分析了铁磁板内部沿厚度变化的应力分布对铁磁板表面的MBN 信号总强度的影响.分析中取铁磁板上下表面残余应力均为σ0=200×106Pa,当应力σ(y) 沿深度方向呈抛物线关系时,满足σ=σ0+4Δσ(y2−hy)/h2,其中h表示铁磁板的厚度,Δσ反映表面铁磁板表面的残余应力σ0与铁磁板h/2 厚度处应力值的差异.图8(a)给出铁磁板厚度为 1×10−3m 时,材料内部应力沿厚度方向变化.可以看出,随着 Δσ的增大,铁磁板表面的残余应力σ0与铁磁板h/2 厚度处应力值的差异增大,应力沿着深度方向的非线性变化程度更显著.图8(b)分析了 Δσ取不同值时的应力分布对MBN信号总强度的影响,铁磁板厚度h为0.2×10–3—2×10–3m,材料电阻率ρ=0.6×10−7Ω·m,模型计算所采用的其他参数与图4 所采用的参数保持一致.由图8(b)可以看到:Δσ相同时,MBN 信号总强度随着铁磁板厚度的增大逐渐增大并趋于稳定;铁磁板厚度相同时,随着 Δσ增大MBN 信号总强度逐渐减小.
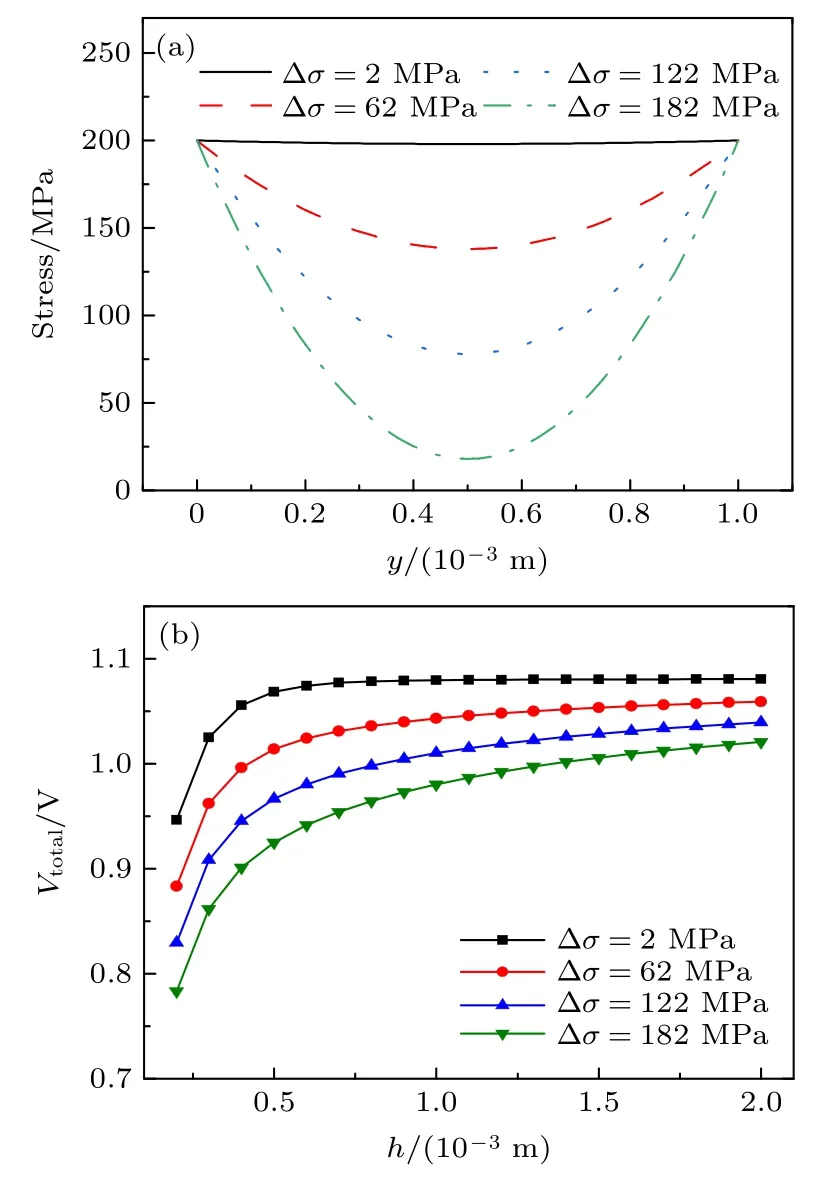
图8 不同应力分布情形下的MBN 信号总强度 (a) 沿板厚度方向的应力分布;(b)不同应力分布下MBN 信号总强度随板厚的变化Fig.8.Total MBN signal strength under the different stress distribution along the thickness of the ferromagnetic plate:(a) Four different stress distributions along thickness direction of the plate;(b) the total signal intensity versus thickness in these four cases.
在实际应用中,铁磁板内部存在着复杂的应力分布.本文采用沿厚度方向的分层模型实现MBN 信号强度的解析求解,图9 讨论了不同材料电阻率和材料磁导率条件下,分层层数N对铁磁板表面的MBN 信号总强度的影响.图9 计算中所采用的参数为,铁磁板厚为 1×10−3m,ΔVtotal=反映了取相邻分层层数时MBN 信号总强度的差异,为将铁磁板分为N层时铁磁板表面的MBN 信号总强度,模型计算所采用的其他参数与图4 所采用的参数保持一致.图9(a)中µr=3000 ,图9(b)中ρ=0.6×10−7Ω·m,所采用的其他参数如图中所示.由图9(a)和图9(b)可以看出:不同的材料磁导率和电阻率参数取值,ΔVtotal值随着分层层数的增大呈现减小并在层数大于8 层后逐渐趋于稳定.这是因为,随着分层层数的增大,各层内的应力差异减小,这样各层采用均匀应力的解析表达式进行MBN 信号总强度计算时的误差也随之减小.本算例分析证实了采用沿厚度方向的分层模型实现MBN 信号强度的解析求解是可行的.
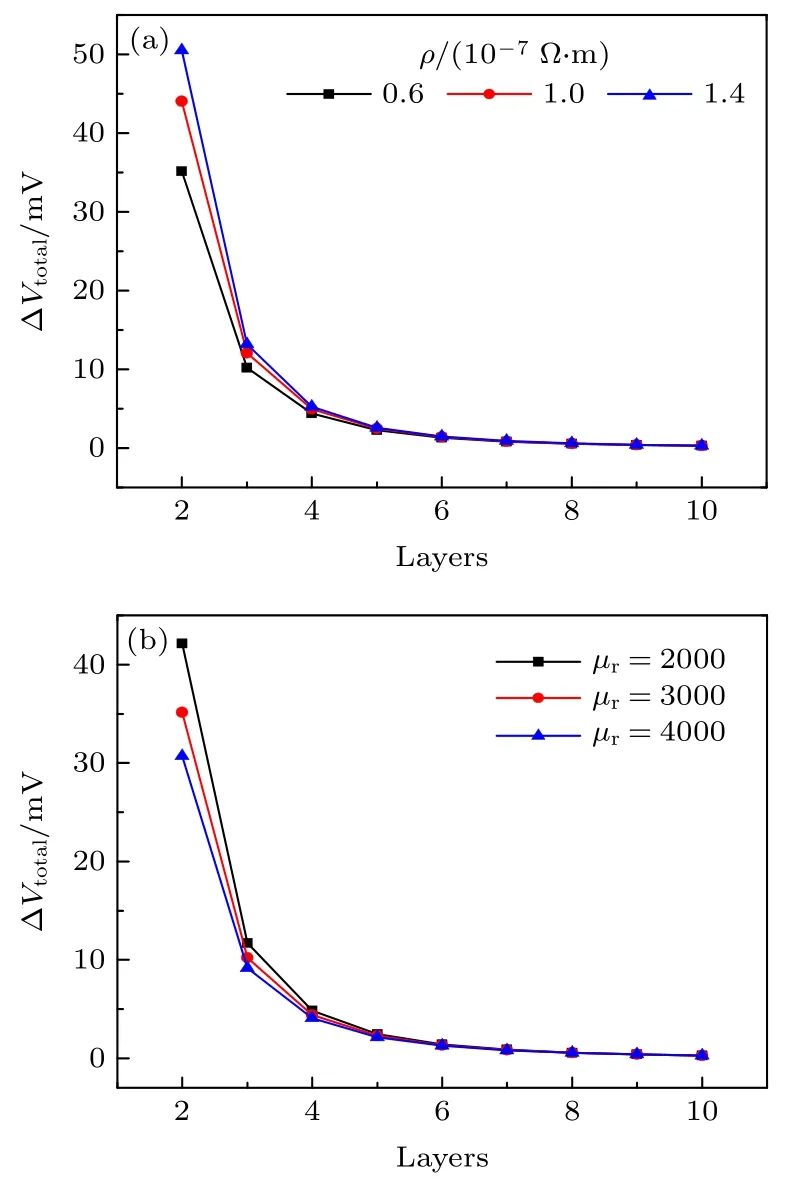
图9 分层层数对 ΔVtotal 的影响 (a) 材料电阻率不同;(b) 磁导率不同Fig.9.Calculated ΔVtotal varying with the number of layers along thickness direction of the ferromagnetic plate:(a)Different electrical resistivities;(b) different magnetic permeabilities.
4 结论
本文针对铁磁板,推导了与von Mises 等效应力值相关的磁巴克豪森信号强度表达式,根据磁巴克豪森信号传播过程中的强度衰减效应,沿厚度方向进行分层分析,建立了铁磁板表面MBN 信号的解析预测模型.基于已有实验结果,证实本文模型能反映不同检测频率下铁磁板内部均匀应力值差异对信号的影响规律.而且,对于铁磁板内存在应力分布的情形,采用本文解析模型,研究得到了铁磁板内应力分布,铁磁板的磁导率、电阻率和厚度等参数对铁磁板表面磁巴克豪森信号的影响规律.
本文解析理论模型,不仅可对应力检测的磁检测方法的基本实验现象和规律给予合理解释,同时也为发展磁巴克豪森无损检测技术提供了一定的理论依据.需要指出的是,本文理论中仅研究了von Mises 等效应力相关的磁巴克豪森激发模型,而工程实际中铁磁构件面临更为复杂的工况,内部应力比较复杂,同时还有可能发生塑性变形累积等.后续持续开展深入的磁巴克豪森激发理论研究,这无论对磁无损检测理论还是相关工程实际应用,都是非常必要的.当前的研究存在一些假设和简化,限制了模型针对实际检测的应用能力.作者希望在未来研究中,从三维空间非均匀分布残余应力情形,模型中等效磁导率假设忽略了应力应变状态的影响,以及弹塑耦合、温度等复杂因素的影响规律等方面进行模型完善和拓展,以使其能够应用于实际检测中的复杂工况.

