一种基于遗传算法的试题推荐方法
徐明远
(上海工程技术大学电子电气工程学院,上海 201600)
0 引言
如今已进入大数据时代,智能教育、在线教育发展十分迅速,其可较为便利地为学生提供所需的试题进行练习,从而协助学生对学过的知识进行巩固。但是,考虑到试题资源数量庞大,学生很难在有限时间内对全部试题都进行练习。因此,如何协助学生在海量的试题资源里找出最合适的试题,是一个非常关键的问题[1]。近年来,学者们尝试将推荐系统相关技术应用于试题推荐等领域。如果使用传统推荐系统在电子商务方面的应用案例进行类比,则可将学生当作电子商务中的客户,将试题当作商品,学生考分当作客户对商品的评分。因此,如果需要预估学生的试题得分,使用试题推荐的方式比较简洁、容易理解,且能够获得较好效果[2]。
通过分析传统推荐系统可发现,基于协同过滤的算法是运用最广泛的一种算法,其分成两个类别[3]:一是以近邻为基础的协同过滤法,该方法主要通过参照学生的历史答题情况,求出不同学生之间的近似度,由此找出最为近似的学生,然后根据近似学生的得分情况预估目标学生的得分,最终参照预测的得分数据进行相应的试题推荐工作;二是以遗传算法模型为基础的协同过滤。该方法通过矩阵分解方式对学生与试题进行相应分解,形成一组有关隐藏因子的影响因素,由此构建关于学生与试题二者关系的低维矩阵,并展示出二者在低维空间内的表现情况,从而预估学生的试题分值,最后参照预估分值实施对应的试题推荐工作。
认知诊断理论作为教育与心理测量学科中新一代测量理论的核心,主要通过认知诊断模型对被试的作答数据进行分析研究,发掘学生潜在、不可直接观察的知识状态与作答反应模式之间的联系,为表达学生的知识状态带来便利[4]。
将认知诊断方法与遗传算法相结合应用于试题推荐领域,既能很好地解释算法的合理性,又能提高试题推荐的准确性,在在线学习越来越普遍的今天,提供了试题推荐的一种优化方案。
1 相关研究
为准确诊断学生的知识状态,研究者们对认知诊断模型进行了深入研究。如文献[5]提出规则空间模型,通过转换被试对试题的反应模式,得到其试题掌握情况与知识状态,该方法具有较高准确性,但由于专家标定具有主观性,应用范围较为局限;文献[6]提出先确定属性层级关系,再对学生知识状态进行诊断的属性层级模型,进一步提高了认知诊断模型的准确性,但该诊断方式仍具有一些误差。本文采用的DINA 认知诊断模型在考虑属性层级关系的前提下,加入被试作答试题时猜测与失误的概率,相比其他模型能更准确地诊断被试的知识结构。
结合认知诊断模型,根据学生的知识结构进行试题推荐,使推荐更具有合理性,是当下的研究热点。文献[7]通过获取学生的学习方式、知识状态和学习方法等信息,提出一种个性化试题推荐方法;文献[8]结合使用多级属性评分认知诊断模型和遗传算法模型,根据学生信息进行动态试题推荐。本文将DINA 模型诊断出的知识状态作为试题推荐的先验知识,从知识结构的角度进行分析,结合隐含语义分析(LSA)对试题数据进行处理,结果表明,使用遗传算法得到的试题推荐结果相比传统方法更加准确。
2 认知诊断
2.1 认知诊断理论研究
从认知心理学方面进行分析,认知诊断模型能够更好地从知识点这个层级针对学生的认知形态创建相关模型,并辅助学生进行高效的学习规划。目前的认知诊断模型非常多,主要从两个层面对其进行分类:①对于认知诊断模型而言,可分成离散型、连续型;②对于认知诊断方法而言,可分成一维技能、多维技能[9]。在很多认知诊断模型中,使用最普遍的是有关一维连续认知建模的项目反应理论(IRT)模型,以及关于多维离散认知建模的DINA模型[10]。
其中,IRT 只是根据学生的答题状况对学生实施建模,从而得到一维连续能力值,并通过相关能力值展示出学生的综合实力。IRT 模型将学生设计为一个具备单一能力值的对象,然而在现实应用过程中,考虑到不同试题考察的知识范畴不同,容易导致模型无法体现学生在不同知识方面的实力差距。对于这些情况,有些学者提出了补偿性多维IRT模型MIRT-C[11],以及非补偿性多维IRT模型MIRT-NC,通过这些模型能够从多个方面针对学生实力进行建模操作[12]。
关于受推荐试题对于学生真实难度的问题,本文通过准确作答率指标SR 进行相应评测,设置难度区间后,学生认真作答了全部推荐试题,之后求出准确作答的比例。分母为推荐试题总数,分子为学生正确作答的推荐试题数量,即:

2.2 评价方法
聚类分析是一种无监督的学习方式,如何对聚类结果进行客观、公正的评价,是聚类问题中最关键的研究内容之一[13]。常用的聚类结果评价方法较多,包括外部评价法与内部评价法,这两种评价法都是以统计测试为基础,在运算复杂性较高时,以聚类质量指数衡量数据集与已知架构的匹配度。另外还包括相对评价法,在数据集分类结构未知时可采用这种评价法。该评价法其实是找出一个聚类算法,并且确保在相应的假定与参数条件下可定义的最佳聚类结果。
本文采用外部评价法对试题数据进行处理,以一类提前指定的架构为基础,这类架构能够体现出人们对数据集聚类架构最直观的认知,并且所有数据项的分类均处于已知状态[14]。常见的外部评价方法有熵(Entropy)方法、特征测量(F-measure)等。
(1)熵。将聚类结果设定成CS(Clustering Solution),聚簇j 属于分类i 的概率为Pij。聚簇指聚类算法得到的类簇,分类指原始数据集中数据的分类。聚簇j的熵定义为:
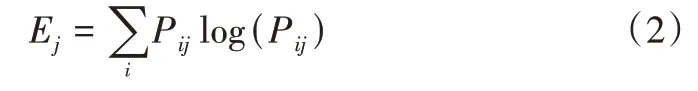
聚类结果的总熵可定义为各个聚簇熵的加权和,即:

其中,nj代表聚簇j的大小,k 代表聚簇数量,n代表全部对象数量。
对于最佳的聚类结果而言,聚簇内所有试题均源自于单独一个分类,此刻熵是0。如果熵值较小,则聚类结果通常较好。
(2)特征测量。特征测量的优劣主要与查准率(Precision)、查全率(Recall)两个参数相关。对于聚类i和分类j,分类j的F(F-measure)值定义如下:
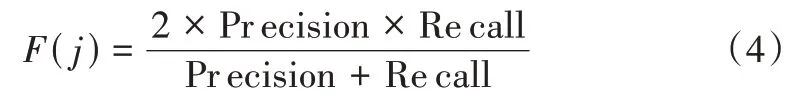
假定{relevant}代表与分类j有关的试题集合,{retrieved}代表聚类i内全部试题集合,{relevant}∩{retrieved}代表聚类i中属于分类j的试题集合,查准率、查全率依次根据以下方法获取:
查准率(Precision):聚类i中属于分类j的试题数量与聚类i中所有试题数量的比值。
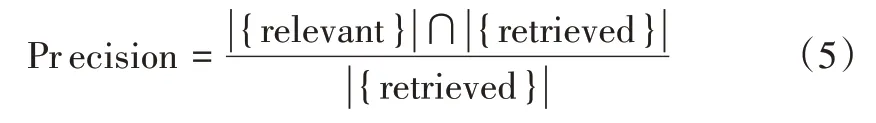
查全率(recall):聚类i中属于分类j的试题数量与分类j中全部试题数量的比值。
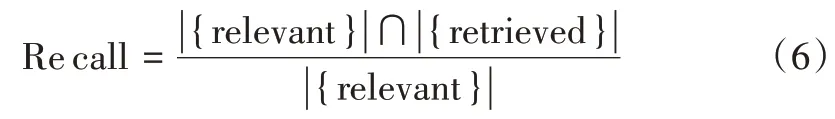
所有对象的特征测量为所有分类F值的平均值:
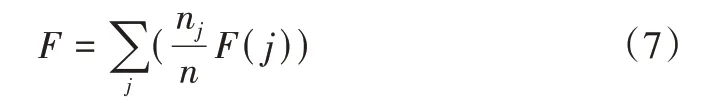
其中,n为试题数目。由特征测量的定义可知,F-measure值越大,聚类效果越好。
3 基于遗传算法的聚类集成
3.1 遗传算法
遗传算法(Genetic Algorithms,GA)能够对生物进化规律进行模拟,属于一类随机化的搜寻方式,其对于架构化的对象直接实施操控,具备内在并行性,并且具备全局寻优的能力;能够选用概率化的寻优方式,可通过自动方式获得相应的搜寻空间并实施相应的引导优化,通过自适应方式调节搜寻方向[15-16]。其首先通过编码,采用字符串表达实际问题,这种字符串相当于遗传学中的染色体(Chromosome),从而将解空间的解数据转换成遗传算法可处理的遗传空间的基因型串结构数据,其中字符串的每一位称为基因位,每个字符串都是问题的一个解(不一定是最优解),每一代所产生的字符串个体集合称为种群(Population);然后利用选择(Selection)、交叉(Crossover)、变异(Mutation)等操作,使优者繁殖、劣者淘汰,一代一代重复操作,最终找到最优解[17]。
遗传算法基础流程如下:
Step1:选取相应的编码样式,设置好交叉率、突变率等参数,并设置进化代数Gen=0。
Step2:对种群实施初始化操作,从而获取P(Gen)。
Step3:参照目标函数求出种群内所有染色体的适应度。
Step4:Gen=Gen+1。
Step5:假如Gen 值能够符合设置的相关要求,则转至Step11,否则转至Step6。
Step6:从P(Gen-1)中找出两个成员,其中选定的概率及染色体适应度呈正比例关系。
Step7:根据提前设置好的杂交率,从所有选定染色体的一个随机点上实施对应的杂交处理。
Step8:根据提前设置好的变异率,从所有选定染色体上随机确认一个点,并转变对应的位值。
Step9:选定变异后的个体与P(Gen-1)群体内具有较大适应度的染色体,构成种群P(Gen)。
Step10:转至Step3。
Step11:导出种群P(Gen)内具有最大适应度的个体,并终止算法。
3.2 基于遗传算法的聚类集成方法
对于基于遗传算法的聚类集成方法(CEGA)而言,其基础思想为:对于数据集实施H 次聚类算法[18](如Kmeans),从而形成H个聚类成员Π={π1,π2,...,πH},之后,由于基聚类获取的聚类成员仍存在一定错误,因此能够对聚类成员进行相应的量化处理,得到:

在聚类成员集成阶段,将Π={π1,π2,...,πH}作为遗传算法的初始种群,参照遗传算法的相关流程实施相应的进化处置,将获得的最优染色体作为最终聚类结果[19]。
CEGA 算法流程可参见图1。
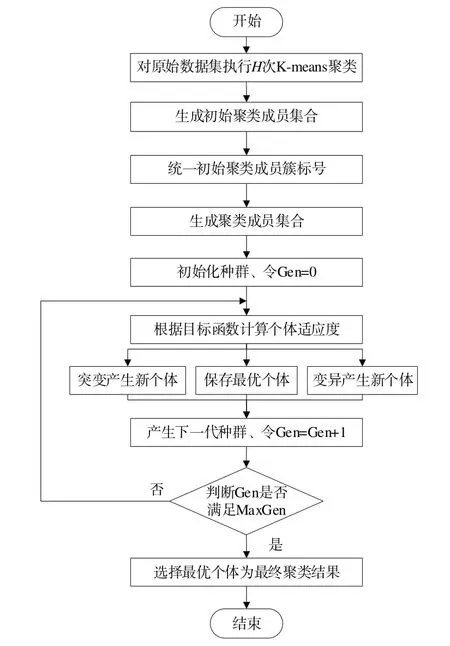
Fig.1 CEGA algorithm flow图1 CEGA算法流程
3.3 聚类成员生成
在该环节可选用经常使用的K-means 算法生成相应的聚类成员,对于初始数据集D={d1,d2,...,dn}实施H 次聚类(将参数设定成k),从而获取相应的聚类成员集合Π′=Π′为H×n二维数组,其中:

3.4 聚类成员集成
3.4.1 染色体编码
聚类成员集合选用实数编码样式进行编码操作,对于实数编码而言,其能够提高编码精度,降低运算复杂度。一条染色体对应一个聚类成员,染色体基因对应聚类成员的簇标号。很明显,在初始数据集内,数据对象数目就是染色体长度。公式(11)即代表一条染色体:

其中,为统一后的簇标号,表示在第i个聚类成员中的第j个数据对象被划分到簇中。
3.4.2 目标函数
遗传算法中最关键的是目标函数,其能够指引群体进化方向,确保染色体朝着便于问题妥善处理的方向发展。求聚类问题的解就是要找出一个聚类结果,确保接近的数据被分在同一簇中,不同数据则分在差别的簇中。采用有关聚类结果的综合评价指数(OCQ)求出任意一条染色体的聚类效果,并且传回一个适应度。
3.4.3 杂交函数及突变函数设定
在相关进化流程内,算法时常能够收敛至局部最佳点,却无法实现全局最佳,因此需要增添与进化代数关联的交叉率、突变率等参数,以提升算法在全局方面的搜索实力。
杂交函数相关定义如式(12)所示。

其中,Pctemp=为设置的最大交叉率,Pcmin为设置的最小交叉率,应当保证交叉率在最大与最小值区间内进行改变。
突变函数相关定义如式(13)所示。

4 试题推荐分析
4.1 隐含语义分析
隐含语义分析(Latent Semantic Analysis,LSA)是一类科学、合理的降维方式,可实现迅速降维,同时凸显出文本之间的语义关系[22]。
尽管LSA 是用试题中包含的词表示试题语义,能够最大限度掩盖试题的语义架构,但考虑到试题内关于用词的多元化特性,LSA 经过奇异值分解及取k 秩近似矩阵后,不但能减少原词条试题矩阵内涵盖的噪声,从而更好地凸现词条与试题间的语义关联,而且能减小试题词条的向量空间,从而降低运算复杂度,提升检索工作效率[23]。对于文本词条矩阵Wn×m,则是参照矩阵奇异值分解相关理论,将W 分解成3个矩阵的乘积:
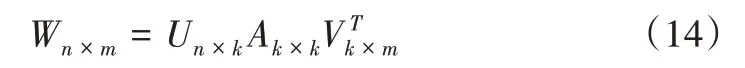
其中,U、V、A 分别代表矩阵n×k、m×k、k×k,k 代表矩阵W 的秩,其属于1 个对角矩阵。至于对角线元素,则是矩阵W 的k个奇异值依据递减次序进行相应排布。
假如在矩阵A 内仅选取前面r 个最大的矩阵,则能获取相应的对角矩阵Ar。相应地,如果选定U、V 最前面的r列,则能获取Ur、Vr。参照这3 个矩阵组建得到r-秩矩阵Wr,如图2所示。
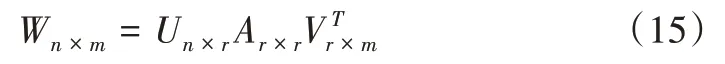
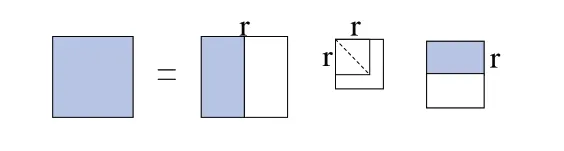
Fig.2 Constructing r-Rank matrix of W图2 构建W的r-秩矩阵
Wr是W 的r 秩近似矩阵,Ur与Vr列向量属于正交向量,依次代表文本向量、词向量,通过Wr近似代表文本词条矩阵W 以完成降维操作。在完成降维处理的空间里,对象之间则是通过词条的全局应用样式进行关联。
4.2 基于遗传算法的文本聚类集成算法模型
CEGA 作为一种高效的聚类集成算法,可结合LSA 应用于文本聚类中,形成一种新的基于遗传算法的文本聚类集成方法TCEGA(Test Clustering Ensemble Model Based on Genetic Algorithm)。该方法首先通过LSA 对文本特征矩阵进行降维处理,然后用CEGA 对降维后的矩阵进行聚类操作。整个算法过程简单、高效。TCEGA 具体步骤如下:
Step1:对于文本进行相关的预处置,并提取词频特征矩阵,通过向量空间模型展示出相关文本特征。
Step2:对词频特征矩阵进行相应转换,从而形成TF.IDF,并且进行对应的规范化处置。
Step3:运用LSA 理论对文本特征矩阵作降维处理,得到降维后的矩阵D。
Step4:对矩阵D 执行CEGA 算法。
Step5:输出最优染色体作为聚类结果。
4.3 实验结果与分析
4.3.1 实验数据与评价标准
实验数据由5 类试题库数据组成,每个试题库数据为2722维,采用平均准确率作为实验评价标准。
4.3.2 实验结果与分析
在第一组实验中,在原始文本特征矩阵数据上运行21次LSA 降维算法,每次降维程度不同,得到21 个不同维数的降维后的数据矩阵。在相同的软件与硬件条件下,在这些数据矩阵及原始数据矩阵上分别运行TCEGA 聚类算法,记录算法运行时间与聚类结果的平均准确率,根据记录的数据验证LSA 对聚类结果平均准确率及聚类速率的影响。表1 给出了不同数据维数情况下TCEGA 的运行时间与聚类结果平均准确率。
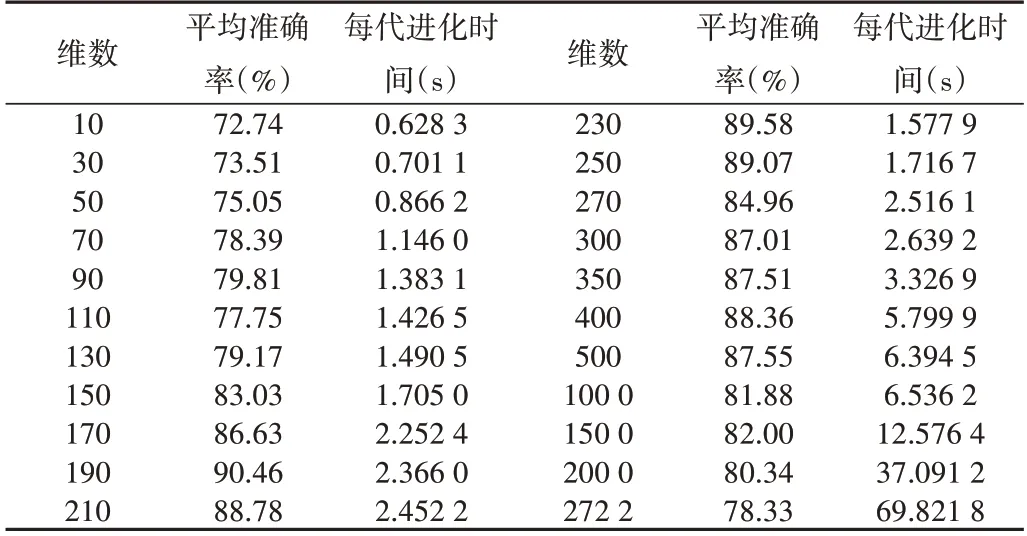
Table 1 Relationship among data dimension,algorithm running time and clustering results表1 数据维数与算法运行时间及聚类结果的关系
图3 显示了平均准确率与数据维数的关系,x 轴代表文本特征矩阵维数,y 轴代表TCEGA 聚类结果的平均准确率。图4 显示了TCEGA 平均运行时间与文本特征矩阵维数的关系,x 轴代表文本特征矩阵维数,y 轴代表算法每代平均进化时间(单位:s)。
在第二组实验中,为验证TCEGA 文本聚类方法的高效性,将常用的聚类算法如K-means、SOM 与TCEGA 作对比实验。首先用LSA 将文本特征矩阵由2 722 维降到191维,然后采用K-means 算法、SOM 与TCEGA 分别对降维后的数据矩阵进行聚类操作,并选用平均准确率作为聚类结果评价标准。
表2 给出了标准K-means 算法、SOM 与TCEGA 聚类结果的平均准确率。
实验结果表明,TCEGA 比K-means 与SOM 可获得更好的聚类结果,通过集成方法达到了提高聚类性能的目的。
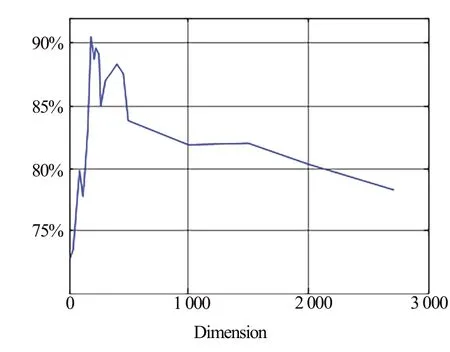
Fig.3 Relationship between average accuracy and data dimension图3 平均准确率与数据维数的关系
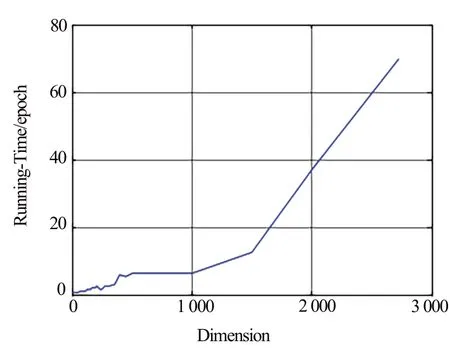
Fig.4 Relationship between average evolution time per generation and data dimension of TCEGA图4 TCEGA每代平均进化时间与数据维数的关系

Table 2 Average accuracy of clustering results of each algorithm表2 各算法聚类结果平均准确率
学生知识点掌握程度示例如图5 所示。由图可知,在DINA 模型中对学生的知识状态进行诊断,被试A 对S1、S4、S6等知识点的掌握情况较好,对S3、S8等知识点的掌握情况较差;被试B 则是对S2、S7等知识点的掌握情况较好,对S1、S5等知识点的掌握情况较差。
将被试知识点掌握程度作为算法模型的先验知识参与试题推荐,从隐含语义分析的角度对试题中的信息进行筛选,并采用TCEGA 算法实现试题选取与推荐。
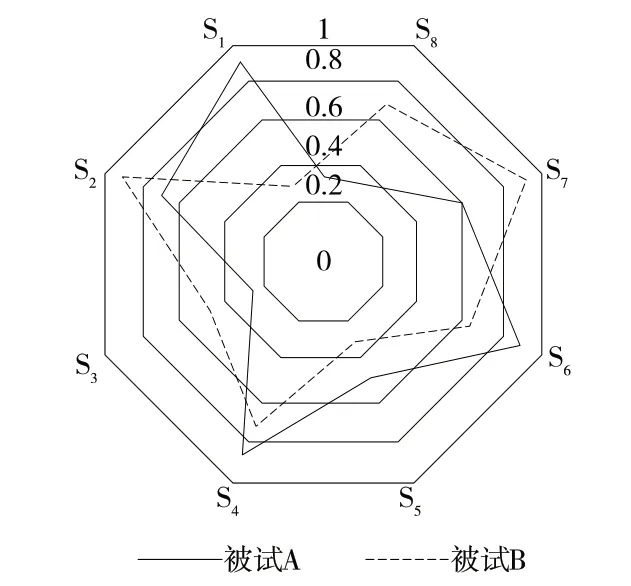
Fig.5 Examples of students'mastery of knowledge points图5 学生知识点掌握程度示例
本文提出个性化试题推荐的方式,如果推荐的试题难度较大,则根据所有学生的个性化学习情况为其推荐对应的试题,对于试题的推荐结果会具备更好的可解释性。
5 结语
本文通过对认知诊断模型与遗传算法的深入研究,提出一种基于遗传算法的个性化试题推荐方法。该方法结合学生的知识结构与试题的文本集成信息进行预测,在使用遗传算法进行试题推荐时,既考虑了群组学生在学习方面相近的情形,又改善了遗传算法个性化程度不高的问题。最终实验结果表明,在使用DINA 模型诊断出学生的知识掌握程度后,TCEGA 算法的试题推荐准确性优于传统推荐算法。
虽然本文通过结合认知诊断模型与遗传算法的方式增强了试题推荐的可解释性,提高了试题推荐的准确性,有助于在线学习模式的推广与应用,但将TCEGA 方法广泛应用于在线学习领域仍需进一步深入研究与探索。是否可引入更多学生与试题信息作为先验知识以提高算法准确性,是否可在不同学习场景应用该推荐方法,更有针对性地实现个性化在线学习与测评,将是后续研究重点。

