活塞式水平弹射装置内弹道性能研究①

陈 哲，郭 翔，余 瑞，余 剑，王志昊，吴 敏，邓康清，庞爱民,2

(1.湖北航天化学技术研究所，襄阳 441003；2.应急救生与安全防护湖北省重点实验室，襄阳 441003)

0 引言

燃气弹射是依靠火药燃烧产生高温高压的气体作为动力源的发射方式，凭借其能量密度高、响应速度快、可靠性高、环境适应性好等优点，被大量应用于各类导弹的发射过程中。水平弹射是适用于空基发射平台的发射方式，可用于攻击敌方防空单元、指挥车、各种主战坦克和装甲车辆等高价值目标，可以有效避免导弹发动机尾焰的影响，保证载机发射导弹时的飞行安全，导弹本身也不再穿越载机形成的头部激波，有利于保持导弹的姿态稳定性，提高导弹姿态的控制精度。与筒式弹射不同，活塞气缸式弹射中，火药与导弹分开放置，发射过程中产生的燃气不与导弹直接接触。因此，不需要隔热装置，有利于改善武器系统的机动性，提高隐蔽性。

弹射过程中涉及到多种载荷相互作用，不易得到其解析解，大多采用简易工程算法和数值计算方法来进行估算。谭大成详细分析了弹射过程中的内弹道特性，并建立了零维内弹道模型，给出了计算和分析的方法。李化等分析了发射过程的高、低压室内弹道方程，并基于Simulink建立了内弹道仿真计算模型，为较复杂的高、低压室内弹道计算提供了一种相对简便可靠的途径。杨文等以零维内弹道为基础，根据小型弹体发射系统相关参数与内弹道性能预估结果，提出了三种降低弹射过载的方法，并验证了降压方案的可靠性。针对活塞式弹射装置，国内外针对不同的结构也开展过大量研究。谢伟等基于零维内弹道的理论和Craige-Bampton的方法，构建了活塞式弹射发射耦合仿真平台，有利于提高仿真计算精度。唐垚等提出了多级活塞缸式燃气弹射装置，并对其进行仿真计算，该装置有利于减小导弹所受过载和出筒速度，便于合理利用空间。WANG等基于零维假设建立了考虑泄漏率的燃气无杆气缸弹射装置的内弹道模型，该装置不仅可以增加弹射行程，并提高最大弹射速度，还能防止烧蚀。目前，对水平弹射的研究相对较少，开展水平弹射研究有利于提高空基发射平台的发射能力。弹射过程的点火阶段实际情况复杂，相应理论还不完善，对于较大型弹射发射过程的影响不大，在计算时通常忽略，但小型弹射器的弹射时间短，过载相对较低，点火压强对整个内弹道计算结果的影响相对较大，在计算时应考虑。

本文以某活塞式水平弹射装置为研究对象，以零维理论为基础建立了其内弹道模型，对高压室和低压室的性能进行了预估计算。弹射过程持续时间较短，点火压强对内弹道计算结果的影响较大，建立了引燃药柱的燃烧模型，并对内弹道仿真计算程序进行了优化，使得仿真计算结果与试验结果误差较小，验证了弹射方案的可行性及内弹道预估的可靠性，为弹射装置的后续优化设计提供了理论依据。

1 弹射装置及工作原理

弹射装置为燃气作动筒式结构，燃气作动筒结构主要有两种：一种是将火药放在作动筒内燃烧，产生的高温高压燃气直接推动活塞运动，进而带动负载做功；另一种是将火药放在高压室内燃烧，燃气通过高压室尾部的喷管流出，进而推动活塞做功。前者结构简单紧凑，内弹道计算方便，但火药的燃烧与环境的压强耦合，会造成工作过程的不稳定现象。后者采用高压室喷管作动筒式结构方案，药柱在燃气发生器中燃烧，高压室建立起稳定的压强，保证了药柱的稳定燃烧，提高了工作过程的稳定性。

本文所采用弹射发射系统主要由燃气发生器(高压室)、作动筒(低压室)、活塞杆等组成，其结构如图1所示。

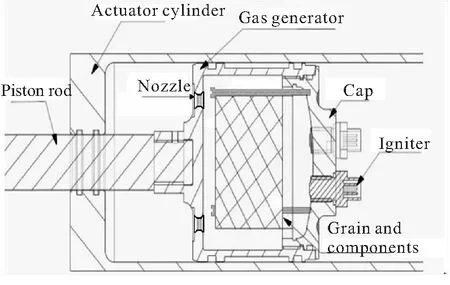
图1 弹射装置结构示意图

燃气发生器外表面与作动筒活塞缸内表面配合，起到活塞的作用，同时具有两道密封措施，保证工作时燃气流密封，发生器端盖装有点火器，底部与作动筒活塞杆螺纹连接。

燃气发生器通电点火后，引起高压燃烧室内的药柱燃烧，产生的高温、高压的燃气通过高压室底部喷管流入左端低压室，低压室处于密闭状态，随着高温、高压燃气的进入，低压室的压力升高，在气体的膨胀作用下，燃气发生器作为活塞在作动筒内向右运动，并通过底部连接的活塞杆间接带动导弹运动，使导弹离开发射筒，随着燃气发生器的加速运动，低压室容积增大，当燃气发生器达到最大行程后，作动筒内的压强逐渐减小并趋于平缓。

弹射系统必须满足相关的性能要求和结构、可靠性、安全性等要求。燃气发生器端盖与筒体之间为螺纹连接，药柱及支架通过螺钉固定在端盖上，其整体直径约为55 mm，高度约为60 mm，系统的其他主要参数和预期目标见表1。

2 内弹道数学模型

为使所设计的弹射发射系统满足相关技术要求，需要对燃气发生器和低压室的内弹道性能分析计算。根据经典内弹道方程组，采取零维内弹道模型，初步估算燃气发生器和低压室内压强的变化。

表1 弹射系统主要参数和预期目标

2.1 高压室内弹道数学模型

高压室压强变化规律直接影响到流入到低压室的燃气量，最终影响导弹在弹射装置中的运动规律。高压室工作过程和现象比较复杂，需要做出合理假设来简化计算：(1)假设燃气在高压室内是均匀分布的；(2)假设燃气在喷管中为一维等熵流动；(3)假设燃气的成分、物理化学性质固定不变；(4)假设火药燃烧过程是绝热的。参考文献[5]，可得到高压室内弹道数学模型如下：

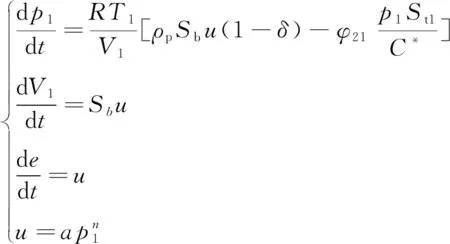
(1)

式中为某瞬时高压室燃气压强；为高压室自由容积；为火药燃气的气体常数；为高压室温度；为装药密度；为装药燃烧面积，=()，燃面变化规律与所设计的药型和包覆层相关；为燃速，=[1+(-)] ，、为初温、所对应的燃速，为温度敏感系数；为高压室喷管的流量修正系数；为高压室喷管喉部面积；为特征速度；为肉厚；为火药的燃速系数。初始状态时，燃气发生器内部压强为0.1 MPa，温度为5 ℃，自由容积为2.49×10mm。

2.2 低压室内弹道数学模型

低压室是形成弹射力的密闭空间，决定了导弹运动的速度和加速度，结合文献[12]，并根据理想气体定律、导弹运动规律等建立低压室内弹道方程组。

从高压室流入低压室的燃气流量为

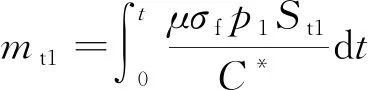
(2)

式中为总压系数与流量系数乘积。

弹射工作过程中，低压室内含有燃气和空气，结合理想气体状态方程，可以得到低压室平均压强计算方程：

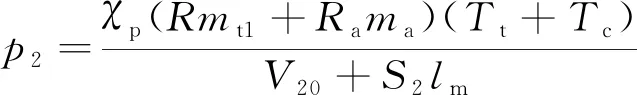
(3)

式中为压力系数；为空气的气体常数；为空气的质量；+为开氏温度；为低压室初始容积；为低压室横截面积；为位移。

火药燃烧产生的内能转化为导弹运动的动能和克服阻力做功。根据能量守恒定律可以推出低压室温度为

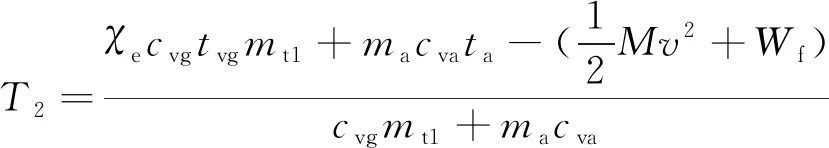
(4)

式中为能量系数；为燃气的定压比热容；为燃气温度；为空气的定压比热容；为空气温度；为导弹质量；为阻力做功。

在低压室压强大于起动压强后，燃气发生器作为活塞开始在作动筒内运动，并通过一端所连接的活塞杆，间接带动导弹运动。作动筒内活塞及活塞杆的受力情况如图2所示。

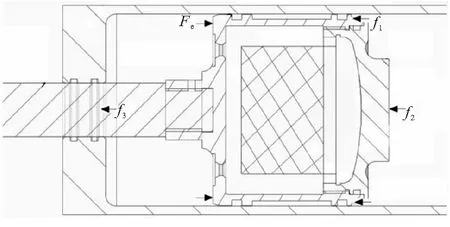
图2 活塞受力示意图

活塞在作动筒内运动，是弹射系统中最主要的作用力，燃气发生器与作动筒壁之间的摩擦力为，作动筒后段空气压缩产生的阻力为，活塞杆与作动筒间的摩擦力为。根据受力模型，可得导弹的运动方程为

=---

(5)

其中，为导弹在弹射系统中运动的推力，由低压室的压强形成。其大小为

=(1+)

(6)

摩擦力的大小需要根据所选用材料属性和配合关系得到。活塞及活塞杆与作动筒内壁之间均采用了“O”形圈密封，而“O”形圈和作动筒壁面之间的摩擦力与内部压强有关，且压强越大摩擦力越大。活塞配合处的摩擦力可以表示为

=2π

(7)

式中为密封圈处的摩擦因数；为配合处直径；为密封圈的接触宽度。

同理。作动筒后段空气阻力为，为作动筒后段初始压强，以大气压强来计算。

结合泰勒级数展开式，可以求得导弹的运动规律方程：

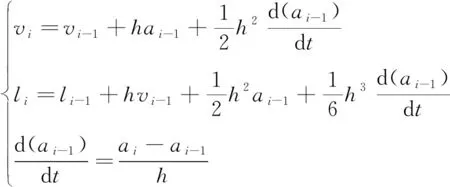
(8)

式中为当前时刻的速度；-1为前一个时间间隔的速度；为时间间隔；为当前时刻的加速度；-1为前一个时间间隔的加速度；为当前时刻的位移；-1为前一个时间间隔的位移。

3 内弹道数值模拟及试验分析

3.1 高压室装药参数

考虑到燃气发生器的结构及各项性能，必须选择合适的装药种类，并设计相应的药型和尺寸。本研究中采用了低温度敏感系数、低压强指数、高燃速的配方，选用双基推进剂作为该发生器内的装药，燃温在3000 K左右，不含金属粉，燃烧方式为内侧面燃烧，两端和外部限燃，推进剂配方性能见表2。

表2 推进剂主要性能参数

3.2 内弹道计算程序实现及优化

弹射装置的内弹道数学模型是一阶常微分方程和代数方程联立的方程组，除了已经确定的结构参数外，还有一些经验参数。其中，温度敏感系数取0.003，能量系数取0.8，流量修正系数取0.95，将药柱3～15 MPa下的燃速数据进行拟合，得到其燃速公式为=16.038 65，相关系数为0.948 6。因此，将燃速系数和压强指数分别取为16和0.21。设置时间间隔进行迭代求解，采用MATLAB编制了燃气作动筒工作过程的计算程序，并利用四阶龙格-库塔法对其中的常微分方程进行求解，从而得出高压室压强、低压室压强及导弹运动规律。

根据所编制的内弹道计算程序，按照设计好的药柱输入相应的燃面数据，对内弹道特性进行了仿真计算。同时，开展了系统联试试验，试验状态为水平发射，环境温度为5 ℃，并采用了相关传感器分别监测了高压室压强、低压室压强、运动的加速度、速度和位移。将仿真计算结果与试验结果进行对比，从而验证仿真计算结果的可靠性，结果对比图如图3所示。

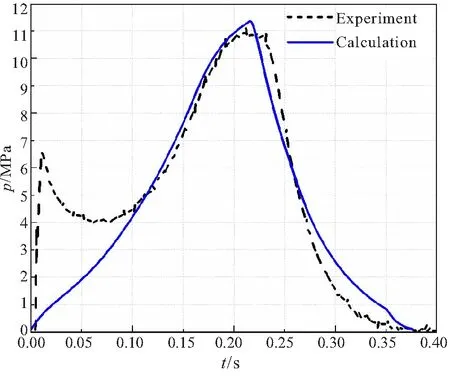
图3 高压室压强曲线

从图3可以看出，虽然100 ms后仿真计算曲线与试验曲线的趋势大致相同，但由于弹射整体过程持续时间较短，而点火压强影响约为40 ms，占据时间较长，会显著影响弹射各物理量大小，导致计算值与试验值的结果相差较大，故计算模型中需要考虑点火过程的影响。

在试验方案中，燃气发生器点火方式为点火器加引燃药盒，点火药的成分为黑火药，通过药盒固定在端盖上。在计算程序中，按照所设计的药柱及其组件输入燃面数据后，会得到内弹道相关数据。因此，可以通过增大初期的燃面数据来模拟点火压强的影响。即在弹射初期，考虑点火药条的燃面，加入到原始燃面数据中，建立了考虑点火过程的总燃面公式，即

=+[2(-2)(-2)+

2(-2)(-2)+2(-2)(-2)]

(9)

式中为总的燃面数据；为药柱的燃面；、、分别为点火药条的长宽高；为点火药条的数量。

3.3 仿真计算与试验结果对比

按照修正后的燃面数据输入后，进行了内弹道仿真计算，并与试验的曲线图进行了对比，结果如图4，其中，虚线为实验数据，实线为仿真计算结果。可以看出，高压室压强走势与试验曲线基本一致，压强峰值大小相当。点火后，高压室压强迅速升高，达到破膜压强后，燃气发生器底部的两处膜片均被冲开，高压室内压强也有所降低，但随着药柱的充分燃烧，高压室压强急剧升高，药柱燃烧殆尽后，压强也迅速降低。

低压室曲线如图5所示，随着燃气的流入，低压室压强迅速升高，在燃气膨胀的作用下，活塞在作动筒内运动，并间接带动导弹运动。低压室体积随着活塞的运动而不断增大，低压室压强逐渐减小并趋于平缓，且低压室内压强峰值不超过7 MPa。由于没有后喷，弹射过程结束后低压室内压强不再降低。导弹运动规律计算值和试验值对比如图6所示，其中加速度曲线为实测值，速度及位移为根据加速度数据所推测数据。

从导弹运动规律图中可以看出，使用四阶龙格-库塔法求解方程组得到的结果与试验结果相差不大，加速度的变化趋势基本一致，弹射结束后，导弹的最大速度为9.84 m/s。

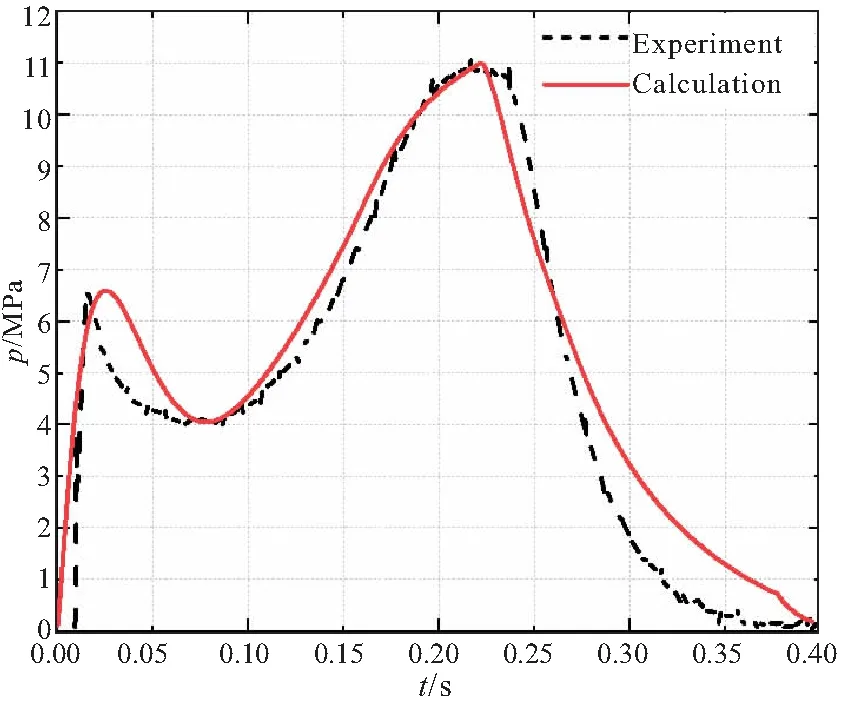
图4 高压室压强曲线(优化后)

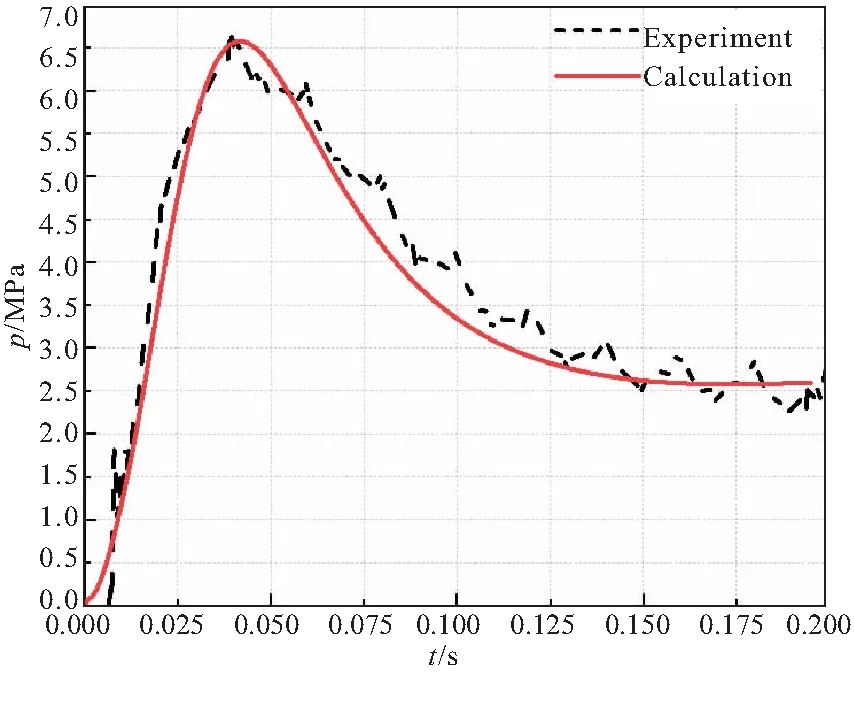
图5 低压室压强曲线

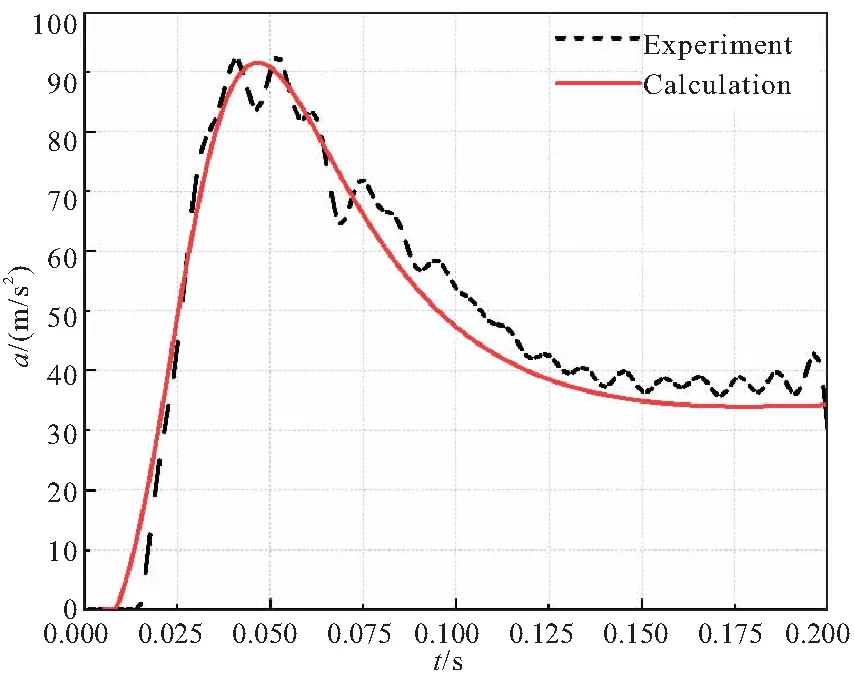
(a)Acceleration of the missile

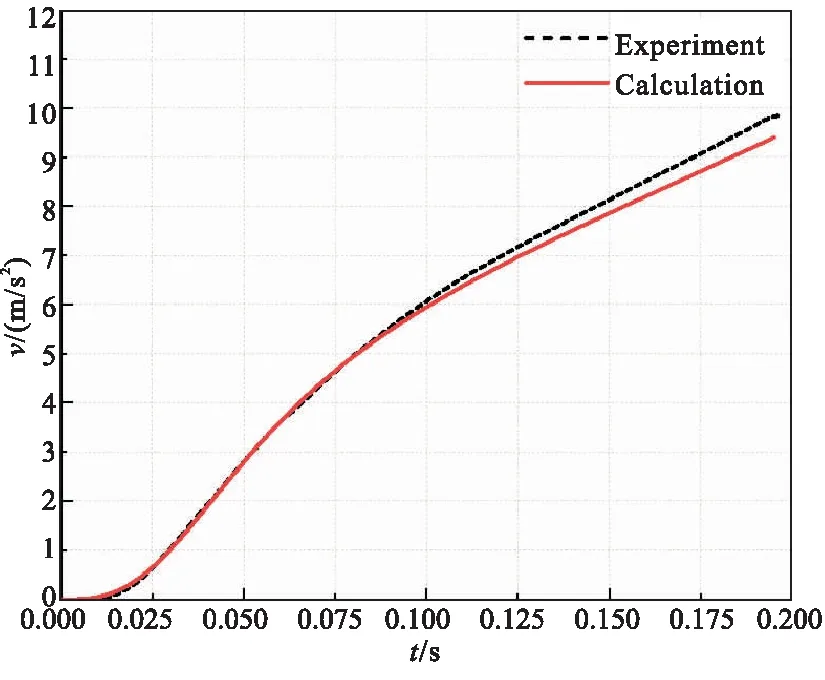
(b)Velocity of the missile

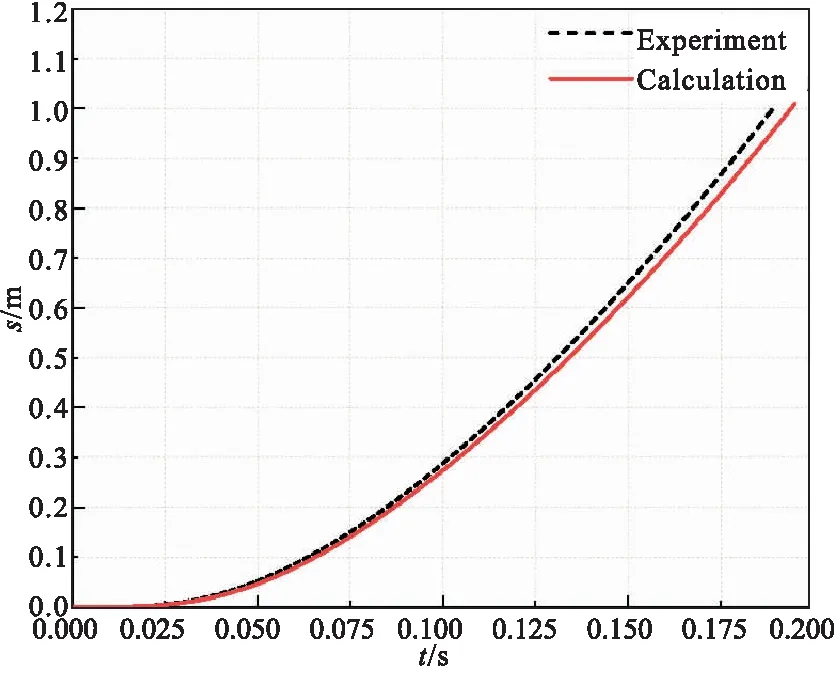
(c)Displacement of the missile

各个数据计算值与试验值的比较如表3所示，弹射过程时间(点火到燃烧室峰值压强时刻)相差为8 ms，导弹的出筒速度相差0.45 m/s，加速度相差1.16 m/s，低压室最大压强相差0.1 MPa。导弹运动的加速度先升高、后降低，速度呈线性趋势增大，计算结果与试验结果曲线吻合较好。

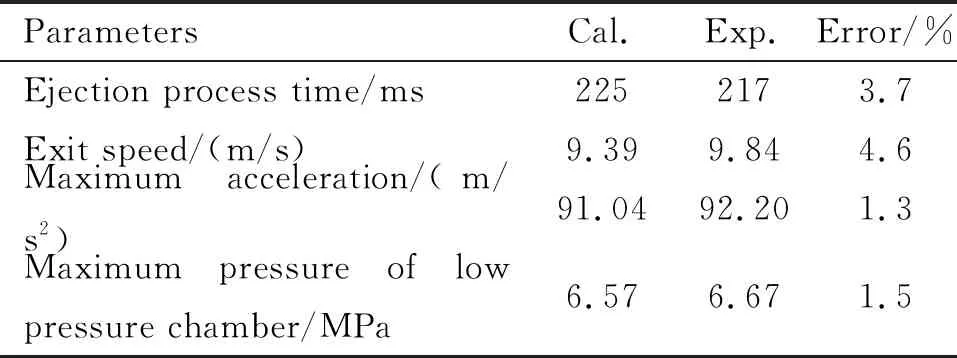
表3 计算值与试验值的比较

4 结论

本文针对某活塞式水平弹射装置的内弹道性能进行了研究，基于零维内弹道建立了弹射装置的内弹道模型，编制了仿真计算程序，并与试验结果进行了对比。

(1)所建立的零维内弹道模型与实际情况契合较好，由于弹射时间较短，点火持续时间长，且压强较大，建立了引燃药柱的燃烧模型，对内弹道仿真计算程序进行了优化，并用四阶龙格-库塔法求解内弹道方程组，优化后的程序计算结果与试验曲线的走势基本一致，弹射出筒速度和最大加速度的误差均不超过5%。

(2)弹射过程中，导弹所承受的过载较小，不超过10 g，导弹的出筒速度为9.84 m/s，未达到预期值，后续可增加燃气发生器的药量，提高燃烧室工作压强，并优化压强曲线。

本文研究的活塞式水平弹射装置的内弹道特性可为同类型的弹射内弹道性能预测提供理论指导和借鉴。