基于公路货运市场监测的铁路运价调整机制研究
张双霞,李丹丹,凌 霞
(1.中国铁路兰州局集团有限公司 货运部,甘肃 兰州 730031;2.西南交通大学 交通运输与物流学院,四川 成都 611756)
0 引言
近年来,随着电子商务和对外贸易的迅猛发展,货运需求日益增长。公路货运的运输便捷性和定价灵活性使得其货运量和货物周转量节节攀升。对于铁路运输企业而言,深入研究公路运价决定机理,全面把握现有公路货运市场环境,对于合理制定铁路运价具有重要意义。
目前已有很多学者从价格监管的角度开展公路货运价格指数的研究,包括公路货运价格指数编制[1-3]、货运价格指数影响因素分析[4-5]、货运价格指数预测[6-8]等。关于铁路市场化定价,史德耀[9]研究了铁路货运承运清算模式下市场化定价;王玉光[10]探讨了铁路货运市场化定价机制;谢如鹤等[11]研究了驮背运输的市场化定价方案。对于公铁竞争定价,国内外学者已进行了广泛研究,Pietrantonio等[12]以竞争为导向对欧洲铁路货运定价进行研究;Gorman[13]运用运筹学方法对铁路货运竞争性定价进行研究;林燕扬[14]在货运交易中引入期权理论,提出基于铁路货运长期需求的价格制定模型。这些研究对于增加铁路定价机制灵活性具有重要作用和意义。
在此,考虑在铁路、公路竞争的市场环境下,对铁路货运价格进行调控。首先,构建公路货运运价大数据平台,研究公路运价的变化情况,全面把握运输行业市场走势,探究影响公路货运价格的因素;其次,通过预测公路货运价格,优化铁路货运价格定价方案,促进铁路货运价格水平进一步贴近市场。
1 公路运输价格变化趋势及影响因素分析
1.1 公路运输价格变化趋势
从公路运价指数网获取2016—2021年间全国零担重货、零担轻货,以及9.6 m整车、13.5 m整车和17.5 m整车的单位运价数据,分析其随时间的变化趋势及影响因素。
(1)零担重货和零担轻货变化情况。公路零担货运运价变化趋势如图1所示。分析图1a、图1b中2016—2021年零担重货和零担轻货价格变化情况,其单位价格均呈现总体下降趋势。其中2016年和2017年零担重货和轻货单位价格指数较大,2016年7月和11月分别达到最高值,其余月份也基本维持在较高的价格水平上。相比2016年,2017年价格稍有下降,而到2018年后,两者的价格指数都有了明显的下降趋势,并在接下来的几年内保持数值相对稳定。
(2)不同车长的整车价格变化情况。不同车长的整车价格变化情况如图2所示。由图2可以看出,3种车型长度的整车价格具有较为相似的变化规律,价格随时间波动较为明显。总体上来看,17.5 m车型的整车价格指数较其他两者高,9.6 m车型的整车价格指数最低。3种车长的整车价格在一年中出现多个峰值,拐点较为明显,且价格变化率较大,随多个因素影响变化较为剧烈。9.6 m和17.5 m的整车价格均在2020年和2021年出现了某个单月份价格激增的态势,可能的变化因素为供需关系的影响、相关因素的波动等。
1.2 运价影响因素分析
皮尔逊系数法是英国统计学家皮尔逊提出的一种用来考察2个事物或变量之间相关强度的方法。在前期分析中可得,运价与可能的影响因素间存在着一定的相关性,因此选用皮尔逊系数法计算影响因素与运价之间的相关系数,相关系数越接近于1或-1,相关强度越强,相关系数越接近于0,相关强度越弱。
(1)零担货运价格影响因素分析。公路零担货运价格与影响因素之间的皮尔逊系数矩阵如图3所示。

图1 公路零担货运运价变化趋势Fig.1 Less-than-carload freight rate of highway
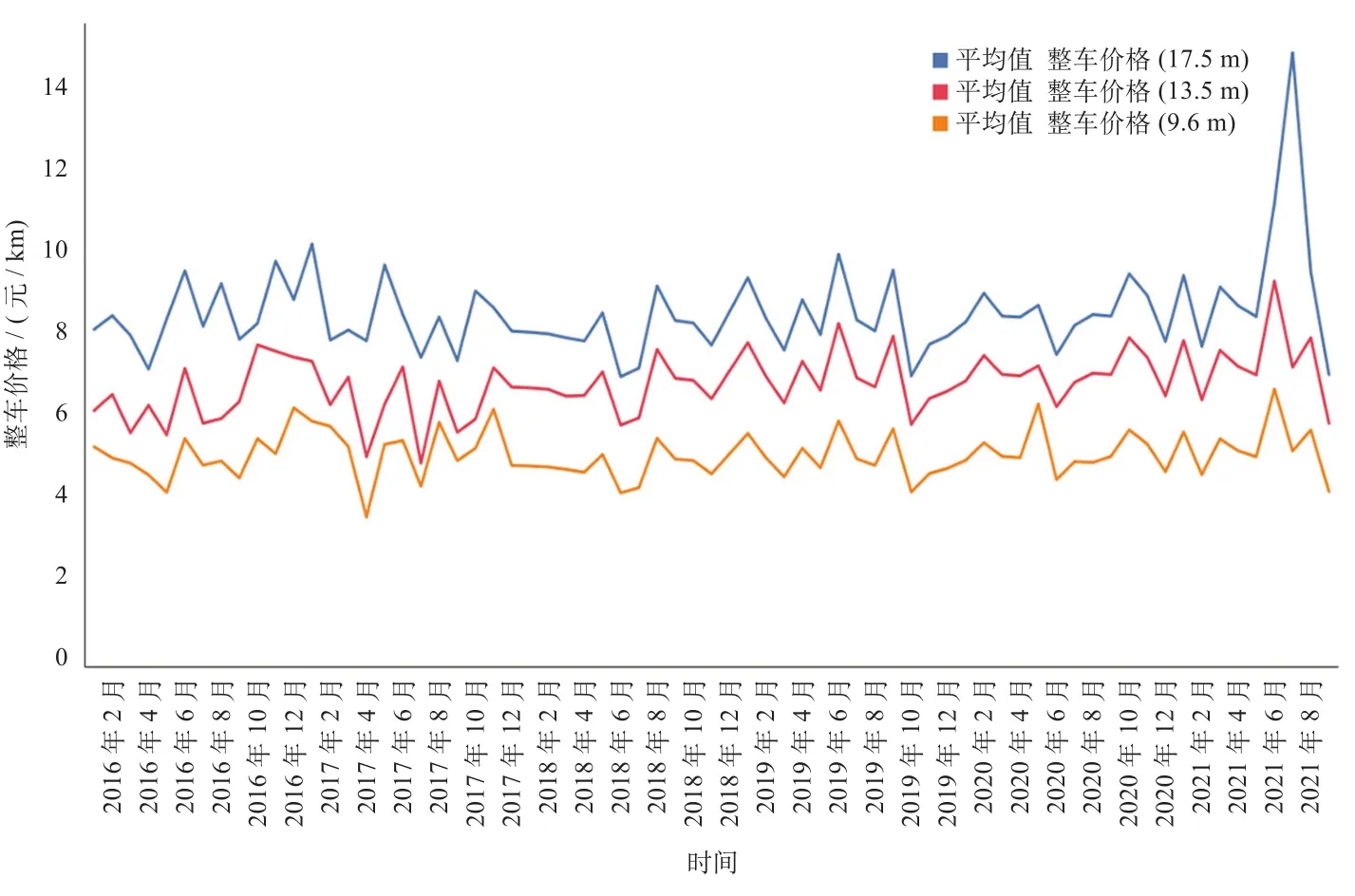
图2 不同车长的整车价格变化情况Fig.2 Freight rate of full-load truck with various lengths
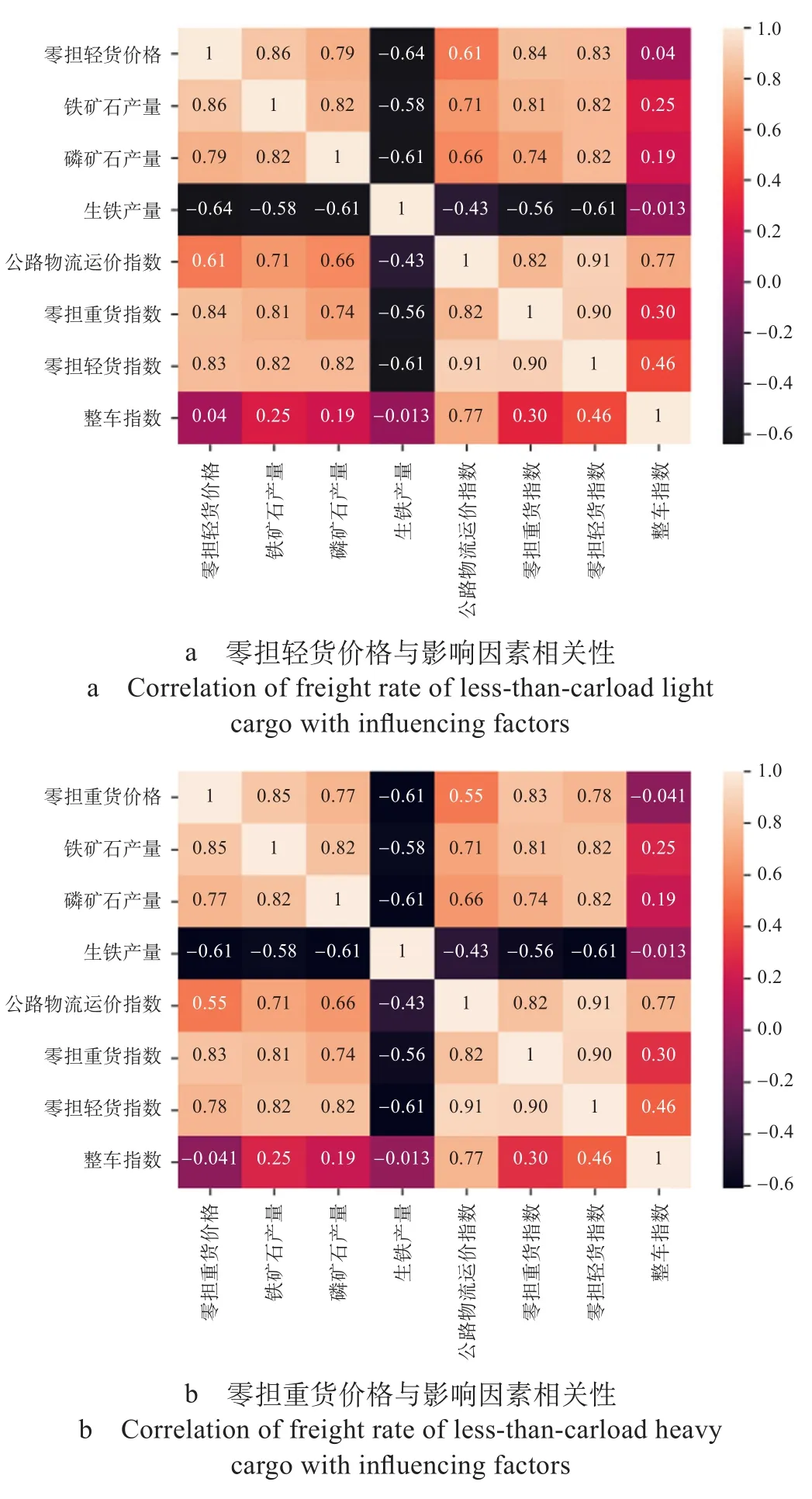
图3 公路零担货运价格与影响因素之间的皮尔逊系数矩阵Fig.3 Pearson coefficient matrix between less-than-carload freight rate of highway and influencing factors
从图3可知,铁矿石产量、零担重货指数、零担轻货指数、磷矿石产量、公路物流运价指数与零担轻货价格之间的相关系数均为正且大于0.6,这表明它们与零担轻货价格和零担重货价格之间存在极强正相关性,同时它们的变化趋势也与运价的波动趋势相似。而生铁产量与零担轻货价格和零担重货价格之间的相关系数均小于-0.6,这表明它们之间存在强负相关性,即生铁产量的变化趋势有很大可能与运价的波动趋势相反。
(2)整车运价影响因素分析。整车价格与影响因素之间的皮尔逊系数矩阵如图4所示。从图4可知,铁矿石产量、公路物流运价指数和零担重货指数的相关性系数大于0.8,表明它们与整车指数间存在非常强的相关性关系;磷矿石产量、零担轻货指数介于0.6 ~ 0.8之间,说明它们与整车指数间存在着较强的相关性关系。
(3)公路货运成本与运价相关性分析。从甘肃省高速公路运营服务中心网站提取了21万余条运输数据,结合调研所得,分车型计算了部分货车在高速公路运输过程中所产生的油耗费用、通行费用、劳动费用、折旧等。高速公路货车运输成本样表如表1所示。

图4 整车价格与影响因素之间的皮尔逊系数矩阵Fig.4 Pearson coefficient matrix between freight rate of full-load truck and influencing factors

表1 高速公路货车运输成本样表Tab.1 Highway trucking costs
2 公路运价预测
2.1 数据集准备
公路运价主要受到市场因素和运输成本因素影响。通过上述对运价影响因素的相关性分析,从以上因素中选取了独立且与公路运价的相关显著性P值在0.05以下的指标作为输入模型的特征指标,包括铁矿石原矿产量、磷矿石产量、生铁产量、粗钢产量、钢材产量、物流运价指数、零担轻货指数、零担重货指数、运输成本。对已有数据进行预处理之后,得到2020年8月至2021年8月的历史周运价数据与特征指标数据,公路运价预测模型输入数据集(示例)如表2所示。
2.2 预测模型搭建
综合考虑公路运价时间序列自身特性和多种相关特征的影响,采用加权方式将ARIMA模型和SVM模型的预测结果进行结合,以获得精度较高、误差水平低的预测结果,公式如下。

式中:Yt为预测的第t周公路货物运价,元/ (t·km);为ARIMA模型预测的第t周公路货物运价,元/ (t·km)为SVM模型预测的第t周公路货物运价,元/ (t·km);m,n为加权系数,取值范围为[0,1],m+n= 1;Yt-i为第t-i周的公路货物运价,元/ (t·km);φ(x)为第t周铁矿石原矿产量、磷矿石产量、生铁产量、物流运价指数、高速收费值所组成的向量;γ,ω为系数;a,b为常数项。
将2020年8月至2021年7月各线路各品类的历史周运价数据与特征指标数据作为输入数据,输入上述提出的ARIMA-SVM组合模型,输出得到2021年8月各线路各品类的周运价预测结果,并分析模型输出结果的精度,公式如下。

式中:δ为模型输出结果的精度;yt为运价真实值,元 / (t·km)为运价预测值,元/ (t·km)。
各线路运价平均预测精度如图5所示,总体上看,约90%的数据预测精度高于0.7,约75%的数据预测精度高于0.75,约63%的数据预测精度高于0.8,整体的预测情况较好。就具体线路而言,各货类平均预测精度低于0.7的线路有:兰州—嘉峪关、兰州—沈阳、兰州—石嘴山、兰州—太原、兰州—榆林、兰州—长沙,除兰州—嘉峪关线路外,其他主要以跨省线路为主;针对具体货类而言,轻工医药产品的平均预测精度低于0.7。

表2 公路运价预测模型输入数据集(示例)Tab.2 Input data set for prediction model of highway freight rate (example)
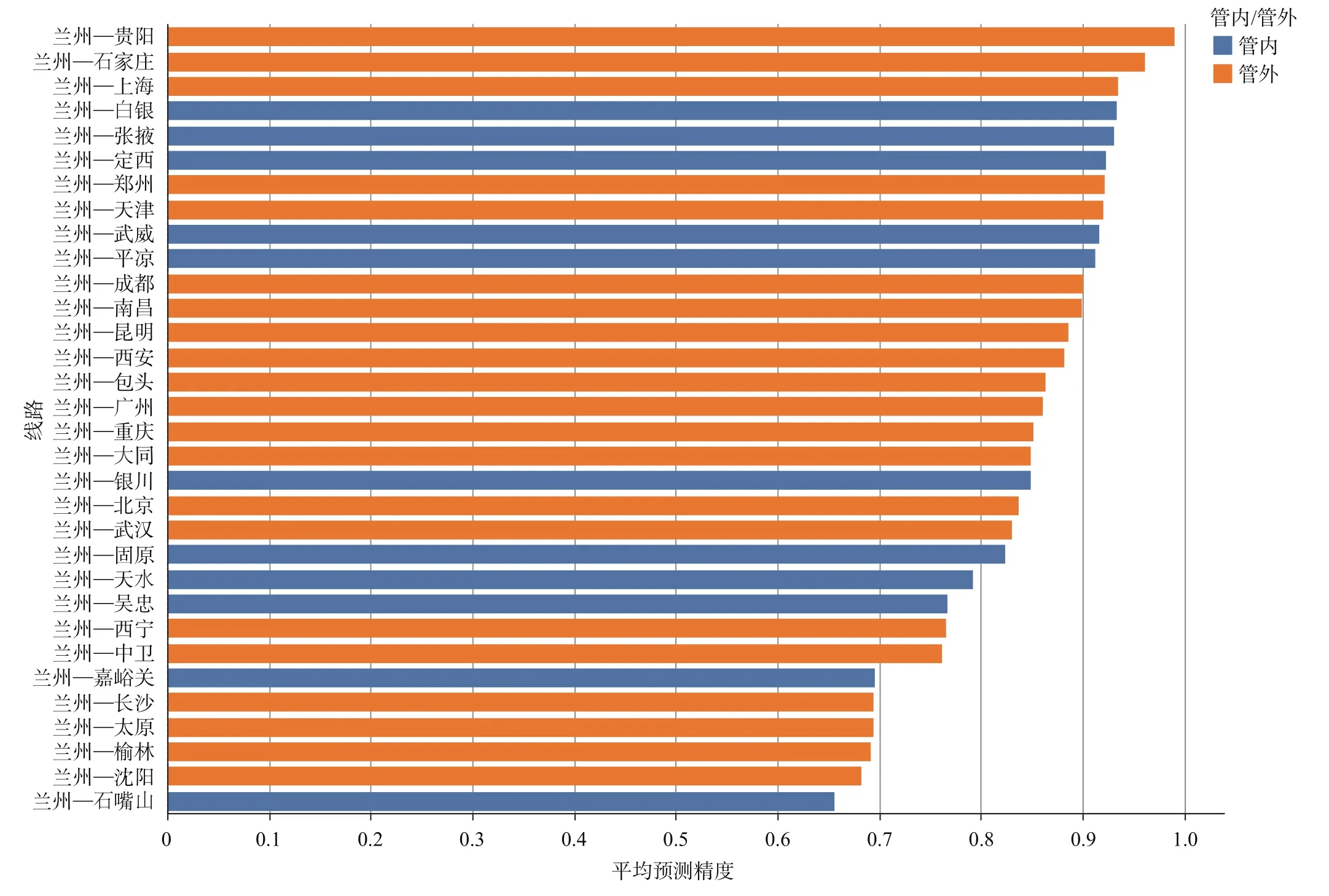
图5 各线路运价平均预测精度Fig.5 Average prediction accuracy of freight rate for each route
跨省货运涉及复杂多变的因素变量,如政策、市场环境等,从而降低了运价预测的准确性;而对于不同货类的运价预测,由于不同货类具体货物的属性特征不同,可能导致运价预测的波动。
3 基于公铁竞争的铁路货运价格制定
3.1 广义费用构建
根据安全成本及便利成本的定义,将2种成本统一称为货主满意度成本,广义费用函数计算公式如下。

式中:Ck为运输k类货物的广义费用;ok为运输k类货物的运输成本;tk为运输k类货物的时间成本;sk为运输k类货物的货主满意度成本;ω1k,ω2k,ω3k分别为运输成本权重、时间成本权重、货主满意度成本权重。
因此,选择某种运输方式的效用函数Vi可表示为

3.2 基于Logit模型的货运模式选择模型构建
货运模式选择模型构建基于以下基本假设:①假设铁路与公路互为竞争对手,货主在选择运输方式时仅考虑铁路运输或公路运输;②货主以广义运输费用作为货运方式的选择依据,当2种货运方式广义运输费用相同时,货主选择铁路运输。

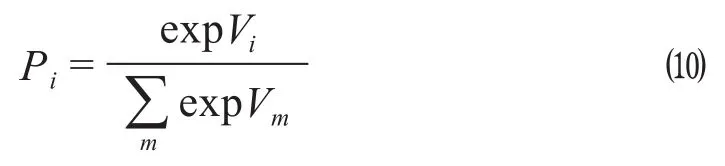
式中:Ui为第i种运输方式的感知效用;Vi为第i种运输方式的确定效用;εi为第i种运输方式未知影响因素的效用偏置项;Pi为第i种运输方式被选择的概率。
基于Logit理论,公式 ⑺ 表示货主在选择不同运输方式时,对每种运输方式不同的效用感知。其中,根据效用最大化理论,货主会选择使其感知效用最大化的运输方式,公式 ⑻ 中Pi满足公式 ⑼ 的条件。运输方式的选择枝集合由0 (公路货运)和1 (铁路货运)组成。公式 ⑽ 为假定随机项εi相互独立同分布得到的Logit模型的数学表达式。
因此,考虑货物类型的运输方式选择概率公式如下。
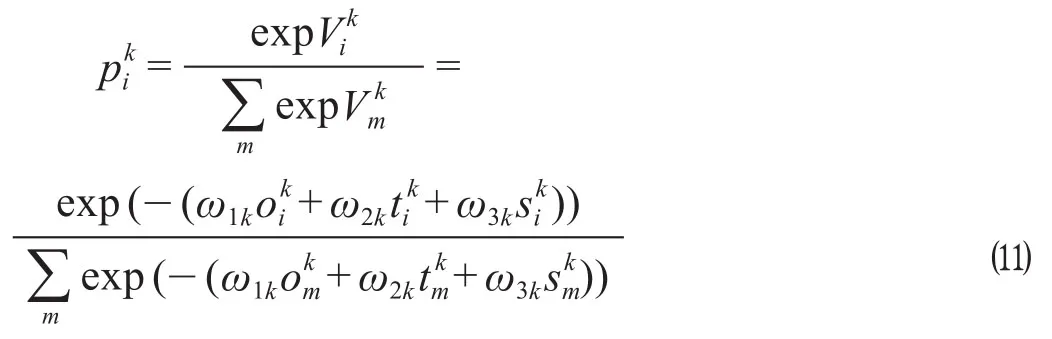
3.3 基于公铁竞争的铁路运价制定
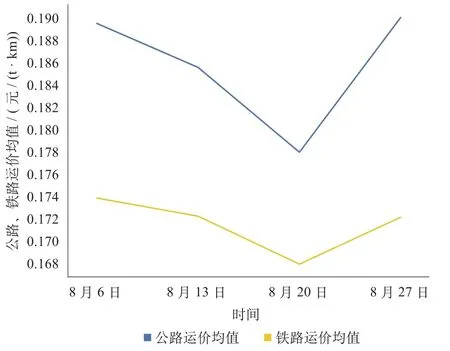
图6 2021年8月公路运价均值与铁路运价均值比较 Fig.6 Comparison of average freight rates of highway and railway in August 2021
4 研究结论
为提高铁路货运市场竞争力,研究公铁竞争环境下铁路货运定价策略。通过分析影响公路货运定价的相关因素,综合考虑公路运价时间序列特性和多种相关特征的影响,采用加权方式将ARIMA模型和SVM模型的公路运价预测结果进行结合,对公路运价进行预测。其中,ARIMA模型可以捕捉公路运价随时间变化的趋势特点,SVM模型用来捕捉铁矿石原矿产量、磷矿石产量、物流运价指数、运输成本等高关联度因素的影响,得到的公路运价预测精度较高,为下一步根据竞价确定铁路货运价格提供数据支持。在公路货运价格的基础上,建立模型对铁路价格进行调控,对于铁路运输企业完善企业价格决策体系、分担社会货物运输量、提高铁路货运市场竞争力、降低社会物流成本具有重要的现实意义。
总体而言,在竞争定价情境下,铁路运价基本低于公路运价,且铁路运价的变化趋势更为稳定。但由于不同货类、不同线路的特殊性,运价变化的趋势具有不同的特点。对于部分地区其公路定价远低于铁路成本,采取竞争定价可能存在着一定程度的偏差。因此,铁路可以采取竞争定价模型与局部调整相结合的策略,对于特殊货类和特殊线路应重视其市场运价监测,从而灵活调整铁路货运价格,提高铁路货运的竞争力。

