发电机短路工况下风电机组传动链动力响应特性研究*

白聪儿,秦美娟,孙哲杰,洪伟荣

(1.浙江运达风电股份有限公司,浙江 杭州 310012;2.浙江大学 能源工程学院,浙江 杭州 310012)

0 引 言

近年来,全国风电装机容量稳步增长。而与此同时,风电机组不断向长桨叶、大功率、柔性化方向发展,其传动链动力特性愈发复杂,这使复杂载荷条件下系统安全稳定性问题日益凸显。

为确保风力发电机组设计安全性,国内外风电行业标准、规范[1-3]对设计状态和载荷工况提出了规定,指出机组设计时应考虑发电机短路故障。因此,有必要对该工况下的传动链扭振特性开展研究。

发电机短路条件下,电磁转矩将产生一次、二次谐波分量[4],出现瞬时剧烈振荡,突变的电磁转矩将从发电机端传递给传动链轴系。风电机组传动链是柔性多阶欠阻尼系统,发电机端电磁转矩的扰动将引起各零部件转速、载荷的突变或扰动,影响各零部件安全和稳定运行。一方面,瞬时的过载将触发零部件安全限值,造成联轴器打滑等现场故障,甚至危及齿轮箱安全[5,6];另一方面,载荷波动可能引发传动链扭振,使轴系材料产生剪切应力,以及疲劳损伤[7]。根据行业统计,每年有数十起各种类型的发电机短路故障发生。

文献[8-11]基于动力学方程,研究了电磁转矩扰动下的传动链动力响应。然而,以上研究中,风电机组传动链多采用两质量块、四质量块建模,虽然考虑了传动链柔性,但机组结构仍有很大程度的简化,无法体现该工况下传动链的高频响应特性,且难以对各零部件进行载荷评估。

在此基础上,毛风麟[12]基于多自由度的传动链详细模型,开展了电磁暂态下的传动链响应研究。

随着多柔体仿真技术的发展,刚柔耦合的精细化传动链模型被广泛用于风电机组动力特性研究[13-15]。仇世龙[16]建立了传动链多柔体有限元模型,并开展了电网短路故障下的扭振特性研究,进一步分析了轴系扭振疲劳损耗。

在现有文献资料中,电磁转矩扰动条件下的传动链动力响应研究主要针对电网故障开展,面向发电机短路故障的研究较少。此外,对电磁转矩扰动条件下,传动链各级零部件载荷响应的定量分析和关键机械参数的影响研究目前尚未完全开展。

基于上述问题,笔者针对某兆瓦级双馈风电机组,建立刚柔耦合的精细化传动链多体动力学仿真模型,开展发电机两相、三相短路工况下的载荷传递特性与影响因素研究,以使该种仿真分析方法充分反映传动链动力特性,为发电机短路故障分析、传动链各级零部件安全性评估与设计提供依据。

1 刚柔耦合传动链动力学分析模型

1.1 理论方程

双馈风电机组的传动链由叶片、轮毂、主轴、齿轮箱、高速联轴器、发电机等组成。刚柔耦合动力学计算涉及到的理论方程包括系统动力学方程、齿轮箱传动方程与刚柔耦合建模理论。

其中,系统的基本动力学方程为:

(1)

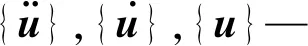
对于齿轮箱传动系统,齿轮的时变啮合刚度可表示为[17]:

(2)

式中:ωxy—啮合频率;n—啮合刚度的谐波阶次;kxy—啮合刚度均值;ksa,kca—各啮合齿轮副第α阶正弦交变分量幅值和余弦交变分量幅值。

由齿轮加工误差和安装误差引起的齿轮综合啮合误差可用正弦函数表示,即:

(3)

式中:e0,er—齿轮副综合啮合误差的均值和幅值;Tg—齿轮的啮合周期;φ—相位角。

综上所述,一对齿轮的非线性动力学方程为[18]:

(4)

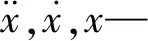
在刚柔耦合模型中,柔性体建模采用Craig-Bampton部件模态综合法[19]建模。该方法是一种子结构耦合分析方法,通过对结构进行模态分析、模态缩减、预选模态贡献叠加,构建动力学方程。

柔性体任一节点的广义坐标可表示为:

(5)

式中:x—局部坐标系在惯性坐标系中的空间位置,x=(x,y,z);ψ—局部坐标系相对于惯性坐标系原点的欧拉角,ψ=(ψ,θ,φ);q—模态振型向量。

采用模态坐标描述单元变形,可以得到任一节点的位置、速度、加速度向量[20],进而推导柔性体的总动能与总势能,质量、刚度、阻尼矩阵,将其代入拉格朗日方程,可得到柔性体运动微分方程,即:

(6)

式中:M—模态质量矩阵;K—模态刚度矩阵;D—模态阻尼矩阵;fg—广义重力;ψ—约束状态方程;λ—拉格朗日因子。

根据上述理论,即可得到传动链系统动力学方程。考虑到系统非线性、多维度、柔性化等特点,总体矩阵阶数较多,且各项系数是柔性体变形和方向的复杂函数,一般利用计算机程序完成求解。

1.2 传动链动力学模型

风电机组传动链动力学模型与拓扑图如图1所示。

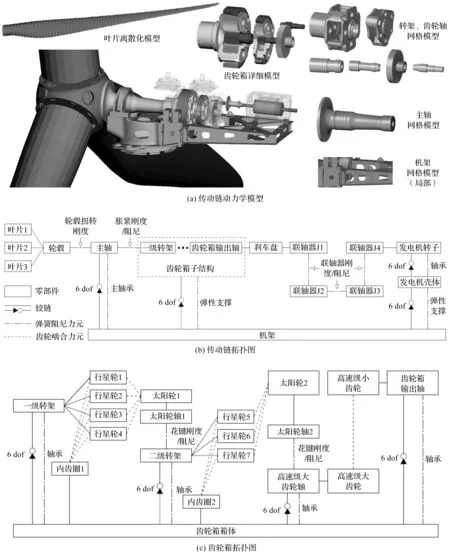
图1 刚柔耦合传动链动力学分析模型

图1中,叶片通过轮毂与主轴连接,主轴通过一级转架带动齿轮箱转动,齿轮箱输出轴直接连接刹车盘,并通过联轴器带动发电机转子转动(其中,轮毂—主轴、主轴—一级转架之间具有扭转刚度/阻尼);齿轮箱箱体与发电机壳体通过弹性支撑连接在机架上,弹性支撑力学行为采用六自由度弹簧/阻尼表示,刚度/阻尼力元具体参数由刚度试验获取或有限元计算得到;叶片采用Timoshenko梁单元建模,主轴、齿轮箱转架、各齿轮轴、机架等采用柔性体建模;轴承刚度由刚度矩阵或各向非线性刚度曲线表示;齿轮箱为两级行星、一级平行齿轮结构,齿轮啮合按照DIN 3990标准,考虑齿轮材料、摩擦阻尼、修形参数、法向侧隙等因素,计算时变啮合刚度。

为充分体现系统动力特性,笔者对联轴器采用4刚体建模,分别用J1、J2、J3、J4表示,各刚体之间由扭转刚度/阻尼连接,具体参数由制造商测试得到。

1.3 关键参数

模型中各关键参数如表1所示。

表1 模型关键参数

2 发电机短路工况动力响应特性

2.1 系统模态分析

传动链在额定工况下运行,待达到稳定状态后,笔者对其进行模态分析。

扭转方向的系统各阶固有频率与主要模态振型如表2所示。

表2 系统各阶固有频率

其中,以模态能量最大的振动作为主要振型,根据GL规范[3]92,关注的固有频率最高至齿轮箱高速级啮合频率3P,该模型为2 362.560 Hz。

模态分析结果表明:低频和高频区间传动链均存在扭转模态,基频为1.268 Hz,振动能量集中在发电机转子;风轮、主轴扭转模态对应的固有频率范围较宽,低频与高频(400.993 Hz)激励均能激发扭转振动;联轴器J2、J3扭转模态频率较高,分别为407.555 Hz和579.334 Hz;固有频率50 Hz以上的模态主要为齿轮箱零部件扭转。

2.2 两相短路工况

该节研究两相短路工况下发电机传动链的动力响应特性。

2.2.1 加载条件设置

对风轮侧加载10 m/s湍流风况下的轮毂中心载荷时序Mx,载荷由应用最广泛的风机设计软件GHbladed计算得到。

由GH bladed软件在两相短路工况下的仿真可知:由于短路工况下,电磁转矩波动频率较高、持续时间较短,故障发生期间叶片桨距角变化并不明显,使得转速、气动转矩与故障发生前差异不大。

因此,笔者仿真时风轮端输入条件按照一般湍流风况设置。对发电机转子加载两相短路工况下的电磁转矩时序,由通用电磁仿真软件Maxwell计算得到;在Maxwell中,建立电机有限元模型,对转子施加电压激励,通过电路控制,使电机发生短路,根据麦克斯韦方程组计算得到短路电磁转矩。

电磁转矩时序与频谱如图2所示。

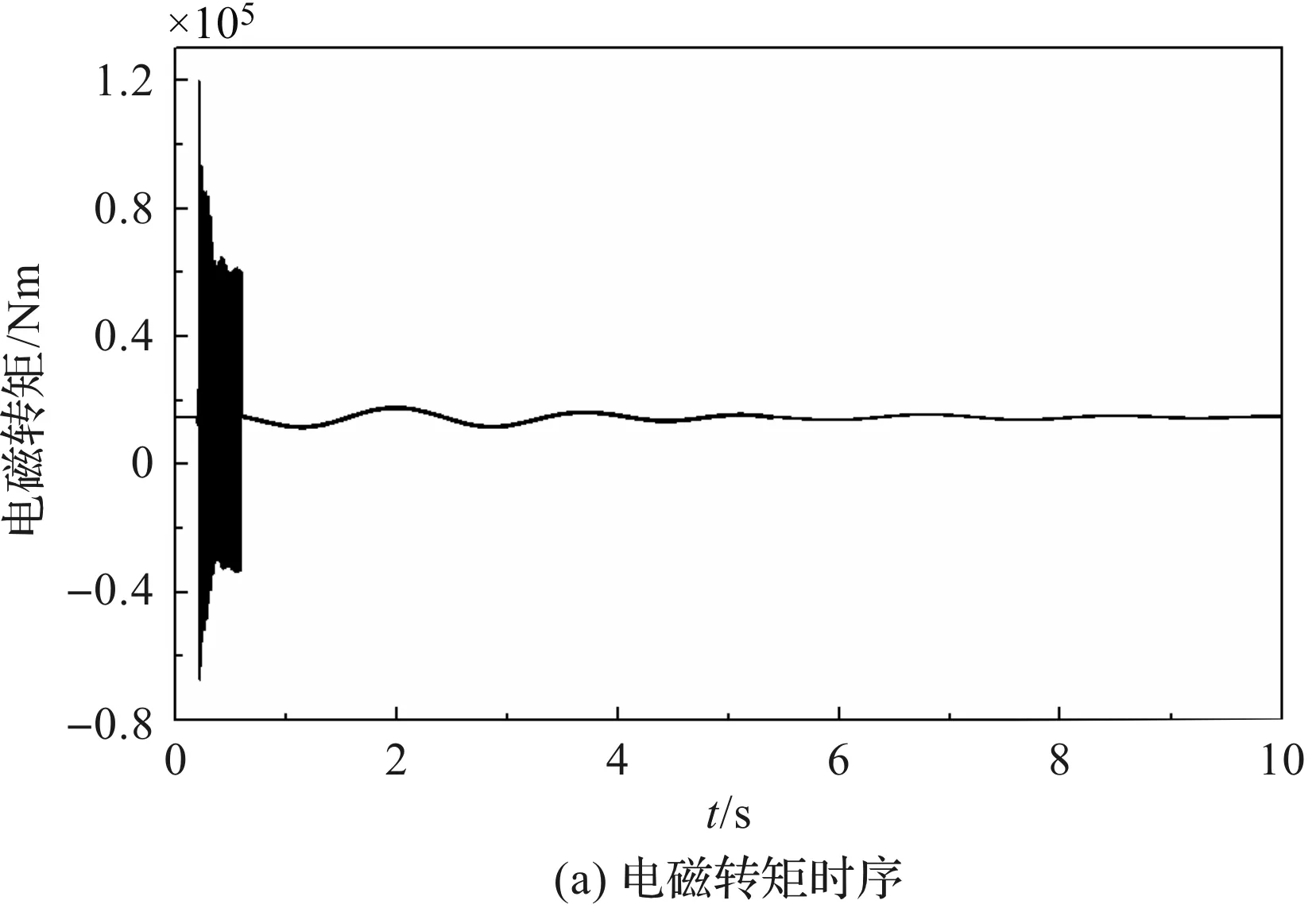
图2 两相短路工况电磁转矩暂态响应

根据图2可知:初始电磁转矩为发电机额定扭矩,0.2 s时发生两相短路。此时,电磁转矩波动瞬间增大,发生剧烈振荡,电磁转矩瞬时峰值达到120 372 Nm,为额定扭矩的8.14倍;约0.2 s后,振荡趋于平稳,幅值降低;自短路发生起,电磁转矩振荡持续0.4 s后逐渐恢复正常。

由图2(b)可知:电磁转矩主要频率分量为100 Hz;此外,还存在50 Hz分量与一些高频谐波。

2.2.2传动链动力响应

两相短路工况下,传动链各级扭矩时序如图3所示。

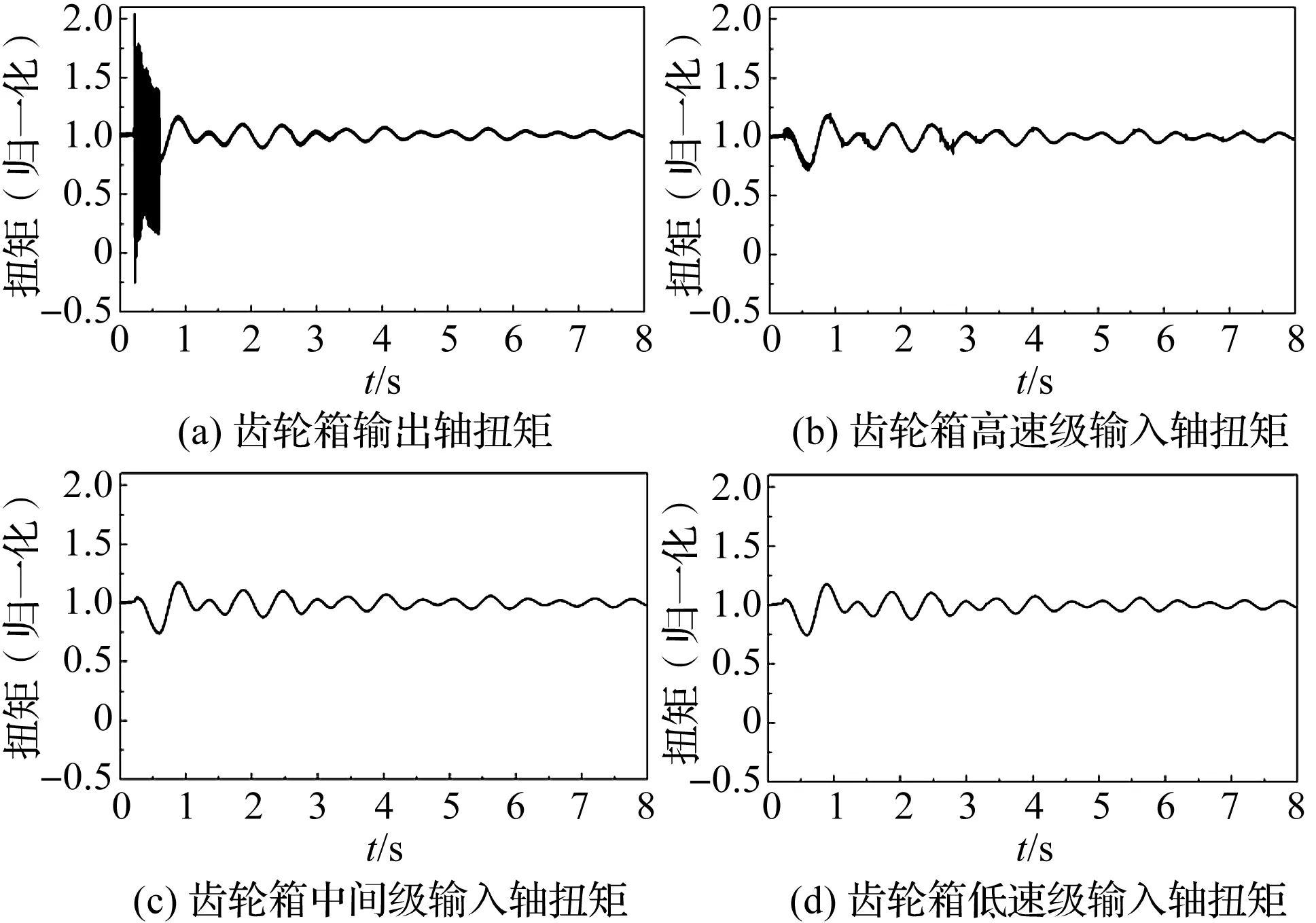
图3 两相短路工况下传动链各级扭矩响应

为了便于对比分析,笔者以0 s时刻(正常运行)的扭矩为基准,对扭矩进行归一化处理。

两相短路工况下,电磁转矩振荡过程中(0.2 s～0.6 s),传动链各级归一化扭矩峰值如表3所示。

表3 两相短路工况下传动链各级归一化扭矩峰值

两相短路工况下,电磁转矩振荡过程中(0.2 s～0.6 s),传动链各级关键频率幅值如表4所示。

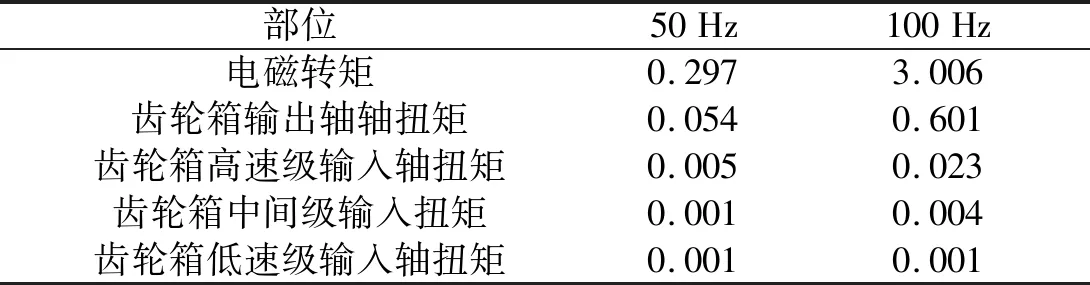
表4 两相短路工况下传动链各级关键频率幅值

根据图3、表3、表4可得:发电机端的电磁转矩振荡经过发电机转子、联轴器、齿轮箱传递后,转矩波动峰值有明显衰减。其中,齿轮箱高速级输出轴、输入轴处的扭矩峰值衰减显著,分别比上一级衰减74.7%、47.6%;而齿轮箱中间级、低速级输入端的扭矩衰减作用减弱,波动趋势较为一致。

电磁转矩50 Hz、100 Hz分量与扭矩峰值衰减规律一致,其余高频分量传递至齿轮箱输出轴时,幅值大幅降低,可以忽略不计。

电磁转矩振荡恢复后,传动系统在惯性和阻尼作用下仍持续振荡,各级归一化扭矩趋势一致,数值接近。其中,齿轮箱低速级、中间级、高速级输入轴在0.9 s存在瞬时扭矩峰值,对应的归一化扭矩为1.20,大于短路瞬间的初次传递扭矩。

2.3 三相短路工况

该节研究发电机三相短路工况下传动链的动力响应特性。

2.3.1 加载条件设置

风轮侧载荷与两相短路工况一致情况下,笔者对发电机转子加载三相短路工况下的电磁转矩时序(同样由通用电磁仿真软件Maxwell计算得到)。

电磁转矩时序与频谱如图4所示。

图4 三相短路工况电磁转矩暂态响应

由图4可知:初始电磁转矩为发电机额定扭矩,0.2 s时发生三相短路,此时电磁转矩波动瞬间增大,发生剧烈振荡,电磁转矩瞬时峰值达到98 979 Nm,为额定扭矩的6.70倍,约0.2 s后振荡趋于平稳,幅值降低,小于发电机额定扭矩;自短路发生起,电磁转矩振荡持续0.4 s后逐渐恢复正常。

由图4(b)可知:电磁转矩主要频率分量为50 Hz、350 Hz;此外,还存在明显的高频谐波。与两相短路工况相比,三相短路电磁转矩峰值和振荡幅值均较低。

2.3.2 传动链动力响应

三相短路工况下,传动链各级归一化扭矩时序如图5所示。

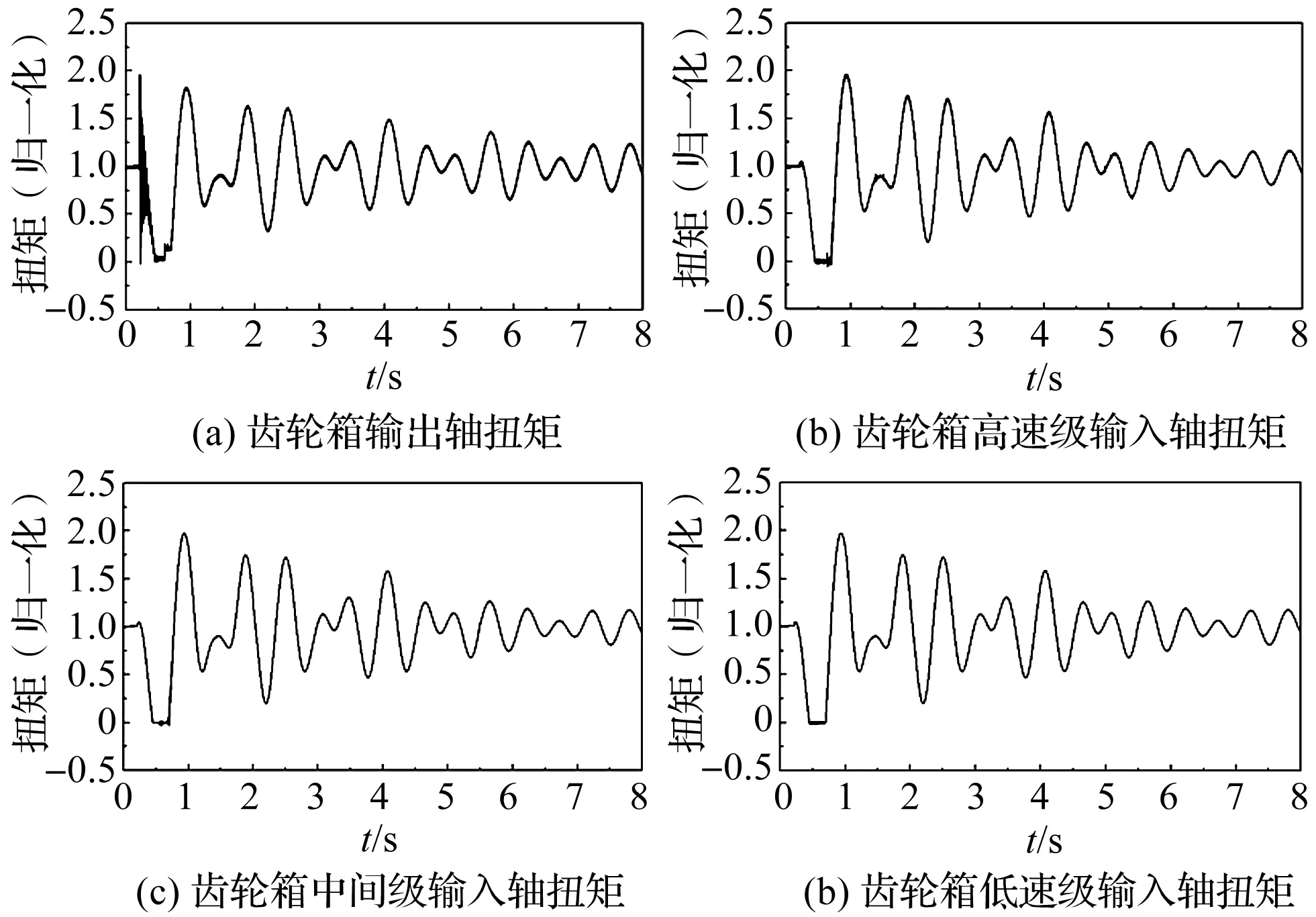
图5 三相短路工况下传动链各级扭矩响应

三相短路工况下,电磁转矩振荡过程中(0.2 s～0.6 s),传动链各级归一化扭矩峰值如表5所示。

表5 三相短路工况下传动链各级归一化扭矩峰值

三相短路工况下,电磁转矩振荡过程中(0.2 s～0.6 s),传动链各级关键频率幅值如表6所示。

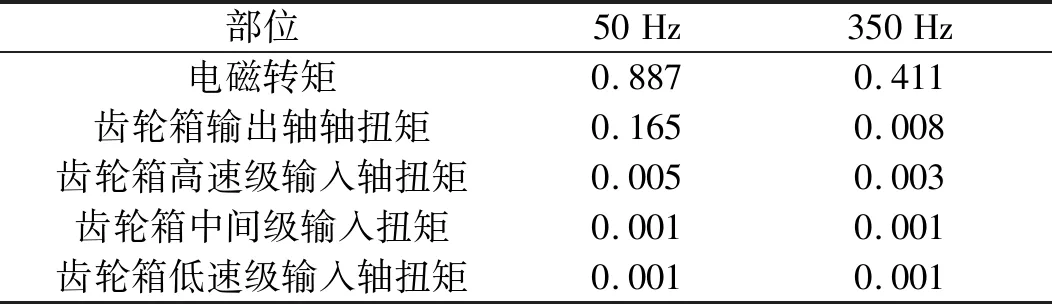
表6 三相短路工况下传动链各级关键频率幅值

根据图5、表5、表6可知:发电机端的电磁转矩振荡经过发电机转子、联轴器、齿轮箱传递后,转矩波动峰值有明显衰减。其中,齿轮箱高速级输出轴、输入轴处的扭矩峰值衰减显著,分别比上一级衰减70.7%、46.4%;而齿轮箱中间级、低速级输入端的扭矩衰减作用减弱,波动趋势较为一致。

电磁转矩50 Hz、350 Hz分量与扭矩峰值衰减规律一致,其余高频分量传递至齿轮箱输出轴时幅值大幅降低,可以忽略不计。

电磁转矩振荡恢复后,传动系统在惯性和阻尼作用下仍持续振荡,各级归一化扭矩趋势一致,齿轮箱输出轴扭矩峰值与其余各级略有差异,其余各级归一化扭矩数值接近;其中,齿轮箱低速级、中间级、高速级输入轴在0.9 s存在瞬时扭矩峰值,对应的归一化扭矩为1.96,显著大于短路瞬间的初次传递扭矩,齿轮箱输出轴在0.9 s时的扭矩接近短路瞬间的响应扭矩,与两相短路工况相比,三相短路工况恢复过程中的传动链各级扭矩波动更为剧烈。

以上基于某兆瓦级风电机组精细化传动链模型,笔者研究了两相、三相短路工况下的动力响应特性,定量分析了各级轴系载荷传递规律,可进一步为各级零部件安全性评估与传动链疲劳损伤计算提供依据。

3 关键因素影响研究

3.1 刹车盘转动惯量

该节研究刹车盘转动惯量对传动链动力响应特性的影响。风轮侧载荷与2.2节一致,发电机侧加载两相短路工况载荷,分别将刹车盘转动惯量设置为6.3 kgm2、25.2 kgm2,与第2节中的12.6 kgm2进行对比。

齿轮箱低速级输入轴与高速级输出轴扭矩时序如图6所示。

为便于展示,笔者在图6中给出了0 s～1.5 s载荷结果,1.5 s后的计算结果呈现的规律一致。

由图6可知:刹车盘转动惯量增大,低速级轴的载荷峰值略有降低,而齿轮箱高速级输出轴的扭矩发生短路后的瞬时扭矩明显增大,6.3 kgm2、12.6 kgm2、25.2 kgm2刹车盘在0.2 s左右的扭矩峰值分别为1.77、2.06和2.45;

从发电机短路工况和高速级轴的安全性考虑,刹车盘转动惯量应取较小值。

3.2 联轴器阻尼比

笔者分别将联轴器阻尼比设置为0.3、0.03,与第2节中的0.6进行对比,分析两相短路工况下传动链动力响应差异。

齿轮箱低速级输入轴与高速级输出轴扭矩时序如图7所示。

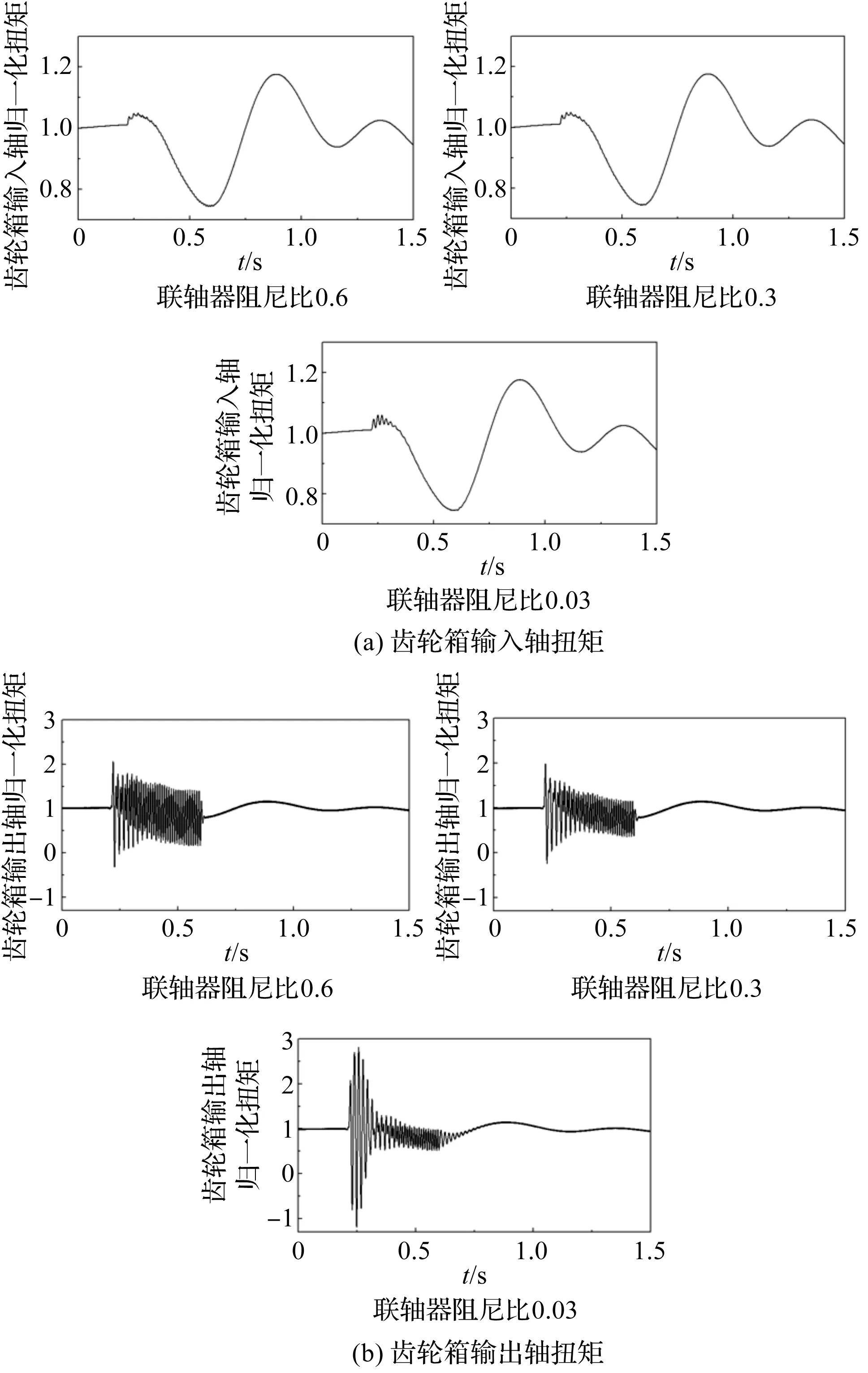
图7 不同联轴器阻尼比下的扭矩响应

由图7可得:联轴器阻尼比减小,低速级轴载荷在短路发生后的瞬时波动增大,0.4 s后扭矩波动差异不大;齿轮箱高速级输出轴的扭矩在发生短路后的瞬时随阻尼比的减小而增大,联轴器阻尼比分别为0.6、0.3、0.03时,高速轴扭矩峰值分别为2.06、2.08和2.82。

数据表明,高速轴扭矩响应与联轴器阻尼比为非线性关系,当阻尼比由0.3变为0.03时,扭矩峰值显著增大且在短时间内有发散现象。0.8 s后,3种阻尼比下的高速轴扭矩趋于一致。从发电机短路工况和高速级轴的安全性考虑,联轴器阻尼比不宜太小。

4 仿真一致性验证

为了验证上述计算结果的可靠性,笔者采用GH bladed对相同机组模型、相同工况进行仿真,开展仿真一致性验证。

由于GHbladed对传动链模型进行了两质量块简化建模,该节主要提取传动链一阶扭转频率和低速级轴的扭矩时序进行对比。

GH bladed计算得到的传动链一阶扭转频率为1.304 Hz,与表2中的一阶固有频率偏差为2.77%,在行业标准(5%)以内。

发电机两相短路、三相短路工况下的低速轴扭矩时序对比如图8所示。

图8 不同仿真方法齿轮箱输入轴扭矩时序对比

由图8可知:两种模型的计算结果趋势一致,不同软件的仿真一致性较好,证明了笔者计算结果的可靠性。

5 结束语

笔者基于Simpack/ANSYS建立了风电机组传动链刚柔耦合多体动力学仿真模型,定量分析了发电机短路工况下的传动链动力响应。

研究结果表明:

(1)笔者建立的精细化传动链动力学模型能够体现系统高频响应特性与各级零部件载荷传递规律,与第三方软件仿真一致性较好,是分析发电机短路工况下系统动力特性的有效手段;

(2)发电机短路工况下,齿轮箱高速级输出轴、输入轴处的瞬时扭矩峰值衰减最为显著,电磁转矩振荡恢复后,传动系统振荡仍然持续,齿轮箱低速级、中间级、高速级输入轴扭矩峰值相比电磁转矩有迟滞性,三相短路工况恢复过程中的扭矩波动更为剧烈;

(3)发电机短路工况下,刹车盘转动惯量和联轴器阻尼比主要影响齿轮箱高速级输出轴扭矩峰值,联轴器转动惯量偏大会导致高速轴瞬时扭矩峰值过大,联轴器阻尼比偏小同样会导致高速轴瞬时扭矩峰值过大,且出现短时间内扭矩发散,需进行合理的参数设计,以保障机组安全。

笔者的模型与相关仿真分析仅与GHbladed进行了仿真一致性验证,未开展实验或风场测试。因此,在下一步,笔者将重点开展相关的测试和验证工作。