基于NAKF和DBN的液压管路故障智能诊断方法*

姚存治,张明真,张尚然,王冠群

(1.郑州铁路职业技术学院 人工智能学院,河南 郑州 451460;2.河北石油职业技术大学,河北 承德 067000)

0 引 言

航空发动机液压管路系统是航空发动机附件装置的重要组成部分。在其服役过程中,由于疲劳、过载、碰撞等原因,容易造成其液压管路的损伤[1]。

长期以来,由振动引起的航空发动机外部管路系统失效一直是影响发动机可靠性的重要问题之一[2-4]。因此,开展航空液压管路振动失效机理研究,准确地发现其液压管路的早期故障具有重大的意义。

深度学习具有很强的自学习能力和故障分类能力。它可以直接将采集到的原始振动信号输入到模型之中,无需传统算法的特征选择和特征提取过程,因而被广泛应用于各个领域中[5-7]。作为第一个提出的深度学习训练算法,不管在应用还是算法的改进方面,研究人员都对深度信念网络进行了广泛的研究。它是目前得到研究和应用都比较广泛的一种深度学习结构[8]。

盛肖炜等人[9]提出了一种基于参数优化的变分模态分解(variational modal decomposition, VMD)和改进的深度信念网络的故障诊断方法。谭小钰等人[10]提出了一种基于深度信念网络和模糊模型的时变权重组合式预测模型,并采用该模型对光伏发电的功率进行了超短期预测。然而,上述研究主要是针对旋转机械进行故障诊断和预测,目前尚未涉及到结构复杂和噪声强大的液压管路故障的诊断方面。

航空液压管路系统由于具有高度复杂性和精密性,导致其管路振动信号呈现非线性、非平稳的特点。当航空液压管路发生故障时,其故障特征信号常常会被设备的工作频率、噪声等淹没,因此,需要对其原始信号进行降噪处理,以还原其实际的故障信号。目前常用的滤波方法有维纳滤波器(Wiener filter,WF)[11],粒子滤波器(particle filter,PF)[12],卡尔曼滤波器(Kalman filter,KF)[13]。其中,卡尔曼滤波器可随时算得新的参数滤波值,便于实时地处理观测成果,因此,卡尔曼滤波被越来越多地应用于动态数据处理中。但是传统卡尔曼滤波器只适用于处理线性信号,对于非线性信号的处理结果并不理想。因此,扩展卡尔曼滤波器(extended Kalman filter, EKF)[14]和无损卡尔曼滤波器(lossless Kalman filter, UKF)[15]应运而生。无损卡尔曼滤波器最适合于非线性信号的处理,但由于Sigma点集需满足高斯分布,从而限制了无损卡尔曼滤波器的使用范围。

因此,笔者在传统卡尔曼滤波器的基础上,利用最小二乘法修正构造的Sigma点,消除高斯分布对Sigma点影响,使其能够适应任意分布;针对管路振动信号信噪比低及非稳定性强的特点,笔者用非线性自适应卡尔曼滤波器实现信号的自适应噪声滤除,然后将滤波后的信号作为输入数据,通过深度信念网络学习深层特征;最后利用试验数据将该方法与其他故障诊断方法进行对比与分析,完成液压管路故障的智能分类识别。

1 非线性自适应卡尔曼滤波器

在航空液压管路振动数据中,除了有用信号外,还包含一些噪声。想要对液压管路的故障进行准确分类,首先需要对其振动数据进行必要的预处理,以避免有用信号被噪声干扰。

采用传统卡尔曼滤波器(KF)能够去除噪声,还原真实的故障数据,但其只适用于线性系统,且其应用对象须服从高斯分布的特点。因此,笔者在卡尔曼滤波器的基础上对其进行优化,提出了一种适应任意分布的非线性自适应卡尔曼滤波器(NAKF)。

当噪声为未知噪声,且噪声隐含在观测信号中时(叫做隐含噪声),此时隐含噪声形式如下:

(1)

对状态变量进行扩展处理,可得到增广状态矩阵:

(2)

增广状态矩阵的均值和方差分别为:

(3)

式中:m—过程噪声;l—观测噪声的维数;k—第k时刻状态下的状态矩阵。

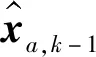
(4)

式中:N—增广状态矩阵的维数。

利用最小二乘法修正构造的Sigma点,可以消除高斯分布对Sigma点影响,使其能够适应任意分布。

最小二乘法的表达式如下:

(5)

对上式进行化简,可求得其最优解为:

(6)

综合上述公式描述,可得出非线性自适应滤波器状态预测和状态更新的表达式分别为:

状态预测：

(7)

状态更新：

(8)

根据上述非线性自适应卡尔曼滤波算法表达式可以看出,非线性自适应卡尔曼滤波器具有以下特点:

(1)非线性自适应卡尔曼滤波器在时域上具有较好适应性和递归运算效果;

(2)该滤波通过估计误差的方差和噪声协方差控制卡尔曼增益的变化,进而实现自适应的最优无偏估计;

(3)通过状态预测和状态更新交替迭代运行,使得该滤波器形成一个连续的动态系统,能够对采集的时域信号做到实时滤波。

笔者将非线性自适应卡尔曼滤波器和原始卡尔曼滤波算法(filter of Kalman,FK)、扩展卡尔曼滤波算法(extended filter of Kalman,EFK)以及无迹卡尔曼滤波算法(unscented filter of Kalman,UFK)等滤波算法应用于仿真实例的信号降噪处理中,以进一步验证它们之间的性质差异。

笔者选取原始代表信号方程为式(2),信号中加有信噪比为-12 dB的噪声,形成带有噪声的仿真信号:

S=sin(20πt)+sin(40πt)+sin(60πt)

(9)

信噪比(signal-noise ratio,SNR)是模拟结果分析常用比较的参考值,是指原始信号与无噪声的纯信号之比。信噪比越大,噪声越小。

笔者利用NAFK、UFK、EFK和KF等4种滤波方法对信号进行去噪处理,其结果如表1所示。

表1 4种滤波方法的对比结果

由表1可以看出,NAFK滤波后的信噪比为10.59,均大于其他算法的信噪比,说明NAFK算法可以获得信号的真实值,在信号处理中比传统的卡尔曼滤波效果更好。

原始信号和利用NAFK、UFK、EFK和KF等4种滤波方法处理后的时域波形图如图1所示。

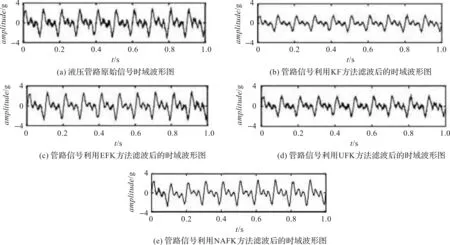
图1 原信号和滤波后信号对比图

由表1可以看出,利用NAFK方法对噪声进行处理的效果最好,这是因为该算法根据非线性自适应中的最小二乘法对sigma点进行优化,使其能够适应非线性、非平稳的液压管路振动信号。同时也可以表明,NAFK算法能够更好地识别有用信号,并且在用于估计目标的特征时能够提高振动信号的信噪比。

2 深度信念网络(DBN)

受限玻尔兹曼机(restricted Boltzmann machine,RBM)是一种神经感知器。它由一个显层和一个隐层构成,两层结构中的神经元均为二值单元,每个神经元的值为0或者1,每一层的RBM都是通过对比散度(contrastive divergence, CD)算法实现快速训练。

受限玻尔兹曼机的结构图如图2所示。

图2 受限玻尔兹曼机结构图

v—显层;h—隐层;w—显层和隐层的连接权值;a—显层的偏置向量;b—隐层的偏置向量

RBM的能量函数可以表示为:

(10)

其中,在一层RBM中,隐层神经元被激活的概率为:

(11)

式中:σ—激活函数。

2.1 DBN结构原理

DBN属于深度学习的一种常用网络结构。由于它克服了浅层网络的缺点,能更准确地发掘斜裂纹参数与其对应的振动响应之间的本质规律,提高预测的精度,近年来己经在许多领域得到了有效应用。此处,笔者采用DBN算法替代传统的浅层学习算法,并建立基于DBN的斜裂纹参数预测模型。

深度信念网络的核心是由多层受限玻尔兹曼机和一层反向传播神经网络组成,其中,受限玻尔兹曼机(RBM)的核心功能是做无监督的学习,通过递推受限玻尔兹曼机,能够将信息的特点反映到多种类的样本空间中去;然后通过调用BP反向的传导作有监督的学习,这样会使RBM把已经通过训练的特征因素设置为输入端,使用参数,经过层层调整网络,最终将模型的预测得以实现。

DBN结构原理图如图3所示。

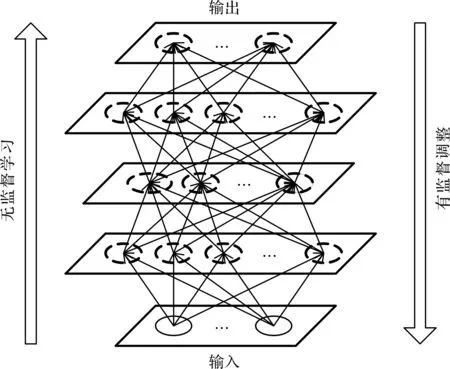
图3 DBN结构原理图

深度信念网络由输入层、隐含层和输出层组成。在深度信念网络模型构建的时候,首先需要确定隐含层层数、各隐含层节点个数、批尺寸(batch size)、学习率以及动量。深度信念网络的隐含层由若干个RBM堆叠组成,通过RBM逐层地对数据进行特征提取,得到输入数据抽象的高层特征,最后通过SoftMax将故障进行分类。

如果深度神经网络层数及隐含层节点数过少时,相比于传统的神经网络,该网络对原始数据抽象特征提取和建模能力并无优势,而隐含层和节点数目过多的话学习效率又会下降,容易引发模型的过拟合;同时,模型的训练时间会显著地增加。

目前还没有相关理论可以确定最优的网络结构,需要结合实际的问题对深度信念网络结构进行合理的构造,笔者采用正交试验,通过对模型进行反复的训练来确定网络的最佳参数,使模型的预测性能达到最佳。

2.2 模型评价尺度

采用DBN方法进行故障诊断时,和其他方法相比其主要区别在于:(1)DBN方法的故障特征提取和分类器是组合在一起的,具有一定的普适性(笔者采用DBN输入的是原始数据,不需要经过复杂的信号处理运算,不会受人为因素干扰,造成识别性能下降);(2)DBN方法是一种多层模型,相比较传统的浅层诊断方法,可有效避免发生维数灾难和诊断能力不足等问题。

因此,为了能够更好地评价分类器对不均衡样本的分类能力,在准确率的基础上,笔者同时采用混淆矩阵和观测者操作特性曲线(receiver operating characteristic,ROC)曲线进行评价。ROC反映了真阳率与假阳率的关系,曲线下的面积(area under curve,AUC)给出了分类器的综合性能,一个完美分类器的AUC为1.0,随机猜测的AUC为0.5。所以,AUC的值越大,分类器的性能越好。

3 基于DBN的液压管路故障诊断流程

基于不均衡样本驱动的民航发动机故障诊断模型主要包括DBN特征提取模型与集成分类器两部分,即先利用训练集对DBN与集成模型进行训练,然后把训练好的故障诊断模型应用到测试集进行评估。

基于NAKF与DBN的液压管路故障诊断流程,如图4所示。

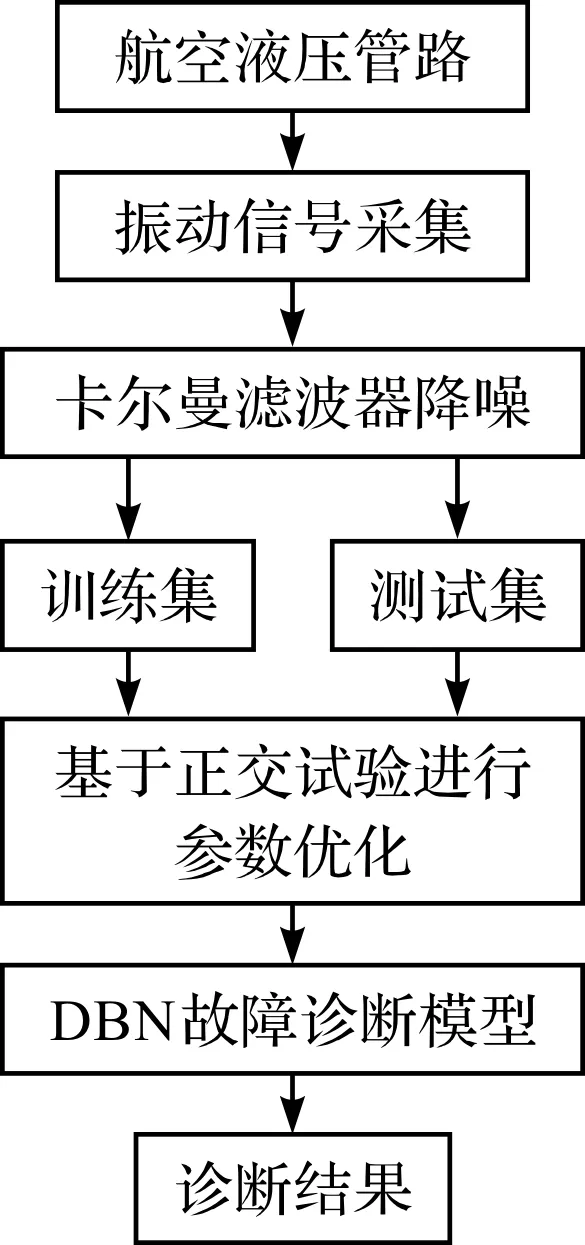
图4 基于NAKF与DBN的液压管路故障诊断流程

基于DBN的航发液压管路故障诊断方法详细步骤如下:

(1)收集故障样本数据,构建故障样本集;

(2)利用卡尔曼滤波器对振动信号进行降噪处理;

(3)对降噪后的样本进行训练集与测试集的划分;

(4)采用正交试验对DBN的参数进行选取;

(5)利用训练好的DBN特征提取模型对测试集进行故障诊断;

(6)统计模型故障诊断结果,选取相应指标进行评估。

4 实验及结果分析

4.1 实验说明

笔者选取管径为14 mm、壁厚为2 mm、长度为50 mm、材质为304不锈钢的航空液压管路作为实验对象,其中,直管6种(无故障管1种、故障管5种)、90°弯管3种(无故障管1种、故障管2种),每种管路上选取3个测点(直管测点分别在管路的1/4、中点与3/4处,弯管测点分别在两个弯点以及中点处)分别命名为K1、K2、K3。

液压管路具体参数如表2所示。

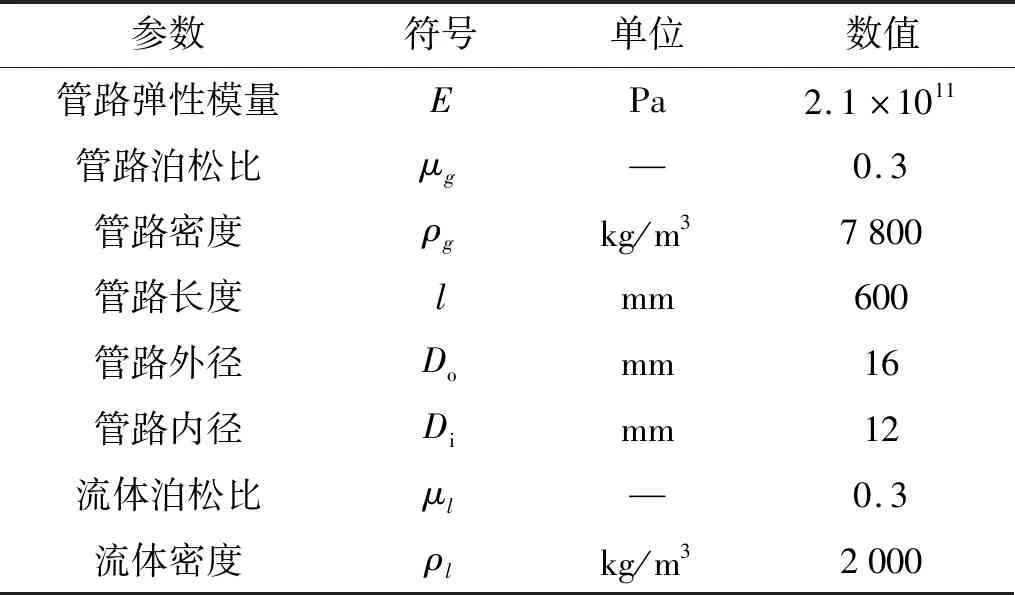
表2 液压管路的材料参数和几何尺寸

为了对上述液压管路进行有效的故障诊断实验,以得到更具有代表性的故障特征数据,笔者首先对该管路进行故障植入。笔者所选取的基本管路故障类型为:轴向裂纹、径向裂纹以及凹坑。所有的裂纹故障均由激光线切割植入,裂纹长度均为10 mm,深度为1 mm。凹坑故障则由模拟管路碰撞得来,用重器对管路进行敲击从而植入凹坑故障。

具体的液压管路故障情况如表3所示。

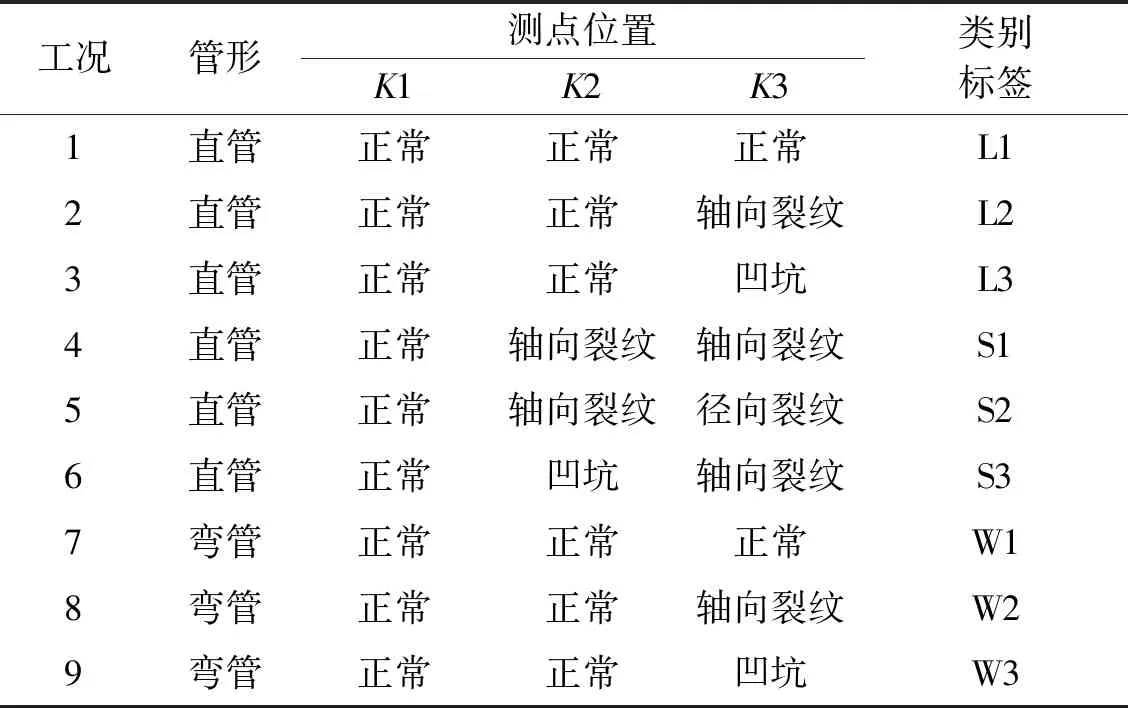
表3 管路故障情况

为了验证上述故障诊断方法的有效性,笔者针对航空发动机液压管路进行故障植入实验,采集相关数据,并对其进行处理。

此处的液压管路试验装置主要由电动机、柱塞泵、变频器、节流阀、油箱、管路系统和控制系统等组成。实验中,笔者使用3个加速度传感器同步采集液压管路的振动数据,分别在测量管路两端和管路中间3个位置的加速度。

液压管路振动数据采集实测图如图5所示。

图5 液压管路振动数据采集实测图

试验参数设置如表4所示。

表4 液压直管材料参数与几何尺寸

4.2 数据集创建与DBN参数设计

由于液压管路的故障特征信息受管路复杂结构和流固耦合振动特性等因素影响,导致其早期的故障表征不明显,为避免故障信息遗漏,笔者将滤波后的振动信号以相等的窗口长度进行划分(每个样本包含600个数据点,每种故障400个样本,即生成一个3 600×600维的数据样本),并将数据集划分为训练集与测试集(训练样本数量和预测样本数量的比例为8∶2)。

已有的研究发现,对DBN分类能力影响较大的参数主要由:隐藏层数(l)、隐藏层单元数(e)、批尺寸(batch size)、学习率(alpha)和动量(momentum)。利用正交试验方法设计DBN参数能够找出诊断结果的主要影响因素,并且效率较高,各个参数的取值参考李海平等人在相关文献中的设定,正交试验的因素与水平为:

A:隐藏层数(l):l1=2,l2=3,l3=4,l4=5;

B:隐藏层单元数(e):e1=512-512……,e2=512-256……;

C:批尺寸(b):b1=15-5,b2=20-20;

D:学习率(a):a1=0.000 1,a2=0.001;

E:动量(m):m1=0.9,m2=0.8;

因此,笔者定义的正交试验设计属于混合水平,所用正交表为L8(41×24),其中,平均值m值和极差R的计算公式如下:

(12)

R=max{m1,…,mqi}-min{m1,…,mqi}

(13)

式中:qi—因素的水平数;y(K(qi))—第Ki个因素第qi个水平的结果;R—极差,可以为各因子对最后结果的影响程度排序。

正交实验参数表如表5所示。

表5 正交实验参数表

由表5可以看出:2号试验(A1B2C2D2E2)实验准确率最高为99.72%,进一步通过平均值K和极差R分析当前结果是否为最优方案;通过R值可以发现,A因素(隐藏层数,即RBM个数)对准确率的影响最大,其他因素对准确率影响不大;由K值分析之后可得,A1B1C2D1E2(隐藏层数为2,隐藏层单元数为512-512,批尺寸为20-20,学习率为0.001,动量为0.9)组合可能准确率更高,实验得到结果为99.72%,进一步说明当对准确率影响大的A因素确定后,其他因素对结果影响较小。

为验证DBN模型的稳定性,笔者将数据集采用随机抽取的训练方式(DBN的结构参数为A1B2C2D2E2)进行实验,得到了管路数据测试集的预测值与真实值的对比结果,如图6所示。

图6 管路数据测试集训练图

由图6可看出,测试集中只有一个样本分类错误,证明其诊断准确率较高。

为了验证其算法,笔者选取3种方法进行对比(统一基于同一数据集,并降维到300)。各自算法相关参数设置如下:

(1)NAKF+BPNN。采用300-128-9,学习率a=0.000 1;

(2)NAKF+SVM。核函数选择径向基函数(radial basis function, RBF),设置惩罚因子c=0.062 5,核函数参数g=0.062 5,停止训练误差精度设为0.000 1;

(3)原始信号+DBN。DBN的参数选择隐藏层数为2,隐藏层单元数为512-256,批尺寸为20-20,学习率为0.000 1,动量为0.9。

为了避免偶然性,笔者对其进行了10次随机试验,并将10次试验的分类正确率进行平均处理。

最终得到了数据集的训练结果,如图7所示。

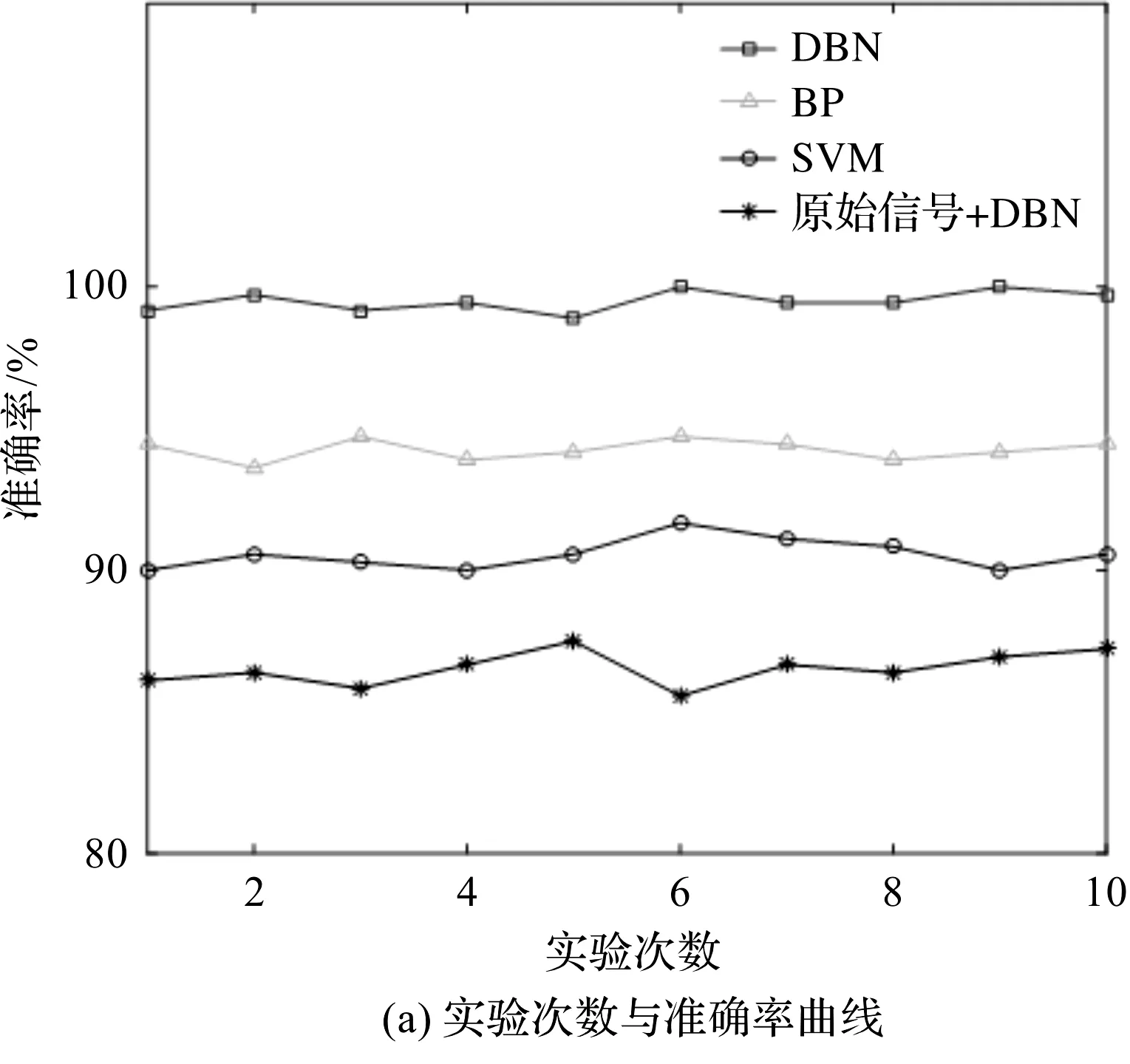
图7 管路数据诊断的平均准确率

由图7可见,NAKF-DBN算法在训练测试集上准确率达到99.50%。传统的浅层算法如BPNN和支持向量机的分类准确率最高不超过95%,而未经NAKF滤波的DBN网络准确率只有86.58%,并且为了更加直观地展示各个模型的实验效果,各个模型的混淆矩阵以及各个模型的ROC如图8～11所示。

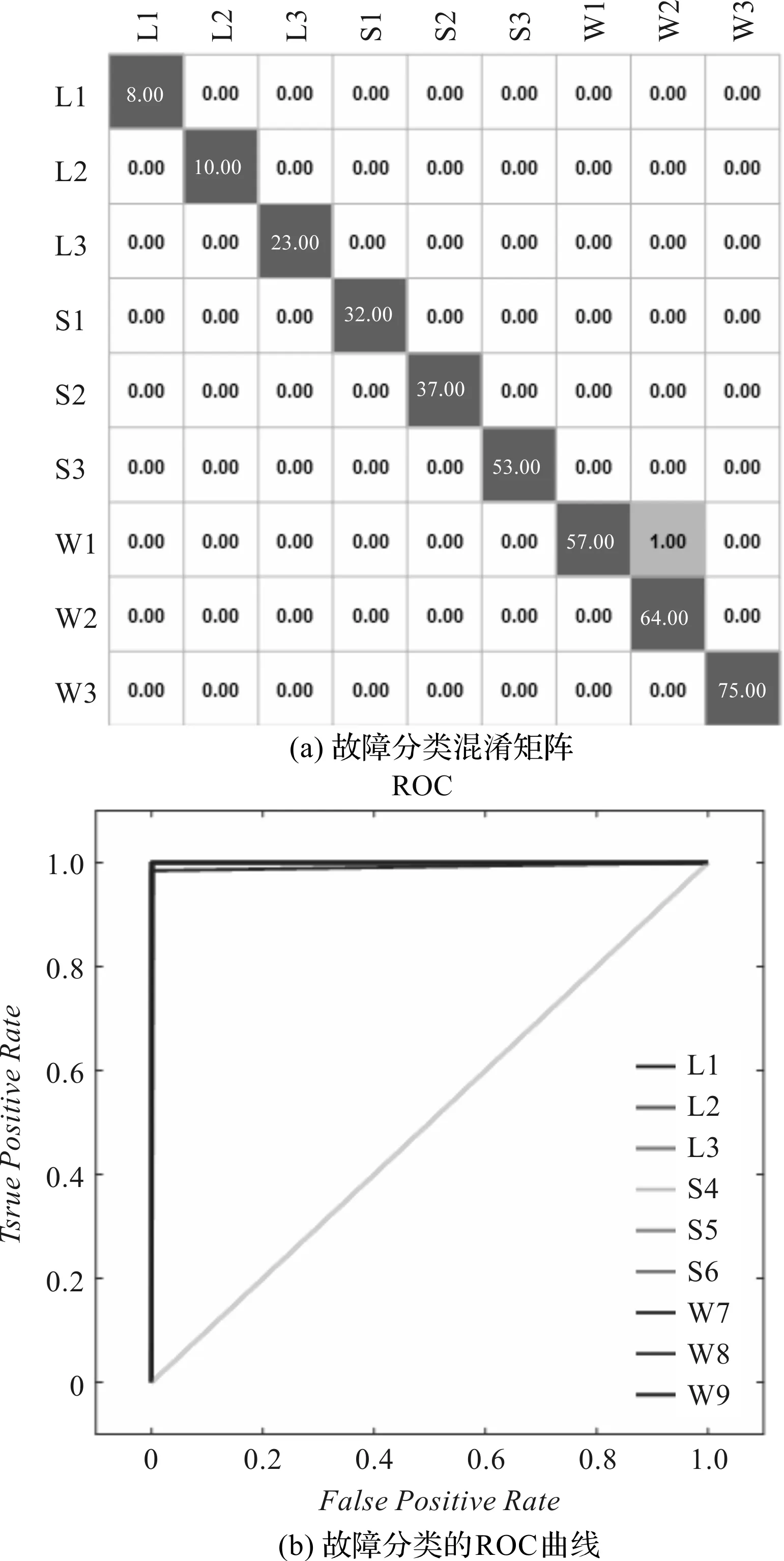
图8 NAKF-DBN模型识别结果

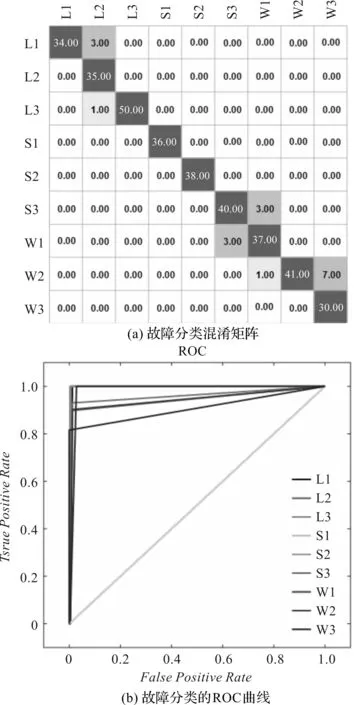
图9 BPNN模型识别结果

图10 SVM模型识别结果

图11 原始信号+DBN模型识别结果

在该次分类中,各种模型的混淆矩阵如图(8～11)中的(a)图所示,其中,NAKF-DBN的正确识别率最高,为99.72%,只有一个弯管正常状态被错误的识别为裂纹故障状态;未经过滤波处理时的准确率最低,为91.67%,说明未滤波处理直接进行故障分类会导致错误率提高;同时,通过观察错误率发生的情况,可以发现被错分的样本基本集中在矩阵右下角,说明弯管正常与故障状态比较容易混淆。

NAKF-DBN与DBN模型的ROC曲线如图(8,11)的(b)图所示,可以发现,DBN利用经过NAKF去噪后的信号作为输入比单一的DBN利用原始数据作为输入分类能力强。

BPNN与SVM模型的ROC曲线如图(9,10)的(b)图所示,可以看出,NAKF-DBN的分类能力要好于BPNN与SVM,说明笔者模型的分类能力要好于传统浅层网络。

通过上述对比实验,说明在结合DBN与滤波技术之后,笔者提出的模型对于高维度、多种类故障样本有很好的分类能力。

5 结束语

航空发动机中的液压管路早期故障信号微弱,且其受噪声污染严重,致使液压管路故障识别困难,针对这一问题,笔者提出了一种基于非线性自适应卡尔曼滤波器(NAKF)及深度信念网络(DBN)的液压管路故障状态识别新方法,即首先在传统卡尔曼滤波器的基础上,利用最小二乘法修正构造的Sigma点,消除高斯分布对Sigma点影响,并针对管路振动信号信噪比低及非稳定性强的特点,用非线性自适应卡尔曼滤波器实现信号的自适应噪声滤除;然后将滤波后的信号作为输入数据,通过深度信念网络学习深层特征;最后利用试验数据将该方法与其他故障诊断方法进行对比与分析,完成对液压管路故障的智能分类识别。

研究结论如下:

(1)在传统卡尔曼算法的基础上,使用非线性自适应滤波器进行了优化,消除了高斯分布对Sigma点的影响,提高了真实信号的还原度,有效解决了卡尔曼算法的适应性问题。并通过仿真实验分析确定了该滤波方法的可行性,对比标准KF,EKF,UKF方法对仿真数据的降噪效果,证明降噪后的信号具有更高的信噪比;

(2)为解决工程实际中液压管路结构复杂、故障类型多样造成的诊断困难问题,笔者利用非线性自适应卡尔曼滤波器去除噪声,然后利用DBN学习深层故障特征,进而实现了航空液压管路的智能诊断。将原始振动信号和滤波后的信号作为DBN输入,后者的分类准确率在99%以上,验证了NAKF对实际液压管路振动信号去噪的有效性;与SVM,BPNN等传统浅层网络模型进行了对比,结果表明:在分类准确率和ROC曲线两类评价指标下,笔者提出的分类模型准确率最高,对每种故障都有良好的分类能力。

综上所述,针对航空发动机外部液压管路的结构特点,探讨更为简洁、高效和通用的空间液压管路故障诊断模型,这是笔者下一步需要深入研究的重点。