基于机器学习方法的桥梁损伤状态识别

李超齐

(中铁十八局集团有限公司，天津 300000)

0 引言

最近两年，以大数据、人工智能为基础已成为当下各行各业发展的重要趋势，人工智能正在加速形成自己的产业链。我国作为桥梁大国已有几千年的发展历史，拥有规模庞大的桥梁资产[1]。我国桥梁由古至今分为三种基本桥型：连续梁、简支梁、连续刚构。但随着技术的进步以及各地区对桥梁需求的不同，又演化出基于三种桥型的几百种不同类型的桥梁。在此背景下，由于不同类型的桥梁施工工艺不同、建造方法不同，导致维修、养护方法也有所不同。如何能从这些桥梁数据中快速、准确地将不同类型的桥梁进行分类并且充分识别桥梁的振动、变形、应力、裂缝等指标，并进行高水平的运营、管理、维修、养护具有十分重要的意义[2，3]。对比国内外研究发现，国外建筑行业利用人工智能识别图片的文献很少，国内建筑行业几乎没有。为此，本文利用大数据与人工智能技术以三种基本桥型的图片数据作为分类与预测对象，通过建立健康桥梁图像训练模型，识别桥梁的结构状态，为桥梁状态在线评估提供新的思路。

1 桥梁图像预测方法

桥梁状态对于后期运营、管理、维修、养护十分重要，本文选择的监测指标包括连续梁、简支梁、连续刚构承受车辆载荷、风载荷后的桥梁变形、位移和振动幅值。Weka图像数据挖掘平台是在Java环境下开发的机器学习以及数据挖掘软件，平台内嵌套了多个数据挖掘方法，可以实现对图片数据的预处理、分类、关联规则、交互式界面可视化等。基于Weka图像数据挖掘平台，采用朴素贝叶斯、神经元网络、简单逻辑回归3种方法分别建立桥梁图像识别模型，选择其中结构状态较好的桥梁按照简支梁、连续梁、连续刚构3种类型进行细分，再按建筑材料分为钢筋混凝土桥梁、预应力混凝土桥梁。采用机器学习方法对图像中桥梁变形、振动幅值等参数进行训练，形成对不同类型桥梁挠度、变形、振动的判别标准。

1.1 朴素贝叶斯分类器

朴素贝叶斯定理可以表示为[4]：

(1)

其中：X为隐藏节点个数；y为所观察到的数据。

在实际检测时，往往采用多种参数及条件(称为成分xi)来推定事件是否发生。

1.2 神经元网络分类器

多层神经网络也可以用最小二乘法来表示，神经网络的误差矩阵为[5]：

(2)

其中：N为节点数；yi为节点i的理想输出；oi为节点i的实际输出；ω为权重矩阵。

1.3 简单逻辑回归分类器

简单逻辑回归分类函数为：

h(x)=hθ(x)=θ0+θ1x1+θ2x2+，….

(3)

其中：θi为回归系数。

分类函数对应的错误估计函数为：

(4)

其中：m为样本个数；hθ(x(i))为预测值；y(i)为真实值。

2 数据评价与预测

2.1 数据处理与评价

本次实验共有12 000张桥梁图片数据，将其中的3 500张连续刚构、3 500张连续梁、3 500张简支梁共10 500张健康状况的桥梁图片数据作为训练集，剩下的1 500张图片(3种类别桥梁各500张)数据作为测试集，其中有150张图片(3种类别桥梁各50张)数据存在不同类型的病害。借助Weka 开源平台下的imagefilter图片过滤器对图片训练集和测试集进行特征值提取，如果Weka 可以找到所有的图像文件并且没有其他错误，那么将会看到添加到数据集的新属性均为数字属性。具体预测步骤如图1所示。

图1 预测步骤

2.2 算法对比

样本数据分类是否成功，主要从准确度、详细精度和节点错误率3个方面比较分析。本文以10 500张健康状况的桥梁图片数据作为训练样本，1 350张健康状况的桥梁图片和150张含有病害的桥梁图片作为测试样本。每张图片为一个单元节点，分别采用朴素贝叶斯分类器、神经元网络分类器、简单逻辑回归分类器对10 500张健康状况的桥梁图片进行训练，然后基于训练结果再对1 350张健康状况的桥梁图片和150张含有病害的桥梁图片进行识别，需要同时识别出桥梁类型和健康状况。3种算法样本识别准确度如表1所示。

由表1可以看出：3种算法的识别效果都不错，朴素贝叶斯>神经元网络>简单逻辑回归>63%。3种算法准确率的残差图如图2～图4所示。

表1 3种算法样本识别准确度

从图2～图4可以看出：朴素贝叶斯分类器分类正确的准确率平均值较高，接近75%，其散点比较集中，没有太大的波动，比较稳定；神经元网络分类器分类准确率接近70%，其稳定性略逊于朴素贝叶斯网络分类器；简单逻辑回归分类器分类的准确率只有63%，散点分布在各个位置，不集中，其效果差于前两种分类器。

样本数据经过Weka平台十折交叉验证后，3种分类器的详细精度分析分别如表2～表4所示。以连续刚构为例，正例比率=连续刚构图片预测数量/连续刚构图片真实数量，负例比率=其他类型桥梁识别为连续刚构数量/其他类型桥梁数量。精准度=(识别正确的正例+识别正确的负例)/桥梁图片样本数量，查全率=预测正确的正例/(预测正确的正例+预测错误的负例)，调和平均数是各统计变量倒数的算术平均数的倒数，ROC面积为评价模型优劣的指标，反映各分类器对样本的排序能力。

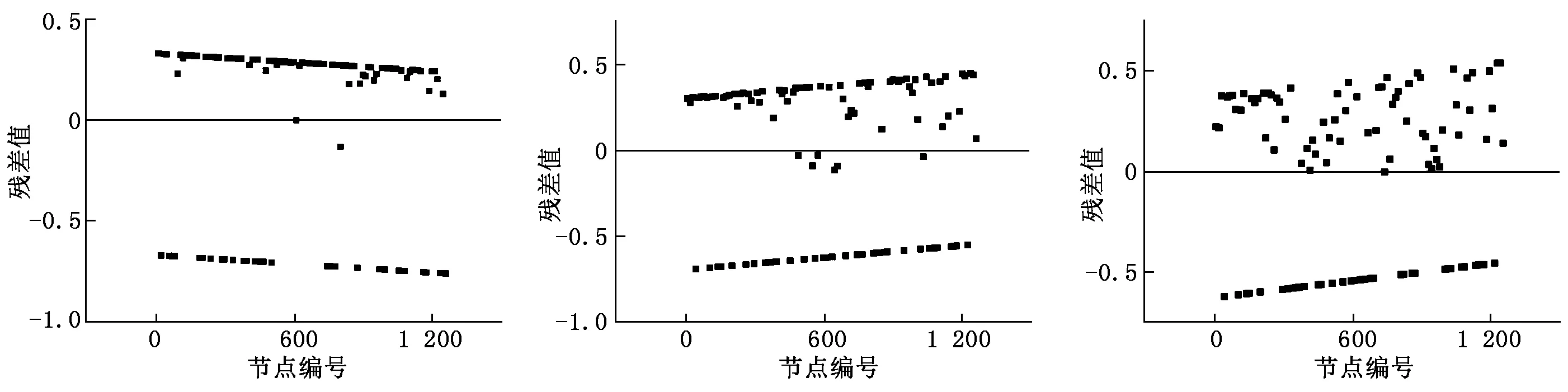
图2 朴素贝叶斯算法残差图 图3 神经元网络算法残差图 图4 简单逻辑回归算法残差图

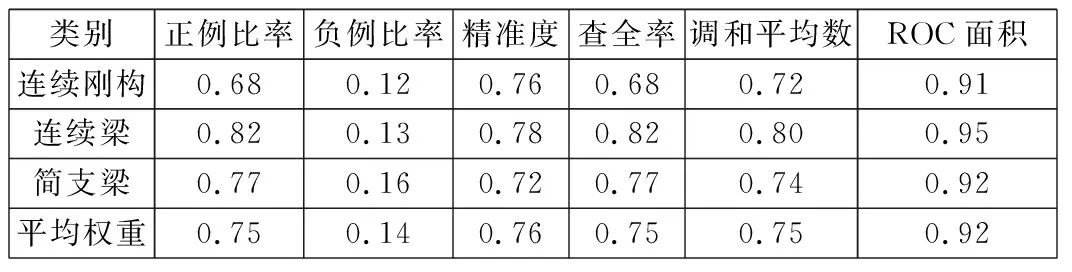
表2 朴素贝叶斯分类器详细精度

从表2～表4可知：对于正例比率平均权重，朴素贝叶斯>神经元网络>简单逻辑回归；对于负例比率平均权重，简单逻辑回归>神经元网络>朴素贝叶斯；对于精准度平均权重，朴素贝叶斯>神经元网络>简单逻辑回归；对于查全率平均权重，朴素贝叶斯>神经元网络>简单逻辑回归；对于调和平均数平均权重，朴素贝叶斯>神经元网络>简单逻辑回归；对于ROC面积平均权重，朴素贝叶斯>神经元网络>简单逻辑回归。总的来说，朴素贝叶斯分类器的识别效果好于神经元网络和简单逻辑回归。以每张图片为一个单元节点，3种算法的节点错误率比较如表5所示。

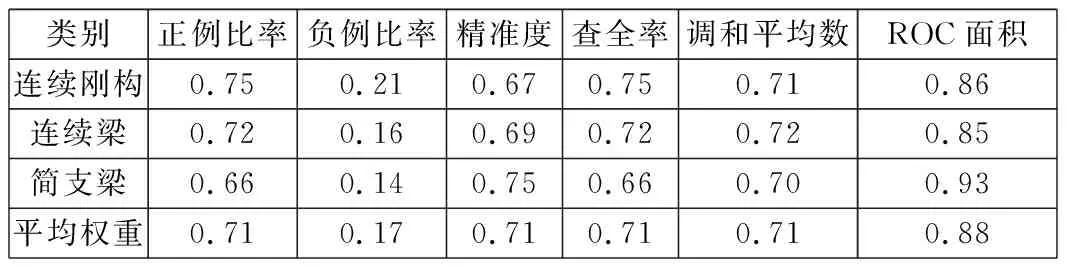
表3 神经元网络分类器详细精度

表4 简单逻辑回归详细精度

从表5可以看出：在平均绝对误差中，简单逻辑回归>神经元网络>朴素贝叶斯；在均方根误差中，神经元网络>简单逻辑回归>朴素贝叶斯；在相对绝对误差中，简单逻辑回归>神经元网络>朴素贝叶斯；在相对均方根误差中，神经元网络>简单逻辑回归>朴素贝叶斯。总体来说，朴素贝叶斯分类器的节点错误率明显低于其他两种分类器，可以得出朴素贝叶斯分类器在控制节点错误率方面优于其他两种分类器。

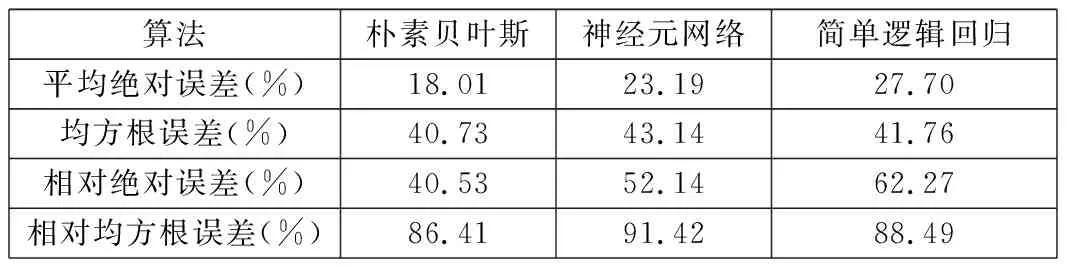
表5 节点错误率比较

三种分类器在连续刚构图片预测中都具有较好的效果，但朴素贝叶斯分类器和神经元网络分类器在简支梁图片识别中效果要优于简单逻辑分类器，并且3种分类器都会出现将连续梁识别为简支梁的情形。朴素贝叶斯分类器和神经元网络分类器能够准确识别桥梁变形和振动，但两种分类器都将其中4张连续梁图片预测为简支梁图片。简单逻辑分类器能够准确识别连续刚构桥梁状态，但对多张简支梁识别精度较差。

3 结语

以简支梁、连续梁、连续刚构3种类型桥梁图片数据作为样本，借助于数据挖掘与机器学习软件Weka和UltraEdit数据编辑软件，分别采用朴素贝叶斯、神经元网络、简单逻辑回归3种算法进行图片数据挖掘，建立训练模型。3种算法都能很好地实现训练集的训练和测试集的预测，预测结果准确率都在63%以上。朴素贝叶斯分类器和神经元网络分类器在准确度和详细精度上要略高于简单逻辑回归分类器。但在节点错误率上，朴素贝叶斯分类器要优于神经元网络分类器和简单逻辑回归分类器。朴素贝叶斯分类器和神经元网络分类器在预测准确度上要高于简单逻辑回归。总的来说，相比于其他两种分类器，朴素贝叶斯分类器的训练和预测效果是最好的。