基于改进梯度投影算法的移动机械臂轨迹规划研究
魏丽君 ,吴海波,刘海龙
(1.中南大学 信息科学与工程学院,湖南 长沙 410001;2.湖南铁道职业技术学院,湖南 株洲 412001)
随着应用领域的拓展,机械臂作业环境更为复杂,其运动时可能会与环境中的障碍物发生碰撞,导致任务无法完成,极大地制约了机械臂的应用。移动机械臂由移动平台和机械臂组成,通常具有冗余自由度。该特性使移动机械臂可以较好地解决上述问题[1-3]。冗余自由度机器人末端的某一特定位姿对应的机器人关节位形有无限多个,因此研究相应的轨迹规划问题是十分必要的。
许多学者对冗余自由度机器人的轨迹规划问题进行了深入研究。研究主要限定在固定环境下运动控制任务中,典型的研究结果包括面向笛卡尔空间或关节空间的多项式插值[4-7]、投影梯度法[8-10]、几何模型法[11-13]、人工势场法[14-16]、生物智能算法[17-19]等。近年来,一些研究开始将未知或动态环境的感知加入到轨迹规划的任务目标中,但这些成果往往也需要以上述研究成果作为基础,其中梯度投影法是提出较早、应用较广的一类方法[20-22]。
梯度投影法中的比例因子k的选择直接影响着目标函数优化效果。如果比例因子(绝对值)选择太小,关节空间自运动速度慢,运动优化效果不明显;如果比例因子选择太大,机器人关节空间自运动的速度可能很高而引起关节速度越限[23-27]。因此合理选择比例因子是梯度投影法中最为关键的一步。
目前关于选择比例因子的研究主要可以分为三类:① 取比例因子为常值,但这需要经过反复试值才能确定,应用烦琐;② 引入称为均衡比例因子的系数,保证特解和齐次解在一个数量级上,防止特解或齐次解被对方掩盖;③ 极值法:通过最优化方法求解,将比例因子作为目标函数,并结合一定的约束条件如关节速度极限、可优化度等。
极值法的应用较为广泛,其基本思想是找到比例因子的允许取值范围,然后取其为极值,以达到最速优化的目的;用这种方法取得的值能起到最速优化的效果,但由于缺少对机器人运动可优化能力的度量工具,常导致机器人关节角振荡。Xin等[5]提出了运动可优化度,建立了次最优化的放大系数,此种方法解决了放大系数的实时、连续、理想选取问题,使得关节速度具有较好的连续性,但没有讨论自运动限制因子的取值问题,从而忽略了任务时间段内各关节角速度的大小。杨三永等[8]讨论了自运动限制因子的取值,通过引入量化的优化力度函数用于单目标运动学优化控制,实现人为地控制任务时间段内关节角速度的大小。
笔者基于极值法求比例因子,引入可优化度和自运动限制因子来对其进行描述。在此基础上,针对极值法存在可能使关节加速度超限的问题,提出一种考虑关节加速度约束的新算法。
1 梯度投影法
一般地,机器人运动学方程可以表示为[28-29]
x=f(θ)
(1)
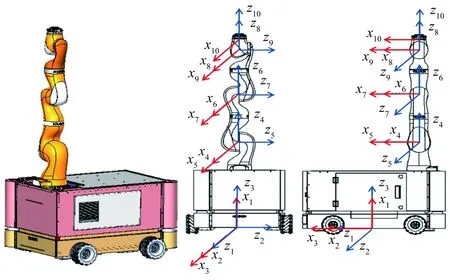
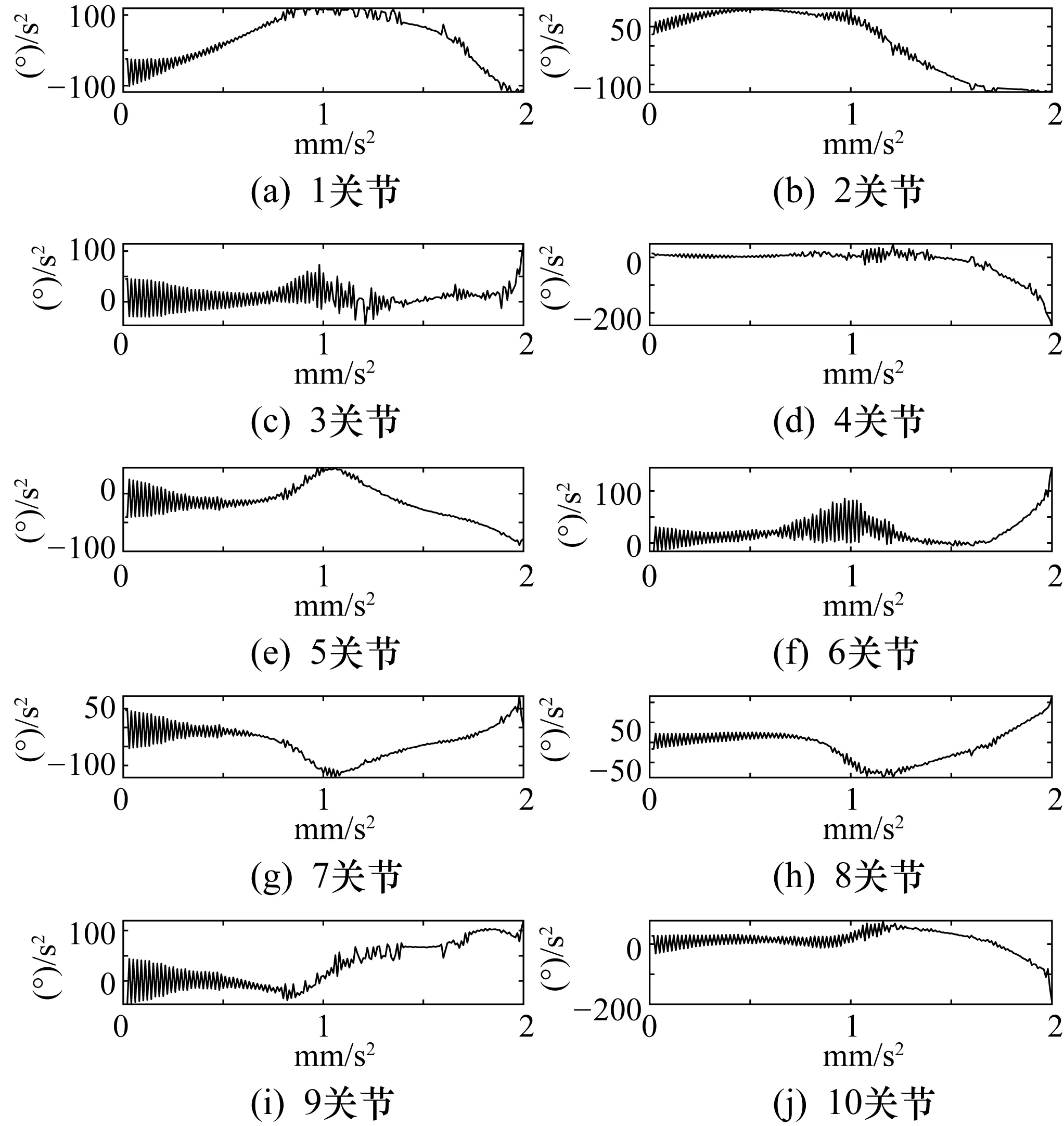
式中:x为机器人末端在笛卡儿空间的位姿,x∈Rm,对于平面问题m=3,空间问题m=6;θ为机器人关节空间的坐标,θ∈Rn,n为机器的关节数。当m (2) (3) 式中:J+为雅可比矩阵J的Moor-Penrose广义逆或伪逆。 (4) 把式(3)的齐次解引入到关节角速度解中,就得到了式(2)的通解。 (5) (6) 这是梯度投影法的基本公式。梯度投影法将逆运动学问题的解分解为最小范数解和齐次解两部分,即如式(6)所示。 基于速度约束的极值法求比例因子k值,并针对极值法未控制关节加速度的问题,引入关节加速度约束,介绍改进的考虑关节加速度的新方法。再介绍选取的优化准则,最后得到改进的梯度投影算法。 (1)比例因子。 使用传统的极值法求比例因子时,引入关节速度约束。 (7) (8) 那么,保证每个关节速度都不越限的比例因子k的极小值: kmin=max(k1min,k2min,…,kimin,…,knmin) (9) 但为弥补求解过程中加速度超限的缺陷,同时引入速度和加速度约束来选取k值。关节的速度约束同式(7)相同,引入关节加速度约束为 (10) 则由关节加速度约束,经过Δt时间后关节的速度约束为 (11) (12) (13) 与式(8)类似,由关节速度约束和加速度约束确定的比例因子极小值为 (14) (2)可优化度和自运动限制因子。 式(9)定义了保证速度约束条件下的比例因子k的选择,但还未定义k的使用条件,采用可优化度概念,性能指标对时间t的导数为 (15) 将式(6)代入得: (16) 因为I-J+J是一个幂等矩阵,所以: [▽H(θ)]T(I-J+J)·[▽H(θ)]>0 (17) 因此: (18) 定义可优化度λ为 (19) k值应取为可优化度λ的光滑连续函数: k=(1-e-βλ)kmin (20) 式中:β为自运动限制因子,将λ所表示的运动可优化能力转化为连续变换的k值。当λ较大时,k≈kmin,对应的自运动也较大,可实现最速优化;当λ较小时|k|<|kmin|,自运动相对减小。 假设允许最大自运动速度是极限值的90%,即k=0.9kmin,即: 1-e-βλm=0.9 (21) (22) 式中:λm为λ的局部极大值。因此由式(20)可知,k值应取为 (23) (3)机器人关节位移极限指标。 由于机器人关节的机械结构和内部走线的限制,机器人各关节不可能无限制的运动,因此,避免关节角越限是保证机器人安全运行的关键。可将关节许可位移的中值作为势力场的引力源,构建避关节极限位移指标。 (24) 式中:n为关节数目;θimin为负方向关节位移极限,同理,正方向关节位移极限为θimax;ai为θimax和θimin的中值,即ai=0.5(θimax+θimin)。由上述分析可得改进的梯度投影法公式为 (25) 根据前两节的讨论,当输入给定的笛卡尔空间轨迹后,经过上述算法,可以得到关节空间的轨迹,完成冗余机器人各关节的控制,实现关节空间的轨迹规划,其轨迹规划算法如表1所示。 表1 轨迹规划算法的伪代码 移动机械臂按照标准D-H方法建立坐标系如图1所示,按照右手定则确定Y轴。该机器人由3自由度的移动平台和7自由度的机械臂组成,移动平台由2个移动关节和1个转动关节组成,机械臂由7个转动关节组成。其参数如表2所示。 表2 机器人D-H参数表 图1 仿真移动机械臂构型和D-H坐标系 仿真研究的参数如下: (1)初始状态。 初始关节角:θ0=[100,100,30,30,30,30,30,30,30,30],移动关节单位为mm,转动关节单位为(°)。初始机器人末端姿态x0=[-362.12,-27.74,1374.06,41.614,-76.492,-68.522],末端位置的单位为mm,末端姿态的单位为(°)。限定关节的速率的最大值分别为[1000,1000,160,160,160,160,160,160,190,190],线性速度单位为mm/s,关节角加速度单位为(°/s2)。关节的加速度绝对值的最大值分别为[1200,1200,320,320,320,320,320,320,380,380],线性加速度单位为mm/s2,关节角加速度单位为(°/s2)。仿真步长为0.01 s,总时长2 s,共计200步。 (2)目标轨迹。 笛卡尔空间轨迹:末端位置的单位为mm,末端姿态的单位为(°),t为时间。由笛卡尔轨迹的末端位姿可得机器人末端相对于基坐标系的任务速度: (26) (27) 末端位置速度的单位为mm/s,末端姿态速度的单位为(°/s),t为时间。 仿真时间:2 s;采样周期:0.01 s。 (3)性能指标。 本文采用避关节位移极限准则(式(24))。 在本例中有: (28) 性能指标的梯度函数为 (29) 在此例中:λm=0.115。 在相同计算平台(CPU:Intel i7-8700 3.2 GHz,RAM:16 GB)进行仿真研究。通过比较加速度和轨迹规划计算时间评价相关算法。 4.2.1 考虑关节加速度约束算法的仿真结果 当加入本文所考虑的关节加速度约束,即采用式(14)计算比例因子,仿真计算历时 1.274461 s,机械臂轨迹如图2所示。 图2 考虑关节加速度约束算法的10自由度冗余机械臂运动轨迹图 由图2可知机械臂末端的轨迹符合要求。其各关节加速度变化情况如图3所示。 图3 考虑关节加速度约束算法的10关节加速度变化图 由图3可得,在此例中,10个关节的加速度绝对值最大值分别为:[35.3499,39.5947,210.2016,186.5748,156.5505,179.0516,247.9526,189.1394,152.4408,353.9720]。其中移动关节单位为mm/s2,转动关节单位为(°)/s2。各关节加速度均在加速度约束范围内。 4.2.2 考虑关节速度约束的对比算法的仿真结果 当采用速度约束的极值法,即采用式(8)计算比例因子,仿真计算历时 1.248230 s,机械臂的运动轨迹如图4所示。 图4 考虑关节速度约束的对比算法的10自由度冗余机械臂运动轨迹图 由图4可得,仿真过程中,机械臂末端轨迹符合要求。机械臂各关节的运动加速度如图5所示。 图5 考虑关节速度约束的对比算法的10关节加速度变化图 由图5可得,此时这10个关节的加速度绝对值最大值分别为:[206.94,1610.45,2860.14,1869.84,3285.68,5072.16,5134.45,975.01,2272.34,2872.00]。其中移动关节单位为mm/s2,转动关节单位为(°)/s2,远超过加速度限定范围。 4.2.3 考虑关节加速度约束的对比算法的仿真结果 为了与考虑关节加速度约束的典型算法进行比较,还针对文献[29]提出的算法进行了对比研究,该算法以时间冲击最优为目标进行轨迹规划,并采用模拟退火遗传算法求解,仿真计算历时 6.061188 s,机械臂的运动轨迹如图6所示。 图6 考虑关节加速度最优的对比算法的10自由度冗余机械臂运动轨迹图 由图6可知机械臂末端的轨迹符合要求。其各关节加速度变化情况如图7所示。 图7 考虑关节加速度最优的对比算法的10关节加速度变化图 由图7可得,在此例中10个关节的加速度绝对值最大值分别为:[118.80,119.21,114.40,245.46,89.22,144.81,132.11,115.78,119.63,190.11]。其中移动关节单位为mm/s2,转动关节单位为(°)/s2。各关节加速度均在加速度约束范围内,由于以时间冲击作为最优目标,该算法的关节加速度较本文提出的算法低,但该算法的时间复杂度相对较高。 在分析移动机械臂自由度高、稳定性差、在运动学及轨迹规划上存在问题的基础上,采用梯度投影法进行了逆运动学分析,梯度投影法将逆解分为最小范数解和零空间的齐次解两部分,采用极值法计算决定最小范数解和齐次解所占比例的比例因子。引入可优化度概念来定义比例因子的使用条件,引入自运动限制因子的概念保证比例因子的连续性。为弥补求解过程中关节加速度超限,在极值法求比例因子的过程中引入关节加速度约束,改进了梯度投影算法。介绍了冗余自由度机器人运动学性能优化指标。在求解逆解的过程中可完成机器人关节空间的轨迹规划,给出了逆解算法的伪代码。对逆解算法进行了仿真研究。在给出机械臂的初始状态、目标轨迹和性能指标后,对传统算法和改进后的算法进行了对比仿真,验证了所提算法控制关节加速度的有效性。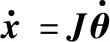


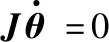
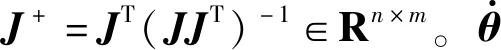
2 改进的梯度投影法

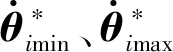

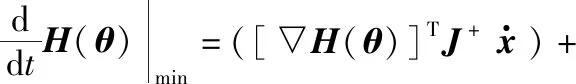


3 基于改进梯度投影法的轨迹规划算法

4 仿真研究
4.1 仿真研究环境



4.2 仿真结果





5 结束语

