基于分组选择的可调聚类网络中个体的合作行为研究
邓云生,张纪会
(青岛大学 a.复杂性科学研究所;b.山东省工业控制技术重点实验室,山东 青岛 266071)
0 引言
自然界和人类社会中的合作现象随处可见,然而其背后的形成原因却一直是未解之谜[1]。各领域的学者从自身专业的角度对此提出了不同且深刻的见解。在众多的研究中,值得一提的是Nowak和May[2]将复杂网络模型和博弈论模型相结合,通过计算机仿真来研究合作问题的形成原因。在他们的研究中用方格网来代表合作个体之间的物理连接,用弱囚徒博弈模型来描述个体之间通过互动而获得的收益状况,大量仿真结果表明,个体倾向于聚集在一起形成合作簇来抵抗背叛策略的入侵。受他们研究的启发,大量的研究工作使用这种跨学科相结合的方法,研究中使用的网络模型也不局限于方格网,进而拓展到BA无标度网络[3]、小世界网络[4]、关联网络[5],使用的博弈模型不仅有常见的囚徒博弈[6-8],还包括雪堆博弈[9-11]、猎鹿博弈[12-13]、公共品博弈[14-16]等。
BA网络一度被认为是对现实网络的真实描述,但随着研究的深入,却发现BA模型虽然能够描述现实网络的“无标度”特性,但却不能描述现实网络的“聚类”特性。为此,Holme等人[17]修改了BA网络的生成算法,最终生成同时具有“无标度”和“聚类可调”特性的网络。在此网络基础上,一些对演化合作行为的研究得以展开[18-20]。Assenza等人[18]发现,改进后的网络的高聚类特性有助于促进网络中个体合作行为的涌现。Rong等人[19]研究了可调聚类网络上的公共品博弈,发现网络中存在的三角结构反馈机制在促进合作中的关键作用。Wang等人[20]进一步改进了可调聚类网络,修改后的网络模型能够更准确地反映现实社会中的合作关系。
在上述研究的基础上,本文研究了可调聚类网络中囚徒博弈困境下的合作问题。通过引入一个可调节参数对博弈个体的邻居节点进行分组,并赋予博弈个体一定长度的记忆。个体通过对特定分组中的邻居的学习,最终可以提高网络的整体合作水平。
1 可调聚类网络与博弈个体互动规则
1.1 可调聚类网络
网络的平均聚类系数反映了网络中节点聚集的程度,其定义为
(1)


图1 可调聚类网络平均聚类系数变化Fig.1 Variation of average clustering coefficient of adjustable clustering networks
图1所示的网络初始时有2个相互连接的节点,网络中每加入一个新节点都会在网络中增加2个链接,直至达到网络规模N=5 000为止。在概率Pt从0增加到1的过程中,网络的度分布仍然服从幂律分布,但其平均聚类系数CC随Pt的增大而增大,故可以直接使用Pt值来代表不同平均聚类水平的网络。
1.2 个体互动规则
网络中持有合作策略(Cooperation,C)的节点称为合作者(cooperator),持有背叛策略(Defection,D)的节点称为背叛者(defector)。持有不同策略的节点互动时根据囚徒博弈(Prisoner′s Dilemma Game,PDG)所描述的收益矩阵获得相应的收益。本文使用文献[2]所描述的弱囚徒博弈收益矩阵:
CD

(2)
当两个合作者互动时,每位合作者获得收益R=1;两个背叛者互动时,每位背叛者获得收益P=0;当合作者与背叛者互动时,合作者获得收益S=0,背叛者获得收益T=b;其中b>1。
在传统的网络节点博弈过程中,每一个节点在修改自己的策略之前,通常要选择一个学习的目标,然后再通过一定的概率(例如费米函数、比例函数等)来判断是否学习该目标的策略。节点通常采用随机挑选的方式从自己的邻居中选择学习目标,这种方式虽然简单,但却忽略了个体在选择过程中的主观能动性。现实中个体在挑选学习目标时往往带有特定的指向,而非无目的地随机挑选,被选中的学习目标往往具有能够满足挑选者需要的某种特质。基于以上观察,提出一种分组选择的方法进行学习目标的选择。
假设网络中每一个节点能够记忆M轮博弈过程中所使用的策略和获得的收益,则对于网络中度值为k的节点x,在M轮博弈过程中每一份链接给节点x带来的平均收益定义为
(3)
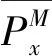

(4)
其中,κ=0.1代表系统的噪声和不确定性。一旦i确定向节点j学习,节点i可直接模仿节点j在最近一轮博弈中所使用的策略[11-15],或综合考虑各种因素(例如:记忆、情绪、收益等等)做出策略选择[7,21-22]。我们并不使用直接模仿的策略,而是综合考虑节点j在过去M轮博弈中所使用的策略和收益而做出决策。节点i所采取的策略S定义为
(5)
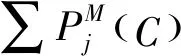
2 仿真分析
2.1 预期最小收益对可调聚类网络中合作行为的影响
所有仿真实验中,网络规模N=5 000,初始时刻合作策略与背叛策略以相同的数量随机均匀分布在网络中,即此时合作密度fc=0.5。每一次实验都进行10 000步仿真,同时为了避免随机性带来的影响,仿真图中所呈现的每一组数据都是50次独立实验后取平均值的结果。
首先考查用于分组的参数emp对可调聚类网络中节点合作行为的影响,仿真结果如图2所示。

图2 emp对不同聚类水平网络合作密度的影响Fig.2 The effect of emp on the cooperation densities of networks with different clustering levels
图2所示实验在M=7,b=1.1的4组不同聚类水平的网络上进行,其中参数emp从0.3变化到1.2。由图2可看出,不同聚类水平的网络的合作密度fc随着参数emp的增大呈现出相似的变化规律。以Pt=0.6为例,当emp在区间[0.3,0.6]内单调递增时,fc随之单调递增,一旦emp值超过0.6,其对应的fc急剧下降到低于初始合作值0.5的程度。随着emp的继续增大,fc的值有所上升,但仍然低于初始值0.5,最终当emp≥1.1时,fc等于初始值0.5。究其原因,可以发现随着emp的增加,高收益群组的范围在不断缩小,即|Ω|的值随emp增加而减小,因为在囚徒博弈中相比于合作策略,背叛策略能带来更大的收益(T>R),当emp低于0.6时挑选到因合作策略而得到高收益的节点的可能性较大,当emp高于0.6时,高收益组中的节点很可能都是因背叛策略而获得高收益,此时从中挑选学习目标并向其学习,往往学习的是背叛策略,从而导致整体合作率下降。随着emp不断增大,|Ω|不断变小,直至emp≥1.1时,|Ω|=0,此时高收益组中没有任何节点,因此,也不会有节点被选为学习目标,按照节点的互动规则,此时,网络中的每一个节点保持初始策略不变,故整体的合作密度fc也维持在初始状态0.5不发生变化。
当emp处于促进合作行为的区间[0.3,0.6]内时,不同聚类水平的网络最终的合作者密度fc也是不相同的。在相同的emp下,聚类水平高(Pt值大)的网络中的合作者密度要高于聚类水平低(Pt值小)的网络中的合作者密度,充分体现了无标度网络的高聚类特性对群体合作行为的促进作用。而在emp>0.6时,不同聚类水平的网络其合作者密度都是大幅度下降的,而且此时在相同的emp下,不同网络的合作密度在数值上非常接近并无明显差异,这说明此时无标度网络的高聚类特性并没有发挥对合作行为的促进作用,这与以往研究的结论[18]是不同的。
2.2 个体记忆长度与聚类性对网络中合作行为的影响
由个体的互动规则可知,参数emp和M共同对合作密度产生影响,接下来固定emp的值,考察另一个重要参数M对群体合作行为的影响。令emp=0.5,b=1.1,不同聚类水平网络上的仿真结果如图3所示。
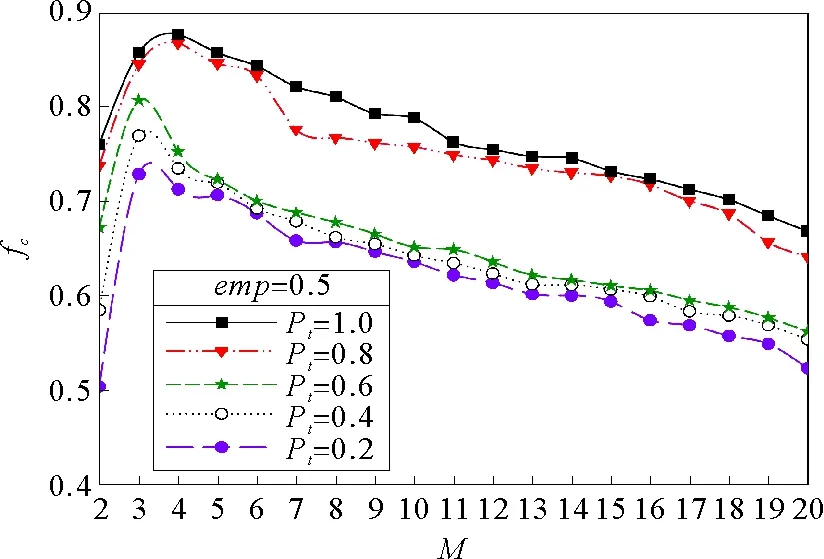
图3 记忆长度对不同聚类水平网络合作密度的影响Fig.3 The effect of memory length on the cooperation densities of networks with different clustering levels
图3中,emp=0.5处于促进合作行为的区间[0.3,0.6],个体记忆长度M从2变化到20。在不同聚类水平的网络中,合作密度随着M增加呈现出相似的演化规律:从低到高然后再转低,这也意味着个体的记忆长度的增加对合作行为的影响先是促进然后转为抑制。这种先促进后抑制的演化规律说明,在给定的条件下,存在一个与M相关的点或区间,当M在该点取值或该区间内取值时,其所在网络的合作密度将达到最大值。由图3可以发现:当Pt=0.2,0.4,0.6时,M=3可以使对应的网络合作密度达到最大值;而当Pt=0.8,1.0时,M=4可以使对应的网络合作密度达到最大值。从图3还可以发现:在不同聚类水平的网络上,短期记忆(3≤M≤6)比长期记忆更有利于合作密度的提高。
此外,网络的高聚类特性对合作行为的促进作用也可以从图3中观察到。对于相同的M,聚类水平高的网络对应的合作密度高于聚类水平低的网络所对应的合作密度,这是因为在高聚类的网络中会存在一种具有极高连接度的节点(也称为hub节点),而这些hub节点会因为累积收益的计算方式而倾向于采用合作策略[18]。一旦这些hub节点成为合作者,因为与其连接的节点众多,这些节点必然受到hub节点的影响而模仿其合作策略,最终会导致大量合作策略在网络中传播。图4进一步展示了高聚类特性对hub节点策略行为的影响。
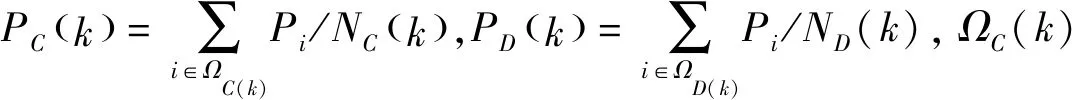
由图4可以看出,不同聚类水平的网络中,k值较小(k<18)的节点中合作者与背叛者并存,而k值较大(k>70)的hub节点中只有合作者的存在,进一步说明hub节点往往采用合作策略,成为合作者。在同一聚类水平的网络中,这种“合作者高收益”的hub节点又会对周围大量围绕的相邻节点产生一种榜样示范效应,促使其模仿hub节点的合作策略以争取获得高收益。这些hub节点的度值越大,影响到的相邻节点也越多,其榜样示范效应也越强,一旦其相邻节点转变为合作者,又能给与它相连的hub节点提供更多的收益。hub节点与其相邻节点之间形成一种正向反馈的互动模式,所以,这些hub节点的收益整体呈现出一种随连接度增大而增加的趋势(见图4b或4d)。
这种hub节点与网络生成算法中的参数Pt有关,Pt值越大会导致其生成的网络中高连接度的hub节点的度值越大,例如图4b中,Pt=0.2时生成的网络中最大度值的hub节点度为153,收益为131,而在图4d中,Pt=0.7时生成的网络中最大度值的hub节点度值为162,收益为139。此外,Pt值的大小也代表着网络的聚类水平的高低。由上述分析可知,网络的聚类性越高对合作行为的促进作用也越大。

图4 连接度为k的节点数量及其收益Fig.4 The number of nodes with connection degree k and their payoffs
2.3 互动规则的应用扩展
以上研究中,我们将个体互动规则应用在聚类可调网络中,探讨了参数emp和M对高聚类网络中合作行为的影响。本节,我们改变底层的网络结构,将个体的互动规则应用在方格网和小世界网络上,探讨其合作行为演化过程,仿真结果如图5所示。

图5 emp对方格网和小世界网中合作行为的影响Fig.5 The impact of emp on cooperative behavior in Lattice and small-world networks
图5a所示的仿真实验是在规模为N=50×50的方格网上进行的,图5b是在规模为N=2 500的小世界网络[4]上进行的,小世界网络中节点间的重连概率为0.01。个体互动过程中使用公式(2)所示的弱囚徒博弈,b=1.1,博弈个体的记忆长度M=10,每次实验过程经历了10 000步仿真,每组数据是50次独立实验后取平均值的结果。为清晰展示合作率的演化过程,图5中的横坐标为对数坐标。

3 结论
论文研究了网络的聚类性(Pt)、用于分组的最小期望收益值(emp)和博弈个体的记忆长度(M)三者对网络合作行为的影响。研究发现,存在一个与emp相关的区间(例如,0.3≤emp≤0.5,见图2),在此区间内emp与Pt具有促进合作策略传播的作用。同时,较小的记忆长度M(例如,2≤M≤6,见图3)有利于促进合作行为的形成。这些结果说明对于一个给定的聚类可调网络,只需要指定emp与M的值,就可以使合作策略在网络中传播的效率达最大化,为我们促进网络中合作行为的传播提供了一种新方法。

